3.4E: Ejercicios para la Sección 3.4
- Page ID
- 116665
En los ejercicios 1 - 3, las funciones dadas representan la posición de una partícula viajando a lo largo de una línea horizontal.
a. Encuentra las funciones de velocidad y aceleración.
b. Determinar los intervalos de tiempo cuando el objeto se está ralentizando o acelerando.
1)\(s(t)=2t^3−3t^2−12t+8\)
2)\(s(t)=2t^3−15t^2+36t−10\)
- Contestar
- a.\(v(t)=6t^2−30t+36,\quad a(t)=12t−30\);
b. acelera para\( (2,2.5)∪(3,∞)\), ralentiza para\((0,2)∪(2.5,3)\)
3)\(s(t)=\dfrac{t}{1+t^2}\)
4) Un cohete es disparado verticalmente hacia arriba desde el suelo. La distancia\(s\) en pies que el cohete recorre desde el suelo después de\(t\) segundos viene dada por\(s(t)=−16t^2+560t\).
a. Encuentra la velocidad del cohete 3 segundos después de haber sido disparado.
b. Encuentra la aceleración del cohete 3 segundos después de haber sido disparado.
- Contestar
- a.\(464\; \text{ft/s}^2\)
b.\(−32\;\text{ft/s}^2\)
5) Se lanza una pelota hacia abajo con una velocidad de 8 pies/s desde lo alto de un edificio de 64 pies de altura. Después de\(t\) segundos, su altura sobre el suelo viene dada por\(s(t)=−16t^2−8t+64.\)
a. Determinar cuánto tiempo tarda la pelota en golpear el suelo.
b. Determinar la velocidad de la pelota cuando golpea el suelo.
6) La función de posición\(s(t)=t^2−3t−4\) representa la posición de la parte trasera de un automóvil retrocediendo de un camino de entrada y luego conduciendo en línea recta, donde\(s\) está en pies y\(t\) está en segundos. En este caso,\(s(t)=0\) representa la hora en la que la parte trasera del auto está en la puerta del garaje, así\(s(0)=−4\) es la posición inicial del auto, 4 pies dentro de la cochera.
a. Determinar la velocidad del carro cuando\(s(t)=0\).
b. Determinar la velocidad del carro cuando\(s(t)=14\).
- Contestar
- a.\(5\) pies/s
b.\(9\) pies/s
7) La posición de un colibrí volando en línea recta en\(t\) segundos viene dada por\(s(t)=3t^3−7t\) metros.
a. Determinar la velocidad del ave a la\(t=1\) sec.
b. Determinar la aceleración del ave a la\(t=1\) sec.
c. Determinar la aceleración del ave cuando la velocidad sea igual a 0.
8) Una papa se lanza verticalmente hacia arriba con una velocidad inicial de 100 pies/s desde una pistola de papa en la parte superior de un edificio de 85 pies de altura. La distancia en pies que la papa recorre desde el suelo después de\(t\) segundos viene dada por\(s(t)=−16t^2+100t+85\).
a. Encontrar la velocidad de la papa después de\(0.5\)\(5.75\) s y s.
b. encontrar la velocidad de la papa en\(0.5\)\(5.75\) s y s.
c. Determinar cuándo la papa alcanza su altura máxima.
d. Encuentra la aceleración de la papa en\(0.5\)\(1.5\) s y s.
e. Determinar cuánto tiempo está la papa en el aire.
f. Determinar la velocidad de la papa al golpear el suelo.
- Contestar
- a. 84 pies/s, −84 pies/s
b. 84 pies/s
c.\(\frac{25}{8}\) s.
d.\(−32 \; \text{ft/s}^2\) en ambos casos
e.\(\frac{1}{8}(25+\sqrt{965})\) s.
f.\(−4\sqrt{965}\) pies/s
9) La función de posición\(s(t)=t^3−8t\) da la posición en millas de un tren de carga donde el este es la dirección positiva y\(t\) se mide en horas.
a. Determinar la dirección en la que viaja el tren cuando\(s(t)=0\).
b. Determinar la dirección en la que viaja el tren cuando\(a(t)=0\).
c. Determinar los intervalos de tiempo cuando el tren está desacelerando o acelerando.
10) La siguiente gráfica muestra la posición\(y=s(t)\) de un objeto moviéndose a lo largo de una línea recta.
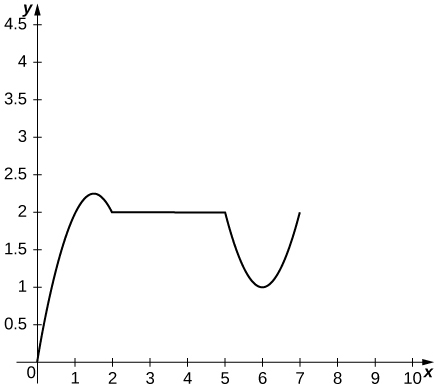
a. Utilice la gráfica de la función de posición para determinar los intervalos de tiempo cuando la velocidad es positiva, negativa o cero.
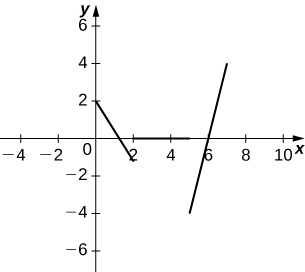
b. Esbozar el gráfico de la función de velocidad.
c. Utilice la gráfica de la función de velocidad para determinar los intervalos de tiempo cuando la aceleración es positiva, negativa o cero.
d. Determinar los intervalos de tiempo cuando el objeto se está acelerando o desacelerando.
- Contestar
- a. La velocidad es positiva activa\((0,1.5)∪(6,7)\)\((1.5,2)∪(5,6)\), negativa y cero activa\((2,5)\).
b.
c. La aceleración es positiva\((5,7)\) activa, negativa y cero activa\((2,5)\).\((0,2)\)
d. El objeto se está acelerando\((6,7)∪(1.5,2)\) y desacelerando\((0,1.5)∪(5,6)\).
11) La función de costo, en dólares, de una empresa que fabrica procesadores de alimentos viene dada por\(C(x)=200+\dfrac{7}{x}+\dfrac{x}{27}\), donde\(x\) está el número de procesadores de alimentos fabricados.
a. Encontrar la función de costo marginal.
b. Encontrar el costo marginal de fabricar 12 procesadores de alimentos.
c. Encontrar el costo real de fabricar el decimotercer procesador de alimentos.
12) El precio p (en dólares) y la\(x\) demanda de cierto radio reloj digital viene dado por la función precio-demanda\(p=10−0.001x\).
a. Encontrar la función de ingresos\(R(x)\)
b. Encontrar la función de ingresos marginales.
c. Encontrar los ingresos marginales en\(x=2000\) y\(5000\).
- Contestar
- a.\(R(x)=10x−0.001x^2\)
b.\( R′(x)=10−0.002x\)
c. $6 por artículo, $0 por artículo
13) [T] Se obtiene una ganancia cuando los ingresos superan el costo. Supongamos que la función de beneficio para un fabricante de monopatines viene dada por\(P(x)=30x−0.3x^2−250\), donde\(x\) esta el numero de patinetas vendidas.
a. Encuentra el beneficio exacto de la venta del trigésimo monopatín.
b. Encontrar la función de beneficio marginal y utilizarla para estimar el beneficio de la venta del trigésimo monopatín.
14) [T] En general, la función de ganancia es la diferencia entre las funciones de ingreso y costo:\(P(x)=R(x)−C(x)\).
Supongamos que las funciones precio-demanda y costo para la producción de taladros inalámbricos están dadas respectivamente por\(p=143−0.03x\) y\(C(x)=75,000+65x\), donde\(x\) está el número de taladros inalámbricos que se venden a un precio de\(p\) dólares por taladro y\(C(x)\) es el costo de producir taladros\(x\) inalámbricos.
a. Encontrar la función de costo marginal.
b. Encontrar las funciones de ingresos e ingresos marginales.
c. Encontrar\(R′(1000)\) y\(R′(4000)\). Interpretar los resultados.
d. Encontrar las funciones de ganancia y beneficio marginal.
e. encontrar\(P′(1000)\) y\(P′(4000)\). Interpretar los resultados.
- Contestar
- a.\(C′(x)=65\)
b.\(R(x)=143x−0.03x^2\),\(R′(x)=143−0.06x\)
c.\(R′(1000)=83, \quad R′(4000) = −97\) A un nivel de producción de 1000 taladros inalámbricos, los ingresos están aumentando a una tasa de 83 dólares por taladro; a un nivel de producción de 4000 taladros inalámbricos, los ingresos están disminuyendo a una tasa de $97 por taladro.
d.\(P(x)=−0.03x^2+78x−75000, \quad P′(x)=−0.06x+78\)
e\(P′(1000)=18, \quad P′(4000) =−162\). A un nivel de producción de 1000 taladros inalámbricos, las ganancias están aumentando a una tasa de $18 por taladro; a un nivel de producción de 4000 taladros inalámbricos, la ganancia está disminuyendo a una tasa de $162 por taladro.
15) Un pequeño pueblo de Ohio encargó a una firma actuarial que realizara un estudio que modelara la tasa de cambio de la población del pueblo. El estudio encontró que la población del pueblo (medida en miles de personas) puede ser modelada por la función\(P(t)=−\frac{1}{3}t^3+64t+3000\), donde\(t\) se mide en años.
a. Encontrar la función de tasa de cambio\(P′(t)\) de la función de población.
b. Encontrar\(P′(1),\; P′(2),\; P′(3)\), y\(P′(4)\). Interpretar lo que significan los resultados para el pueblo.
c. Encontrar\(P''(1),\; P''(2),\; P''(3)\), y\(P''(4)\). Interpretar lo que significan los resultados para la población del pueblo.
16) [T] Un cultivo de bacterias crece en número según la función\(N(t)=3000(1+\dfrac{4t}{t^2+100})\), donde\(t\) se mide en horas.
a. Encontrar la tasa de cambio del número de bacterias.
b. Encontrar\(N′(0),\; N′(10),\; N′(20)\), y\(N′(30)\).
c. Interpretar los resultados en (b).
d. encontrar\(N''(0),\; N''(10),\; N''(20),\) y\(N''(30)\). Interpretar lo que implican las respuestas sobre el crecimiento de la población bacteriana.
- Contestar
- a.\(N′(t)=3000\left(\dfrac{−4t^2+400}{(t^2+100)^2}\right)\)
b.\(120,0,−14.4,−9.6\)
c. La población de bacterias aumenta de 0 a 10 horas; posteriormente, la población de bacterias disminuye.
d\(0,−6,0.384,0.432\). La velocidad a la que aumenta la bacteria está disminuyendo durante las primeras 10 horas. Posteriormente, la población de bacterias está disminuyendo a un ritmo decreciente.
17) La fuerza centrípeta de un objeto de masa m viene dada por\(F(r)=\dfrac{mv^2}{r}\), donde\(v\) está la velocidad de rotación y\(r\) es la distancia desde el centro de rotación.
a. Encontrar la tasa de cambio de la fuerza centrípeta con respecto a la distancia desde el centro de rotación.
b. encontrar la tasa de cambio de la fuerza centrípeta de un objeto con masa 1000 kilogramos, velocidad de 13.89 m/s, y una distancia desde el centro de rotación de 200 metros.
Las siguientes preguntas se refieren a la población (en millones) de Londres por década en el siglo XIX, que se enumera en la siguiente tabla.
| Año Desde 1800 | Población (millones) |
| 1 | 0.8975 |
| 11 | 1.040 |
| 21 | 1.264 |
| 31 | 1.516 |
| 41 | 1.661 |
| 51 | 2.000 |
| 61 | 2.634 |
| 71 | 3.272 |
| 81 | 3.911 |
| 91 | 4.422 |
Población de LondresFuente: http://en.Wikipedia.org/wiki/Demographics_of_London
18) [T]
a. Usando una calculadora o un programa de computadora, encuentre la función lineal que mejor se ajuste para medir la población.
b. Encontrar la derivada de la ecuación en a. y explicar su significado físico.
c. Encontrar la segunda derivada de la ecuación y explicar su significado físico.
- Contestar
- a.\(P(t)=0.03983+0.4280\)
b\(P′(t)=0.03983\). La población va en aumento.
\(P''(t)=0\)c. La tasa a la que aumenta la población es constante.
19) [T]
a. Usando una calculadora o un programa de computadora, encuentre la curva cuadrática que mejor se ajuste a través de los datos.
b. Encontrar la derivada de la ecuación y explicar su significado físico.
c. Encontrar la segunda derivada de la ecuación y explicar su significado físico.
Para los siguientes ejercicios, considera a un astronauta en un gran planeta en otra galaxia. Para conocer más sobre la composición de este planeta, el astronauta deja caer un sensor electrónico en una zanja profunda. El sensor transmite su posición vertical cada segundo en relación con la posición del astronauta. El resumen de los datos del sensor de caída se muestra en la siguiente tabla.
| Tiempo después de la caída (s) | Posición (m) |
| 0 | 0 |
| 1 | −1 |
| 2 | −2 |
| 3 | −5 |
| 4 | −7 |
| 5 | −14 |
20) [T]
a. Usando una calculadora o programa de computadora, encuentre la curva cuadrática que mejor se ajuste a los datos.
b. Encontrar la derivada de la función position y explicar su significado físico.
c. Encontrar la segunda derivada de la función position y explicar su significado físico.
- Contestar
- a.\(p(t)=−0.6071x^2+0.4357x−0.3571\)
b\(p′(t)=−1.214x+0.4357\). Esta es la velocidad del sensor.
\(p''(t)=−1.214\)c. Esta es la aceleración del sensor; es una aceleración constante hacia abajo.
21) [T]
a. Usando una calculadora o programa de computadora, encuentre la curva cúbica que mejor se ajuste a los datos.
b. Encontrar la derivada de la función position y explicar su significado físico.
c. Encontrar la segunda derivada de la función position y explicar su significado físico.
d. Usando el resultado de c. explicar por qué una función cúbica no es una buena opción para este problema.
Los siguientes problemas tratan con las ecuaciones Holling tipo I, II y III. Estas ecuaciones describen el evento ecológico de crecimiento de una población depredadora dada la cantidad de presas disponibles para el consumo.
22) [T] La ecuación de Holling tipo I se describe por\(f(x)=ax\), donde\(x\) está la cantidad de presas disponibles y\(a>0\) es la velocidad a la que el depredador se encuentra con la presa para su consumo.
a. Grafique la ecuación Holling tipo I, dada\(a=0.5\).
b. Determinar la primera derivada de la ecuación Holling tipo I y explicar físicamente lo que implica la derivada.
c. Determinar la segunda derivada de la ecuación Holling tipo I y explicar físicamente lo que implica la derivada.
d. Utilizando las interpretaciones de b. y c. explicar por qué la ecuación de Holling tipo I puede no ser realista.
- Contestar
-
a.
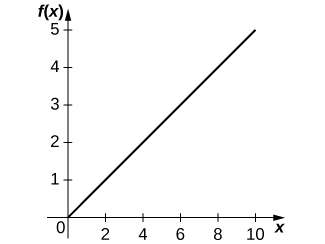
b\(f′(x)=a\). Cuanto mayor sea el aumento de las presas, mayor será el crecimiento de los depredadores.
\(f''(x)=0\)c. A medida que aumenta la cantidad de presas, la tasa a la que aumenta el crecimiento de la población depredadora es constante.
d. Esta ecuación supone que si hay más presas, el depredador es capaz de incrementar el consumo linealmente. Esta suposición es poco física porque esperaríamos que hubiera algún punto de saturación en el que haya demasiada presa para que el depredador la consuma adecuadamente.
23) [T] La ecuación de Holling tipo II se describe por\(f(x)=\dfrac{ax}{n+x}\), donde\(x\) está la cantidad de presas disponibles y\(a>0\) es la tasa máxima de consumo del depredador.
a. Grafique la ecuación Holling tipo II dada\(a=0.5\) y\(n=5\). ¿Cuáles son las diferencias entre las ecuaciones Holling tipo I y II?
b. Tomar la primera derivada de la ecuación de Holling tipo II e interpretar el significado físico de la derivada.
c. Demostrarlo\(f(n)=\frac{1}{2}a\) e interpretar el significado del parámetro n.
d. Encontrar e interpretar el significado de la segunda derivada. ¿Qué hace que la función Holling tipo II sea más realista que la función Holling tipo I?
24) [T] La ecuación de Holling tipo III se describe por\(f(x)=\dfrac{ax^2}{n^2+x^2}\), donde x es la cantidad de presas disponibles y\(a>0\) es la tasa máxima de consumo del depredador.
a. Grafique la ecuación Holling tipo III dada\(a=0.5\) y\(n=5.\) ¿Cuáles son las diferencias entre las ecuaciones Holling tipo II y III?
b. Tomar la primera derivada de la ecuación de Holling tipo III e interpretar el significado físico de la derivada.
c. Encontrar e interpretar el significado de la segunda derivada (puede ayudar a graficar la segunda derivada).
d. ¿Qué fenómenos ecológicos adicionales describe la función Holling tipo III en comparación con la función Holling tipo II?
- Contestar
-
a.
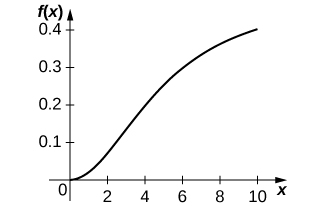
b\(f′(x)=\dfrac{2axn^2}{(n^2+x^2)^2}\). Cuando aumenta la cantidad de presas, aumenta el crecimiento del depredador.
\(f''(x)=\dfrac{2an^2(n^2−3x^2)}{(n^2+x^2)^3}\)c. Cuando la cantidad de presas es extremadamente pequeña, la tasa a la que aumenta el crecimiento de los depredadores está aumentando, pero cuando la cantidad de presas alcanza por encima de cierto umbral, la velocidad a la que aumenta el crecimiento de los depredadores comienza a disminuir.
d. En niveles más bajos de presa, la presa es más fácil de evitar la detección por parte del depredador, por lo que se consumen menos individuos presa, lo que resulta en un menor crecimiento de depredadores.
25) [T] Las poblaciones de la liebre raqueta de nieve (en miles) y el lince (en cientos) recolectadas a lo largo de 7 años de 1937 a 1943 se muestran en la siguiente tabla. La liebre raqueta de nieve es la principal presa del lince.
| Población de liebre raqueta (miles) | Población de lince (cientos) |
| 20 | 10 |
| 5 | 15 |
| 65 | 55 |
| 95 | 60 |
Poblaciones de liebre y lince con raquetas de nieveFuente: http://www.biotopics.co.uk/newgcse/predatorprey.html.
a. Grafique los puntos de datos y determine qué función de tipo Holling se ajusta mejor a los datos.
b. Utilizando los significados de los parámetros\(a\) y\(n\), determinar los valores para esos parámetros mediante el examen de una gráfica de los datos. Recordemos que\(n\) mide qué valor de presa da como resultado la mitad máxima del valor del depredador.
c. Trazar las funciones resultantes de tipo Holling I, II y III encima de los datos. ¿Fue correcto el resultado de la parte a.?

