3.5: Derivadas de Funciones Trigonométricas
- Page ID
- 116601
- Encuentra las derivadas de la función sinusoidal y coseno.
- Encuentra las derivadas de las funciones trigonométricas estándar.
- Calcular las derivadas de orden superior del seno y el coseno.
Uno de los tipos de movimiento más importantes en la física es el movimiento armónico simple, el cual se asocia con sistemas como un objeto con masa oscilante en un resorte. El movimiento armónico simple se puede describir mediante el uso de funciones sinusoidales o cosenales. En esta sección ampliamos nuestro conocimiento de fórmulas derivadas para incluir derivadas de estas y otras funciones trigonométricas. Comenzamos con las derivadas de las funciones seno y coseno y luego las usamos para obtener fórmulas para las derivadas de las cuatro funciones trigonométricas restantes. Poder calcular las derivadas de las funciones seno y coseno nos permitirá encontrar la velocidad y aceleración del movimiento armónico simple.
Derivadas de las funciones de seno y coseno
Comenzamos nuestra exploración de la derivada para la función sinusoidal usando la fórmula para hacer una suposición razonable sobre su derivada. Recordemos que para una función\(f(x),\)
\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
En consecuencia, para valores\(h\) muy cercanos a\(0\),
\[f′(x)≈\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Vemos que al usar\(h=0.01\),
\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
Por ajuste
\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
y usando una utilidad gráfica, podemos obtener una gráfica de una aproximación a la derivada de\(\sin x\) (Figura\(\PageIndex{1}\)).
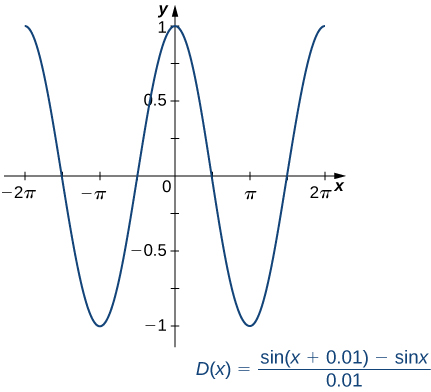
Tras la inspección, la gráfica de\(D(x)\) parece estar muy cerca de la gráfica de la función coseno. En efecto, vamos a demostrar que
\[\dfrac{d}{dx}(\sin x)=\cos x. \nonumber \]
Si tuviéramos que seguir los mismos pasos para aproximar la derivada de la función coseno, encontraríamos que
\[\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber \]
La derivada de la función sinusoidal es el coseno y la derivada de la función coseno es el seno negativo.
\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]
\[\dfrac{d}{dx}(\cos x)=−\sin x \nonumber \]
Debido a que las pruebas para\(\dfrac{d}{dx}(\sin x)=\cos x\) y\(\dfrac{d}{dx}(\cos x)=−\sin x\) utilizan técnicas similares, proporcionamos solo la prueba para\(\dfrac{d}{dx}(\sin x)=\cos x\). Antes de comenzar, recordamos dos importantes límites trigonométricos:
\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\)y\(\displaystyle \lim_{h→0}\dfrac{\cos h−1}{h}=0\).
Las gráficas de\(y=\dfrac{\sin h}{h}\) y\(y=\dfrac{\cos h−1}{h}\) se muestran en la Figura\(\PageIndex{2}\).
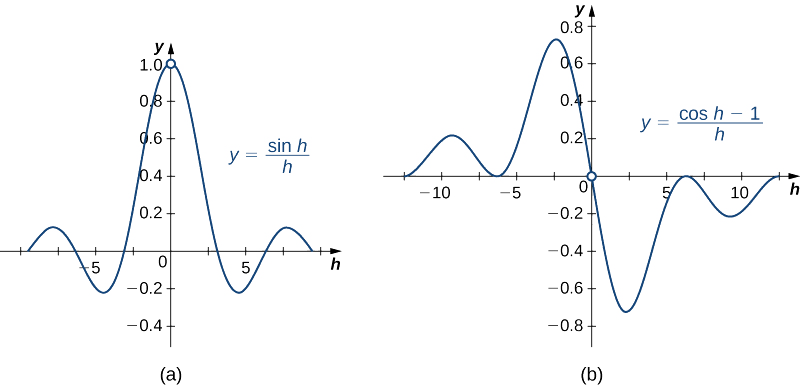
También recordamos la siguiente identidad trigonométrica para el seno de la suma de dos ángulos:
\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]
Ahora que hemos reunido todas las ecuaciones e identidades necesarias, procedemos con la prueba.
\ [\ begin {align*}\ dfrac {d} {dx} (\ sin x) &=\ lim_ {h→0}\ dfrac {\ sin (x+h) −\ sin x} {h} &\ text {Aplica la definición de la derivada.}\\ [4pt]
&=\ lim_ {h→0}\ dfrac {\ sin x\ cos h+\ cos x\ sin h−\ sin x} {h} &\ text {Usa la identidad trigonométrica para el seno de la suma de dos ángulos.}\\ [4pt]
&=\ lim_ {h→0}\ izquierda (\ dfrac {\ sin x\ cos h−\ sin x} {h} +\ dfrac {\ cos x\ sin h} {h}\ derecha) &\ text {Reagruparse.}\\ [4pt]
&=\ lim_ {h→0}\ izquierda (\ sin x\ izquierda (\ dfrac {cos\ h−1} {h}\ derecha) + (\ cos x)\ izquierda (\ dfrac {\ sin h} {h}\ derecha)\ derecha) &\ text {Factor de salida}\ sin x\ texto {y}\ cos x\\ [4pt]
& =(\ sin x)\ lim_ {h→0}\ izquierda (\ dfrac {\ cos h−1} {h}\ derecha) + (\ cos x)\ lim_ {h→0}\ izquierda (\ dfrac {\ sin h} {h}\ derecha) &\ text {Factor}\ sin x\ texto {y}\ cos x\ texto {fuera de límites.}\\ [4pt]
& =(\ sin x) (0) + (\ cos x) (1) & &\ text {Aplicar fórmulas de límite trigonométrico.}\\ [4pt]
&=\ cos x & &\ text {Simplificar.} \ end {align*}\ nonumber\]
□
La figura\(\PageIndex{3}\) muestra la relación entre la gráfica de\(f(x)=\sin x\) y su derivada\(f′(x)=\cos x\). Observe que en los puntos donde\(f(x)=\sin x\) tiene una tangente horizontal, su derivada\(f′(x)=\cos x\) adquiere el valor cero. También vemos que donde f\((x)=\sin x\) va en aumento,\(f′(x)=\cos x>0\) y donde\(f(x)=\sin x\) va disminuyendo,\(f′(x)=\cos x<0.\)
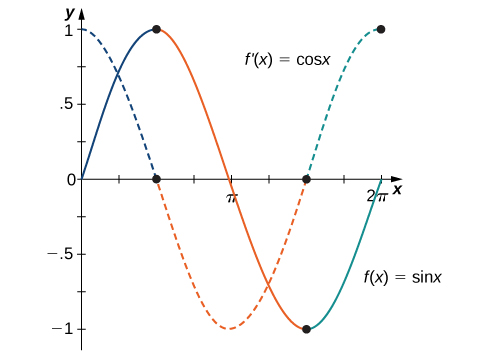
Encuentra la derivada de\(f(x)=5x^3\sin x\).
Solución
Usando la regla del producto, tenemos
\[ \begin{align*} f'(x) &=\dfrac{d}{dx}(5x^3)⋅\sin x+\dfrac{d}{dx}(\sin x)⋅5x^3 \\[4pt] &=15x^2⋅\sin x+\cos x⋅5x^3. \end{align*}\]
Después de simplificar, obtenemos
\[f′(x)=15x^2\sin x+5x^3\cos x. \nonumber \]
Encuentra la derivada de\(f(x)=\sin x\cos x.\)
- Pista
-
No olvides usar la regla del producto.
- Contestar
-
\[f′(x)=\cos^2x−\sin^2x \nonumber \]
Encuentra la derivada de\(g(x)=\dfrac{\cos x}{4x^2}\).
Solución
Al aplicar la regla del cociente, tenemos
\[g′(x)=\dfrac{(−\sin x)4x^2−8x(\cos x)}{(4x^2)^2}. \nonumber \]
Simplificando, obtenemos
\[g′(x)=\dfrac{−4x^2\sin x−8x\cos x}{16x^4}=\dfrac{−x\sin x−2\cos x}{4x^3}. \nonumber \]
Encuentra la derivada de\(f(x)=\dfrac{x}{\cos x}\).
- Pista
-
Usa la regla del cociente.
- Contestar
-
\(f'(x) = \dfrac{\cos x+x\sin x}{\cos^2x}\)
Una partícula se mueve a lo largo de un eje de coordenadas de tal manera que su posición en el tiempo\(t\) viene dada por\(s(t)=2\sin t−t\) for ¿\(0≤t≤2π.\)En qué momentos está la partícula en reposo?
Solución
Para determinar cuándo la partícula está en reposo, establecer\(s′(t)=v(t)=0.\) Empezar por encontrar\(s′(t).\) Obtenemos
\[s′(t)=2 \cos t−1, \nonumber \]
por lo que debemos resolver
\[2 \cos t−1=0\text{ for }0≤t≤2π. \nonumber \]
Las soluciones a esta ecuación son\(t=\dfrac{π}{3}\) y\(t=\dfrac{5π}{3}\). Así la partícula está en reposo a veces\(t=\dfrac{π}{3}\) y\(t=\dfrac{5π}{3}\).
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el momento\(t\) está dada por\(s(t)=\sqrt{3}t+2\cos t\) para ¿\(0≤t≤2π.\)En qué momentos está la partícula en reposo?
- Pista
-
Usa el ejemplo anterior como guía.
- Contestar
-
\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)
Derivadas de Otras Funciones Trigonométricas
Dado que las cuatro funciones trigonométricas restantes pueden expresarse como cocientes que involucran seno, coseno o ambos, podemos usar la regla del cociente para encontrar fórmulas para sus derivadas.
Encuentra la derivada de\(f(x)=\tan x.\)
Solución
Comience expresando\(\tan x \) como el cociente de\(\sin x\) y\(\cos x\):
\(f(x)=\tan x =\dfrac{\sin x}{\cos x}\).
Ahora aplica la regla del cociente para obtener
\(f′(x)=\dfrac{\cos x\cos x−(−\sin x)\sin x}{(\cos x)^2}\).
Simplificando, obtenemos
\[f′(x)=\dfrac{\cos^2x+\sin^2 x}{\cos^2x}. \nonumber \]
Reconociendo que\(\cos^2x+\sin^2x=1,\) por el teorema de Pitágoras, ahora tenemos
\[f′(x)=\dfrac{1}{\cos^2x} \nonumber \]
Por último, utilizar la identidad\(\sec x=\dfrac{1}{\cos x}\) para obtener
\(f′(x)=\text{sec}^2 x\).
Encuentra la derivada de\(f(x)=\cot x .\)
- Pista
-
Reescribe\(\cot x \) como\(\dfrac{\cos x}{\sin x}\) y usa la regla del cociente.
- Contestar
-
\(f′(x)=−\csc^2 x\)
Las derivadas de las funciones trigonométricas restantes se pueden obtener utilizando técnicas similares. Proporcionamos estas fórmulas en el siguiente teorema.
Las derivadas de las funciones trigonométricas restantes son las siguientes:
\ [\ begin {align}\ dfrac {d} {dx} (\ tan x) &=\ seg^2x\\ [4pt]\ dfrac {d} {dx} (
\ cot x) &=−\ csc^2x\\ [4pt]\ dfrac {d} {dx} (\ sec x) &=
\ seg x bronceado\ x\\ [4pt] dfrac {d} {dx} (\ sec x) &=\ seg x bronceado\ x
\ [4pt] dfrac {d} frac {d} {dx} (\ csc x) &=−\ csc x\ cot x.\ end {align}\ nonumber\]
Encuentra la ecuación de una línea tangente a la gráfica de\(f(x)=\cot x \) at\(x=\frac{π}{4}\).
Solución
Para encontrar la ecuación de la línea tangente, necesitamos un punto y una pendiente en ese punto. Para encontrar el punto, cómpule
\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\).
Así la línea tangente pasa por el punto\(\left(\frac{π}{4},1\right)\). A continuación, encuentra la pendiente encontrando la derivada\(f(x)=\cot x \) y evaluándola en\(\frac{π}{4}\):
\(f′(x)=−\csc^2 x\)y\(f′\left(\frac{π}{4}\right)=−\csc^2\left(\frac{π}{4}\right)=−2\).
Usando la ecuación de punto-pendiente de la línea, obtenemos
\(y−1=−2\left(x−\frac{π}{4}\right)\)
o equivalentemente,
\(y=−2x+1+\frac{π}{2}\).
Encuentra la derivada de\(f(x)=\csc x+x\tan x .\)
Solución
Para encontrar esta derivada, debemos usar tanto la regla de suma como la regla de producto. Usando la regla de suma, encontramos
\(f′(x)=\dfrac{d}{dx}(\csc x)+\dfrac{d}{dx}(x\tan x )\).
En el primer término,\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x ,\) y aplicando la regla del producto al segundo término obtenemos
\(\dfrac{d}{dx}(x\tan x )=(1)(\tan x )+(\sec^2 x)(x)\).
Por lo tanto, tenemos
\(f′(x)=−\csc x\cot x +\tan x +x\sec^2 x\).
Encuentra la derivada de\(f(x)=2\tan x −3\cot x .\)
- Pista
-
Utilice la regla para diferenciar un múltiplo constante y la regla para diferenciar una diferencia de dos funciones.
- Contestar
-
\(f′(x)=2\sec^2 x+3\csc^2 x\)
Encuentra la pendiente de la línea tangente a la gráfica de\(f(x)=\tan x \) at\(x=\dfrac{π}{6}\).
- Pista
-
Evaluar la derivada en\(x=\dfrac{π}{6}\).
- Contestar
-
\(\dfrac{4}{3}\)
Derivados de orden superior
Las derivadas de orden superior de\(\sin x\) y\(\cos x\) siguen un patrón de repetición. Siguiendo el patrón, podemos encontrar cualquier derivado de orden superior de\(\sin x\) y\(\cos x.\)
Encuentra las primeras cuatro derivadas de\(y=\sin x.\)
Solución
Cada paso en la cadena es sencillo:
\ [\ begin {align*} y&=\ sin x\\ [4pt]
\ dfrac {dy} {dx} &=\ cos x\\ [4pt]
\ dfrac {d^2y} {dx^2} &=−\ sin x\ [4pt]
\ dfrac {d^3y} {dx^3} &=−\ cos x\ [4pt]
\ dfrac {d^4y} {dx^4} &=\ sin x\ final {alinear*}\]
Análisis
Una vez que reconocemos el patrón de derivados, podemos encontrar cualquier derivada de orden superior determinando el paso en el patrón al que corresponde. Por ejemplo, cada cuarta derivada de\(\sin x\) iguales\(\sin x\), entonces
\[\dfrac{d^4}{dx^4}(\sin x)=\dfrac{d^8}{dx^8}(\sin x)=\dfrac{d^{12}}{dx^{12}}(\sin x)=…=\dfrac{d^{4n}}{dx^{4n}}(\sin x)=\sin x \nonumber \]
\[\dfrac{d^5}{dx^5}(\sin x)=\dfrac{d^9}{dx^9}(\sin x)=\dfrac{d^{13}}{dx^{13}}(\sin x)=…=\dfrac{d^{4n+1}}{dx^{4n+1}}(\sin x)=\cos x. \nonumber \]
Para\(y=\cos x\), encontrar\(\dfrac{d^4y}{dx^4}\).
- Pista
-
Ver el ejemplo anterior.
- Contestar
-
\(\cos x\)
Encuentra\(\dfrac{d^{74}}{dx^{74}}(\sin x)\).
Solución
Podemos ver de inmediato que para el derivado 74 de\(\sin x\),\(74=4(18)+2\), entonces
\[\dfrac{d^{74}}{dx^{74}}(\sin x)=\dfrac{d^{72+2}}{dx^{72+2}}(\sin x)=\dfrac{d^2}{dx^2}(\sin x)=−\sin x. \nonumber \]
Para\(y=\sin x\), encontrar\(\dfrac{d^{59}}{dx^{59}}(\sin x).\)
- Pista
-
\(\dfrac{d^{59}}{dx^{59}}(\sin x)=\dfrac{d^{4⋅14+3}}{dx^{4⋅14+3}}(\sin x)\)
- Contestar
-
\(−\cos x\)
Una partícula se mueve a lo largo de un eje de coordenadas de tal manera que su posición en el tiempo\(t\) viene dada por\(s(t)=2−\sin t\). Encontrar\(v(π/4)\) y\(a(π/4)\). Compara estos valores y decide si la partícula se está acelerando o desacelerando.
Solución
Primer hallazgo\(v(t)=s′(t)\)
\[v(t)=s′(t)=−\cos t . \nonumber \]
Por lo tanto,
\(v\left(\frac{π}{4}\right)=−\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).
A continuación, encuentra\(a(t)=v′(t)\). Así,\(a(t)=v′(t)=\sin t\) y tenemos
\(a\left(\frac{π}{4}\right)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\).
Desde\(v\left(\frac{π}{4}\right)=−\dfrac{\sqrt{2}}{2}<0\) y\(a\left(\frac{π}{4}\right)=\dfrac{\sqrt{2}}{2}>0\), vemos que la velocidad y la aceleración están actuando en direcciones opuestas; es decir, el objeto se está acelerando en la dirección opuesta a la dirección en la que está viajando. En consecuencia, la partícula se está desacelerando.
Un bloque unido a un resorte se mueve verticalmente. Su posición en el tiempo t viene dada por\(s(t)=2\sin t\). Encontrar\(v\left(\frac{5π}{6}\right)\) y\(a\left(\frac{5π}{6}\right)\). Compara estos valores y decide si el bloqueo se está acelerando o desacelerando.
- Pista
-
Use el Ejemplo\(\PageIndex{9}\) como guía.
- Contestar
-
\(v\left(\frac{5π}{6}\right)=−\sqrt{3}<0\)y\(a\left(\frac{5π}{6}\right)=−1<0\). El bloque se está acelerando.
Conceptos clave
- Podemos encontrar las derivadas de\(\sin x\) y\(\cos x\) usando la definición de derivada y las fórmulas límite encontradas anteriormente. Los resultados son
\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big)=−\sin x\).
- Con estas dos fórmulas, podemos determinar las derivadas de las seis funciones trigonométricas básicas.
Ecuaciones Clave
- Derivada de función sinusoidal
\(\dfrac{d}{dx}(\sin x)=\cos x\)
- Derivada de la función coseno
\(\dfrac{d}{dx}(\cos x)=−\sin x\)
- Derivada de la función tangente
\(\dfrac{d}{dx}(\tan x )=\sec^2x\)
- Derivada de la función cotangente
\(\dfrac{d}{dx}(\cot x )=−\csc^2x\)
- Derivada de la función secante
\(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)
- Derivada de la función cosecante
\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x \)