3.4: Derivados como tasas de cambio

Última actualización
Guardar como PDF

Page ID: 116648

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Determinar un nuevo valor de una cantidad a partir del valor anterior y la cantidad de cambio.
Calcular la tasa promedio de cambio y explicar en qué se diferencia de la tasa instantánea de cambio.
Aplicar tasas de cambio al desplazamiento, velocidad y aceleración de un objeto que se mueve a lo largo de una línea recta.
Predecir la población futura a partir del valor presente y la tasa de crecimiento poblacional.
Utilizar derivados para calcular el costo marginal y los ingresos en una situación de negocio.

En esta sección observamos algunas aplicaciones de la derivada centrándonos en la interpretación de la derivada como la tasa de cambio de una función. Estas aplicaciones incluyen aceleración y velocidad en física, tasas de crecimiento poblacional en biología y funciones marginales en economía.

Cantidad de fórmula de cambio

Una aplicación para derivados es estimar un valor desconocido de una función en un punto usando un valor conocido de una función en algún punto dado junto con su tasa de cambio en el punto dado. Si$f(x)$ es una función definida en un intervalo$[a,a+h]$, entonces la cantidad de cambio de$f(x)$ sobre el intervalo es el cambio en los$y$ valores de la función sobre ese intervalo y viene dada por

\[f(a+h)−f(a). \nonumber \]

La tasa promedio de cambio de la función$f$ en ese mismo intervalo es la relación entre la cantidad de cambio en ese intervalo y el cambio correspondiente en los$x$ valores. Está dado por

\[\frac{f(a+h)−f(a)}{h}. \nonumber \]

Como ya sabemos, la tasa instantánea de cambio de$f(x)$ at$a$ es su derivada

\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \nonumber \]

Para valores lo suficientemente pequeños de$h$,$f′(a)≈\frac{f(a+h)−f(a)}{h}$. Luego podemos resolver para$f(a+h)$ obtener la cantidad de fórmula de cambio:

\[f(a+h)≈f(a)+f′(a)h. \label{linapprox} \]

Podemos usar esta fórmula si solo conocemos$f(a)$$f′(a)$ y deseamos estimar el valor de$f(a+h)$. Por ejemplo, podemos utilizar la población actual de una ciudad y la tasa a la que está creciendo para estimar su población en un futuro próximo. Como podemos ver en la Figura$\PageIndex{1}$, estamos aproximando$f(a+h)$ por la$y$ coordenada a a+h en la línea tangente a$f(x)$ at$x=a$. Observe que la precisión de esta estimación depende del valor de así$h$ como del valor de$f′(a)$.

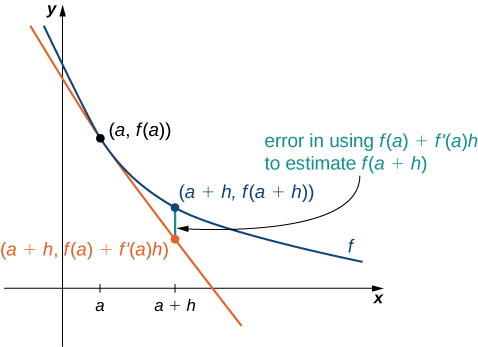
En el plano de coordenadas cartesianas con a y a + h marcadas en el eje x, se grafica la función f. Pasa por (a, f (a)) y (a + h, f (a + h)). Se dibuja una línea recta a través de (a, f (a)) siendo su pendiente la derivada en ese punto. Esta línea recta pasa por (a + h, f (a) + f' (a) h). Hay un segmento de línea que conecta (a + h, f (a + h)) y (a + h, f (a) + f' (a) h), y se marca que este es el error al usar f (a) + f' (a) h para estimar f (a + h). — Figura$\PageIndex{1}$: El nuevo valor de una cantidad cambiada es igual al valor original más la tasa de cambio multiplicada por el intervalo de cambio:$f(a+h)≈f(a)+f′(a)h.$

Ejemplo$\PageIndex{1}$: Estimating the Value of a Function

Si$f(3)=2$ y$f′(3)=5$, estimar$f(3.2)$.

Solución

Comience por encontrar$h$. Tenemos$h=3.2−3=0.2.$ Así,

$f(3.2)=f(3+0.2)≈f(3)+(0.2)f′(3)=2+0.2(5)=3.$

Ejercicio$\PageIndex{1}$

Dado$f(10)=−5$ y$f′(10)=6$, estimación$f(10.1)$.

Pista: Utilice el mismo proceso que en el ejemplo anterior.

Contestar: $−4.4$

Movimiento a lo largo de una línea

Otro uso para la derivada es analizar el movimiento a lo largo de una línea. Hemos descrito la velocidad como la velocidad de cambio de posición. Si tomamos la derivada de la velocidad, podemos encontrar la aceleración, o la tasa de cambio de velocidad. También es importante introducir la idea de velocidad, que es la magnitud de la velocidad. Así, podemos exponer las siguientes definiciones matemáticas.

Definición

Dejar$s(t)$ ser una función dando la posición de un objeto en el tiempo t.

La velocidad del objeto en el momento$t$ viene dada por$v(t)=s′(t)$.
La velocidad del objeto en el momento$t$ viene dada por$|v(t)|$.
La aceleración del objeto en$t$ viene dada por$a(t)=v′(t)=s''(t)$.

Ejemplo$\PageIndex{2}$: Comparing Instantaneous Velocity and Average Velocity

Se deja caer una pelota desde una altura de 64 pies. Su altura sobre el suelo (en pies)$t$ segundos después viene dada por$s(t)=−16t^2+64$.

$En el plano de coordenadas cartesianas, se grafica la función s (t) = −16t2 + 64. Esta función comienza en (0, 64) y disminuye a (0, 2).$

¿Cuál es la velocidad instantánea de la pelota cuando golpea el suelo?
¿Cuál es la velocidad promedio durante su caída?

Solución

Lo primero que hay que hacer es determinar cuánto tiempo tarda la pelota en llegar al suelo. Para ello, establezca$s(t)=0$. Resolviendo$−16t^2+64=0$, obtenemos$t=2$, por lo que tarda 2 segundos para que la pelota llegue al suelo.

La velocidad instantánea de la pelota a medida que golpea el suelo es$v(2)$. Ya que$v(t)=s′(t)=−32t$, obtenemos$v(t)=−64$ pies/s.
La velocidad promedio de la pelota durante su caída es

$v_{ave}=\frac{s(2)−s(0)}{2−0}=\frac{0−64}{2}=−32$pies/s.

Ejemplo$\PageIndex{3}$: Interpreting the Relationship between $v(t)$ and $a(t)$

Una partícula se mueve a lo largo de un eje de coordenadas en la dirección positiva hacia la derecha. Su posición en el momento$t$ viene dada por$s(t)=t^3−4t+2$. Encuentra$v(1)$$a(1)$ y usa estos valores para responder a las siguientes preguntas.

¿La partícula se mueve de izquierda a derecha o de derecha a izquierda en el momento$t=1$?
¿La partícula se está acelerando o desacelerando en el momento$t=1$?

Solución

Comience por encontrar$v(t)$ y$a(t)$.

$v(t) = s'(t) = 3t^2 - 4$y$a(t)=v′(t)=s''(t)=6t$.

Evaluando estas funciones en$t=1$, obtenemos$v(1)=−1$ y$a(1)=6$.

Porque$v(1)<0$, la partícula se mueve de derecha a izquierda.
Porque$v(1)<0$ y$a(1)>0$, la velocidad y la aceleración están actuando en direcciones opuestas. Es decir, la partícula se está acelerando en la dirección opuesta a la dirección en la que se desplaza, provocando$|v(t)|$ que disminuya. La partícula se está desacelerando.

Ejemplo$\PageIndex{4}$: Position and Velocity

La posición de una partícula que se mueve a lo largo de un eje de coordenadas viene dada por$s(t)=t^3−9t^2+24t+4,\; t≥0.$

Encuentra$v(t)$.
¿A qué hora (s) está la partícula en reposo?
¿En qué intervalos de tiempo se mueve la partícula de izquierda a derecha? ¿De derecha a izquierda?
Utilice la información obtenida para bosquejar la trayectoria de la partícula a lo largo de un eje de coordenadas.

Solución

a. La velocidad es la derivada de la función de posición:

$v(t)=s′(t)=3t^2−18t+24.$

b. La partícula está en reposo cuando$v(t)=0$, así se establece$3t^2−18t+24=0$. Factorizar el lado izquierdo de la ecuación produce$3(t−2)(t−4)=0$. Resolviendo, encontramos que la partícula está en reposo en$t=2$ y$t=4$.

c. La partícula se mueve de izquierda a derecha cuando$v(t)>0$ y de derecha a izquierda cuando$v(t)<0$. La figura$\PageIndex{2}$ da el análisis del signo de$v(t)$ for$t≥0$, pero no representa el eje a lo largo del cual se mueve la partícula.

Una línea numéricamarcada con 0, 2 y 4. Entre 0 y 2, hay un signo más. Por encima de 2, hay un 0. Entre 2 y 4 hay un signo negativo. Por encima de 4 hay un 0. Después de 4 hay un signo más y v (t). — Figura:El$\PageIndex{2}$ signo de determina$v(t)$ la dirección de la partícula.

Desde$3t^2−18t+24>0$ el momento$[0,2)∪(4,+∞)$, la partícula se mueve de izquierda a derecha en estos intervalos.
Desde$3t^2−18t+24<0$ el momento$(2,4)$, la partícula se mueve de derecha a izquierda en este intervalo.

d. Antes de poder esbozar la gráfica de la partícula, necesitamos conocer su posición en el momento en que comienza a moverse$(t=0)$ y en los momentos en que cambia de dirección$(t=2,4)$. Tenemos$s(0)=4$,$s(2)=24$, y$s(4)=20$. Esto significa que la partícula comienza en el eje de coordenadas$4$ y cambia de dirección en$24$ y$20$ sobre el eje de coordenadas. La trayectoria de la partícula se muestra en un eje de coordenadas en la Figura$\PageIndex{3}$.

Se da una línea numérica y por encima de ella una línea serpientes, comenzando en t = 0 por encima de 4 en la recta numérica. Entonces la línea en t = 2 está por encima de 24 en la recta numéricos. Entonces la línea disminuye en t = 4 para estar por encima de 20 en la recta numérica, punto en el que la línea invierte de nuevo dirección y aumenta indefinidamente. — Figura$\PageIndex{3}$: La trayectoria de la partícula se puede determinar analizando$v(t)$.

Ejercicio$\PageIndex{2}$

Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el momento$t$ viene dada por$s(t)=t^2−5t+1$. ¿La partícula se mueve de derecha a izquierda o de izquierda a derecha en el momento$t=3$?

Pista: Encuentra$v(3)$ y mira el letrero.

Contestar: de izquierda a derecha

Cambio poblacional

Además de analizar velocidad, velocidad, aceleración y posición, podemos usar derivados para analizar diversos tipos de poblaciones, incluyendo aquellas tan diversas como colonias de bacterias y ciudades. Podemos utilizar una población actual, junto con una tasa de crecimiento, para estimar el tamaño de una población en el futuro. La tasa de crecimiento poblacional es la tasa de cambio de una población y en consecuencia puede ser representada por la derivada del tamaño de la población.

Definición

Si$P(t)$ es el número de entidades presentes en una población, entonces la tasa de crecimiento poblacional de$P(t)$ se define como$P′(t)$.

Ejemplo$\PageIndex{5}$: Estimating a Population

La población de una ciudad se triplica cada 5 años. Si su población actual es de 10 mil, ¿cuál será su población aproximada dentro de 2 años?

Solución

$P(t)$Sea la población (en miles)$t$ años a partir de ahora. Así, lo sabemos$P(0)=10$ y con base en la información, nos anticipamos$P(5)=30$. Ahora estime$P′(0)$, la tasa de crecimiento actual, utilizando

$P′(0)≈\frac{P(5)−P(0)}{5−0}=\frac{30−10}{5}=4$.

Aplicando la Ecuación\ ref {linapprox} a$P(t)$, podemos estimar la población dentro de 2 años escribiendo

$P(2)≈P(0)+(2)P′(0)≈10+2(4)=18$;

así, en 2 años la población será de 18 mil.

Ejercicio$\PageIndex{3}$

Se sabe que la población actual de una colonia de mosquitos es de 3 mil; es decir,$P(0)=3,000$. Si$P′(0)=100$, estimar el tamaño de la población en 3 días, donde$t$ se mide en días.

Pista: Uso$P(3)≈P(0)+3P′(0)$

Contestar: 3,300

Cambios en Costo e Ingresos

Además de analizar el movimiento a lo largo de una línea y el crecimiento de la población, los derivados son útiles para analizar los cambios en costos, ingresos y ganancias. El concepto de función marginal es común en los campos de los negocios y la economía e implica el uso de derivados. El costo marginal es el derivado de la función de costo. El ingreso marginal es el derivado de la función de ingresos. El beneficio marginal es el derivado de la función de ganancia, que se basa en la función de costo y la función de ingresos.

Definición

Si$C(x)$ es el costo de producir$x$ artículos, entonces el costo marginal$MC(x)$ es$MC(x)=C′(x)$.
Si$R(x)$ es el ingreso obtenido de la venta de$x$ artículos, entonces el ingreso marginal$MR(x)$ es$MR(x)=R′(x)$.
Si$P(x)=R(x)−C(x)$ es el beneficio obtenido de la venta de$x$ artículos, entonces el beneficio marginal$MP(x)$ se define como$MP(x)=P′(x)=MR(x)−MC(x)=R′(x)−C′(x)$.

Podemos aproximarnos aproximadamente

\[MC(x)=C′(x)=\lim_{h→0}\frac{C(x+h)−C(x)}{h} \nonumber \]

eligiendo un valor apropiado para$h$. Dado que$x$ representa objetos, un valor razonable y pequeño para$h$ es 1. Así, al sustituir$h=1$, obtenemos la aproximación$MC(x)=C′(x)≈C(x+1)−C(x)$. En consecuencia,$C′(x)$ para un valor dado de$x$ puede pensarse como el cambio en el costo asociado con la producción de un artículo adicional. De manera similar,$MR(x)=R′(x)$ se aproxima a los ingresos obtenidos por la venta de un artículo adicional, y$MP(x)=P′(x)$ se aproxima a la ganancia obtenida al producir y vender un artículo adicional.

Ejemplo$\PageIndex{6}$: Applying Marginal Revenue

Supongamos que el número de cenas de barbacoa que se pueden vender,$x$, puede relacionarse con el precio cobrado,$p$, por la ecuación$p(x)=9−0.03x,0≤x≤300$.

En este caso, los ingresos en dólares obtenidos por la venta de cenas de$x$ barbacoa son dados por

$R(x)=xp(x)=x(9−0.03x)=−0.03x^2+9x\;\text{ for }0≤x≤300$.

Utilice la función de ingresos marginales para estimar los ingresos obtenidos de la venta de la cena de$101^{\text{st}}$ barbacoa. Compare esto con los ingresos reales obtenidos por la venta de esta cena.

Solución

Primero, encuentra la función de ingresos marginales:$MR(x)=R′(x)=−0.06x+9.$

A continuación, utilice$R′(100)$ para aproximar$R(101)−R(100)$, los ingresos obtenidos de la venta de la$101^{\text{st}}$ cena. Ya que$R′(100)=3$, los ingresos obtenidos por la venta de la$101^{\text{st}}$ cena son de aproximadamente $3.

Los ingresos reales obtenidos de la venta de la$101^{\text{st}}$ cena son

$R(101)−R(100)=602.97−600=2.97,$o$$2.97.$

El ingreso marginal es una estimación bastante buena en este caso y tiene la ventaja de ser fácil de calcular.

Ejercicio$\PageIndex{4}$

Supongamos que la ganancia obtenida de la venta de cenas$x$ de pescado frita viene dada por$P(x)=−0.03x^2+8x−50$. Utilizar la función de beneficio marginal para estimar el beneficio de la venta de la cena$101^{\text{st}}$ de pescado frita.

Pista: Úselo$P′(100)$ para aproximar$P(101)−P(100)$.

Contestar: $2

Conceptos clave

Utilizando$f(a+h)≈f(a)+f′(a)h$, es posible estimar$f(a+h)$ dado$f′(a)$ y$f(a)$.
La tasa de cambio de posición es la velocidad, y la tasa de cambio de velocidad es la aceleración. La velocidad es el valor absoluto, o magnitud, de la velocidad.
La tasa de crecimiento poblacional y la población actual pueden utilizarse para predecir el tamaño de una población futura.
Las funciones de costo marginal, ingresos marginales y ganancias marginales se pueden utilizar para predecir, respectivamente, el costo de producir un artículo más, los ingresos obtenidos al vender un artículo más y el beneficio obtenido al producir y vender un artículo más.

Glosario

aceleración: es la tasa de cambio de la velocidad, es decir, la derivada de la velocidad

cantidad de cambio: la cantidad de una función a$f(x)$ lo largo de un intervalo$[x,x+h] is f(x+h)−f(x)$

tasa promedio de cambio: es una función a$f(x)$ lo largo de un intervalo$[x,x+h]$ es$\frac{f(x+h)−f(a)}{b−a}$

costo marginal: es el derivado de la función de costo, o el costo aproximado de producir un artículo más

ingresos marginales: es el derivado de la función de ingresos, o los ingresos aproximados obtenidos por la venta de un artículo más

beneficio marginal: es la derivada de la función de ganancia, o la ganancia aproximada obtenida al producir y vender un artículo más

tasa de crecimiento poblacional: es el derivado de la población con respecto al tiempo

velocidad: es el valor absoluto de la velocidad, es decir,$|v(t)|$ es la velocidad de un objeto en el momento$t$ cuya velocidad viene dada por$v(t)$

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{1}\): Estimating the Value of a Function

Ejercicio\(\PageIndex{1}\)

Definición

Ejemplo\(\PageIndex{2}\): Comparing Instantaneous Velocity and Average Velocity

Ejemplo\(\PageIndex{3}\): Interpreting the Relationship between \(v(t)\) and \(a(t)\)

Ejemplo\(\PageIndex{4}\): Position and Velocity

Ejercicio\(\PageIndex{2}\)

Definición

Ejemplo\(\PageIndex{5}\): Estimating a Population

Ejercicio\(\PageIndex{3}\)

Definición

Ejemplo\(\PageIndex{6}\): Applying Marginal Revenue

Ejercicio\(\PageIndex{4}\)