4.3E: Ejercicios para la Sección 4.3

Última actualización
Guardar como PDF

Page ID: 116417

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) En el precálculo, aprendiste una fórmula para la posición del máximo o mínimo de una ecuación cuadrática$y=ax^2+bx+c$, que era$m=−\frac{b}{2a}$. Demuestra esta fórmula usando cálculo.

2) Si estás encontrando un mínimo absoluto a lo largo de un intervalo ¿$[a,b],$por qué necesitas verificar los puntos finales? Dibuja una gráfica que apoye tu hipótesis.

Responder: En un intervalo cerrado, los puntos finales a menudo se encuentran por encima o por debajo de cualquier extremo local (relativo). Las respuestas pueden variar para la gráfica.

3) Si estás examinando una función a lo largo de un intervalo$(a,b),$ para$a$ y$b$ finito, ¿es posible no tener un máximo absoluto o un mínimo absoluto?

4) Cuando estés comprobando puntos críticos para localizar los extremos de una función$f$, explica por qué también necesitas determinar puntos donde$f'(x)$ está indefinido. Dibuja una gráfica para apoyar tu explicación.

Responder: Los puntos en la gráfica de$f$ donde hay una esquina, una cúspide, o una discontinuidad de salto o discontinuidad removible pueden ser fácilmente extremos absolutos (o locales) de la función. Las respuestas pueden variar para la gráfica.

5) ¿Se puede tener un máximo absoluto finito por$y=ax^2+bx+c$ más$(−∞,∞)$? Explique por qué o por qué no usando argumentos gráficos.

6) ¿Se puede tener un máximo absoluto finito para$y=ax^3+bx^2+cx+d$$(−∞,∞)$ sobreasumir que$a$ es distinto de cero? Explique por qué o por qué no usando argumentos gráficos.

Responder: No; las respuestas variarán

7) Dejar$m$ ser el número de mínimos locales y$M$ ser el número de máximos locales. ¿Se puede crear una función donde$M>m+2$? Dibuja una gráfica para apoyar tu explicación.

8) ¿Es posible tener más de un máximo absoluto? Usa un argumento gráfico para probar tu hipótesis.

Responder: Dado que el máximo absoluto es el valor de la función (salida) en lugar del valor x, la respuesta es no; las respuestas variarán

9) ¿Es posible no tener mínimo o máximo absoluto para una función? Si es así, construya tal función. Si no, explique por qué esto no es posible.

10) [T] Grafica la función ¿$y=e^{ax}.$Para qué valores de$a$, en cualquier dominio infinito, tendrás un mínimo absoluto y un máximo absoluto?

Responder: Cuando$a=0$

En los ejercicios 11 - 14, determinar dónde ocurren los máximos y mínimos locales y absolutos en la gráfica dada. Supongamos que los dominios son intervalos cerrados a menos que se especifique

11)

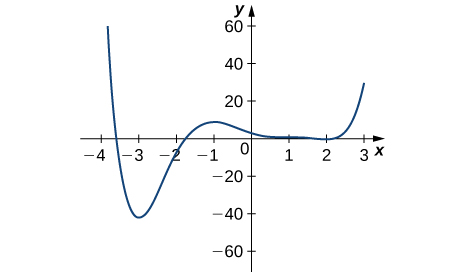
$La función graficada comienza en (−4, 60), disminuye rápidamente a (−3, −40), aumenta a (−1, 10) antes de disminuir lentamente a (2, 0), momento en el que aumenta rápidamente a (3, 30).$

12)

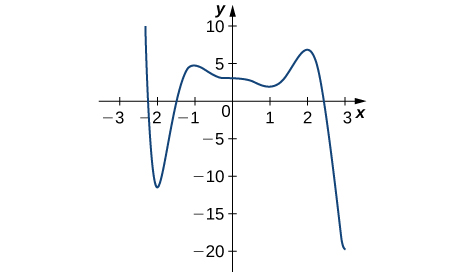
$La función graficada comienza en (−2.2, 10), disminuye rápidamente a (−2, −11), aumenta a (−1, 5) antes de disminuir lentamente a (1, 3), momento en el que aumenta a (2, 7), y luego disminuye a (3, −20).$

Responder: Mínimo absoluto a 3; Máximo absoluto en −2.2; mínimos locales en −2, 1; máximos locales en −1, 2

13)

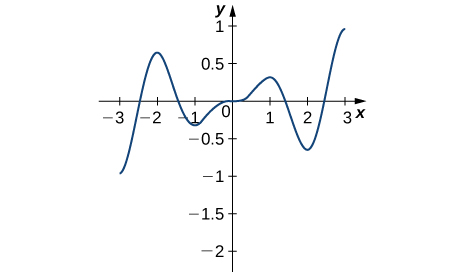
$La función graficada comienza en (−3, −1), aumenta rápidamente a (−2, 0.7), disminuye a (−1, −0.25) antes de disminuir lentamente a (1, 0.25), momento en el que disminuye a (2, 0.7), y luego aumenta a (3, 1).$

14)

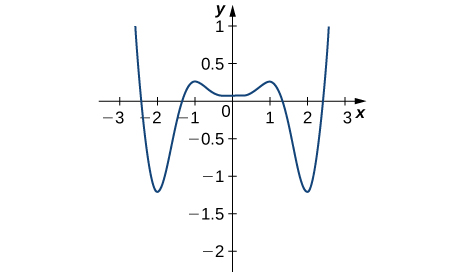
$La función graficada comienza en (−2.5, 1), disminuye rápidamente a (−2, −1.25), aumenta a (−1, 0.25) antes de disminuir lentamente a (0, 0.2), momento en el que aumenta lentamente a (1, 0.25), luego disminuye rápidamente a (2, −1.25), y finalmente aumenta a (2.5, 1).$

Responder: Mínimos absolutos a −2, 2; máximos absolutos a −2.5, 2.5; mínimo local a 0; máximos locales en −1, 1

Para los ejercicios 15 - 18, dibuje gráficas de$f(x)$, que es continuo, a lo largo del intervalo$[−4,4]$ con las siguientes propiedades:

15) Máximo absoluto en$x=2$ y mínimos absolutos en$x=±3$

16) Mínimo absoluto en$x=1$ y máximo absoluto en$x=2$

Responder: Las respuestas pueden variar.

17) Máximo absoluto al mínimo$x=4,$ absoluto en el máximo$x=−1,$ local en$x=−2,$ y un punto crítico que no es un máximo o mínimo en$x=2$

18) Máximo absoluto en$x=2$ y$x=−3$, mínimo local en$x=1$, y mínimo absoluto en$x=4$

Responder: Las respuestas pueden variar.

En los ejercicios 19 - 28, encuentra los puntos críticos en los dominios de las funciones dadas.

19)$y=4x^3−3x$

20)$y=4\sqrt{x}−x^2$

Responder: $x=1$

21)$y=\dfrac{1}{x−1}$

22)$y=\ln(x−2)$

Responder: Ninguno

23)$y=\tan(x)$

24)$y=\sqrt{4−x^2}$

Responder: $x=0$

25)$y=x^{3/2}−3x^{5/2}$

26)$y=\dfrac{x^2−1}{x^2+2x−3}$

Responder: Ninguno

27)$y=\sin^2(x)$

28)$y=x+\dfrac{1}{x}$

Responder: $x=−1$y$x = 1$

En los ejercicios 29 - 39, encuentra los máximos locales y/o absolutos para las funciones sobre el dominio especificado.

29)$f(x)=x^2+3$ sobre$[−1,4]$

30)$y=x^2+\dfrac{2}{x}$ sobre$[1,4]$

Responder: Máximo absoluto:$x=4, y=\frac{33}{2}$; mínimo absoluto:$x=1, y=3$

31)$y=(x−x^2)^2$ sobre$[−1,1]$

32)$y=\dfrac{1}{x−x^2}$ sobre$[0,1]$

Responder: Mínimo absoluto:$x=\frac{1}{2}, y=4$

33)$y=\sqrt{9−x}$ sobre$[1,9]$

34)$y=x+\sin(x)$ sobre$[0,2π]$

Responder: Máximo absoluto: mínimo$x=2π, y=2π;$ absoluto:$x=0, y=0$

35)$y=\dfrac{x}{1+x}$ sobre$[0,100]$

36)$y=|x+1|+|x−1|$ sobre$[−3,2]$

Responder: Máximo absoluto: mínimo$x=−3, y = 6;$ absoluto:$−1≤x≤1, y=2$

37)$y=\sqrt{x}−\sqrt{x^3}$ sobre$[0,4]$

38)$y=\sin x+\cos x$ sobre$[0,2π]$

Contestar: Máximo absoluto:$x=\frac{π}{4}, y=\sqrt{2}$; mínimo absoluto:$x=\frac{5π}{4}, y=−\sqrt{2}$

39)$y=4\sin θ−3\cos θ$ sobre$[0,2π]$

En los ejercicios 40 - 45, encuentra los mínimos y máximos locales y absolutos para las funciones sobre$(−∞,∞).$

40)$y=x^2+4x+5$

Contestar: Mínimo absoluto:$x=−2, y=1$

41)$y=x^3−12x$

42)$y=3x^4+8x^3−18x^2$

Contestar: Mínimo absoluto: máximo$x=−3, y=−135;$ local:$x=0, y=0$; mínimo local:$x=1, y=−7$

43)$y=x^3(1−x)^6$

44)$y=\dfrac{x^2+x+6}{x−1}$

Contestar: Máximo local:$x=1−2\sqrt{2}, y=3−4\sqrt{2}$; mínimo local:$x=1+2\sqrt{2}, y=3+4\sqrt{2}$

45)$y=\dfrac{x^2−1}{x−1}$

En los ejercicios 46 - 50, utilice una calculadora para graficar la función y estimar los máximos y mínimos absolutos y locales. Entonces, resolver por ellos de manera explícita.

46) [T]$y=3x\sqrt{1−x^2}$

Contestar: Máximo absoluto: mínimo$x=\frac{\sqrt{2}}{2}, y=\frac{3}{2};$ absoluto:$x=−\frac{\sqrt{2}}{2}, y=−\frac{3}{2}$

47) [T]$y=x+\sin(x)$

48) [T]$y=12x^5+45x^4+20x^3−90x^2−120x+3$

Contestar: Máximo local:$x=−2,y=59$; mínimo local:$x=1, y=−130$

49) [T]$y=\dfrac{x^3+6x^2−x−30}{x−2}$

50) [T]$y=\dfrac{\sqrt{4−x^2}}{\sqrt{4+x^2}}$

Contestar: Máximo absoluto: mínimo$x=0, y=1;$ absoluto:$x=−2,2, y=0$

51) Una empresa que produce teléfonos celulares tiene una función de costo de$C=x^2−1200x+36,400,$ donde$C$ se cuesta en dólares y$x$ es el número de celulares producidos (en miles). ¿Cuántas unidades de celular (en miles) minimiza esta función de costo?

52) Se lanza una pelota al aire y su posición viene dada por$h(t)=−4.9t^2+60t+5m.$ Encuentra la altura a la que la pelota deja de ascender. ¿Cuánto tiempo después de que se lanza sucede esto?

Contestar: $h=\frac{9245}{49}$m,$t=\frac{300}{49}$ s

Para los ejercicios 53-54, considere la producción de oro durante la fiebre del oro de California (1848—1888). La producción de oro puede ser modelada por$G(t)=\dfrac{(25t)}{(t^2+16)}$, donde$t$ está el número de años desde que comenzó la fiebre$(0≤t≤40)$ y$G$ es onzas de oro producidas (en millones). En la siguiente figura se muestra un resumen de los datos.

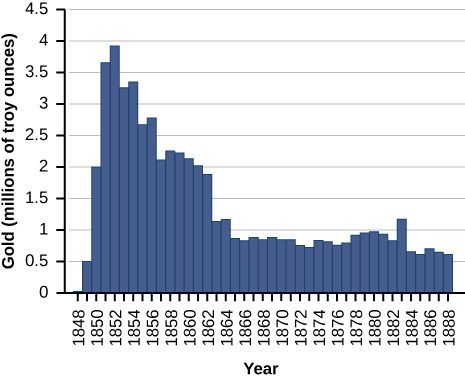
$El gráfico de barras muestra oro (en millones de onzas troy) por año, comenzando en 1848 y terminando en 1888. En 1848, la gráfica de barras muestra 0.05; en 1849, 0.5; en 1850, 2; en 1851, 3.6; en 1852, 3.9; en 1853, 3.3; en 1854, 3.4; en 1855, 2.6; en 1856, 2.75; en 1857, 2.1; en 1858, 2.2; en 1859, 2.15; en 1860, 2.1; en 1861, 2; en 1862, 1.8; en 1863, 1.1; en 1864, 1.15; en 1865, 0.9; en 1866, 0.85; en 1867, 0.9; en 1868, 0.85 ; en 1869, 0.9; en 1870, 0.85; en 1871, 0.85; en 1872, 0.75; en 1873, 0.7; en 1874, 0.8; en 1875, 0.75; en 1876, 0.7; en 1877, 0.73; en 1878, 0.9; en 1879, 0.95; en 1880, 1; en 1881, 0.95; en 1882, 0.85; en 1883, 1.1; en 1884, 0.6; en 1885, 0.55; en 1886, 0.65; en 1887, 0.6; y en 1888, 0.55.$

53) Encontrar cuándo ocurrió la producción máxima (local y global) de oro, y la cantidad de oro producida durante ese máximo.

54) Encontrar cuándo ocurrió la producción mínima (local y global) de oro. ¿Cuál fue la cantidad de oro producida durante este mínimo?

Contestar: El mínimo global fue en 1848, cuando no se produjo oro.

En los ejercicios 55 y 56, encuentra los puntos críticos, máximos y mínimos para las funciones por partes dadas.

55)$y= \begin{cases} x^2−4x, & \text{if }0≤x≤1\\x^2−4, & \text{if }1<x≤2 \end{cases}$

56)$y=\begin{cases}x^2+1, & \text{if }x≤1 \\ x^2−4x+5, & \text{if }x>1\end{cases}$

Contestar: Mínimos absolutos:$x=0, x=2, y=1$; máximo local en$x=1, y=2$

En los ejercicios 57 - 58, encuentra los puntos críticos de las siguientes funciones genéricas. ¿Son máximos, mínimos o ninguno? Expresar las condiciones necesarias.

57)$y=ax^2+bx+c,$ dado que$a>0$

58)$y=(x−1)^a$, dado que$a>1$

Contestar: Sin máximo/mínimos si$a$ es impar, mínimo en$x=1$ si$a$ es par

Colaboradores y Atribuciones

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added answers for exercises 2 and 4.