4.3: Maxima y Minima

Última actualización
Guardar como PDF

Page ID: 116401

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Objetivos de aprendizaje

Definir los extremos absolutos.
Definir los extremos locales.
Explicar cómo encontrar los puntos críticos de una función en un intervalo cerrado.
Describir cómo usar puntos críticos para ubicar los extremos absolutos en un intervalo cerrado.

Dada una función particular, a menudo nos interesa determinar los valores más grandes y más pequeños de la función. Esta información es importante en la creación de gráficas precisas. Encontrar los valores máximos y mínimos de una función también tiene importancia práctica, ya que podemos utilizar este método para resolver problemas de optimización, como maximizar el beneficio, minimizar la cantidad de material utilizado en la fabricación de una lata de aluminio, o encontrar la altura máxima que puede alcanzar un cohete. En esta sección, analizamos cómo usar derivados para encontrar los valores más grandes y más pequeños para una función.

Absoluta Extrema

Considera la función\(f(x)=x^2+1\) a lo largo del intervalo\((−∞,∞)\). Como\(x→±∞, f(x)→∞\). Por lo tanto, la función no tiene un valor mayor. No obstante, ya que\(x^2+1≥1\) para todos los números reales\(x\) y\(x^2+1=1\) cuándo\(x=0\), la función tiene un valor menor,\(1\), cuándo\(x=0\). Decimos que\(1\) es el mínimo absoluto de\(f(x)=x^2+1\) y se da en\(x=0\). Decimos que\(f(x)=x^2+1\) no tiene un máximo absoluto (Figura\(\PageIndex{1}\)).

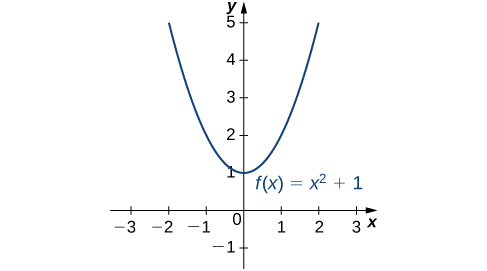
Se grafica la función f (x) = x^2 + 1, y su mínimo de 1 se ve en x = 0. — Figura\(\PageIndex{1}\): La función dada tiene un mínimo absoluto de\(1\) at\(x=0\). La función no tiene un máximo absoluto.

Definición: Absolute Extrema

Dejar\(f\) ser una función definida sobre un intervalo\(I\) y let\(c∈I\). Decimos que\(f\) tiene un máximo\(I\) absoluto encendido a\(f(c)≥f(x)\) por\(c\) si fuera por todos\(x∈I\). Decimos que\(f\) tiene un mínimo\(I\) absoluto en\(f(c)≤f(x)\) por\(c\) si es para todos\(x∈I\). Si\(f\) tiene un máximo absoluto on\(I\) at\(c\) o un mínimo absoluto on\(I\) at\(c\), decimos que\(f\) tiene un extremo absoluto on\(I\) at\(c\).

Antes de continuar, señalemos dos temas importantes respecto a esta definición. En primer lugar, el término absoluto aquí no se refiere al valor absoluto. Un extremo absoluto puede ser positivo, negativo o cero. Segundo, si una función\(f\) tiene un extremo absoluto sobre un intervalo\(I\) at\(c\), el extremo absoluto es\(f(c)\). El número real\(c\) es un punto en el dominio en el que se produce el extremo absoluto. Por ejemplo, considere la función\(f(x)=1/(x^2+1)\) sobre el intervalo\((−∞,∞)\). Desde

\[f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber \]

para todos los números reales\(x\), decimos que\(f\) tiene un máximo absoluto sobre\((−∞,∞)\) at\(x=0\). El máximo absoluto es\(f(0)=1\). Ocurre en\(x=0\), como se muestra en la Figura\(\PageIndex{2}\) (b).

Una función puede tener tanto un máximo absoluto como un mínimo absoluto, solo un extremo, o ninguno. La figura\(\PageIndex{2}\) muestra varias funciones y algunas de las diferentes posibilidades respecto a los extremos absolutos. Sin embargo, el siguiente teorema, denominado Teorema del Valor Extremo, garantiza que una función continua\(f\) sobre un intervalo cerrado y delimitado\([a,b]\) tiene tanto un máximo absoluto como un mínimo absoluto.

Esta figura tiene seis partes a, b, c, d, e y f. En la figura a, se muestra la línea f (x) = x^3, y se observa que no tiene mínimo absoluto ni máximo absoluto. En la figura b, se muestra la línea f (x) = 1/ (x^2 + 1), que está cerca de 0 en la mayor parte de su longitud y se eleva a un bache en (0, 1); no tiene mínimo absoluto, pero sí tiene un máximo absoluto de 1 en x = 0. En la figura c, se muestra la línea f (x) = cos x, que tiene mínimos absolutos de −1 a ±π, ±3π,... y máximos absolutos de 1 a 0, ±2π, ±4π,... En la figura d, se muestra la función por tramos f (x) = 2 — x^2 para 0 ≤ x < 2 y x — 3 para 2 ≤ x ≤ 4, con máximo absoluto de 2 a x = 0 y sin mínimo absoluto. En la figura e, la función f (x) = (x — 2) 2 se muestra en [1, 4], que tiene un máximo absoluto de 4 en x = 4 y un mínimo absoluto de 0 en x = 2. En la figura f, la función f (x) = x/ (2 − x) se muestra en [0, 2), con mínimo absoluto de 0 a x = 0 y sin máximo absoluto. — Figura\(\PageIndex{2}\): Las gráficas (a), (b) y (c) muestran varias posibilidades para extremos absolutos para funciones con un dominio de\((−∞,∞).\) Las gráficas (d), (e) y (f) muestran varias posibilidades para extremos absolutos para funciones con un dominio que es un intervalo acotado.

Teorema\(\PageIndex{1}\): Extreme Value Theorem

Si\(f\) es una función continua sobre el intervalo cerrado y delimitado\([a,b]\), entonces hay un punto en\([a,b]\) el que\(f\) tiene un máximo absoluto sobre\([a,b]\) y hay un punto en\([a,b]\) el que\(f\) tiene un mínimo absoluto sobre\([a,b]\).

La prueba del teorema del valor extremo está fuera del alcance de este texto. Por lo general, se prueba en un curso sobre análisis real. Hay un par de puntos clave a tener en cuenta sobre la afirmación de este teorema. Para que se aplique el teorema del valor extremo, la función debe ser continua a lo largo de un intervalo cerrado y delimitado. Si el intervalo\(I\) está abierto o la función tiene incluso un punto de discontinuidad, es posible que la función no tenga un máximo absoluto o un mínimo absoluto sobre\(I\). Por ejemplo, considere las funciones que se muestran en la Figura\(\PageIndex{2}\) (d), (e) y (f). Las tres funciones se definen a lo largo de intervalos delimitados. Sin embargo, la función en la gráfica (e) es la única que tiene tanto un máximo absoluto como un mínimo absoluto sobre su dominio. El teorema del valor extremo no se puede aplicar a las funciones de las gráficas (d) y (f) porque ninguna de estas funciones es continua a lo largo de un intervalo cerrado y delimitado. Aunque la función en la gráfica (d) se define sobre el intervalo cerrado\([0,4]\), la función es discontinua en\(x=2\). La función tiene un máximo absoluto sobre\([0,4]\) pero no tiene un mínimo absoluto. La función en la gráfica (f) es continua a lo largo del intervalo semiabierto\([0,2)\), pero no se define en\(x=2\), y por lo tanto no es continua en un intervalo cerrado y delimitado. La función tiene un mínimo absoluto sobre\([0,2)\), pero no tiene un máximo absoluto sobre\([0,2)\). Estos dos gráficos ilustran por qué una función a lo largo de un intervalo delimitado puede no tener un máximo absoluto y/o un mínimo absoluto.

Antes de ver cómo encontrar los extremos absolutos, examinemos el concepto relacionado de extrema local. Esta idea es útil para determinar dónde ocurren los extremos absolutos.

Puntos Extremos y Críticos Locales

Considera la función que\(f\) se muestra en la Figura\(\PageIndex{3}\). La gráfica se puede describir como dos montañas con un valle en el medio. El valor máximo absoluto de la función ocurre en el pico más alto, at\(x=2\). No obstante, también\(x=0\) es un punto de interés. Aunque no\(f(0)\) es el mayor valor de\(f\), el valor\(f(0)\) es mayor que\(f(x)\) para todos\(x\) cerca de 0. Decimos que\(f\) tiene un máximo local en\(x=0\). De igual manera, la función\(f\) no tiene un mínimo absoluto, pero sí tiene un mínimo local en\(x=1\) porque\(f(1)\) es menor que\(f(x)\) para\(x\) cerca de 1.

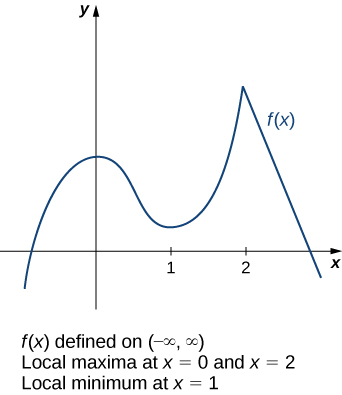
Se muestra la función f (x), que se curva hacia arriba desde el cuadrante III, se ralentiza en el cuadrante II, logra un máximo local en el eje y, disminuye para lograr un mínimo local en el cuadrante I en x = 1, aumenta a un máximo local en x = 2 que es mayor que el otro máximo local, y luego disminuye rápidamente a través de cuadrante IV. — Figura\(\PageIndex{3}\): Esta función\(f\) tiene dos máximos locales y un mínimo local. El máximo local at\(x=2\) es también el máximo absoluto.

Definición: Local Extrema

Una función\(f\) tiene un máximo local en\(c\) si existe un intervalo abierto\(I\) que contenga\(c\) tal que\(I\) esté contenido en el dominio de\(f\) y\(f(c)≥f(x)\) para todos\(x∈I\). Una función\(f\) tiene un mínimo local en\(c\) si existe un intervalo abierto\(I\) que contenga\(c\) tal que\(I\) esté contenido en el dominio de\(f\) y\(f(c)≤f(x)\) para todos\(x∈I\). Una función\(f\) tiene un extremo local en\(c\) si\(f\) tiene un máximo local en\(c\) o\(f\) tiene un mínimo local en\(c\).

Tenga en cuenta que si\(f\) tiene un extremo absoluto en\(c\) y\(f\) se define sobre un intervalo que contiene\(c\), entonces también\(f(c)\) se considera un extremo local. Si\(f\) se produce un extremo absoluto para una función en un punto final, no consideramos que sea un extremo local, sino que nos referimos a eso como extremo extremo de extremo.

Dada la gráfica de una función\(f\), a veces es fácil ver dónde ocurre un máximo local o mínimo local. Sin embargo, no siempre es fácil de ver, ya que las características interesantes en la gráfica de una función pueden no ser visibles porque ocurren a muy pequeña escala. Además, es posible que no tengamos una gráfica de la función. En estos casos, ¿cómo podemos usar una fórmula para una función para determinar dónde ocurren estos extremos?

Para responder a esta pregunta,\(\PageIndex{3}\) volvamos a ver Figura. Los extremos locales ocurren en\(x=0, x=1,\) y\(x=2.\) Observe que en\(x=0\) y\(x=1\), la derivada\(f'(x)=0\). At\(x=2\), la derivada\(f'(x)\) no existe, ya que la función\(f\) tiene una esquina ahí. De hecho, si\(f\) tiene un extremo local en un punto\(x=c\), la derivada\(f'(c)\) debe satisfacer una de las siguientes condiciones: cualquiera\(f'(c)=0\) o\(f'(c)\) es indefinida. Tal valor\(c\) se conoce como punto crítico y es importante para encontrar valores extremos para funciones.

Definición: Puntos críticos

Dejar\(c\) ser un punto interior en el dominio de\(f\). Decimos que\(c\) es un punto crítico de\(f\) si\(f'(c)=0\) o\(f'(c)\) es indefinido.

Como se mencionó anteriormente, si\(f\) tiene un extremo local en un punto\(x=c\), entonces\(c\) debe ser un punto crítico de\(f\). Este hecho se conoce como teorema de Fermat.

Teorema\(\PageIndex{2}\): Fermat’s Theorem

Si\(f\) tiene un extremo local en\(c\) y\(f\) es diferenciable en\(c\), entonces\(f'(c)=0.\)

Prueba

Supongamos que\(f\) tiene un extremo local en\(c\) y\(f\) es diferenciable en\(c\). Tenemos que demostrarlo\(f'(c)=0\). Para ello, vamos a demostrar eso\(f'(c)≥0\) y\(f'(c)≤0\), y por lo tanto\(f'(c)=0\). Ya que\(f\) tiene un extremo local en\(c\),\(f\) tiene un máximo local o mínimo local en\(c\). Supongamos que\(f\) tiene un máximo local en\(c\). El caso en el que\(f\) tiene un mínimo local en se\(c\) puede manejar de manera similar. Ahí existe entonces un intervalo abierto I tal que\(f(c)≥f(x)\) para todos\(x∈I\). Ya que\(f\) es diferenciable en\(c\), a partir de la definición de la derivada, sabemos que

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Dado que este límite existe, ambos límites unilaterales también existen e iguales\(f'(c)\). Por lo tanto,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2} \]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Ya que\(f(c)\) es un máximo local, vemos que\(f(x)−f(c)≤0\) por\(x\) cerca\(c\). Por lo tanto\(c\), por\(x\) cerca\(x>c\), pero, tenemos\(\frac{f(x)−f(c)}{x−c}≤0\). De la Ecuación\ ref {FermateQN2} concluimos que\(f'(c)≤0\). De igual manera, puede demostrarse que\(f'(c)≥0.\) Por lo tanto,\(f'(c)=0.\)

□

Del teorema de Fermat, concluimos que si\(f\) tiene un extremo local en\(c\), entonces cualquiera\(f'(c)=0\) o\(f'(c)\) es indefinido. En otras palabras, los extremos locales solo pueden ocurrir en puntos críticos.

Tenga en cuenta que este teorema no afirma que una función\(f\) deba tener un extremo local en un punto crítico. Más bien, afirma que los puntos críticos son candidatos a los extremos locales. Por ejemplo, considere la función\(f(x)=x^3\). Tenemos\(f'(x)=3x^2=0\) cuando\(x=0\). Por lo tanto,\(x=0\) es un punto crítico. Sin embargo,\(f(x)=x^3\) está aumentando sobre\((−∞,∞)\), y por lo tanto\(f\) no tiene un extremo local en\(x=0\). En la Figura\(\PageIndex{4}\), vemos varias posibilidades diferentes para los puntos críticos. En algunos de estos casos, las funciones tienen extremos locales en puntos críticos, mientras que en otros casos las funciones no. Tenga en cuenta que estas gráficas no muestran todas las posibilidades para el comportamiento de una función en un punto crítico.

Esta figura tiene cinco partes a, b, c, d y e. En la figura a, se muestra una parábola hacia abajo en el cuadrante I; hay una línea tangente horizontal en el máximo local marcada con f' (c) = 0. En la figura b, hay una función dibujada con una asíntota en c, lo que significa que la función aumenta hacia el infinito en ambos lados de c; se observa que f' (c) no está definido. En la figura c, se muestra una versión de la gráfica de valores absolutos que ha sido desplazada para que su mínimo esté en el cuadrante I con x = c. Se observa que f' (c) es indefinido. En la figura d, se muestra una versión de la función f (x) = x^3 que ha sido desplazada para que su punto de inflexión esté en el cuadrante I con x = c. Su punto de inflexión en (c, f (c)) tiene una línea horizontal a través del mismo, y se observa que f' (c) = 0. En la figura e, se muestra una versión de la función f (x) = x1/3 que ha sido desplazada para que su punto de inflexión esté en el cuadrante I con x = c. Su punto de inflexión en (c, f (c)) tiene una línea vertical a través del mismo, y se observa que f' (c) es indefinido. — Figura\(\PageIndex{4}\): (a—e) Una función\(f\) tiene un punto crítico en\(c\) si\(f'(c)=0\) o\(f'(c)\) es indefinida. Una función puede tener o no un extremo local en un punto crítico.

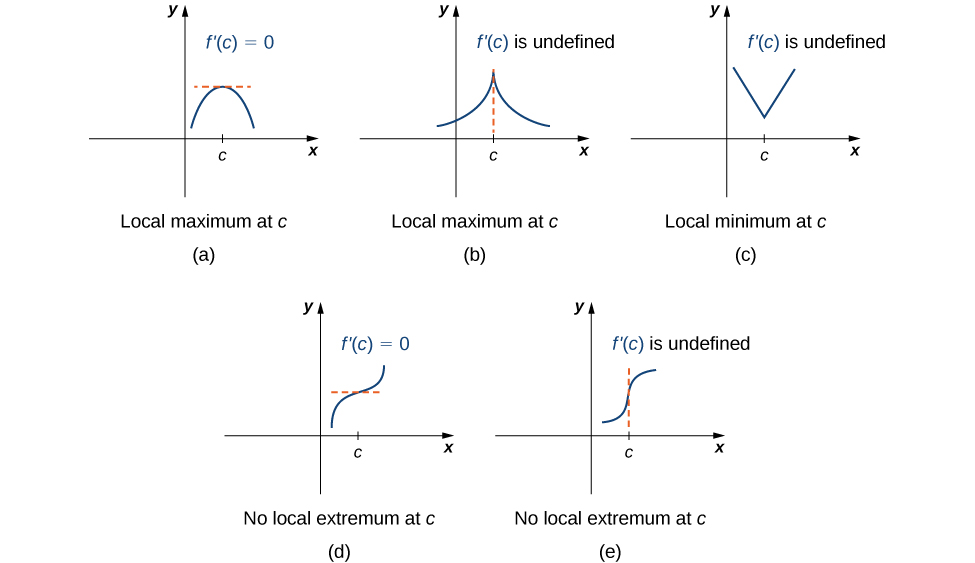
Más adelante en este capítulo analizamos métodos analíticos para determinar si una función realmente tiene un extremo local en un punto crítico. Por ahora, volvamos nuestra atención a encontrar puntos críticos. Utilizaremos observaciones gráficas para determinar si un punto crítico está asociado con un extremo local.

Ejemplo\(\PageIndex{1}\): Locating Critical Points

Para cada una de las siguientes funciones, encuentra todos los puntos críticos. Utilice una utilidad gráfica para determinar si la función tiene un extremo local en cada uno de los puntos críticos.

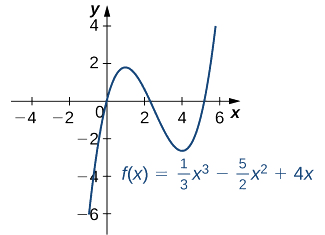
\(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
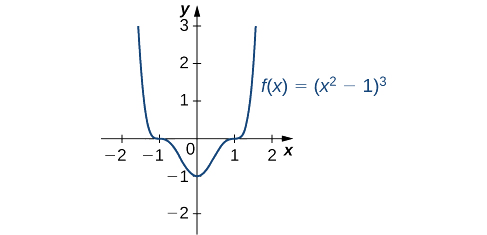
\(f(x)=(x^2−1)^3\)
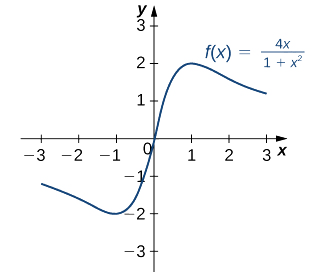
\(f(x)=\frac{4x}{1+x^2}\)

Solución

a. La derivada\(f'(x)=x^2−5x+4\) se define para todos los números reales\(x\). Por lo tanto, solo necesitamos encontrar los valores para\(x\) dónde\(f'(x)=0\). Ya que\(f'(x)=x^2−5x+4=(x−4)(x−1)\), los puntos críticos son\(x=1\) y\(x=4.\) A partir de la gráfica de\(f\) en Figura\(\PageIndex{5}\), vemos que\(f\) tiene un máximo local en\(x=1\) y un mínimo local en\(x=4\).

Se grafica la función f (x) = (1/3) x^3 — (5/2) x^2 + 4x. La función tiene máximo local en x = 1 y mínimo local en x = 4. — Figura\(\PageIndex{5}\): Esta función tiene un máximo local y un mínimo local.

b. Usando la regla de la cadena, vemos que la derivada es

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

Por lo tanto,\(f\) tiene puntos críticos cuándo\(x=0\) y cuándo\(x^2−1=0\). Se concluye que los puntos críticos son\(x=0,±1\). De la gráfica de\(f\) en Figura\(\PageIndex{6}\), vemos que\(f\) tiene un mínimo local (y absoluto) en\(x=0\), pero no tiene un extremo local en\(x=1\) o\(x=−1\).

Se grafica la función f (x) = (x^2 − 1) 3. La función tiene mínimo local en x = 0, y puntos de inflexión en x = ±1. — Figura\(\PageIndex{6}\): Esta función tiene tres puntos críticos:\(x=0\),\(x=1\), y\(x=−1\). La función tiene un mínimo local (y absoluto) en\(x=0\), pero no tiene extremos en los otros dos puntos críticos.

c. Por la regla del cociente, vemos que la derivada es

\(f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

El derivado se define en todas partes. Por lo tanto, solo necesitamos encontrar valores para\(x\) dónde\(f'(x)=0\). Resolviendo\(f'(x)=0\), vemos aquello\(4−4x^2=0,\) que implica\(x=±1\). Por lo tanto, los puntos críticos son\(x=±1\). De la gráfica de\(f\) en la Figura\(\PageIndex{7}\), vemos que f tiene un máximo absoluto en\(x=1\) y un mínimo absoluto en\(x=−1.\) Por lo tanto,\(f\) tiene un máximo local en\(x=1\) y un mínimo local en\(x=−1\). (Tenga en cuenta que si\(f\) tiene un extremo absoluto sobre un intervalo\(I\) en un punto\(c\) que no es un punto final de\(I\), entonces\(f\) tiene un extremo local en\(c.)\)

Se grafica la función f (x) = 4x/ (1 + x^2). La función tiene máximo local/absoluto en x = 1 y mínimo local/absoluto en x = −1. — Figura\(\PageIndex{7}\): Esta función tiene un máximo absoluto y un mínimo absoluto.

Ejercicio\(\PageIndex{1}\)

Encuentra todos los puntos críticos para\(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Pista: Calcular\(f'(x).\)

Contestar: \(x=\frac{−2}{3}, x=1\)

Localizando Extrema Absoluta

El teorema del valor extremo establece que una función continua sobre un intervalo cerrado y delimitado tiene un máximo absoluto y un mínimo absoluto. Como se muestra en la Figura\(\PageIndex{2}\), uno o ambos de estos extremos absolutos podrían ocurrir en un punto final. Si un extremo absoluto no ocurre en un punto final, sin embargo, debe ocurrir en un punto interior, en cuyo caso el extremo absoluto es un extremo local. Por lo tanto, según el Teorema de Fermat, el punto\(c\) en el que ocurre el extremo local debe ser un punto crítico. Resumimos este resultado en el siguiente teorema.

Teorema\(\PageIndex{3}\): Location of Absolute Extrema

Let\(f\) Ser una función continua sobre un intervalo cerrado y delimitado\(I\). El máximo absoluto de\(f\) más\(I\) y el mínimo absoluto de\(f\) más\(I\) deben ocurrir en puntos finales de\(I\) o en puntos críticos de\(f\) in\(I\).

Con esta idea en mente, examinemos un procedimiento para localizar los extremos absolutos.

Estrategia de Resolución de Problemas: Localización de Extremos Absolutos en Intervalo Cerrado

Considerar una función continua\(f\) definida en el intervalo cerrado\([a,b].\)

Evaluar\(f\) en los puntos finales\(x=a\) y\(x=b.\)
Encontrar todos los puntos críticos de\(f\) que se encuentran en el intervalo\((a,b)\) y evaluar\(f\) en esos puntos críticos.
Compare todos los valores encontrados en (1) y (2). Desde “Ubicación de Extrema Absoluta”, los extremos absolutos deben ocurrir en puntos finales o puntos críticos. Por lo tanto, el mayor de estos valores es el máximo absoluto de\(f\). El más pequeño de estos valores es el mínimo absoluto de\(f\).

Ahora veamos cómo usar esta estrategia para encontrar los valores máximos absolutos y mínimos absolutos para funciones continuas.

Ejemplo\(\PageIndex{2}\): Locating Absolute Extrema

Para cada una de las siguientes funciones, encuentre el máximo absoluto y el mínimo absoluto durante el intervalo especificado y indique dónde ocurren esos valores.

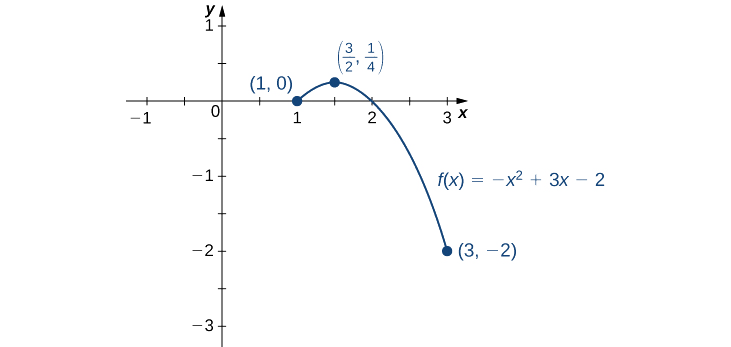
\(f(x)=−x^2+3x−2\)sobre\([1,3].\)
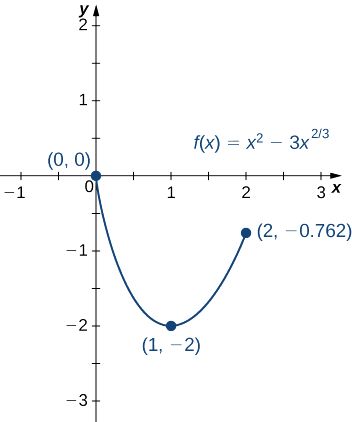
\(f(x)=x^2−3x^{2/3}\)terminado\([0,2]\).

Solución

a. Paso 1. Evaluar\(f\) en los puntos finales\(x=1\) y\(x=3\).

\(f(1)=0\)y\(f(3)=−2\)

Paso 2. Ya que\(f'(x)=−2x+3, f'\) se define para todos los números reales\(x.\) Por lo tanto, no hay puntos críticos donde la derivada esté indefinida. Queda por comprobar dónde\(f'(x)=0\). Dado que\(f'(x)=−2x+3=0 \) at\(x=\frac{3}{2}\) y\(\frac{3}{2}\) está en el intervalo\([1,3], f(\frac{3}{2})\) es un candidato para un extremo absoluto de\(f\) más\([1,3]\). Evaluamos\(f(\frac{3}{2})\) y encontramos

\(f\left(\frac{3}{2}\right)=\frac{1}{4}\).

Paso 3. Se configuró la siguiente tabla para comparar los valores encontrados en los pasos 1 y 2.

\(x\)	\(f(x)\)	Conclusión
\(1\)	\(0\)
\(\frac{3}{2}\)	\(\frac{1}{4}\)	Máximo absoluto
\(3\)	\(−2\)	Mínimo absoluto

De la tabla, encontramos que el máximo absoluto de\(f\) sobre el intervalo [1, 3] es\(\frac{1}{4}\), y ocurre en\(x=\frac{3}{2}\). El mínimo absoluto de\(f\) sobre el intervalo\([1, 3]\) es\(−2\), y ocurre en\(x=3\) como se muestra en la Figura\(\PageIndex{8}\).

La función f (x) = — x^2 + 3x — 2 se grafica de (1, 0) a (3, −2), con su máximo marcado en (3/2, 1/4). — Figura\(\PageIndex{8}\): Esta función tiene tanto un máximo absoluto como un mínimo absoluto.

b. Paso 1. Evaluar\(f\) en los puntos finales\(x=0\) y\(x=2\).

\(f(0)=0\)y\(f(2)=4−3\left(2\right)^{2/3}≈−0.762\)

Paso 2. La derivada de\(f\) viene dada por

\(f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}\)

para\(x≠0\). La derivada es cero cuando\(2x^{4/3}−2=0\), lo que implica\(x=±1\). La derivada está indefinida en\(x=0\). Por lo tanto, los puntos críticos de\(f\) son\(x=0,1,−1\). El punto\(x=0\) es un punto final, por lo que ya evaluamos\(f(0)\) en el paso 1. El punto no\(x=−1\) está en el intervalo de interés, por lo que sólo necesitamos evaluar\(f(1)\). Nos encontramos con que

\(f(1)=−2.\)

Paso 3. Comparamos los valores encontrados en los pasos 1 y 2, en la siguiente tabla.

\(x\)	\(f(x)\)	Conclusión
\(0\)	\(0\)	Máximo absoluto
\(1\)	\(−2\)	Mínimo absoluto
\(2\)	\(−0.762\)

Concluimos que el máximo absoluto de\(f\) sobre el intervalo\([0, 2]\) es cero, y ocurre en\(x=0\). El mínimo absoluto es\(−2,\) y ocurre en\(x=1\) como se muestra en la Figura\(\PageIndex{9}\).

La función f (x) = x^2 — 3x^ (2/3) se grafica de (0, 0) a (2, −0.762), con su mínimo marcado en (1, −2). — Figura\(\PageIndex{9}\): Esta función tiene un máximo absoluto en un punto final del intervalo.

Ejercicio\(\PageIndex{2}\)

Encuentra el máximo absoluto y el mínimo absoluto de\(f(x)=x^2−4x+3\) sobre el intervalo\([1,4]\).

Pista: Busque puntos críticos. Evaluar\(f\) en todos los puntos críticos y en los puntos finales.

Contestar: El máximo absoluto es\(3\) y ocurre en\(x=4\). El mínimo absoluto es\(−1\) y ocurre en\(x=2\).

En este punto, sabemos cómo ubicar los extremos absolutos para funciones continuas en intervalos cerrados. También hemos definido extremos locales y determinado que si una función\(f\) tiene un extremo local en un punto\(c\), entonces\(c\) debe ser un punto crítico de\(f\). Sin embargo,\(c\) ser un punto crítico no es una condición suficiente\(f\) para tener un extremo local en\(c\). Más adelante en este capítulo, mostramos cómo determinar si una función realmente tiene un extremo local en un punto crítico. Primero, sin embargo, necesitamos introducir el Teorema del Valor Medio, que nos ayudará a analizar el comportamiento de la gráfica de una función.

Conceptos clave

Una función puede tener tanto un máximo absoluto como un mínimo absoluto, tener solo un extremo absoluto, o no tener un máximo absoluto o mínimo absoluto.
Si una función tiene un extremo local, el punto en el que ocurre debe ser un punto crítico. Sin embargo, una función no necesita tener un extremo local en un punto crítico.
Una función continua sobre un intervalo cerrado y delimitado tiene un máximo absoluto y un mínimo absoluto. Cada extremo ocurre en un punto crítico o un punto final.

Glosario

extremo absoluto: si\(f\) tiene un máximo absoluto o un mínimo absoluto en\(c\), decimos que\(f\) tiene un extremo absoluto en\(c\)

máximo absoluto: si\(f(c)≥f(x)\) para todos\(x\) en el dominio de\(f\), decimos que\(f\) tiene un máximo absoluto en\(c\)

mínimo absoluto: si\(f(c)≤f(x)\) para todos\(x\) en el dominio de\(f\), decimos que\(f\) tiene un mínimo absoluto en\(c\)

punto crítico: si\(f'(c)=0\) o\(f'(c)\) es indefinido, decimos que c es un punto crítico de\(f\)

Teorema del valor extremo: si\(f\) es una función continua sobre un intervalo finito cerrado, entonces\(f\) tiene un máximo absoluto y un mínimo absoluto

Teorema de Fermat: si\(f\) tiene un extremo local en\(c\), entonces\(c\) es un punto crítico de\(f\)

extremo local: si\(f\) tiene un máximo local o mínimo local en\(c\), decimos que\(f\) tiene un extremo local en\(c\)

máximo local: si existe un intervalo\(I\) tal que\(f(c)≥f(x)\) para todos\(x∈I\), decimos\(f\) tiene un máximo local en\(c\)

mínimo local: si existe un intervalo\(I\) tal que\(f(c)≤f(x)\) para todos\(x∈I\), decimos que\(f\) tiene un mínimo local en\(c\)

Search

Text Color

Text Size

Margin Size

Font Type