4.4: El teorema del valor medio

Última actualización
Guardar como PDF

Page ID: 116509

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Explicar el significado del teorema de Rolle.
Describir la significancia del Teorema del Valor Medio.
Anotar tres consecuencias importantes del Teorema del Valor Medio.

El Teorema del Valor Medio es uno de los teoremas más importantes en el cálculo. Analizamos algunas de sus implicaciones al final de esta sección. Primero, comencemos con un caso especial del Teorema del Valor Medio, llamado teorema de Rolle.

Teorema de Rolle

Informalmente, el teorema de Rolle establece que si las salidas de una función diferenciable$f$ son iguales en los puntos finales de un intervalo, entonces debe haber un punto interior$c$ donde$f'(c)=0$. La figura$\PageIndex{1}$ ilustra este teorema.

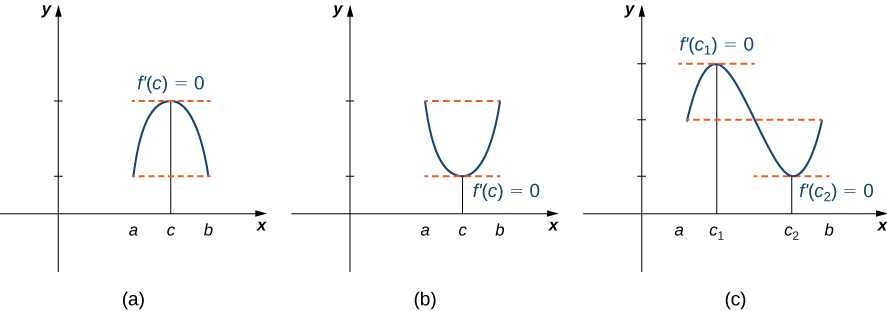
La figura se divide en tres partes etiquetadas a, b y c. La figura a muestra el primer cuadrante con los valores a, c y b marcados en el eje x. Se dibuja una parábola orientada hacia abajo de tal manera que sus valores en a y b son los mismos. El punto c es el máximo global, y se observa que f' (c) = 0. La Figura b muestra el primer cuadrante con los valores a, c y b marcados en el eje x. Se dibuja una parábola orientada hacia arriba de tal manera que sus valores en a y b son los mismos. El punto c es el mínimo global, y se observa que f' (c) = 0. La figura c muestra el primer cuadrante con los puntos a, c1, c2 y b marcados en el eje x. Se dibuja un periodo de una onda sinusoidal de tal manera que sus valores en a y b son iguales. El punto c1 es el máximo global, y se observa que f' (c1) = 0. El punto c2 es el mínimo global, y se observa que f' (c2) = 0. — Figura$\PageIndex{1}$: Si una función diferenciable$f$ satisface$f(a)=f(b)$, entonces su derivada debe ser cero en algún punto (s) entre$a$ y$b$.

Teorema de Rolle

Dejar$f$ ser una función continua sobre el intervalo cerrado$[a,b]$ y diferenciable sobre el intervalo abierto$(a,b)$ tal que$f(a)=f(b)$. Entonces existe al menos uno$c∈(a,b)$ tal que$f'(c)=0.$

Prueba

Vamos$k=f(a)=f(b).$ Consideramos tres casos:

$f(x)=k$para todos$x∈(a,b).$
Existe$x∈(a,b)$ tal que$f(x)>k.$
Existe$x∈(a,b)$ tal que$f(x)<k.$

Caso 1: Si es$f(x)=k$ para todos$x∈(a,b)$, entonces$f'(x)=0$ para todos$x∈(a,b).$

Caso 2: Dado que$f$ es una función continua sobre el intervalo cerrado, acotado$[a,b]$, por el teorema del valor extremo, tiene un máximo absoluto. También, ya que hay un punto$x∈(a,b)$ tal que$f(x)>k$, el máximo absoluto es mayor que$k$. Por lo tanto, el máximo absoluto no ocurre en ninguno de los dos extremos. En consecuencia, el máximo absoluto debe ocurrir en un punto interior$c∈(a,b)$. Porque$f$ tiene un máximo en un punto interior$c$, y$f$ es diferenciable en$c$, según el teorema de Fermat,$f'(c)=0.$

Caso 3: El caso cuando exista un punto$x∈(a,b)$ tal que$f(x)<k$ sea análogo al caso 2, con máximo sustituido por mínimo.

□

Un punto importante sobre el teorema de Rolle es que la diferenciabilidad de la función$f$ es crítica. Si no$f$ es diferenciable, incluso en un solo punto, es posible que el resultado no se mantenga. Por ejemplo, la función$f(x)=|x|−1$ es continua sobre$[−1,1]$ y$f(−1)=0=f(1)$, pero$f'(c)≠0$ para cualquiera$c∈(−1,1)$ como se muestra en la siguiente figura.

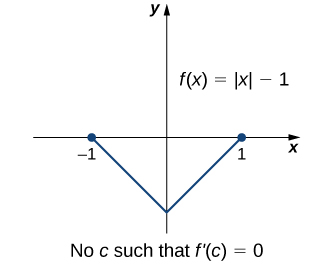
Se grafica la función f (x) = |x| − 1. Se muestra que f (1) = f (−1), pero se observa que no hay c tal que f' (c) = 0. — Figura$\PageIndex{2}$: Dado que no$f(x)=|x|−1$ es diferenciable en$x=0$, no se satisfacen las condiciones del teorema de Rolle. De hecho, la conclusión no se sostiene aquí; no hay$c∈(−1,1)$ tal que$f'(c)=0.$

Consideremos ahora las funciones que satisfacen las condiciones del teorema de Rolle y calculemos explícitamente los puntos$c$ donde$f'(c)=0.$

Ejemplo$\PageIndex{1}$: Using Rolle’s Theorem

Para cada una de las siguientes funciones, verificar que la función cumpla con los criterios establecidos en el teorema de Rolle y encuentre todos los valores$c$ en el intervalo dado donde$f'(c)=0.$

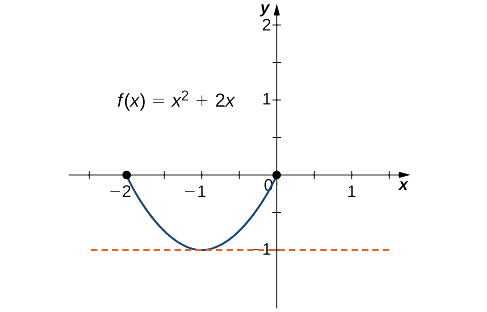
$f(x)=x^2+2x$sobre$[−2,0]$
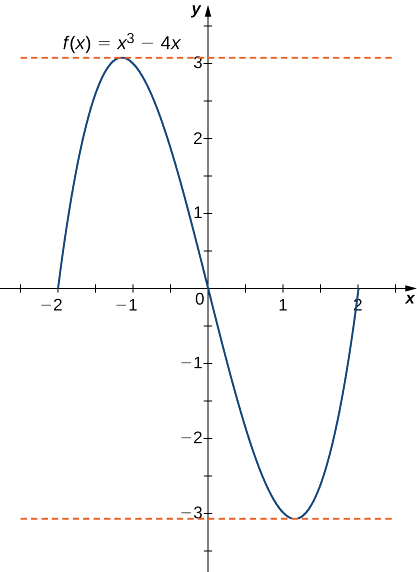
$f(x)=x^3−4x$sobre$[−2,2]$

Solución

a. ya que$f$ es un polinomio, es continuo y diferenciable en todas partes. Además,$f(−2)=0=f(0).$ Por lo tanto,$f$ satisface los criterios del teorema de Rolle. Concluimos que existe al menos un valor$c∈(−2,0)$ tal que$f'(c)=0$. Ya que$f'(x)=2x+2=2(x+1),$ vemos eso$f'(c)=2(c+1)=0$ implica$c=−1$ como se muestra en la siguiente gráfica.

Se grafica la función f (x) = x2 +2x. Se muestra que f (0) = f (−2), y una línea horizontal discontinua se dibuja en el mínimo absoluto en (−1, −1). — Figura$\PageIndex{3}$: Esta función es continua y diferenciable sobre [−2,0],$f'(c)=0$ cuando$c=−1$.

b. como en la parte a.$f$ es un polinomio y por lo tanto es continuo y diferenciable en todas partes. También,$f(−2)=0=f(2).$ Dicho esto,$f$ satisface los criterios del teorema de Rolle. Diferenciando, encontramos que$f'(x)=3x^2−4.$ Por lo tanto,$f'(c)=0$ cuando$x=±\frac{2}{\sqrt{3}}$. Ambos puntos están en el intervalo$[−2,2]$, y, por lo tanto, ambos puntos satisfacen la conclusión del teorema de Rolle como se muestra en la siguiente gráfica.

Se grafica la función f (x) = x3 — 4x. Es obvio que f (2) = f (−2) = f (0). Las líneas horizontales discontinuas se dibujan a x = ±2/raíz cuadrada de 3, que son el máximo y mínimo locales. — Figura$\PageIndex{4}$: Para este polinomio sobre$[−2,2], f'(c)=0$ at$x=±2/\sqrt{3}$.

Ejercicio$\PageIndex{1}$

Verificar que la función$f(x)=2x^2−8x+6$ definida a lo largo del intervalo$[1,3]$ satisfaga las condiciones del teorema de Rolle. Encuentra todos los puntos$c$ garantizados por el teorema de Rolle.

Pista: Encuentra todos los valores$c$, donde$f'(c)=0$.

Contestar: $c=2$

El teorema del valor medio y su significado

El teorema de Rolle es un caso especial del Teorema del Valor Medio. En el teorema de Rolle, consideramos funciones diferenciables$f$ que son cero en los puntos finales. El Teorema del Valor Medio generaliza el teorema de Rolle considerando funciones que no son necesariamente cero en los puntos finales. En consecuencia, podemos ver el Teorema del Valor Medio como una versión inclinada del teorema de Rolle (Figura$\PageIndex{5}$). El Teorema del Valor Medio establece que si$f$ es continuo sobre el intervalo cerrado$[a,b]$ y diferenciable sobre el intervalo abierto$(a,b)$, entonces existe un punto$c∈(a,b)$ tal que la línea tangente a la gráfica de$f$ at$c$ es paralela a la línea secante que conecta $(a,f(a))$y$(b,f(b)).$

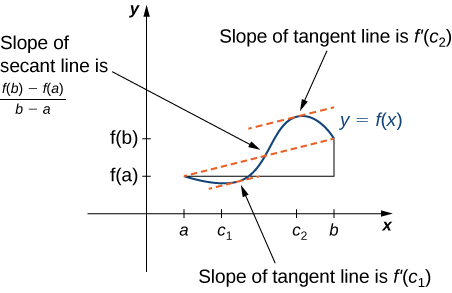
Se dibuja una función vagamente sinusoidal y = f (x). En el eje x, se marcan a, c1, c2 y b. En el eje y se marcan f (a) y f (b). La función f (x) comienza en (a, f (a)), disminuye a c1, aumenta a c2, y luego disminuye a (b, f (b)). Se dibuja una línea secante entre (a, f (a)) y (b, f (b)), y se observa que esta línea tiene pendiente (f (b) — f (a))/(b − a). Se dibujan las líneas tangentes en c1 y c2, y estas líneas son paralelas a la línea secante. Se observa que las pendientes de estas líneas tangentes son f' (c1) y f' (c2), respectivamente. — Figura$\PageIndex{5}$: El Teorema del Valor Medio dice que para una función que cumple con sus condiciones, en algún momento la línea tangente tiene la misma pendiente que la línea secante entre los extremos. Para esta función, hay dos valores$c_1$ y$c_2$ tales que la línea tangente a$f$ at$c_1$ y$c_2$ tiene la misma pendiente que la línea secante.

Teorema del valor medio

Dejar$f$ ser continuo sobre el intervalo cerrado$[a,b]$ y diferenciable sobre el intervalo abierto$(a,b)$. Entonces, existe al menos un punto$c∈(a,b)$ tal que

\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]

Prueba

La prueba se desprende del teorema de Rolle al introducir una función apropiada que satisface los criterios del teorema de Rolle. Considera la línea de conexión$(a,f(a))$ y$(b,f(b)).$ Dado que la pendiente de esa línea es

\[\frac{f(b)−f(a)}{b−a} \nonumber \]

y la línea pasa por el punto$(a,f(a)),$ la ecuación de esa línea puede escribirse como

\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]

Dejar$g(x)$ denotar la diferencia vertical entre el punto$(x,f(x))$ y el punto$(x,y)$ en esa línea. Por lo tanto,

\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]

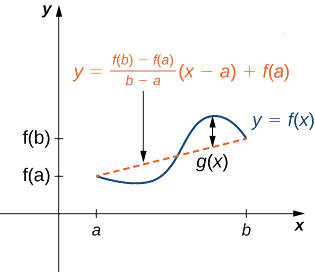$Curva ascendente pero oscilante Y es igual a F de X con la línea secante Y es igual a F de B menos F de A en todo B menos A más F de A, la distancia entre la curva oscilante y la línea es G de X$ Figura$\PageIndex{6}$: El valor$g(x)$ es la diferencia vertical entre el punto$(x,f(x))$ y el punto$(x,y)$ en la línea secante que conecta$(a,f(a))$ y$(b,f(b))$.

Ya que la gráfica de$f$ cruza la línea secante cuando$x=a$ y$x=b$, vemos eso$g(a)=0=g(b)$. Dado que$f$ es una función diferenciable sobre$(a,b)$, también$g$ es una función diferenciable sobre$(a,b)$. Además, dado que$f$ es continuo sobre también$[a,b], \, g$ es continuo sobre$[a,b]$. Por lo tanto,$g$ satisface los criterios del teorema de Rolle. En consecuencia, existe un punto$c∈(a,b)$ tal que$g'(c)=0.$ Desde

\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]

vemos que

\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]

Desde que$g'(c)=0,$ concluimos que

\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

□

En el siguiente ejemplo, mostramos cómo se puede aplicar el Teorema del Valor Medio a la función a$f(x)=\sqrt{x}$ lo largo del intervalo$[0,9]$. El método es el mismo para otras funciones, aunque a veces con consecuencias más interesantes.

Ejemplo$\PageIndex{2}$: Verifying that the Mean Value Theorem Applies

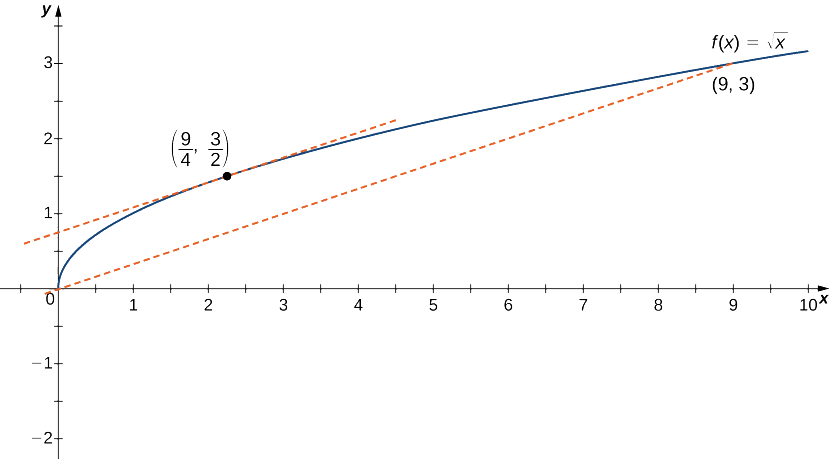
Para$f(x)=\sqrt{x}$ sobre el intervalo$[0,9]$, mostrar que$f$ satisface la hipótesis del Teorema del Valor Medio, y por lo tanto existe al menos un valor$c∈(0,9)$ tal que$f′(c)$ es igual a la pendiente de la línea que conecta$(0,f(0))$ y$(9,f(9))$. Encuentra estos valores$c$ garantizados por el Teorema del Valor Medio.

Solución

Sabemos que$f(x)=\sqrt{x}$ es continuo sobre$[0,9]$ y diferenciable sobre$(0,9).$ Por lo tanto,$f$ satisface las hipótesis del Teorema del Valor Medio, y debe existir al menos un valor$c∈(0,9)$ tal que$f′(c)$ sea igual a la pendiente de la línea de conexión$(0,f(0))$ y$(9,f(9))$ (Figura$\PageIndex{7}$). Para determinar qué valor (s) de$c$ están garantizados, primero calcule la derivada de$f$. El derivado$f′(x)=\frac{1}{(2\sqrt{x})}$. La pendiente de la línea que conecta$(0,f(0))$ y$(9,f(9))$ viene dada por

\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]

Queremos encontrar$c$ tal que$f′(c)=\frac{1}{3}$. Es decir, queremos encontrar$c$ tal que

\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]

Resolviendo esta ecuación para$c$, obtenemos$c=\frac{9}{4}$. En este punto, la pendiente de la línea tangente es igual a la pendiente de la línea que une los puntos finales.

La función f (x) = la raíz cuadrada de x se grafica de (0, 0) a (9, 3). Hay una línea secante dibujada de (0, 0) a (9, 3). En el punto (9/4, 3/2), hay una línea tangente que se dibuja, y esta línea es paralela a la línea secante. — Figura$\PageIndex{7}$: La pendiente de la línea tangente en$c=9/4$ es la misma que la pendiente del segmento de línea que conecta (0,0) y (9,3).

Una aplicación que ayuda a ilustrar el Teorema del Valor Medio involucra la velocidad. Por ejemplo, supongamos que conducimos un automóvil durante 1 h por una carretera recta con una velocidad promedio de 45 mph. Dejar$s(t)$ y$v(t)$ denotar la posición y velocidad del carro, respectivamente, para$0≤t≤1$ h. Suponiendo que la función de posición$s(t)$ es diferenciable, podemos aplicar el Teorema del Valor Medio para concluir que, en algún momento$c∈(0,1)$, la velocidad del carro era exactamente

\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]

Ejemplo$\PageIndex{3}$: Mean Value Theorem and Velocity

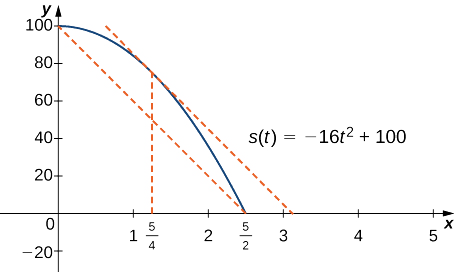
Si una roca cae desde una altura de 100 pies, su posición$t$ segundos después de que se caiga hasta que golpee el suelo viene dada por la función$s(t)=−16t^2+100.$

Determina cuánto tiempo tarda en que la roca golpee el suelo.
Encuentra la velocidad promedio$v_{avg}$ de la roca para cuando la roca se libera y la roca golpea el suelo.
Encuentra el tiempo$t$ garantizado por el Teorema del Valor Medio cuando la velocidad instantánea de la roca es$v_{avg}.$

Solución

a. Cuando la roca choca contra el suelo, su posición es$s(t)=0$. Resolviendo la ecuación$−16t^2+100=0$ para$t$, nos encontramos con eso$t=±\frac{5}{2}sec$. Ya que solo estamos considerando$t≥0$, la pelota golpeará el suelo$\frac{5}{2}$ seg después de que se le haya caído.

b. La velocidad promedio viene dada por

\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]

c. La velocidad instantánea viene dada por la derivada de la función de posición. Por lo tanto, necesitamos encontrar un tiempo$t$ tal que$v(t)=s′(t)=v_{avg}=−40$ pies/seg. Dado que$s(t)$ es continuo a lo largo del intervalo$[0,5/2]$ y diferenciable en el intervalo$(0,5/2),$ por el Teorema del Valor Medio, se garantiza que haya un punto$c∈(0,5/2)$ tal que

\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]

Tomando la derivada de la función de posición$s(t)$, encontramos que$s′(t)=−32t.$ Por lo tanto, la ecuación se reduce a$s′(c)=−32c=−40.$ Resolver esta ecuación para$c$, tenemos$c=\frac{5}{4}$. Por lo tanto,$\frac{5}{4}$ segundos después de la caída de la roca, la velocidad instantánea es igual a la velocidad promedio de la roca durante su caída libre:$−40$ pies/seg.

La función s (t) = −16t2 + 100 se grafica de (0, 100) a (5/2, 0). Hay una línea secante dibujada de (0, 100) a (5/2, 0). En el punto correspondiente a x = 5/4, hay una línea tangente que se dibuja, y esta línea es paralela a la línea secante. — Figura$\PageIndex{8}$: En el tiempo$t=5/4$ seg, la velocidad de la roca es igual a su velocidad promedio desde el momento en que cae hasta que golpea el suelo.

Ejercicio$\PageIndex{2}$

Supongamos que se cae una pelota desde una altura de 200 pies. Su posición en el momento$t$ es$s(t)=−16t^2+200.$ Encontrar el$t$ momento en que la velocidad instantánea de la pelota es igual a su velocidad promedio.

Pista: Primero, determina cuánto tiempo tarda la pelota en golpear el suelo. Después, encuentra la velocidad promedio de la pelota desde el momento en que se deja caer hasta que golpea el suelo.

Contestar: $\frac{5}{2\sqrt{2}}$sec

Corolarios del Teorema del Valor Medio

Veamos ahora tres corolarios del Teorema del Valor Medio. Estos resultados tienen consecuencias importantes, que utilizamos en próximas secciones.

En este punto, sabemos que la derivada de cualquier función constante es cero. El Teorema del Valor Medio nos permite concluir que lo contrario también es cierto. En particular, si$f′(x)=0$ para todos$x$ en algún intervalo$I$, entonces$f(x)$ es constante sobre ese intervalo. Este resultado puede parecer intuitivamente obvio, pero tiene implicaciones importantes que no son obvias, y las discutimos en breve.

Corolario 1: Funciones con una Derivada de Cero

Dejar$f$ ser diferenciable a lo largo de un intervalo$I$. Si$f′(x)=0$ por todos$x∈I$, entonces$f(x)=$ constante para todos$x∈I.$

Prueba

Ya que$f$ es diferenciable sobre$I$,$f$ debe ser continuo sobre$I$. Supongamos que no$f(x)$ es constante para todos$x$ en$I$. Luego existen$a,b∈I$, donde$a≠b$ y$f(a)≠f(b).$ Escoja la notación para que$a<b.$ Por lo tanto,

\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]

Dado que$f$ es una función diferenciable, por el Teorema del Valor Medio, existe$c∈(a,b)$ tal que

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Por lo tanto, existe$c∈I$ tal que$f′(c)≠0$, lo que contradice el supuesto de que$f′(x)=0$ para todos$x∈I$.

□

De “Corolario 1: Funciones con una Derivada de Cero”, se deduce que si dos funciones tienen la misma derivada, difieren en, como mucho, una constante.

Corolario 2: Teorema de Diferencia Constante

Si$f$ y$g$ son diferenciables a lo largo de un intervalo$I$ y$f′(x)=g′(x)$ para todos$x∈I$, entonces$f(x)=g(x)+C$ para alguna constante$C$.

Prueba

Deja$h(x)=f(x)−g(x).$ Entonces,$h′(x)=f′(x)−g′(x)=0$ para todos$x∈I.$ Por Corolario 1, hay una constante$C$ tal que$h(x)=C$ para todos$x∈I$. Por lo tanto,$f(x)=g(x)+C$ para todos$x∈I.$

□

El tercer corolario del Teorema del Valor Medio discute cuándo una función está aumentando y cuándo está disminuyendo. Recordemos que una función$f$ está aumentando sobre$I$ si$f(x_1)<f(x_2)$ siempre$x_1<x_2$, mientras que$f$ disminuye sobre$I$ si$f(x_1)>f(x_2)$ siempre$x_1<x_2$. Usando el Teorema del Valor Medio, podemos mostrar que si la derivada de una función es positiva, entonces la función está aumentando; si la derivada es negativa, entonces la función es decreciente (Figura$\PageIndex{9}$). Hacemos uso de este hecho en la siguiente sección, donde mostramos cómo usar la derivada de una función para localizar los valores locales máximos y mínimos de la función, y cómo determinar la forma de la gráfica.

Este hecho es importante porque significa que para una función dada$f$, si existe una función$F$ tal que$F′(x)=f(x)$; entonces, las únicas otras funciones que tienen una derivada igual a$f$ son$F(x)+C$ para alguna constante$C$. Discutimos este resultado con más detalle más adelante en el capítulo.

Se grafica una función vagamente sinusoidal f (x). Aumenta de algún lugar del segundo cuadrante a (a, f (a)). En esta sección se señala que f' — Figura$\PageIndex{9}$: Si una función tiene una derivada positiva durante algún intervalo$I$, entonces la función aumenta en ese intervalo$I$; si la derivada es negativa en algún intervalo$I$, entonces la función disminuye en ese intervalo$I$.

Corolario 3: Funciones crecientes y decrecientes

Dejar$f$ ser continuo sobre el intervalo cerrado$[a,b]$ y diferenciable sobre el intervalo abierto$(a,b)$.

Si$f′(x)>0$ para todos$x∈(a,b)$, entonces$f$ es una función creciente sobre$[a,b].$
Si$f′(x)<0$ para todos$x∈(a,b)$, entonces$f$ es una función decreciente sobre$[a,b].$

Prueba

Demostraremos i.; la prueba de ii. es similar. Supongamos que no$f$ es una función creciente en$I$. Entonces existen$a$ y$b$ en$I$ tal que$a<b$, pero$f(a)≥f(b)$. Dado que$f$ es una función diferenciable sobre$I$, por el Teorema del Valor Medio existe$c∈(a,b)$ tal que

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Ya que$f(a)≥f(b)$, eso lo sabemos$f(b)−f(a)≤0$. Además, nos$a<b$ dice que$b−a>0.$ Concluimos que

\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]

Sin embargo,$f′(x)>0$ para todos$x∈I$. Esto es una contradicción, y por lo tanto$f$ debe ser una función cada vez mayor$I$.

□

Conceptos clave

Si$f$ es continuo sobre$[a,b]$ y diferenciable sobre$(a,b)$ y$f(a)=f(b)$, entonces existe un punto$c∈(a,b)$ tal que$f′(c)=0.$ Este es el teorema de Rolle.
Si$f$ es continuo sobre$[a,b]$ y diferenciable sobre$(a,b)$, entonces existe un punto$c∈(a,b)$ tal que\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] Este es el Teorema del Valor Medio.
Si$f'(x)=0$ sobre un intervalo$I$, entonces$f$ es constante sobre$I$.
Si dos funciones diferenciables$f$ y$g$ satisfacer$f′(x)=g′(x)$ sobre$I$, entonces$f(x)=g(x)+C$ para alguna constante$C$.
Si$f′(x)>0$ sobre un intervalo$I$, entonces$f$ está aumentando sobre$I$. Si$f′(x)<0$ ha terminado$I$, entonces$f$ está disminuyendo sobre$I$.

Glosario

Teorema del valor medio: si$f$ es continuo sobre$[a,b]$ y diferenciable sobre$(a,b)$, entonces existe$c∈(a,b)$ tal que$f′(c)=\frac{f(b)−f(a)}{b−a}$

teorema de rolle: si$f$ es continuo sobre$[a,b]$ y diferenciable sobre$(a,b)$, y si$f(a)=f(b)$, entonces existe$c∈(a,b)$ tal que$f′(c)=0$