4.5E: Ejercicios para la Sección 4.5
( \newcommand{\kernel}{\mathrm{null}\,}\)
1) Sic es un punto crítico def(x), ¿cuándo no hay un máximo o mínimo local enc? Explique.
2) Para la funcióny=x3, ¿esx=0 tanto un punto de inflexión como un máximo/mínimo local?
- Contestar
- No es un máximo/mínimo local porquef′ no cambia signo
3) Para la funcióny=x3, ¿esx=0 un punto de inflexión?
4) ¿Es posible que un puntoc sea tanto un punto de inflexión como un extremo local de una función dos veces diferenciable?
- Contestar
- No
5) ¿Por qué necesitas continuidad para la primera prueba derivada? Vamos con un ejemplo.
6) Explicar si una función cóncava hacia abajo tiene que cruzary=0 por algún valor dex.
- Contestar
- Falso; por ejemplo,y=√x.
7) Explicar si un polinomio de grado2 puede tener un punto de inflexión.
En los ejercicios 8 - 12, analice las gráficas def′, luego enumere todos los intervalos dondef está aumentando o disminuyendo.
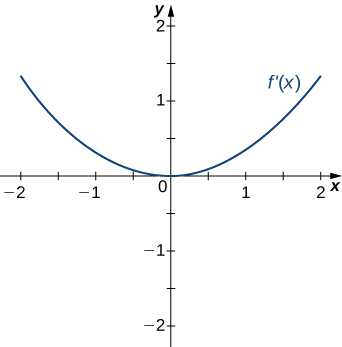
8)
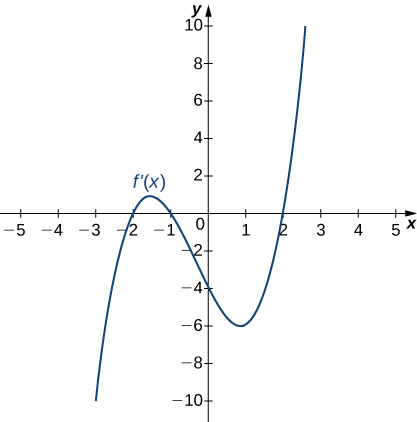
- Contestar
- Incrementando para−2<x<−1 yx>2;
Disminuyendo parax<−2 y−1<x<2
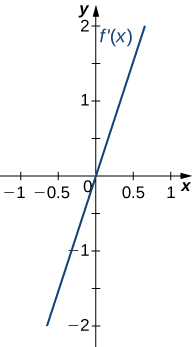
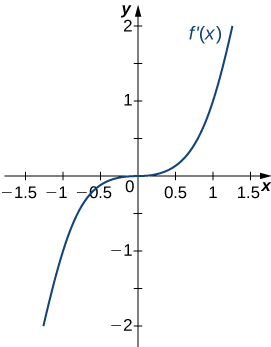
9)
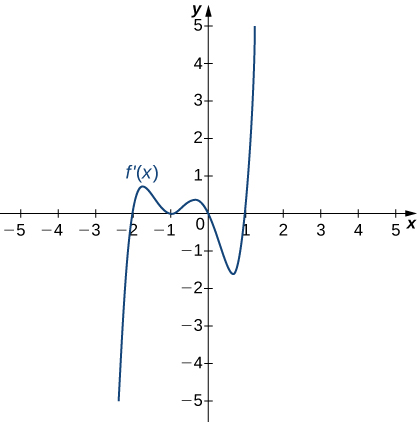
10)
- Contestar
- Disminuyendo parax<1,
Aumentando parax>1
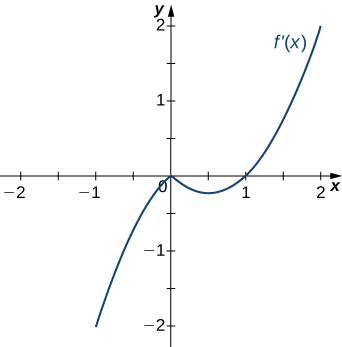
11)
12)
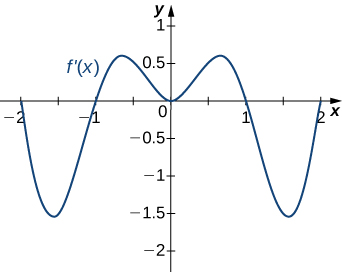
- Contestar
- Disminuyendo para−2<x<−1 y1<x<2;
Aumentando para−1<x<1 yx<−2 yx>2
En los ejercicios 13 - 17, analizar las gráficas def′, entonces enumerar todos los intervalos donde
a.f es creciente y decreciente y
b. se localizan los mínimos y máximos.
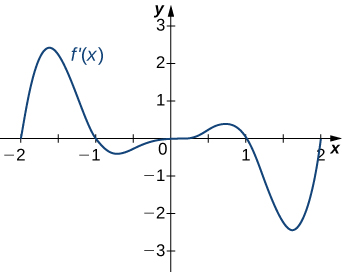
13)
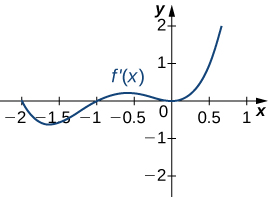
14)
- Contestar
- a. Aumentando sobre−2<x<−1,0<x<1,x>2, Disminuyendo sobrex<−2,−1<x<0,1<x<2;
b. Máximo enx=−1 yx=1, Mínimos enx=−2 yx=0 yx=2
15)
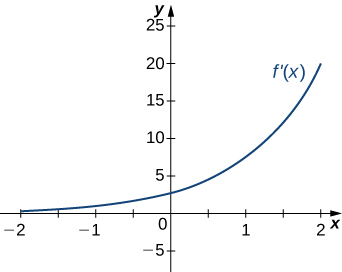
16)
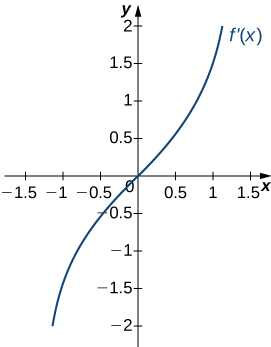
- Contestar
- a. Aumentando sobrex>0, disminuyendo sobrex<0;
b. Mínimo enx=0
17)
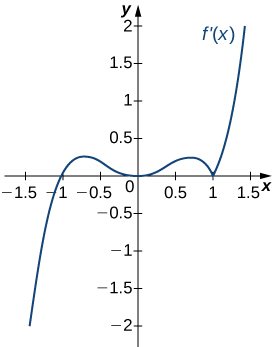
En los ejercicios 18 - 22, analice las gráficas def′, luego enumere todos los puntos e intervalosf de inflexión cóncavos hacia arriba y cóncavos hacia abajo.
18)
- Contestar
- Cóncavo para todosx,
sin puntos de inflexión
19)
20)
- Contestar
- Cóncavo para todosx,
sin puntos de inflexión
21)
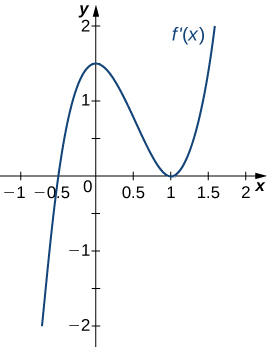
22)
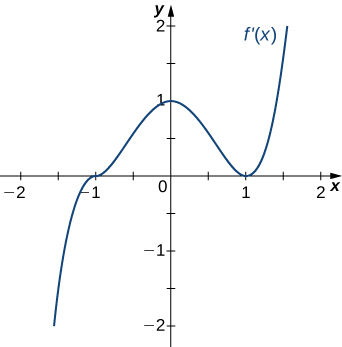
- Contestar
- Cóncavo hacia arriba parax<0 yx>1,
Cóncavo abajo para0<x<1, Puntos de
x=0 inflexiónx=1
Para los ejercicios 23 - 27, dibujar una gráfica que satisfaga las especificaciones dadas para el dominiox=[−3,3]. La función no tiene que ser continua o diferenciable.
23)f(x)>0,f′(x)>0x>1,−3<x<0,f′(x)=0 sobre0<x<1
24)f′(x)>0 sobrex>2,−3<x<−1,f′(x)<0 todo−1<x<2,f″ para todosx
- Contestar
- Las respuestas variarán
25)f''(x)<0 sobre el máximo−1<x<1,\;f''(x)>0,\;−3<x<−1,\;1<x<3,x=0, local en mínimos locales enx=±2
26) Hay un máximo local al mínimox=2, local enx=1, y la gráfica no es cóncava hacia arriba ni cóncava hacia abajo.
- Contestar
- Las respuestas variarán
27) Hay máximos locales enx=±1, la función es cóncava para todosx, y la función sigue siendo positiva para todosx.
Para los siguientes ejercicios, determine
a. intervalos dondef es creciente o decreciente y
b. mínimos locales y máximos def.
28)f(x)=\sin x+\sin^3x sobre−π<x<π
- Contestar
-
a. Aumentando por encima de−\frac{π}{2}<x<\frac{π}{2}, la disminuciónx<−\frac{π}{2},\; x>\frac{π}{2}
b. Máximo local enx=\frac{π}{2}; mínimo local enx=−\frac{π}{2}
29)f(x)=x^2+\cos x
Para el ejercicio 30, determinar
a. intervalos dondef es cóncavo hacia arriba o cóncavo hacia abajo, y
b. los puntos de inflexión def.
30)f(x)=x^3−4x^2+x+2
- Contestar
-
a. cóncavo hacia arriba parax>\frac{4}{3}, cóncavo hacia abajo parax<\frac{4}{3}
b. Punto de inflexiónx=\frac{4}{3}
Para los ejercicios 31 - 37, determinar
a. intervalos dondef está aumentando o disminuyendo,
b. mínimos y máximos locales def,
c. intervalos dondef es cóncavo hacia arriba y cóncavo hacia abajo, y
d. los puntos de inflexión def.
31)f(x)=x^2−6x
32)f(x)=x^3−6x^2
- Contestar
- a. Aumentandox<0 yx>4, disminuyendo sobre0<x<4
b. Máximo enx=0, mínimo enx=4
c. Cóncavo hacia arriba parax>2, cóncavo hacia abajo parax<2
d. Punto de inflexión enx=2
33)f(x)=x^4−6x^3
34)f(x)=x^{11}−6x^{10}
- Contestar
- a. Aumentando sobrex<0 yx>\frac{60}{11}, disminuyendo sobre0<x<\frac{60}{11}
b. Máximo enx=0, mínimo enx=\frac{60}{11}
c. Cóncavo hacia abajo parax<\frac{54}{11}, cóncavo hacia arriba parax>\frac{54}{11}
d. Punto de inflexión enx=\frac{54}{11}
35)f(x)=x+x^2−x^3
36)f(x)=x^2+x+1
- Contestar
- a. Aumentando sobrex>−\frac{1}{2}, disminuyendo sobrex<−\frac{1}{2}
b. Mínimo ax=−\frac{1}{2}
c. Cóncavo hacia arriba para todosx
d. Sin puntos de inflexión
37)f(x)=x^3+x^4
Para los ejercicios 38 - 47, determine
a. intervalos dondef está aumentando o disminuyendo,
b. mínimos y máximos locales def,
c. intervalos dondef es cóncavo hacia arriba y cóncavo hacia abajo, y
d. los puntos de inflexión def. Dibuje la curva, luego use una calculadora para comparar su respuesta. Si no puede determinar la respuesta exacta analíticamente, use una calculadora.
38) [T]f(x)=\sin(πx)−\cos(πx) sobrex=[−1,1]
- Contestar
- a. Aumenta sobre las−\frac{1}{4}<x<\frac{3}{4}, disminuciones sobrex>\frac{3}{4} yx<−\frac{1}{4}
b. Mínimo enx=−\frac{1}{4}, máximo enx=\frac{3}{4}
c. Cóncavo hacia arriba para−\frac{3}{4}<x<\frac{1}{4}, cóncavo hacia abajo parax<−\frac{3}{4} yx>\frac{1}{4}
d. Puntos de inflexión enx=−\frac{3}{4},\;x=\frac{1}{4}
39) [T]f(x)=x+\sin(2x) sobrex=[−\frac{π}{2},\frac{π}{2}]
40) [T]f(x)=\sin x+\tan x sobre(−\frac{π}{2},\frac{π}{2})
- Contestar
- a. Aumentando para todosx
b. No hay mínimo o máximo local
c. Cóncavo hacia arriba parax>0, cóncavo hacia abajo parax<0
d. Punto de inflexión enx=0
41) [T]f(x)=(x−2)^2(x−4)^2
42) [T]f(x)=\dfrac{1}{1−x},\quad x≠1
- Contestar
- a. Aumentando para todosx donde esté definido
b. No hay mínimos o máximos locales
c. Cóncavo hacia arriba parax<1; cóncavo hacia abajo parax>1
d. Sin puntos de inflexión en el dominio
43) [T]f(x)=\dfrac{\sin x}{x} sobrex=[-2π,0)∪(0,2π]
44)f(x)=\sin(x)e^x sobrex=[−π,π]
- Contestar
- a. Aumentando sobre−\frac{π}{4}<x<\frac{3π}{4}, disminuyendo sobrex>\frac{3π}{4},\;x<−\frac{π}{4}
b. Mínimo enx=−\frac{π}{4}, máximo enx=\frac{3π}{4}
c. Cóncavo hacia arriba para−\frac{π}{2}<x<\frac{π}{2}, cóncavo hacia abajo parax<−\frac{π}{2},\;x>\frac{π}{2}
d. Puntos de inflexión enx=±\frac{π}{2}
45)f(x)=\ln x\sqrt{x},\quad x>0
46)f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},\quad x>0
- Contestar
- a. Aumentando sobrex>4, disminuir sobre0<x<4
b. Mínimo ax=4
c. Cóncavo hacia arriba para0<x<8\sqrt[3]{2}, cóncavo hacia abajo parax>8\sqrt[3]{2}
d. Punto de inflexión enx=8\sqrt[3]{2}
47)f(x)=\dfrac{e^x}{x},\quad x≠0
En los ejercicios 48 - 52, interprete las oraciones en términos def,\;f', yf''.
48) La población crece más lentamente. Aquíf está la población.
- Contestar
- f>0,\;f'>0,\;f''<0
49) Una bicicleta acelera más rápido, pero un auto va más rápido. Aquí la posición de laf= bici menos la posición de Car.
50) El avión aterriza suavemente. Aquíf está la altitud del avión.
- Contestar
- f>0,\;f'<0,\;f''>0
51) Los precios de las acciones están en su punto máximo. Aquíf está el precio de las acciones.
52) La economía está cobrando velocidad. Aquíf hay una medida de la economía, como el PIB.
- Contestar
- f>0,\;f'>0,\;f''>0
Para los ejercicios 53 - 57, considere un polinomio de tercer gradof(x), que tenga las propiedadesf'(1)=0 yf'(3)=0.
Determinar si las siguientes afirmaciones son verdaderas o falsas. Justifica tu respuesta.
53)f(x)=0 para algunos1≤x≤3.
54)f''(x)=0 para algunos1≤x≤3.
- Contestar
- Cierto, por el Teorema del Valor Medio
55) No hay un máximo absoluto enx=3.
56) Sif(x) tiene tres raíces, entonces tiene punto de1 inflexión.
- Contestar
- Cierto, examinar derivado
57) Sif(x) tiene un punto de inflexión, entonces tiene tres raíces reales.

