4.5: Derivadas y la Forma de una Gráfica
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Explicar cómo el signo de la primera derivada afecta la forma de la gráfica de una función.
- Declarar la primera prueba derivada para puntos críticos.
- Utilice puntos de concavidad e inflexión para explicar cómo el signo de la segunda derivada afecta la forma de la gráfica de una función.
- Explicar la prueba de concavidad para una función en un intervalo abierto.
- Explicar la relación entre una función y sus derivadas primera y segunda.
- Anotar la segunda prueba derivada para los extremos locales.
Anteriormente en este capítulo afirmamos que si una funciónf tiene un extremo local en un puntoc, entoncesc debe ser un punto crítico def. Sin embargo, no se garantiza que una función tenga un extremo local en un punto crítico. Por ejemplo,f(x)=x3 tiene un punto crítico enx=0 ya quef′(x)=3x2 es cero enx=0, perof no tiene un extremo local enx=0. Utilizando los resultados de la sección anterior, ahora podemos determinar si un punto crítico de una función corresponde realmente a un valor extremo local. En esta sección, también vemos cómo la segunda derivada proporciona información sobre la forma de una gráfica al describir si la gráfica de una función se curva hacia arriba o se curva hacia abajo.
La Primera Prueba Derivada
El corolario3 del Teorema del Valor Medio mostró que si la derivada de una función es positiva en un intervaloI entonces la función está aumentandoI. Por otro lado, si la derivada de la función es negativa a lo largo de un intervaloI, entonces la función está disminuyendoI como se muestra en la siguiente figura.
Una función continuaf tiene un máximo local en el puntoc si y solo sif cambia de aumentar a disminuir en el puntoc. De igual manera,f tiene un mínimo local enc si y solo sif cambia de disminuir a aumentar enc. Sif es una función continua sobre un intervaloI que contienec y diferenciable sobreI, excepto posiblemente enc, la única maneraf puede pasar de aumentar a disminuir (o viceversa) en el puntoc es sif′ cambia signo como xaumenta a través dec. Sif es diferenciable enc, la única manera quef′ puede cambiar de signo a medida quex aumenta a travésc es sif′(c)=0. Por lo tanto, para una funciónf que es continua a lo largo de un intervaloI que contienec y diferenciable sobreIc, excepto posiblemente en, la única maneraf de pasar de aumentar a disminuir (o viceversa) es sif′(c)=0 of′(c) es indefinida. En consecuencia, para ubicar los extremos locales para una funciónf, buscamos puntosc en el dominio def tal quef′(c)=0 of′(c) sea indefinido. Recordemos que tales puntos se denominan puntos críticos def.
Tenga en cuenta que no esf necesario tener un extremo local en un punto crítico. Los puntos críticos son candidatos únicamente a los extremos locales. En la Figura4.5.2, mostramos que si una función continuaf tiene un extremo local, debe ocurrir en un punto crítico, pero una función puede no tener un extremo local en un punto crítico. Mostramos que sif tiene un extremo local en un punto crítico, entonces el signo def′ cambia comox aumenta a través de ese punto.
Utilizando la Figura4.5.2, se resumen los principales resultados con respecto a los extremos locales.
- Si una función continuaf tiene un extremo local, debe ocurrir en un punto críticoc.
- La función tiene un extremo local en el punto críticoc si y solo si losf′ interruptores derivados firman comox aumenta a travésc.
- Por lo tanto, para probar si una función tiene un extremo local en un punto críticoc, debemos determinar el signo def′(x) a la izquierda y derecha dec.
Este resultado se conoce como la primera prueba derivada.
Supongamos quef es una función continua sobre un intervaloI que contiene un punto críticoc. Sif es diferenciable sobreI, excepto posiblemente en el puntoc, entoncesf(c) satisface una de las siguientes descripciones:
- Sif′ cambia signo de positivo cuandox<c a negativo cuandox>c, entoncesf(c) es un máximo local def.
- Sif′ cambia signo de negativo cuandox<c a positivo cuandox>c, entoncesf(c) es un mínimo local def.
- Sif′ tiene el mismo signo parax<c yx>c, entonces nof(c) es ni un máximo local ni un mínimo local def
Ahora veamos cómo usar esta estrategia para localizar todos los extremos locales para funciones particulares.
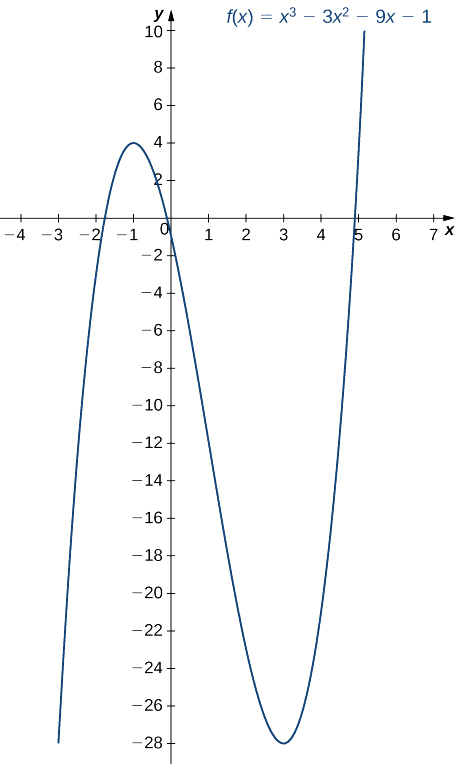
Utilice la primera prueba derivada para encontrar la ubicación de todos los extremos locales paraf(x)=x3−3x2−9x−1. Use una utilidad gráfica para confirmar sus resultados.
Solución
Paso 1. La derivada esf′(x)=3x2−6x−9. Para encontrar los puntos críticos, necesitamos encontrar dondef′(x)=0. Factorizar el polinomio, concluimos que los puntos críticos deben satisfacer
3(x2−2x−3)=3(x−3)(x+1)=0.
Por lo tanto, los puntos críticos sonx=3,−1. Ahora dividir el intervalo(−∞,∞) en los intervalos más pequeños(−∞,−1),(−1,3) y(3,∞).
Paso 2. Dado quef′ es una función continua, para determinar el signo def′(x) sobre cada subintervalo, basta con elegir un punto sobre cada uno de los intervalos(−∞,−1),(−1,3) y(3,∞) y determinar el signo def′ en cada uno de estos puntos. Por ejemplo, vamos a elegirx=−2,x=0, yx=4 como puntos de prueba.
| Intervalo | Punto de prueba | Signo def′(x)=3(x−3)(x+1) en el punto de prueba | Conclusión |
|---|---|---|---|
| (−∞,−1) | x=−2 | \ (f' (x) =3 (x−3) (x+1)\) en el punto de prueba” style="vertical-align:middle; "> (+) (−) (−) =+ | fva en aumento. |
| (−1,3) | x=0 | \ (f' (x) =3 (x−3) (x+1)\) en el punto de prueba” style="vertical-align:middle; "> (+) (−) (+) =- | fes decreciente. |
| (3,∞) | x=4 | \ (f' (x) =3 (x−3) (x+1)\) en el punto de prueba” style="vertical-align:middle; "> (+) (+) (+) =+ | fva en aumento. |
Paso 3. Dado quef′ cambia signo de positivo a negativo a medida quex aumenta a través de−1,f tiene un máximo local enx=−1. Dado quef′ cambia signo de negativo a positivo a medida quex aumenta a través de3,f tiene un mínimo local enx=3. Estos resultados analíticos concuerdan con la siguiente gráfica.
Utilice la primera prueba derivada para localizar todos los extremos locales paraf(x)=−x3+32x2+18x.
- Pista
-
Encuentre todos los puntos críticosf y determine los signos def′(x) en intervalos particulares determinados por los puntos críticos.
- Responder
-
ftiene un mínimo local en−2 y un máximo local en3.
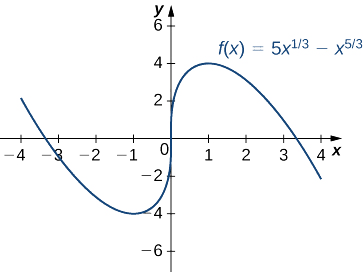
Utilice la primera prueba derivada para encontrar la ubicación de todos los extremos locales paraf(x)=5x1/3−x5/3. Use una utilidad gráfica para confirmar sus resultados.
Solución
Paso 1. El derivado es
f′(x)=53x−2/3−53x2/3=53x2/3−5x2/33=5−5x4/33x2/3=5(1−x4/3)3x2/3.
El derivadof′(x)=0 cuando1−x4/3=0. Por lo tanto,f′(x)=0 enx=±1. La derivadaf′(x) es indefinida enx=0. Por lo tanto, tenemos tres puntos críticos:x=0,x=1, yx=−1. En consecuencia, dividir el intervalo(−∞,∞) en los intervalos más pequeños(−∞,−1),(−1,0),(0,1), y(1,∞).
Paso 2: Dado quef′ es continuo sobre cada subintervalo, basta con elegir un punto de pruebax en cada uno de los intervalos del paso 1 y determinar el signo def′ en cada uno de estos puntos. Los puntosx=−2,x=−12,x=12, yx=2 son puntos de prueba para estos intervalos.
| Intervalo | Punto de prueba | Signo def′(x)=5(1−x4/3)3x2/3 en el punto de prueba | Conclusión |
|---|---|---|---|
| (−∞,−1) | x=−2 | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) en el Punto de Prueba” style="vertical-align:middle; ">(+)(−)+=− | fes decreciente. |
| (−1,0) | x=−12 | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) en el Punto de Prueba” style="vertical-align:middle; ">(+)(+)+=+ | fva en aumento. |
| (0,1) | x=12 | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) en el Punto de Prueba” style="vertical-align:middle; ">(+)(+)+=+ | fva en aumento. |
| (1,∞) | x=2 | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) en el Punto de Prueba” style="vertical-align:middle; ">(+)(−)+=− | fes decreciente. |
Paso 3: Dado quef está disminuyendo a lo largo del intervalo(−∞,−1) y aumentando a lo largo del intervalo(−1,0),f tiene un mínimo local enx=−1. Dado quef va aumentando a lo largo del intervalo(−1,0) y el intervalo(0,1),f no tiene un extremo local enx=0. Ya quef está aumentando a lo largo del intervalo(0,1) y disminuyendo a lo largo del intervalo(1,∞),f tiene un máximo local enx=1. Los resultados analíticos concuerdan con la siguiente gráfica.
Utilice la primera prueba derivada para encontrar todos los extremos locales paraf(x)=3x−1.
- Pista
-
El único punto crítico def esx=1.
- Responder
-
fno tiene extrema local porquef′ no cambia de señal enx=1.
Concavidad y Puntos de Inflexión
Ahora sabemos determinar dónde está aumentando o disminuyendo una función. Sin embargo, hay otro tema a considerar respecto a la forma de la gráfica de una función. Si la gráfica se curva, ¿se curva hacia arriba o se curva hacia abajo? Esta noción se llama la concavidad de la función.
La figura4.5.5a muestra una funciónf con una gráfica que se curva hacia arriba. Ax medida que aumenta, la pendiente de la línea tangente aumenta. Así, dado que la derivada aumenta a medida quex aumenta,f′ es una función creciente. Decimos que esta funciónf es cóncava hacia arriba. La figura4.5.5b muestra una funciónf que se curva hacia abajo. Ax medida que aumenta, la pendiente de la línea tangente disminuye. Dado que la derivada disminuye a medida quex aumenta,f′ es una función decreciente. Decimos que esta funciónf es cóncava hacia abajo.
Dejarf ser una función que sea diferenciable en un intervalo abiertoI. Sif′ está aumentandoI, decimos quef es cóncavo hacia arriba sobreI. Sif′ está disminuyendo por encimaI, decimos quef es cóncavo hacia abajo sobreI.
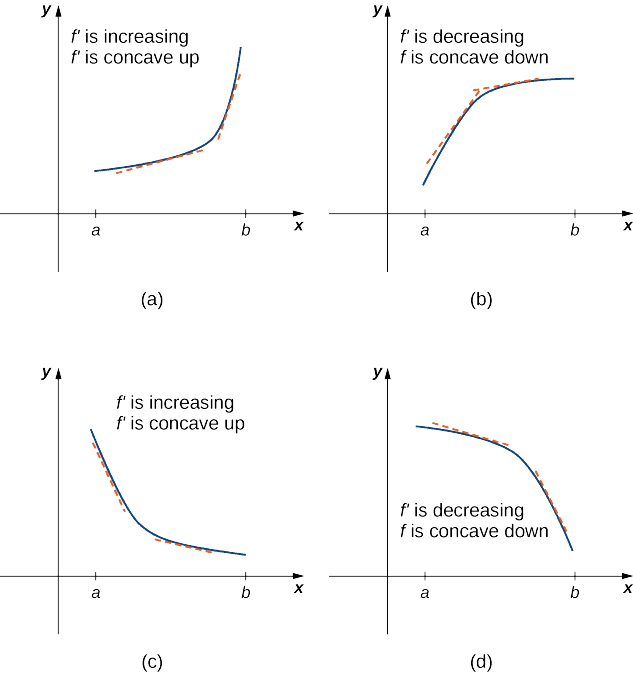
En general, sin tener la gráfica de una funciónf, ¿cómo podemos determinar su concavidad? Por definición, una funciónf es cóncava hacia arriba sif′ va en aumento. Desde Corolario3, sabemos que sif′ es una función diferenciable, entoncesf′ está aumentando si su derivadaf″(x)>0. Por lo tanto, una funciónf que es dos veces diferenciable es cóncava hacia arriba cuandof″(x)>0. Del mismo modo, una funciónf es cóncava hacia abajo sif′ es decreciente. Sabemos que una función diferenciablef′ es decreciente si su derivadaf″(x)<0. Por lo tanto, una función dos veces diferenciablef es cóncava hacia abajo cuandof″(x)<0. La aplicación de esta lógica se conoce como prueba de concavidad.
Dejarf ser una función que es dos veces diferenciable a lo largo de un intervaloI.
- Sif″(x)>0 por todosx∈I, entoncesf es cóncavo hacia arribaI
- Sif″(x)<0 para todosx∈I, entoncesf es cóncavo hacia abajo sobreI.
Concluimos que podemos determinar la concavidad de una funciónf observando la segunda derivada def. Además, observamos que una funciónf puede conmutar concavidad (Figura4.5.6). Sin embargo, una función continua puede cambiar la concavidad solo en un puntox sif″(x)=0 of″(x) es indefinido. En consecuencia, para determinar los intervalos donde una funciónf es cóncava hacia arriba y cóncava hacia abajo, buscamos aquellos valores dex dondef″(x)=0 of″(x) es indefinido. Cuando hemos determinado estos puntos, dividimos el dominio def en intervalos más pequeños y determinamos el signo def″ sobre cada uno de estos intervalos más pequeños. Sif″ los cambios firman a medida que pasamos por un puntox, entoncesf cambia la concavidad. Es importante recordar que una funciónf puede no cambiar la concavidad en un puntox incluso sif″(x)=0 of″(x) es indefinida. Si, sin embargo,f sí cambia la concavidad en un puntoa yf es continuo ena, decimos que el punto(a,f(a)) es un punto de inflexión def.
Sif es continuo ena yf cambia la concavidad ena, el punto(a,f(a)) es un punto de inflexión def.
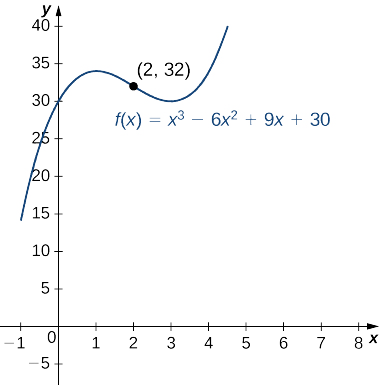
Para la funciónf(x)=x3−6x2+9x+30, determinar todos los intervalos dondef es cóncavo hacia arriba y todos los intervalos dondef es cóncavo hacia abajo. Enumere todos los puntos de inflexión paraf. Utilice una utilidad gráfica para confirmar sus resultados.
Solución
Para determinar la concavidad, necesitamos encontrar la segunda derivadaf″(x). La primera derivada esf′(x)=3x2−12x+9, así que la segunda derivada esf″(x)=6x−12. Si la función cambia la concavidad, ocurre ya sea cuandof″(x)=0 of″(x) es indefinida. Ya quef″ se define para todos los números realesx, solo necesitamos encontrar dóndef″(x)=0. Resolviendo la ecuación6x−12=0, vemos quex=2 es el único lugar dondef podría cambiar la concavidad. Ahora probamos puntos a lo largo de los intervalos(−∞,2) y(2,∞) para determinar la concavidad def. Los puntosx=0 yx=3 son puntos de prueba para estos intervalos.
| Intervalo | Punto de prueba | Signo def″(x)=6x−12 en el punto de prueba | Conclusión |
|---|---|---|---|
| (−∞,2) | x=0 | \ (f "(x) =6x−12\) en el punto de prueba” style="vertical-align:middle; ">− | fes cóncavo hacia abajo |
| (2,∞) | x=3 | \ (f "(x) =6x−12\) en el punto de prueba” style="vertical-align:middle; ">+ | fes cóncavo hacia arriba |
Concluimos quef es cóncavo hacia abajo en el intervalo(−∞,2) y cóncavo hacia arriba en el intervalo(2,∞). Dado quef cambia la concavidad enx=2, el punto(2,f(2))=(2,32) es un punto de inflexión. La figura4.5.7 confirma los resultados analíticos.
Paraf(x)=−x3+32x2+18x, encontrar todos los intervalos dondef es cóncavo hacia arriba y todos los intervalos dondef es cóncavo abajo.
- Pista
-
Encuentra dóndef″(x)=0
- Responder
-
fes cóncavo hacia arriba en el intervalo(−∞,12) y cóncavo hacia abajo en el intervalo(12,∞)
Ahora resumimos, en Tabla4.5.4, la información que la primera y segunda derivadas de una funciónf proporcionan sobre la gráfica def, e ilustramos esta información en la Figura4.5.8.
| Signo def′ | Signo def″ | ¿Estáf aumentando o disminuyendo? | Concavidad |
|---|---|---|---|
| \ (f'\)” style="vertical-align:middle; ">Positivo | \ (f "\)” style="vertical-align:middle; ">Positivo | \ (f\) ¿aumentando o disminuyendo?” style="vertical-align:middle; ">Incrementando | Cóncavo arriba |
| \ (f'\)” style="vertical-align:middle; ">Positivo | \ (f "\)” style="vertical-align:middle; ">Negativo | \ (f\) ¿aumentando o disminuyendo?” style="vertical-align:middle; ">Incrementando | Abajo cóncavo |
| \ (f'\)” style="vertical-align:middle; ">Negativo | \ (f "\)” style="vertical-align:middle; ">Positivo | \ (f\) ¿aumentando o disminuyendo?” style="vertical-align:middle; ">Disminución | Cóncavo arriba |
| \ (f'\)” style="vertical-align:middle; ">Negativo | \ (f "\)” style="vertical-align:middle; ">Negativo | \ (f\) ¿aumentando o disminuyendo?” style="vertical-align:middle; ">Disminución | Abajo cóncavo |
La Segunda Prueba Derivada
La prueba de la primera derivada proporciona una herramienta analítica para encontrar extremos locales, pero la segunda derivada también se puede utilizar para localizar valores extremos. El uso de la segunda derivada a veces puede ser un método más sencillo que usar la primera derivada.
Sabemos que si una función continua tiene un extremo local, debe ocurrir en un punto crítico. Sin embargo, una función no necesita tener un extremo local en un punto crítico. Aquí examinamos cómo se puede utilizar la prueba de la segunda derivada para determinar si una función tiene un extremo local en un punto crítico. Dejarf ser una función dos veces diferenciable tal quef′(a)=0 yf″ es continua a lo largo de un intervalo abiertoI que contienea. Supongamosf″(a)<0. Ya quef″ es continuoI,f″(x)<0 para todosx∈I (Figura4.5.9). Entonces, por Corolario3,f′ es una función decreciente sobreI. Ya quef′(a)=0, concluimos que para todosx∈I,f′(x)>0 six<a yf′(x)<0 six>a. Por lo tanto, por la primera prueba derivada,f tiene un máximo local ax=a.
Por otro lado, supongamos que existe un puntob tal quef′(b)=0 perof″(b)>0. Dado quef″ es continuo sobre un intervalo abiertoI que contieneb, entoncesf″(x)>0 para todosx∈I (Figura4.5.9). Entonces, por Corolario3,f′ es una función creciente sobreI. Ya quef′(b)=0, concluimos que para todosx∈I,f′(x)<0 six<b yf′(x)>0 six>b. Por lo tanto, por la primera prueba derivada,f tiene un mínimo local enx=b.
Supongamosf′(c)=0 yf″ es continuo sobre un intervalo que contienec.
- Sif″(c)>0, entoncesf tiene un mínimo local enc.
- Sif″(c)<0, entoncesf tiene un máximo local enc.
- Sif″(c)=0, entonces la prueba no es concluyente.
Tenga en cuenta que para el caso iii. cuandof″(c)=0, entoncesf puede tener un máximo local, mínimo local, o ninguno alc. Por ejemplo, las funcionesf(x)=x3,f(x)=x4, yf(x)=−x4 todas tienen puntos críticos enx=0. En cada caso, la segunda derivada es cero atx=0. Sin embargo, la funciónf(x)=x4 tiene un mínimo local enx=0 mientras que la funciónf(x)=−x4 tiene un máximo local atx=0, y la funciónf(x)=x3 no tiene un extremo local atx=0.
Veamos ahora cómo usar la segunda prueba derivada para determinar sif tiene un máximo local o un mínimo local en un punto críticoc dondef′(c)=0.
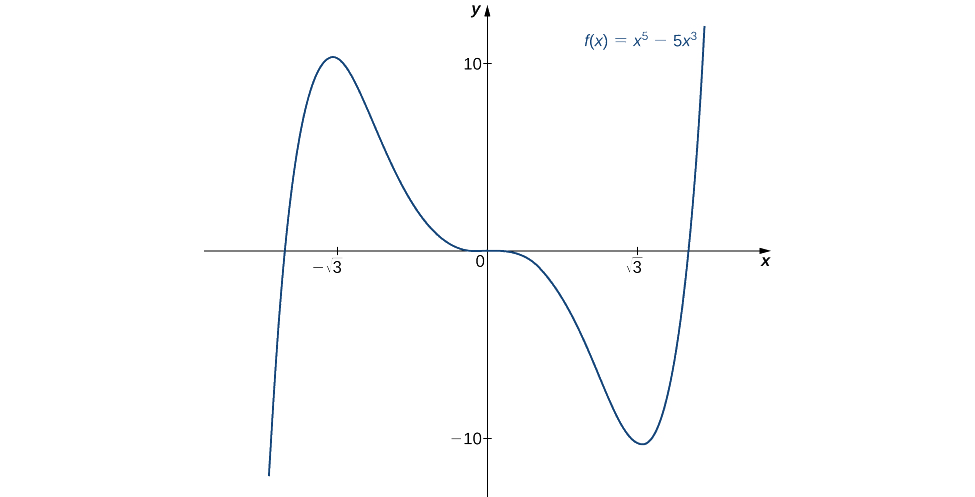
Utilice la segunda derivada para encontrar la ubicación de todos los extremos locales paraf(x)=x5−5x3.
Solución
Para aplicar la segunda prueba derivada, primero necesitamos encontrar puntos críticosc dondef′(c)=0. El derivado esf′(x)=5x4−15x2. Por lo tanto,f′(x)=5x4−15x2=5x2(x2−3)=0 cuandox=0,±√3.
Para determinar sif tiene un extremo local en alguno de estos puntos, necesitamos evaluar el signo def″ en estos puntos. La segunda derivada es
f″(x)=20x3−30x=10x(2x2−3).
En la siguiente tabla, evaluamos la segunda derivada en cada uno de los puntos críticos y utilizamos la prueba de la segunda derivada para determinar sif tiene un máximo local o un mínimo local en alguno de estos puntos.
| x | f″(x) | Conclusión |
|---|---|---|
| \ (x\) ">−√3 | \ (f "(x)\)" >−30√3 | Máximo local |
| \ (x\) ">0 | \ (f "(x)\)" >0 | La prueba de la segunda derivada no es concluyente |
| \ (x\) ">√3 | \ (f "(x)\)" >30√3 | Mínimo local |
Por la segunda prueba derivada, concluimos quef tiene un máximo local enx=−√3 yf tiene un mínimo local enx=√3. La segunda prueba derivada no es concluyente enx=0. Para determinar sif tiene un extremo local enx=0, aplicamos la primera prueba derivada. Evaluar el signo def′(x)=5x2(x2−3) parax∈(−√3,0) yx∈(0,√3), dejarx=−1 yx=1 ser los dos puntos de prueba. Desdef′(−1)<0 yf′(1)<0, concluimos quef está disminuyendo en ambos intervalos y, por lo tanto,f no tiene un extremo local enx=0 como se muestra en la siguiente gráfica.
Considera la funciónf(x)=x3−(32)x2−18x. Los puntosc=3,−2 satisfacenf′(c)=0. Utilice la prueba de la segunda derivada para determinar sif tiene un máximo local o un mínimo local en esos puntos.
- Pista
-
f″(x)=6x−3
- Responder
-
ftiene un máximo local en−2 y un mínimo local en3.
Ahora hemos desarrollado las herramientas que necesitamos para determinar dónde está aumentando y disminuyendo una función, además de adquirir una comprensión de la forma básica de la gráfica. En la siguiente sección discutimos lo que sucede con una función comox→±∞. En ese punto, contamos con herramientas suficientes para proporcionar gráficas precisas de una gran variedad de funciones.
Conceptos clave
- Sic es un punto crítico def yf′(x)>0 parax<c yf′(x)<0 parax>c, entoncesf tiene un máximo local enc.
- Sic es un punto crítico def yf′(x)<0 parax<c yf′(x)>0 parax>c, entoncesf tiene un mínimo local enc.
- Si estáf″(x)>0 sobre un intervaloI, entoncesf es cóncavo hacia arribaI.
- Si estáf″(x)<0 sobre un intervaloI, entoncesf es cóncavo hacia abajo sobreI.
- Sif′(c)=0 yf″(c)>0, entoncesf tiene un mínimo local enc.
- Sif′(c)=0 yf″(c)<0, entoncesf tiene un máximo local enc.
- Sif′(c)=0 yf″(c)=0, luego evaluarf′(x) en un punto de pruebax a la izquierdac y un punto de pruebax a la derecha dec, para determinar sif tiene un extremo local enc.
Glosario
- cóncavo hacia abajo
- sif es diferenciable a lo largo de un intervaloI yf′ está disminuyendo sobreI, entoncesf es cóncavo hacia abajo sobreI
- cóncavo hacia arriba
- sif es diferenciable a lo largo de un intervaloI yf′ está aumentandoI, entoncesf es cóncavo hacia arriba sobreI
- concavidad
- la curva ascendente o descendente de la gráfica de una función
- prueba de concavidad
- supongamos quef es dos veces diferenciable en un intervaloI; si estáf″>0 terminadoI, entoncesf es cóncavo hacia arribaI; si estáf″< terminadoI, entoncesf es cóncavo hacia abajo sobreI
- prueba de primera derivada
- dejarf ser una función continua sobre un intervaloI que contiene un punto críticoc tal quef es diferenciableI excepto posiblemente enc; sif′ cambia signo de positivo a negativo a medida quex aumenta a travésc, entonces ftiene un máximo local enc; sif′ los cambios firman de negativo a positivo a medida quex aumenta a travésc, entoncesf tiene un mínimo local enc; sif′ no cambia signo a medida quex aumenta a travésc, entoncesf no tiene un extremo local enc
- punto de inflexión
- sif es continuo enc yf cambia la concavidad enc, el punto(c,f(c)) es un punto de inflexión def
- prueba de segunda derivada
- supongaf′(c)=0 yf′ 'es continuo sobre un intervalo que contienec; sif″(c)>0, entoncesf tiene un mínimo local enc; sif″(c)<0, entoncesf tiene un máximo local enc; sif″(c)=0, entonces la prueba no es concluyente


