8.3: Ecuaciones separables

Objetivos de aprendizaje

• Utilizar la separación de variables para resolver una ecuación diferencial.
• Resolver aplicaciones usando separación de variables.

Ahora examinamos una técnica de solución para encontrar soluciones exactas a una clase de ecuaciones diferenciales conocidas como ecuaciones diferenciales separables. Estas ecuaciones son comunes en una amplia variedad de disciplinas, incluyendo física, química e ingeniería. Ilustramos algunas aplicaciones al final de la sección.

Separación de Variables

Comenzamos con una definición y algunos ejemplos.

Definición: Ecuaciones diferenciales separables

Una ecuación diferencial separable es cualquier ecuación que se puede escribir en la forma

\[y'=f(x)g(y). \label{sep} \]

El término 'separable' se refiere al hecho de que el lado derecho de la Ecuación\ ref {sep} se puede separar en una función de\(x\) veces una función de\(y\). Los ejemplos de ecuaciones diferenciales separables incluyen

\[ \begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align} \]

La ecuación\ ref {eq2} es separable con\(f(x)=6x^2+4x\) y\(g(y)=1\), La ecuación\ ref {eq3} es separable con\(f(x)=1\)\(g(y)=\sec y+\tan y,\) y y el lado derecho de la ecuación\ ref {eq4} se puede factorizar como\((x+3)(y−2)\), por lo que también es separable. La ecuación\ ref {eq3} también se llama ecuación diferencial autónoma porque el lado derecho de la ecuación es una función de\(y\) solo. Si una ecuación diferencial es separable, entonces es posible resolver la ecuación utilizando el método de separación de variables.

Estrategia de Resolución de Problemas: Separación de Variables

1. Comprueben los valores de\(y\) que hacen que\(g(y)=0.\) estos correspondan a soluciones constantes.
2. Reescribir la ecuación diferencial en la forma\[ \dfrac{dy}{g(y)}=f(x)dx. \nonumber \]
3. Integrar ambos lados de la ecuación.
4. Resolver la ecuación resultante para\(y\) si es posible.
5. Si existe una condición inicial, sustituya los valores apropiados para\(x\) y\(y\) en la ecuación y resuelva por la constante.

Tenga en cuenta que el Paso 4 establece “Resuelve la ecuación resultante para\(y\) si es posible”. No siempre es posible obtener\(y\) como una función explícita de\(x\). Muy a menudo tenemos que estar satisfechos con encontrar y como una función implícita de\(x\).

Ejemplo\(\PageIndex{1}\): Using Separation of Variables

Encontrar una solución general a la ecuación diferencial\(y'=(x^2−4)(3y+2)\) utilizando el método de separación de variables.

Solución

Siga el método de separación de variables en cinco pasos.

1. En este ejemplo,\(f(x)=x^2−4\) y\(g(y)=3y+2\). \(g(y)=0\)El fraguado da\(y=−\dfrac{2}{3}\) como una solución constante.

2. Reescribir la ecuación diferencial en la forma

\[ \dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber \]

3. Integrar ambos lados de la ecuación:

\[ ∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber \]

Vamos\(u=3y+2\). Entonces\(du=3\dfrac{dy}{dx}\,dx\), así la ecuación se convierte

\[ \dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber \]

4. Para resolver esta ecuación para\(y\), primero multiplique ambos lados de la ecuación por\(3\).

\[ \ln|3y+2|=x^3−12x+3C\nonumber \]

Ahora usamos alguna lógica para tratar con la constante\(C\). Dado que\(C\) representa una constante arbitraria,\(3C\) también representa una constante arbitraria. Si llamamos a la segunda constante arbitraria\(C_1,\) donde\(C_1 = 3C,\) la ecuación se convierte

\[ \ln|3y+2|=x^3−12x+C_1.\nonumber \]

Ahora exponenciar ambos lados de la ecuación (es decir, hacer que cada lado de la ecuación sea el exponente para la base\(e\)).

\[ \begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}\]

Nuevamente definir una nueva constante\(C_2= e^{C_1}\) (tenga en cuenta que\(C_2 > 0\)):

\[ |3y+2|=C_2e^{x^3−12x}.\nonumber \]

Debido al valor absoluto en el lado izquierdo de la ecuación, esto corresponde a dos ecuaciones separadas:

\[3y+2=C_2e^{x^3−12x}\nonumber \]

y

\[3y+2=−C_2e^{x^3−12x}.\nonumber \]

La solución a cualquiera de las dos ecuaciones se puede escribir en la forma

\[y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber \]

Ya que\(C_2>0\), no importa si usamos más o menos, por lo que la constante en realidad puede tener cualquiera de los dos signos. Además, el subíndice en la constante\(C\) es completamente arbitrario y puede ser descartado. Por lo tanto, la solución puede escribirse como

\[ y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber \]

Obsérvese que por escrito una única solución general de esta manera, también estamos permitiendo\(C\) igualar\(0\). Esto nos da la solución singular,\(y = -\dfrac{2}{3}\), para la ecuación diferencial dada. ¡Comprueba que esta es efectivamente una solución de esta ecuación diferencial!

5. No se impone ninguna condición inicial, así que estamos terminados.

Ejercicio\(\PageIndex{1}\)

Utilizar el método de separación de variables para encontrar una solución general a la ecuación diferencial

\[ y'=2xy+3y−4x−6. \nonumber \]

Pista

Primero factorizar el lado derecho de la ecuación agrupando, luego use la estrategia de cinco pasos de separación de variables.

Contestar

\[ y=2+Ce^{x^2+3x} \nonumber \]

Ejemplo\(\PageIndex{2}\): Solving an Initial-Value Problem

Usando el método de separación de variables, resolver el problema del valor inicial

\[ y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber \]

Solución

Siga el método de separación de variables en cinco pasos.

1. En este ejemplo,\(f(x)=2x+3\) y\(g(y)=y^2−4\). \(g(y)=0\)El fraguado da\(y=±2\) como soluciones constantes.

2. Dividir ambos lados de la ecuación por\(y^2−4\) y multiplicar por\(dx\). Esto da la ecuación

\[\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber \]

3. A continuación, integre ambos lados:

\[∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2} \]

Para evaluar el lado izquierdo, utilice el método de descomposición parcial de la fracción. Esto lleva a la identidad

\[\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber \]

Entonces la Ecuación\ ref {Ex2.2} se convierte

\[\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber \]

\[\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber \]

Multiplicar ambos lados de esta ecuación por\(4\) y reemplazar\(4C\) con\(C_1\) da

\[\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber \]

\[\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber \]

4. Es posible resolver esta ecuación para\(y.\) Primero exponenciar ambos lados de la ecuación y definir\(C_2=e^{C_1}\):

\[\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber \]

A continuación podemos eliminar el valor absoluto y dejar que una nueva constante\(C_3\) sea positiva, negativa o cero, es decir,\(C_3 =\pm C_2\) o\(C_3 = 0.\)

Después multiplicar ambos lados por\(y+2\).

\[y−2=C_3(y+2)e^{4x^2+12x}\nonumber \]

\[y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber \]

Ahora recoja todos los términos que involucren\(y\) en un lado de la ecuación y resuelva para\(y\):

\[y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber \]

\[y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber \]

\[y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber \]

5. Determinar el valor de\(C_3\), sustituir\(x=0\) y\(y=−1\) en la solución general. Alternativamente, podemos poner los mismos valores en una ecuación anterior, a saber, la ecuación\(\dfrac{y−2}{y+2}=C_3e^{4x^2+12}\). Esto es mucho más fácil de resolver para\(C_3\):

\[\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber \]

\[\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber \]

\[C_3=−3.\nonumber \]

Por lo tanto, la solución al problema del valor inicial es

\[y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber \]

Una gráfica de esta solución aparece en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Gráfica de la solución al problema del valor inicial\(y'=(2x+3)(y^2−4),y(0)=−1\).

Ejercicio\(\PageIndex{2}\)

Encuentre la solución al problema del valor inicial

\[ 6y'=(2x+1)(y^2−2y−8) \nonumber \]

con el\(y(0)=−3\) uso del método de separación de variables.

Pista

Siga los pasos para la separación de variables para resolver el problema del valor inicial.

Contestar

\[ y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber \]

Aplicaciones de Separación de Variables

Muchos problemas interesantes pueden ser descritos por ecuaciones separables. Ilustramos dos tipos de problemas: las concentraciones de soluciones y la ley de enfriamiento de Newton.

Concentraciones de solución

Considera llenar un tanque con una solución salina. Nos gustaría determinar la cantidad de sal presente en el tanque en función del tiempo. Podemos aplicar el proceso de separación de variables para resolver este problema y problemas similares que involucran concentraciones de solución.

Ejemplo\(\PageIndex{3}\): Determining Salt Concentration over Time

Un tanque que contiene\(100\) L de una solución de salmuera inicialmente tiene\(4\) kg de sal disuelta en la solución. En el momento\(t=0\), otra solución de salmuera fluye hacia el tanque a una velocidad de\(2\) L/min. Esta solución de salmuera contiene una concentración de\(0.5\) Kg/L de sal. Al mismo tiempo, se abre una válvula de paso en el fondo del tanque, permitiendo que la solución combinada fluya hacia fuera a una velocidad de\(2\) L/min, de manera que el nivel de líquido en el tanque permanezca constante (Figura\(\PageIndex{2}\)). Encuentra la cantidad de sal en el tanque en función del tiempo (medida en minutos), y encuentra la cantidad limitante de sal en el tanque, asumiendo que la solución en el tanque está bien mezclada en todo momento.

Figura\(\PageIndex{2}\): Un tanque de salmuera con una cantidad inicial de solución salina acepta un flujo de entrada y entrega un flujo de salida. ¿Cómo cambia la cantidad de sal con el tiempo?

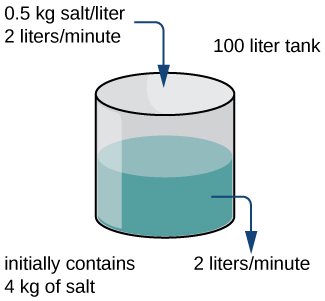
Solución

Primero definimos una función\(u(t)\) que representa la cantidad de sal en kilogramos en el tanque en función del tiempo. Entonces\(\dfrac{du}{dt}\) representa la velocidad a la que la cantidad de sal en el tanque cambia en función del tiempo. También,\(u(0)\) representa la cantidad de sal en el tanque en el momento\(t=0\), que es\(4\) kilogramos.

La configuración general para la ecuación diferencial que resolveremos es de la forma

\[\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber \]

TASA DE ENTRADA representa la velocidad a la que la sal ingresa al tanque, y la tasa de flujo de salida representa la velocidad a la que la sal sale del tanque. Debido a que la solución ingresa al tanque a una velocidad de\(2\) L/min, y cada litro de solución contiene\(0.5\) kilogramo de sal, cada minuto\(2(0.5)=1\) kilogramo de sal ingresa al tanque. Por lo tanto TASA DE ENTRADA =\(1\).

Para calcular la velocidad a la que la sal sale del tanque, necesitamos la concentración de sal en el tanque en cualquier momento. Dado que la cantidad real de sal varía con el tiempo, también lo hace la concentración de sal. Sin embargo, el volumen de la solución permanece fijo en 100 litros. El número de kilogramos de sal en el tanque en el momento\(t\) es igual a\(u(t)\). Así, la concentración de sal es\(\dfrac{u(t)}{100}\) Kg/L, y la solución sale del tanque a una velocidad de\(2\) L/min. Por lo tanto, la sal sale del tanque a una velocidad de\(\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}\) kg/min, y la TASA DE SALIDA es igual a\(\dfrac{u(t)}{50}\). Por lo tanto la ecuación diferencial se convierte\(\dfrac{du}{dt}=1−\dfrac{u}{50}\), y la condición inicial es\(u(0)=4.\) El problema del valor inicial a resolver es

\[\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber \]

La ecuación diferencial es una ecuación separable, por lo que podemos aplicar la estrategia de cinco pasos para la solución.

Paso 1. \(1−\dfrac{u}{50}=0\)El fraguado da\(u=50\) como una solución constante. Dado que la cantidad inicial de sal en el tanque es de\(4\) kilogramos, esta solución no aplica.

Paso 2. Reescribir la ecuación como

\[\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber \]

Luego multiplica ambos lados por\(dt\) y divide ambos lados por\(50−u:\)

\[\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber \]

Paso 3. Integrar ambos lados:

\[\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}\]

Paso 4. Resolver para\(u(t)\):

\[\ln|50−u|=−\dfrac{t}{50}−C\nonumber \]

\[e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber \]

\[|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber \]

Elimine el valor absoluto permitiendo que la constante sea positiva, negativa o cero, es decir,\(C_1 = \pm e^{-C}\) o\(C_1 = 0\):

\[50−u=C_1e^{−t/50}.\nonumber \]

Por último, resolver para\(u(t)\):

\[u(t)=50−C_1e^{−t/50}.\nonumber \]

Paso 5. Resolver para\(C_1\):

\[\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}\]

La solución al problema del valor inicial es\(u(t)=50−46e^{−t/50}.\) Para encontrar la cantidad limitante de sal en el tanque, tomar el límite a medida que se\(t\) acerca al infinito:

\[\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}\]

Obsérvese que esta fue la solución constante a la ecuación diferencial. Si la cantidad inicial de sal en el tanque es de\(50\) kilogramos, entonces permanece constante. Si comienza en menos de\(50\) kilogramos, entonces se acerca a\(50\) kilogramos con el tiempo.

Ejercicio\(\PageIndex{3}\)

Un tanque contiene\(3\) kilogramos de sal disueltos en\(75\) litros de agua. Una solución salina de\(0.4\) kg sal/L se bombea al tanque a una velocidad de\(6\) L/min y se drena a la misma velocidad. Resolver la concentración de sal en el momento\(t\). Supongamos que el tanque está bien mezclado en todo momento.

Pista

Siga los pasos de Ejemplo\(\PageIndex{3}\) y determine una expresión para INFLOW y SOFLOW. Formular un problema de valor inicial, y luego resolverlo.

Problema de valor inicial:

\[ \dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber \]

Contestar

\[u(t)=30−27e^{−t/50} \nonumber \]

Ley de Refrigeración de Newton

La ley de enfriamiento de Newton establece que la velocidad de cambio de la temperatura de un objeto es proporcional a la diferencia entre su propia temperatura y la temperatura ambiente (es decir, la temperatura de su entorno). Si dejamos\(T(t)\) representar la temperatura de un objeto en función del tiempo, entonces\(\dfrac{dT}{dt}\) representa la velocidad a la que cambia esa temperatura. La temperatura del entorno del objeto puede ser representada por\(T_s\). Entonces la ley de enfriamiento de Newton se puede escribir en la forma

\[ \dfrac{dT}{dt}=k(T(t)−T_s) \nonumber \]

o simplemente

\[ \dfrac{dT}{dt}=k(T−T_s). \nonumber \]

La temperatura del objeto al inicio de cualquier experimento es el valor inicial para el problema del valor inicial. A esto le llamamos temperatura\(T_0\). Por lo tanto, el problema del valor inicial que hay que resolver toma la forma

\[ \dfrac{dT}{dt}=k(T−T_s) \label{newton} \]

con\(T(0)=T_0\), donde\(k\) es una constante que necesita ser dada o determinada en el contexto del problema. Utilizamos estas ecuaciones en Ejemplo\(\PageIndex{4}\).

Ejemplo\(\PageIndex{4}\): Waiting for a Pizza to Cool

Una pizza se retira del horno después de hornear a fondo, y la temperatura del horno es\(350°F.\) La temperatura de la cocina es\(75°F\), y después de\(5\) minutos la temperatura de la pizza es\(340°F\). Nos gustaría esperar hasta que llegue la temperatura de la pizza\(300°F\) antes de cortarla y servirla (Figura\(\PageIndex{3}\)). ¿Cuánto tiempo más tendremos que esperar?

Figura\(\PageIndex{3}\): De la ley de enfriamiento de Newton, si la pizza se enfría\(10°F\) en\(5\) minutos, ¿cuánto tiempo antes de que se enfríe\(300°F\)?

Solución

La temperatura ambiente (temperatura circundante) es\(75°F\), entonces\(T_s=75\). La temperatura de la pizza cuando sale del horno es\(350°F\), que es la temperatura inicial (es decir, valor inicial), entonces\(T_0=350\). Por lo tanto, la ecuación\ ref {newton} se convierte

\[\dfrac{dT}{dt}=k(T−75) \nonumber \]

con\(T(0)=350.\)

Para resolver la ecuación diferencial, utilizamos la técnica de cinco pasos para resolver ecuaciones separables.

1. Establecer el lado derecho igual a cero da\(T=75\) como una solución constante. Dado que la pizza empieza en\(350°F,\) esta no es la solución que estamos buscando.

2. Reescriba la ecuación diferencial multiplicando ambos lados por\(dt\) y dividiendo ambos lados por\(T−75\):

\[\dfrac{dT}{T−75}=k\,dt. \nonumber \]

3. Integrar ambos lados:

\[\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber \]

4. Resuelve primero exponenciando ambos lados:\(T\)

\[\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber \]

5. Resolver para\(C\) mediante el uso de la condición inicial\(T(0)=350:\)

\[\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber \]

Por lo tanto, la solución al problema del valor inicial es

\[T(t)=75+275e^{kt}.\nonumber \]

Para determinar el valor de\(k\), necesitamos usar el hecho de que después de\(5\) minutos la temperatura de la pizza es\(340°F\). Por lo tanto,\(T(5)=340.\) sustituyendo esta información en la solución al problema del valor inicial, tenemos

\[T(t)=75+275e^{kt}\nonumber \]

\[T(5)=340=75+275e^{5k}\nonumber \]

\[265=275e^{5k}\nonumber \]

\[e^{5k}=\dfrac{53}{55}\nonumber \]

\[\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber \]

\[5k=\ln(\dfrac{53}{55})\nonumber \]

\[k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber \]

Entonces ahora tenemos ¿\(T(t)=75+275e^{−0.007048t}.\)Cuándo es la temperatura\(300°F\)? Resolviendo para\(t,\) nosotros encontramos

\[T(t)=75+275e^{−0.007048t}\nonumber \]

\[300=75+275e^{−0.007048t}\nonumber \]

\[225=275e^{−0.007048t}\nonumber \]

\[e^{−0.007048t}=\dfrac{9}{11}\nonumber \]

\[\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber \]

\[−0.007048t=\ln\dfrac{9}{11}\nonumber \]

\[t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber \]

Por lo tanto, tenemos que esperar\(23.5\) unos minutos adicionales (después de que la temperatura de la pizza haya alcanzado\(340°F\)). Ese debería ser el tiempo justo suficiente para terminar este cálculo.

Ejercicio\(\PageIndex{4}\)

Una torta se retira del horno después de hornear a fondo, y la temperatura del horno es\(450°F\). La temperatura de la cocina es\(70°F\), y después de\(10\) minutos la temperatura del pastel es\(430°F\).

1. Escriba el problema de valor inicial apropiado para describir esta situación.
2. Resolver el problema del valor inicial para\(T(t)\).
3. ¿Cuánto tiempo tardará hasta que la temperatura de la torta esté dentro\(5°F\) de la temperatura ambiente?

Pista

Determine los valores de\(T_s\) y\(T_0\) luego use la ecuación\ ref {newton}.

Contestar a

Problema de valor inicial\[\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber \]

Respuesta b

\[T(t)=70+380e^{kt}\nonumber \]

Respuesta c

\(114\)Minutos aproximadamente.

Conceptos clave

• Una ecuación diferencial separable es cualquier ecuación que se puede escribir en la forma\(y'=f(x)g(y).\)
• El método de separación de variables se utiliza para encontrar la solución general a una ecuación diferencial separable.

Ecuaciones Clave

• Ecuación diferencial separable

\(y′=f(x)g(y)\)

• Concentración de solución

\(\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}\)

• La ley del enfriamiento de Newton

\(\dfrac{dT}{dt}=k(T−T_s)\)

Glosario

ecuación diferencial autónoma

una ecuación en la que el lado derecho es una función de\(y\) solo

ecuación diferencial separable

cualquier ecuación que se pueda escribir en la forma\(y'=f(x)g(y)\)

separación de variables

un método utilizado para resolver una ecuación diferencial separable