9.2: Serie Infinita

Objetivos de aprendizaje

• Explicar el significado de la suma de una serie infinita.
• Calcular la suma de una serie geométrica.
• Evaluar una serie telescópica.

Hemos visto que una secuencia es un conjunto ordenado de términos. Si sumas estos términos juntos, obtienes una serie. En esta sección definimos una serie infinita y mostramos cómo las series se relacionan con las secuencias. También definimos lo que significa que una serie converja o diverja. Presentamos uno de los tipos de series más importantes: la serie geométrica. Utilizaremos series geométricas en el siguiente capítulo para escribir ciertas funciones como polinomios con un número infinito de términos. Este proceso es importante porque nos permite evaluar, diferenciar e integrar funciones complicadas mediante el uso de polinomios que son más fáciles de manejar. También discutimos la serie armónica, posiblemente la serie divergente más interesante porque simplemente no logra converger.

Sumas y series

Una serie infinita es una suma de infinitamente muchos términos y está escrita en la forma

$\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯.$

Pero, ¿qué significa esto? No podemos agregar un número infinito de términos de la misma manera que podemos agregar un número finito de términos. En cambio, el valor de una serie infinita se define en términos del límite de sumas parciales. Una suma parcial de una serie infinita es una suma finita de la forma

$\displaystyle \sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k.$

Para ver cómo utilizamos sumas parciales para evaluar series infinitas, considera el siguiente ejemplo. Supongamos que el petróleo se está filtrando en un lago tal que$1000$ galones ingresan al lago la primera semana. Durante la segunda semana, un$500$ galón adicional de petróleo ingresa al lago. A la tercera semana,$250$ más galones ingresan al lago. Supongamos que este patrón continúa de tal manera que cada semana la mitad de petróleo ingresa al lago como lo hizo la semana anterior. Si esto continúa para siempre, ¿qué podemos decir de la cantidad de petróleo en el lago? ¿La cantidad de petróleo seguirá siendo arbitrariamente grande, o es posible que se acerque a alguna cantidad finita? Para responder a esta pregunta, observamos la cantidad de petróleo en el lago después de$k$ semanas. Dejando$S_k$ denotar la cantidad de petróleo en el lago (medido en miles de galones) después de$k$ semanas, vemos que

$S_1=1$

$S_2=1+0.5=1+\frac{1}{2}$

$S_3=1+0.5+0.25=1+\frac{1}{2}+\frac{1}{4}$

$S_4=1+0.5+0.25+0.125=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}$

$S_5=1+0.5+0.25+0.125+0.0625=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}.$

Al observar este patrón, vemos que la cantidad de petróleo en el lago (en miles de galones) después de$k$ semanas es

$$S_k=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯+\frac{1}{2^{k−1}}=\sum_{n=1}^k\left(\frac{1}{2}\right)^{n−1}. \nonumber$$

Nos interesa lo que sucede como$k→∞.$ Simbólicamente, la cantidad de petróleo en el lago como$k→∞$ lo da la serie infinita

$$\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯. \nonumber$$

Al mismo tiempo, como$k→∞$, la cantidad de petróleo en el lago se puede calcular mediante la evaluación$\displaystyle \lim_{k→∞}S_k$. Por lo tanto, el comportamiento de la serie infinita se puede determinar observando el comportamiento de la secuencia de sumas parciales${S_k}$. Si la secuencia de sumas parciales${S_k}$ converge, decimos que la serie infinita converge, y su suma viene dada por$\displaystyle \lim_{k→∞}S_k$. Si la secuencia${S_k}$ diverge, decimos que la serie infinita diverge. Pasamos ahora nuestra atención a determinar el límite de esta secuencia${S_k}$.

Primero, simplificando algunas de estas sumas parciales, vemos que

$S_1=1$

$S_2=1+\frac{1}{2}=\frac{3}{2}$

$S_3=1+\frac{1}{2}+\frac{1}{4}=\frac{7}{4}$

$S_4=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{15}{8}$

$S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.$

Trazando algunos de estos valores en la Figura, parece que la secuencia${S_k}$ podría estar acercándose a 2.

Figura$\PageIndex{1}$: La gráfica muestra la secuencia de sumas parciales${S_k}$. Parece que la secuencia se acerca al valor$2$.

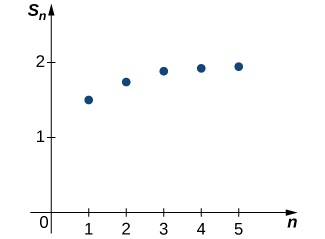
Busquemos pruebas más convincentes. En la siguiente tabla, enumeramos los valores de$S_k$ para varios valores de$k$.

$k$	5	10	15	20
$S_k$	1.9375	1.998	1.999939	1.999998

Estos datos aportan más evidencia que sugiere que la secuencia${S_k}$ converge a$2$. Posteriormente proporcionaremos un argumento analítico que se puede utilizar para demostrarlo$\displaystyle \lim_{k→∞}S_k=2$. Por ahora, confiamos en los datos numéricos y gráficos para convencernos de que la secuencia de sumas parciales realmente converge a$2$. Como esta secuencia de sumas parciales converge a$2$, decimos que la serie infinita converge$2$ y escribe

$$\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber$$

Volviendo a la pregunta sobre el petróleo en el lago, ya que esta serie infinita converge a$2$, concluimos que la cantidad de petróleo en el lago se acercará arbitrariamente a$2000$ galones ya que la cantidad de tiempo se vuelve suficientemente grande.

Esta serie es un ejemplo de una serie geométrica. Discutimos las series geométricas con más detalle más adelante en esta sección. En primer lugar, resumimos lo que significa que una serie infinita converja.

Definición

Una serie infinita es una expresión de la forma

$$\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber$$

Por cada entero positivo$k$, la suma

$$S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber$$

se llama la suma$k^{\text{th}}$ parcial de la serie infinita. Las sumas parciales forman una secuencia${S_k}$. Si la secuencia de sumas parciales converge a un número real$S$, la serie infinita converge. Si podemos describir la convergencia de una serie a$S$, llamamos a$S$ la suma de la serie, y escribimos

$$\sum_{n=1}^∞a_n=S. \nonumber$$

Si la secuencia de sumas parciales diverge, tenemos la divergencia de una serie.

Tenga en cuenta que el índice para una serie no necesita comenzar con$n=1$, sino que puede comenzar con cualquier valor. Por ejemplo, la serie

$$\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber$$

también se puede escribir como

$$\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber$$

Muchas veces es conveniente que el índice comience en$1$, así que si por alguna razón comienza en un valor diferente, podemos reindexar haciendo un cambio de variables. Por ejemplo, considere la serie

$$\sum_{n=2}^∞\frac{1}{n^2}. \nonumber$$

Al introducir la variable$m=n−1$, para que$n=m+1,$ podamos reescribir la serie como

$$\sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber$$

Ejemplo$\PageIndex{1}$: Evaluating Limits of Sequences of Partial Sums

Para cada una de las siguientes series, utilice la secuencia de sumas parciales para determinar si la serie converge o diverge.

1. $\displaystyle \sum_{n=1}^∞\frac{n}{n+1}$
2. $\displaystyle \sum_{n=1}^∞(−1)^n$
3. $\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}$

Solución

a. La secuencia de sumas parciales${S_k}$ satisface

$S_1=\dfrac{1}{2}$

$S_2=\dfrac{1}{2}+\dfrac{2}{3}$

$S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}$

$S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}$.

Observe que cada término agregado es mayor que$1/2$. Como resultado, vemos que

$S_1=\dfrac{1}{2}$

$S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)$

$S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)$

$S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).$

A partir de este patrón podemos ver eso$S_k>k\left(\frac{1}{2}\right)$ por cada entero$k$. Por lo tanto,${S_k}$ es sin límites y en consecuencia, diverge. Por lo tanto, la serie infinita$\displaystyle \sum^∞_{n=1}\frac{n}{n+1}$ diverge.

b. La secuencia de sumas parciales${S_k}$ satisface

$S_1=−1$

$S_2=−1+1=0$

$S_3=−1+1−1=−1$

$S_4=−1+1−1+1=0.$

A partir de este patrón podemos ver que la secuencia de sumas parciales es

$${S_k}={−1,0,−1,0,…}. \nonumber$$

Dado que esta secuencia diverge, la serie infinita$\displaystyle \sum^∞_{n=1}(−1)^n$ diverge.

c. La secuencia de sumas parciales${S_k}$ satisface

$S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}$

$S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}$

$S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}$

$S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}$

$S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.$

A partir de este patrón, podemos ver que la suma$k^{\text{th}}$ parcial viene dada por la fórmula explícita

$$S_k=\frac{k}{k+1} \nonumber$$ .

Desde que$k/(k+1)→1,$ concluimos que la secuencia de sumas parciales converge, y por lo tanto la serie infinita converge a$1$. Tenemos

$$\sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber$$

Ejercicio$\PageIndex{1}$

Determinar si la serie$\displaystyle \sum^∞_{n=1}\frac{n+1}{n}$ converge o diverge.

Pista

Mira la secuencia de sumas parciales.

Responder

La serie diverge porque la suma$k^{\text{th}}$ parcial$S_k>k$.

La serie armónica

Una serie útil para conocer es la serie armónica. La serie armónica se define como

$$\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber$$

Esta serie es interesante porque diverge, pero diverge muy lentamente. Con esto queremos decir que los términos en la secuencia de sumas parciales se${S_k}$ acercan al infinito, pero lo hacen muy lentamente. Mostraremos que la serie diverge, pero primero ilustramos el lento crecimiento de los términos en la secuencia${S_k}$ en la siguiente tabla.

$k$	10	100	1000	10,00	100,000	1,000,000
$S_k$	2.92897	5.18738	7.48547	9.78761	12.09015	14.39273

Incluso después de$1,000,000$ términos, la suma parcial sigue siendo relativamente pequeña. De esta tabla, no está claro que esta serie realmente diverja. Sin embargo, podemos demostrar analíticamente que la secuencia de sumas parciales diverge, y por lo tanto la serie diverge.

Para demostrar que la secuencia de sumas parciales diverge, mostramos que la secuencia de sumas parciales no tiene límites. Comenzamos por escribir las primeras sumas parciales varias:

$S_1=1$

$S_2=1+\dfrac{1}{2}$

$S_3=1+\dfrac{1}{2}+\dfrac{1}{3}$

$S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}$.

Observe que para los dos últimos términos en$S_4$,

$$\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber$$

Por lo tanto, concluimos que

$$S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber$$

Usando la misma idea para$S_8$, vemos que

$\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right)$.

A partir de este patrón, vemos que$S_1=1, S_2=1+1/2, S_4>1+2(1/2),$ y$S_8>1+3(1/2)$. De manera más general, se puede demostrar que$S_{2^j}>1+j(1/2)$ para todos$j>1$. Ya que$1+j(1/2)→∞,$ concluimos que la secuencia${S_k}$ es ilimitada y por lo tanto diverge. En el apartado anterior, afirmamos que las secuencias convergentes están acotadas. En consecuencia, dado${S_k}$ que no tiene límites, diverge. Así, la serie armónica diverge.

Propiedades algebraicas de la serie convergente

Dado que la suma de una serie infinita convergente se define como un límite de una secuencia, las propiedades algebraicas para las series enumeradas a continuación siguen directamente de las propiedades algebraicas para las secuencias.

Nota$\PageIndex{1}$: Algebraic Properties of Convergent Series

Dejar$\displaystyle \sum_{n=1}^∞ a_n$ y$\displaystyle \sum_{n=1}^∞ b_n$ ser series convergentes. Entonces se mantienen las siguientes propiedades algebraicas.

i. La serie$\displaystyle \sum_{n=1}^∞(a_n+b_n)$ converge, y$\displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n.$ (Regla de suma)

ii. La serie$\displaystyle \sum_{n=1}^∞(a_n−b_n)$ converge, y$\displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n.$ (Regla de diferencia)

iii. Para cualquier número real$c$, la serie$\displaystyle \sum_{n=1}^∞ca_n$ converge, y$\displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n$. (Regla Múltiple Constante)

Ejemplo$\PageIndex{2}$: Using Algebraic Properties of Convergent Series

Evaluar$\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].$

Solución

Demostramos anteriormente que

$$\sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber$$

y

$$\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber$$

Dado que ambas series convergen, podemos aplicar las propiedades de Note$\PageIndex{1}$ para evaluar

$$\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber$$

Usando la regla de suma, escriba

$\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.$

Entonces, usando la regla múltiple constante y las sumas anteriores, podemos concluir que

$\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.$

Ejercicio$\PageIndex{2}$

Evaluar$\displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}$.

Pista

Reescribir como$\displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}$.

Responder

10

Serie Geométrica

Una serie geométrica es cualquier serie que podamos escribir en la forma

$$a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber$$

Debido a que la relación de cada término en esta serie con respecto al término anterior es r, al número r se le llama la relación. Nos referimos a un como el término inicial porque es el primer término de la serie. Por ejemplo, la serie

$$\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber$$

es una serie geométrica con término inicial$a=1$ y relación$r=1/2$.

En general, ¿cuándo converge una serie geométrica? Considere la serie geométrica

$$\sum_{n=1}^∞ar^{n−1} \nonumber$$

cuando$a>0$. Su secuencia de sumas parciales${S_k}$ viene dada por

$$S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber$$

Considerar el caso cuando$r=1.$ En ese caso,

$$S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber$$

Ya que$a>0$, conocemos$ak→∞$ como$k→∞$. Por lo tanto, la secuencia de sumas parciales no tiene límites y, por lo tanto, diverge. En consecuencia, la serie infinita diverge para$r=1$. Para$r≠1$, para encontrar el límite de${S_k}$, multiplicar Ecuación por$1−r$. Al hacerlo, vemos que

$$(1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber$$

Todos los demás términos cancelan.

Por lo tanto,

$S_k=\dfrac{a(1−r^k)}{1−r}$para$r≠1$.

De nuestra discusión en el apartado anterior, sabemos que la secuencia geométrica$r^k→0$ si$|r|<1$ y que$r^k$ diverge si$|r|>1$ o$r=±1$. Por lo tanto, para$|r|<1, S_k→\dfrac{a}{1−r}$ y tenemos

$$\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber$$

Si$|r|≥1, S_k$ diverge, y por lo tanto

$$\sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber$$

Definiciones: Serie divergente y convergente

Una serie geométrica es una serie de la forma

$$\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \nonumber$$

Si$|r|<1$, la serie converge, y

$$\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber$$

Si$|r|≥1$, la serie diverge.

Las series geométricas a veces aparecen en formas ligeramente diferentes. Por ejemplo, a veces el índice comienza en un valor distinto de$n=1$ o el exponente implica una expresión lineal para$n$ otro que$n−1$. Siempre y cuando podamos reescribir la serie en la forma dada por Ecuación, se trata de una serie geométrica. Por ejemplo, considere la serie

$$\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber$$

Para ver que se trata de una serie geométrica, escribimos los primeros términos:

$\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.$

Vemos que el término inicial es$a=4/9$ y la relación es$r=2/3.$ Por lo tanto, la serie puede escribirse como

$\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.$

Ya que$r=2/3<1$, esta serie converge, y su suma viene dada por

$\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.$

Ejemplo$\PageIndex{3}$: Determining Convergence or Divergence of a Geometric Series

Determinar si cada una de las siguientes series geométricas converge o diverge, y si converge, encuentra su suma.

1. $\displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}$
2. $\displaystyle \sum^∞_{n=1}e^{2n}$

Solución

a. Escribiendo los primeros términos de la serie, tenemos

$$\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}$$

El término inicial$a=−3$ y la relación$r=−3/4$. Ya que$|r|=3/4<1$, la serie converge a

$$\frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber$$

b. Escribir esta serie como

$$e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber$$

podemos ver que esta es una serie geométrica donde$r=e^2>1.$ Por lo tanto, la serie diverge.

Ejercicio$\PageIndex{3}$

Determinar si la serie$\displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1}$ converge o diverge. Si converge, encuentra su suma.

Pista

$r=−2/5$

Responder

$5/7$

Ahora dirigimos nuestra atención a una agradable aplicación de series geométricas. Mostramos cómo se pueden usar para escribir decimales repetidos como fracciones de enteros.

Ejemplo$\PageIndex{4}$: Writing Repeating Decimals as Fractions of Integers

Usa una serie geométrica para escribir$3.\bar{26}$ como una fracción de enteros.

Solución

Desde$3.\bar{26}—=3.262626…,$ el principio escribimos

$$\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{1000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}$$

Ignorando el término 3, el resto de esta expresión es una serie geométrica con término inicial$a=26/10^2$ y relación$r=1/10^2.$ Por lo tanto, la suma de esta serie es

$$\frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber$$

Así,

$3.262626…=3+\frac{26}{99}=\frac{323}{99}$.

Ejercicio$\PageIndex{4}$

Escribir$5.2\bar{7}$ como una fracción de enteros.

Pista

Al expresar este número como una serie, encuentra una serie geométrica con término inicial$a=7/100$ y relación$r=1/10$.

Responder

$475/90$

Ejemplo$\PageIndex{5}$: Finding the Area of the Koch Snowflake

Defina una secuencia de figuras$\{F_n\}$ recursivamente de la siguiente manera (Figura$\PageIndex{2}$). Dejar$F_0$ ser un triángulo equilátero con lados de longitud$1$. Para$n≥1$, deja$F_n$ ser la curva creada quitando el tercio medio de cada lado de$F_{n−1}$ y reemplazándolo con un triángulo equilátero apuntando hacia afuera. La figura limitante como$n→∞$ se conoce como copo de nieve de Koch.

Figura$\PageIndex{2}$: Las cuatro primeras figuras,$F_0,F_1,F_2$, y$F_3$, en la construcción del copo de nieve de Koch.

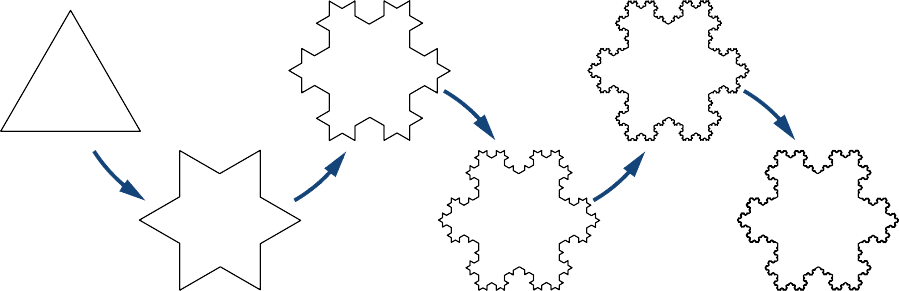
1. Encuentra la longitud$L_n$ del perímetro de$F_n$. $\displaystyle \lim_{n→∞}L_n$Evaluar para encontrar la longitud del perímetro del copo de nieve de Koch.
2. Encuentra el área$A_n$ de figura$F_n$. $\displaystyle \lim_{n→∞}A_n$Evaluar para encontrar el área del copo de nieve de Koch.

Solución

a. vamos a$N_n$ denotar el número de lados de la figura$F_n$. Ya que$F_0$ es un triángulo,$N_0=3$. Dejar ln denotar la longitud de cada lado de$F_n$. Dado que$F_0$ es un triángulo equilátero con lados de longitud$l_0=1$, ahora necesitamos determinar$N_1$ y$l_1$. Dado que$F_1$ se crea eliminando el tercio medio de cada lado y reemplazando ese segmento de línea con dos segmentos de línea, para cada lado de$F_0$, obtenemos cuatro lados adentro$F_1$. Por lo tanto, el número de lados para$F_1$ es

$N_1=4⋅3$.

Dado que la longitud de cada uno de estos nuevos segmentos de línea es$1/3$ la longitud de los segmentos de línea en$F_0$, la longitud de los segmentos de línea$F_1$ viene dada por

$l_1=\frac{1}{3}⋅1=\frac{1}{3}$.

Del mismo modo$F_2$, para, dado que el tercio medio de cada lado de$F_1$ se elimina y se reemplaza por dos segmentos de línea, el número de lados adentro$F_2$ viene dado por

$N_2=4N_1=4(4⋅3)=4^2⋅3.$

Dado que la longitud de cada uno de estos lados es$1/3$ la longitud de los lados de$F_1$, la longitud de cada lado de la figura$F_2$ viene dada por

$l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2$.

De manera más general, ya que$F_n$ se crea eliminando el tercio medio de cada lado de$F_{n−1}$ y reemplazando ese segmento de línea con dos segmentos de línea de longitud$\frac{1}{3}l_{n−1}$ en forma de triángulo equilátero, lo sabemos$N_n=4N_{n−1}$ y$l_n=\dfrac{l_{n−1}}{3}$. Por lo tanto, el número de lados de la figura$F_n$ es

$N_n=4^n⋅3$

y la longitud de cada lado es

$$l_n=\left(\frac{1}{3}\right)^n. \nonumber$$

Por lo tanto, para calcular el perímetro de$F_n$, multiplicamos el número de lados$N_n$ y la longitud de cada lado$l_n$. Concluimos que el perímetro de$F_n$ está dado por

$$L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber$$

Por lo tanto, la longitud del perímetro del copo de nieve de Koch es

$$L=\lim_{n→∞}L_n=∞. \nonumber$$

b. Dejar$T_n$ denotar el área de cada nuevo triángulo creado al formar$F_n$. For$n=0, T_0$ es el área del triángulo equilátero original. Por lo tanto,$T_0=A_0=\sqrt{3}/4$. Porque$n≥1$, dado que las longitudes de los lados del nuevo triángulo son$1/3$ la longitud de los lados de$F_{n−1}$, tenemos

$$T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber$$

Por lo tanto,$T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}$. Dado que se forma un nuevo triángulo a cada lado de$F_{n−1}$,

$$A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber$$

Escribiendo los primeros términos$A_0,A_1,A_2,$ vemos que

$A_0=\frac{\sqrt{3}}{4}$

$A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]$

$A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2]$.

De manera más general,

$A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right]$.

$4/9$Factorizando cada término dentro de los paréntesis internos, reescribimos nuestra expresión como

$A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right]$.

La expresión$1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}$ es una suma geométrica. Como se indicó anteriormente, esta suma satisface

$1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.$

Sustituyendo esta expresión por la expresión anterior y simplificando, concluimos que

$$A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber$$

Por lo tanto, la zona del copo de nieve de Koch es

$\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.$

Análisis

El copo de nieve de Koch es interesante porque tiene área finita, pero perímetro infinito. Si bien en un principio esto puede parecer imposible, recuerde que ya ha visto ejemplos similares anteriormente en el texto. Por ejemplo, considere la región delimitada por la curva$y=1/x^2$ y el$x$ eje -en el intervalo$[1,∞).$ Desde la integral impropia

$$∫^∞_1\frac{1}{x^2}\,dx \nonumber$$

converge, el área de esta región es finita, a pesar de que el perímetro es infinito.

Serie telescópica

Considera la serie$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.$ Discutimos esta serie en Ejemplo, mostrando que la serie converge escribiendo las primeras varias sumas parciales$S_1,S_2,…,S_6$ y notando que todas son de la forma$S_k=\dfrac{k}{k+1}$. Aquí utilizamos una técnica diferente para demostrar que esta serie converge. Mediante el uso de fracciones parciales, podemos escribir

$$\frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber$$

Por lo tanto, la serie se puede escribir como

$\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1+\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.$

Escribiendo los primeros varios términos en la secuencia de sumas parciales${S_k},$ vemos que

$S_1=1−\frac{1}{2}$

$S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}$

$S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}$.

En general,

$S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}$.

Notamos que los términos intermedios se cancelan entre sí, dejando solo el primer y último término. En cierto sentido, la serie colapsa como un spyglass con tubos que desaparecen entre sí para acortar el telescopio. Por esta razón, llamamos a una serie que tiene esta propiedad una serie telescópica. Para esta serie, desde$S_k=1−1/(k+1)$ y$1/(k+1)→0$ como$k→∞$, la secuencia de sumas parciales converge a$1$, y por lo tanto la serie converge a$1$.

Definición

Una serie telescópica es una serie en la que la mayoría de los términos cancelan en cada una de las sumas parciales, dejando sólo algunos de los primeros términos y algunos de los últimos términos.

Por ejemplo, cualquier serie del formulario

$\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯$

es una serie telescópica. Esto lo podemos ver escribiendo algunas de las sumas parciales. En particular, vemos que

$S_1=b_1−b_2$

$S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3$

$S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.$

En general, la késima suma parcial de esta serie es

$S_k=b_1−b_{k+1}$.

Dado que la késima suma parcial puede simplificarse a la diferencia de estos dos términos, la secuencia de sumas parciales${S_k}$ convergerá si y sólo si la secuencia${b_{k+1}}$ converge. Además, si la secuencia$b_{k+1}$ converge a algún número finito B, entonces la secuencia de sumas parciales converge a$b_1−B$, y por lo tanto

$\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.$

En el siguiente ejemplo, mostramos cómo utilizar estas ideas para analizar una serie telescópica de esta forma.

Ejemplo$\PageIndex{6}$: Evaluating a Telescoping Series

Determinar si la serie telescópica

$\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]$

converge o diverge. Si converge, encuentra su suma.

Solución

Al escribir términos en la secuencia de sumas parciales, podemos ver que

$S_1=\cos(1)−\cos(\frac{1}{2})$

$S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})$

$S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))$

$=\cos(1)−\cos(\frac{1}{4})$.

En general,

$S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right)$.

Ya que$1/(k+1)→0$ como$k→∞$ y$\cos x$ es una función continua,$\cos(1/(k+1))→\cos(0)=1$. Por lo tanto, concluimos que$S_k→\cos(1)−1$. La serie telescópica converge y la suma viene dada por

$\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.$

Ejercicio$\PageIndex{5}$

Determinar si$\displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}]$ converge o diverge. Si converge, encuentra su suma.

Pista

Escribe la secuencia de sumas parciales para ver qué términos cancelan.

Responder

$e−1$

Constante de Euler

Hemos demostrado que la serie armónica$\displaystyle \sum^∞_{n=1}\frac{1}{n}$ diverge. Aquí investigamos el comportamiento de las sumas parciales$S_k$ como$k→∞.$ En particular, mostramos que se comportan como la función logaritmo natural al mostrar que existe una constante$γ$ tal que

$\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ$como$k→∞.$

Esta constante$γ$ se conoce como la constante de Euler.

1. Dejar$\displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right).$ Evaluar$T_k$ para diversos valores de$k$.

2. Para$T_k$ como se define en la parte 1. mostrar que la secuencia${T_k}$ converge mediante el uso de los siguientes pasos.

a. Mostrar que la secuencia${T_k}$ es monótona decreciente. (Pista: Mostrar que$\ln(1+1/k>1/(k+1))$

b. Demostrar que la secuencia${T_k}$ está delimitada por debajo de cero. (Pista: Expresar$\ln k$ como una integral definitiva.)

c. Utilizar el Teorema de Convergencia Monótona para concluir que la secuencia${T_k}$ converge. El límite$γ$ es la constante de Euler.

3. Ahora estime a qué distancia$T_k$ está$γ$ para un entero dado$k$. Demuéstralo$k≥1, 0<T_k−γ≤1/k$ mediante el uso de los siguientes pasos.

a. Demostrar que$\ln(k+1)−\ln k<1/k.$

b. Utilice el resultado de la parte a. para mostrar que para cualquier entero$k$,

$$T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber$$

c. Para cualquier número entero$k$ y$j$ tal que$j>k$,$T_k−T_j$ exprese como suma telescópica escribiendo

$$T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber$$

Utilice el resultado de la parte b. combinado con esta suma telescópica para concluir que

$$T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber$$

a. Aplicar el límite a ambos lados de la desigualdad en la parte c. para concluir que

$$T_k−γ≤\frac{1}{k}. \nonumber$$

e. Estimar$γ$ con una precisión dentro de 0.001.

---

Conceptos clave

• Dada la serie infinita

$\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯$

y la secuencia correspondiente de sumas parciales${S_k}$ donde

$\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k$,

la serie converge si y sólo si la secuencia${S_k}$ converge.

• La serie geométrica$\displaystyle \sum^∞_{n=1}ar^{n−1}$ converge si$|r|<1$ y diverge si$|r|≥1.$ For$|r|<1,$

$\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}$.

• La serie armónica

$\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯$

diverge.

• Una serie de la forma$\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯$ es una serie telescópica. La suma$k^{\text{th}}$ parcial de esta serie viene dada por$S_k=b_1−b_{k+1}$. La serie convergerá si y sólo si$\displaystyle \lim_{k→∞} b_{k+1}$ existe. En ese caso,

$\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1})$.

Ecuaciones Clave

• Serie armónica

$\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯$

• Suma de una serie geométrica

$\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}$para$|r|<1$

---

Glosario

convergencia de una serie

una serie converge si la secuencia de sumas parciales para esa serie converge

divergencia de una serie

una serie diverge si la secuencia de sumas parciales para esa serie diverge

serie geométrica

una serie geométrica es una serie que se puede escribir en la forma

$\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯$

serie armónica

la serie armónica toma la forma

$\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯$

serie infinita

una serie infinita es una expresión de la forma

$\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n$

suma parcial

la suma$kth$ parcial de la serie infinita$\displaystyle \sum^∞_{n=1}a_n$ es la suma finita

$\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k$

serie telescópica

una serie telescópica es aquella en la que la mayoría de los términos cancelan en cada una de las sumas parciales