13.2E: Ejercicios para la Sección 13.2

Última actualización
Guardar como PDF

Page ID: 116174

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Tomando Derivadas de Funciones Vectoriales

En las preguntas 1 a 10, computar la derivada de cada función valorada por vector.

1)$\vecs r(t)=t^3 \,\hat{\mathbf{i}}+3t^2 \,\hat{\mathbf{j}}+\dfrac{t^3}{6}\,\hat{\mathbf{k}}$

Contestar: $\vecs r'(t)= 3t^2 \,\hat{\mathbf{i}}+6t\,\hat{\mathbf{j}}+\frac{1}{2}t^2\,\hat{\mathbf{k}}$

2)$\vecs r(t)=\sin(t) \,\hat{\mathbf{i}}+\cos(t) \,\hat{\mathbf{j}}+e^t \,\hat{\mathbf{k}}$

3)$\vecs r(t)=e^{−t} \,\hat{\mathbf{i}}+\sin(3t) \,\hat{\mathbf{j}}+10 \sqrt{t} \,\hat{\mathbf{k}}$. Aquí se muestra un boceto de la gráfica. Observe la naturaleza periódica variable de la gráfica.

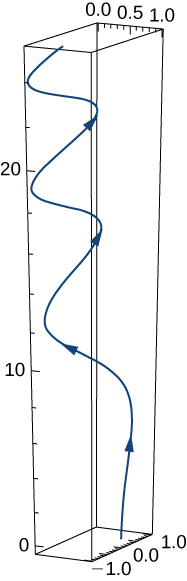
$Gráfica de la trayectoria del sacacorchos 3D de r (t) =e^ (−t) i + sin (3t) j+10 sqrt (t) k.$

Contestar: $\vecs r'(t) = −e^{−t}\,\hat{\mathbf{i}}+3\cos (3t)\,\hat{\mathbf{j}}+\dfrac{5}{\sqrt{t}}\,\hat{\mathbf{k}}$

4)$\vecs r(t)=e^t \,\hat{\mathbf{i}}+2e^t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

5)$\vecs r(t)=\,\hat{\mathbf{i}}+\,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

Contestar: $\vecs r'(t) = ⟨0,0,0⟩ = \vecs 0$

6)$\vecs r(t)=te^t \,\hat{\mathbf{i}}+t \ln(t) \,\hat{\mathbf{j}}+\sin(3t)\,\hat{\mathbf{k}}$

7)$\vecs r(t)=\left\langle\dfrac{1}{t+1},\,\arctan(t), \,\ln t^3 \right\rangle$

Contestar: $\vecs r'(t) = ⟨\dfrac{−1}{(t+1)^2},\dfrac{1}{1+t^2},\dfrac{3}{t}⟩$

8)$\vecs r(t)= \langle\tan 2t, \,\sec 2t, \,\sin ^2 t\rangle$

9)$\vecs r(t)=\langle 3,\, 4 \sin (3t),\, t \cos(t)\rangle$

Contestar: $\vecs r'(t) = ⟨0,12 \cos(3t), \cos t−t \sin t⟩$

10)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+te^{−2t} \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

11) a. Describir y esbozar la curva representada por la función vectorizada$\vecs r(t)=⟨6t,6t−t^2⟩$.

b. Localizar el punto más alto de la curva$\vecs r(t)=⟨6t,6t−t^2⟩$ y dar el valor de la función en este punto.

Contestar: b.$\vecs r(t)=⟨18,9⟩$ en$ t=3$

12) Encuentra las ecuaciones paramétricas de la línea tangente a la curva$\vecs r(t)=⟨t, t^2,t⟩$ en$t=2$.

13) Encuentra las ecuaciones paramétricas de la línea tangente a la curva$\vecs r(t)=⟨e^t,e^{−t},0⟩$ en$t=0$.

Contestar: $x=1+t,\quad y=1−t,\quad z=0$

14) Calcular la primera, segunda y tercera derivadas de$\vecs r(t)=3t \,\hat{\mathbf{i}}+6\ln(t) \,\hat{\mathbf{j}}+5e^{−3t}\,\hat{\mathbf{k}}$.

Describir el movimiento con funciones con valores vectoriales

En las preguntas 15 a 17, encuentre la velocidad y aceleración en los momentos dados, grafique la gráfica de la función de posición y dibuje los vectores de velocidad y aceleración en las ubicaciones correspondientes de la curva.

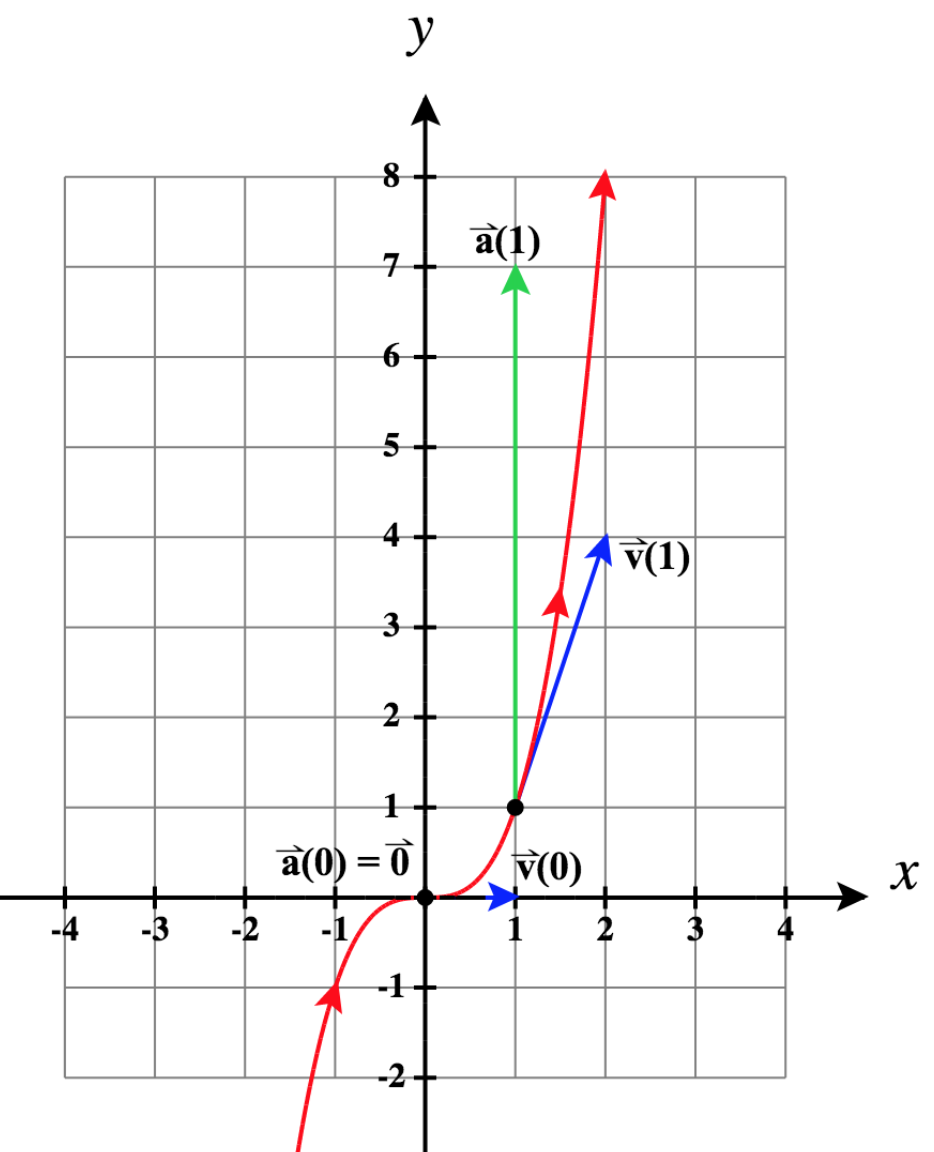
15)$\vecs r(t)= t \,\hat{\mathbf{i}}+t^3\,\hat{\mathbf{j}}$, en$t = 0$ y en$t = 1$

Contestar: \ (\ begin {array} {lll}\, & t = 0: & t = 1:\\
\ vecs r (t) = t\,\ mathbf {\ hat i} + t^3\,\ mathbf {\ hat j}, &\ vecs r (0) =\ vecs 0, &\ vecs r (1) =\ mathbf {\ hat i} +\ mathbf {\ hat j}\\
\ vecs v (t) =\ mathbf {\ hat i} + 3t^2\,\ mathbf {\ hat j}, &\ vecs v (0) =\ mathbf {\ hat i}, &\ vecs v (1) =\ mathbf {\ hat i} + 3\,\ mathbf {\ hat j}\
\ vecs a (t) = 6t\,\ mathbf {\ hat j}, &\ vecs a (0) =\ vecs 0, &\ vecs a (1) = 6\,\ mathbf {\ hat j}\ end {array}\)
$Trayectoria a lo largo del gráfico de y = x^3 de izquierda a derecha. También se muestran vectores de velocidad y aceleración a t = 0 y t = 1.$

16)$\vecs r(t)= \cos t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}}$, en$t = 0$, en$t = \frac{\pi}{4}$, y en$t = \frac{\pi}{2}$

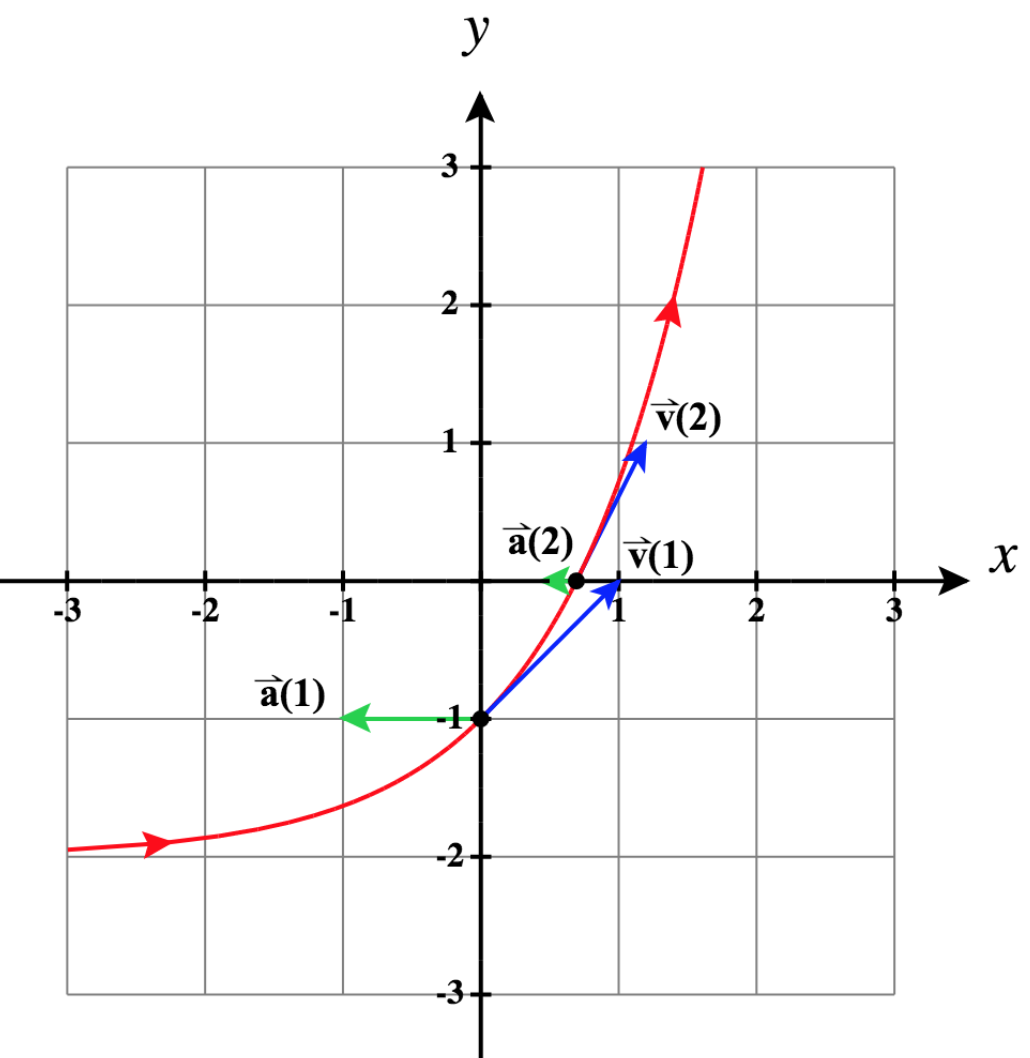
17)$\vecs r(t)= \ln t \,\hat{\mathbf{i}}+(t-2)\,\hat{\mathbf{j}}$, en$t = 1$ y en$t = 2$

Contestar: \ (\ begin {array} {lll}\, & t = 1: & t =2:\\
\ vecs r (t) = (\ ln t)\,\ mathbf {\ hat i} + (t - 2)\,\ mathbf {\ hat j}, &\ vecs r (1) = -\ mathbf {\ hat j}, &\ vecs r (2) = (\ ln 2)\,\ mathbf {\ hat i}\\
\ vecs v (t) =\ dfrac {1} {t}\,\ mathbf {\ hat i} +\ mathbf {\ hat j}, &\ vecs v (1) =\ mathbf {\ hat i} +\ mathbf {\ hat j}, &\ vecs v (2) =\ frac {1} {2}\ mathbf {\ hat i} +\ mathbf {\ hat j}\
\ vecs a (t) = -\ dfrac {1} {t^2}\,\ mathbf {\ hat i},\ mathbf {\ hat i}, &\ vecs a (1) = -\ mathbf {\ hat i}, &\ vecs a (2) = -\ frac {1} {4}\,\ mathbf {\ hat i}\ end {array}\)
$Trayectoria a lo largo de la gráfica de r (t) = ln (t) i + (t - 2) j. También se muestran los vectores de velocidad y aceleración a t = 1 y t = 2.$

En las preguntas 18 a 24, encuentra la velocidad, velocidad y aceleración de una partícula con la función de posición dada. Recuerde que la velocidad es la magnitud de la velocidad representada por$‖\vecs v(t)‖$ o$‖\vecs r′(t)‖$.

18)$\vecs r(t)=e^{2t} \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$

19)$\vecs r(t)=\cos t^3 \,\hat{\mathbf{i}}+\sin t^3 \,\hat{\mathbf{j}}$

Contestar: $\vecs v(t)=-3t^2\sin t^3 \,\hat{\mathbf{i}}+3t^2\cos t^3 \,\hat{\mathbf{j}}, \quad \text{speed}(t)=‖\vecs v(t)‖=3t^2, \quad \vecs a(t) = \left( -6t\sin t^3 - 9t^4\cos t^3 \right) \,\hat{\mathbf{i}}+\left( 6t\cos t^3 - 9t^4\sin t^3 \right) \,\hat{\mathbf{j}}$

20)$\vecs r(t)=⟨e^t,e^{−t},0⟩$

21)$\vecs r(t)=⟨t+ \cos t,t− \sin t⟩$

Contestar: $\vecs v(t)=⟨1− \sin t,1−\cos t⟩, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{3−2( \sin t+\cos t)}, \quad \vecs a(t) = ⟨- \cos t, \sin t⟩$

22)$\vecs r(t)=\dfrac{2t−1}{2t+1} \,\hat{\mathbf{i}}+\ln(1−4t^2) \,\hat{\mathbf{j}}$

23)$\vecs r(t)=\cos 3t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}} + 0.5t \,\hat{\mathbf{k}} $

Contestar: $\vecs v(t)=-3\sin 3t \,\hat{\mathbf{i}}+3\cos 3t \,\hat{\mathbf{j}} +0.5 \,\mathbf{\hat k}, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{9.25}\text{ units/sec}, \quad \vecs a(t) = -9\cos 3t \,\hat{\mathbf{i}}-9\sin 3t \,\hat{\mathbf{j}}$

24)$\vecs r(t)=e^{-t} \,\hat{\mathbf{i}}+(\ln t) \,\hat{\mathbf{j}}+(\sin 7t)\,\hat{\mathbf{k}}$

25) Considerar el vector de posición para que una partícula sea$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$. El gráfico se muestra aquí:

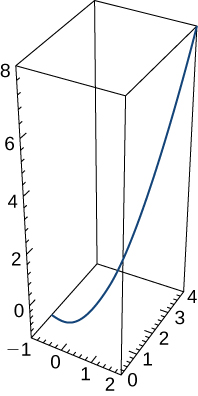
a. Encuentra el vector de velocidad en cualquier momento.

b. encontrar la velocidad de la partícula en el tiempo$t=2$ sec.

c. Encuentra la aceleración en el tiempo$t=2$ sec.

Contestar: a.$\vecs v(t)=\hat{\mathbf{i}}+2t\,\hat{\mathbf{j}}+3t^2 \,\hat{\mathbf{k}}$
b.$\sqrt{161}$ unidades/seg
Tenga en cuenta que$\text{speed}(t) = \|\vecs v(t)\| = \sqrt{1^2 + (2t)^2 + (3t^2)^2} = \sqrt{1 + 4t^2 + 9t^4}.$
Por lo tanto,$\text{speed}(2) = \sqrt{1 + 16 + 9(16)} = \sqrt{161}$ unidades/seg.
c. Desde$\vecs a(t)=2\,\hat{\mathbf{j}}+6t \,\hat{\mathbf{k}},$$\vecs a(2) = 2\,\hat{\mathbf{j}}+12 \,\hat{\mathbf{k}}$

26) Una partícula viaja a lo largo de la trayectoria de una elipse con la ecuación$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Encuentra lo siguiente:

a. Velocidad de la partícula

Contestar: $\vecs v(t)=⟨−\sin t,2 \cos t,0⟩$

b. Velocidad de la partícula a$t=\frac{π}{4}$

c. Aceleración de la partícula$t=\frac{π}{4}$

Contestar: $\vecs a(t)=⟨−\frac{\sqrt{2}}{2},−\sqrt{2},0⟩$

27) Mostrar que si la velocidad de una partícula que viaja a lo largo de una curva representada por una función de valor vectorial es constante, entonces la función de velocidad siempre es perpendicular a la función de aceleración.

Contestar: $\begin{align*} ‖\vecs v(t)‖ \; & = k \\ \vecs v(t)·\vecs v(t) \; & = k^2 \\ \frac{d}{dt}\Big(\vecs v(t)·\vecs v(t)\Big) \; & =\frac{d}{dt}\Big(k^2\Big)=0 \\ \vecs v(t)·\vecs v′(t)+\vecs v′(t)·\vecs v(t) \; & = 0 \\ 2\vecs v(t)·\vecs v′(t) \; & =0 \\ \vecs v(t)·\vecs v′(t) \; & = 0\end{align*}$

La última afirmación implica que la velocidad y la aceleración son perpendiculares u ortogonales.

28) Dada la función vectorizada$\vecs r(t)=⟨\tan t,\sec t,0⟩$ (aquí se muestra la gráfica), encuentra lo siguiente:

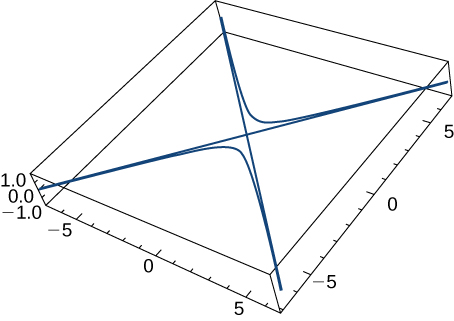
a. Velocidad

Contestar: $\vecs v(t)=\langle \sec ^2 t,\,\sec t \tan t\rangle$

b. velocidad

Contestar: $‖\vecs v(t)‖=\sqrt{\sec ^4 t+\sec ^2 t \tan ^2 t}=\sqrt{(\sec ^2 t)(\sec ^2 t+\tan ^2 t)}$

c. Aceleración

Contestar: $\vecs a(t)=\langle 2\sec ^2 t\tan t,\,\sec t \tan^2 t+\sec^3 t\rangle$

29) Encontrar la velocidad mínima de una partícula viajando a lo largo de la curva$\vecs r(t)=⟨t+\cos t,t−\sin t⟩$, donde$t∈[0,2π)$. Entonces también encuentra su velocidad máxima en este intervalo.

Contestar: La velocidad mínima es$\sqrt{3-2\sqrt{2}}\approx 0.41421$ cuando$t=\tfrac{\pi}{4}$.
Max. la velocidad es$\sqrt{3+2\sqrt{2}}\approx 2.41421$ cuando$t=\tfrac{5\pi}{4}$.

Para las preguntas 30 - 31, considere una partícula que se mueve en una trayectoria circular de radio$b$ según la función$\vecs r(t)=b \cos(\omega t) \,\hat{\mathbf{i}}+b\sin(\omega t) \,\hat{\mathbf{j}}$, donde$\omega$ está la velocidad angular,$\dfrac{d \theta}{dt}$.

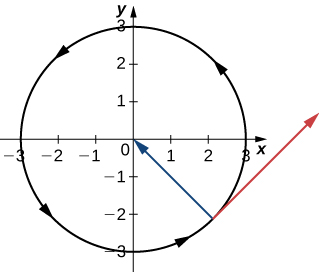
30) Mostrar que la velocidad de la partícula es proporcional a la velocidad angular.

31) Encuentra la función de velocidad y muestra que siempre$\vecs v(t)$ es ortogonal a$\vecs r(t)$.

Contestar: $\vecs r'(t)=−b \omega \sin( \omega t)\,\hat{\mathbf{i}}+b \omega \cos(\omega t)\,\hat{\mathbf{j}}$. Para mostrar ortogonalidad, tenga en cuenta que$\vecs r'(t)⋅\vecs r(t)=0$.

Suavidad de las funciones con valores vectoriales

Para las preguntas 32 a 40,

a. Determinar cualquier valor$t$ en el que no$\vecs r$ sea suave.

b. Determinar los intervalos abiertos en los que$\vecs r$ es suave.

c. Grafique la función vectorizada y describa su comportamiento en los puntos donde no sea suave.

32)$\vecs r(t) = \langle 3t, 5t^2 - 1\rangle$

33)$\vecs r(t)= t^3\,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}$

Contestar: a. no$\vecs r$ es suave en$t = 0$, ya que$\vecs r'(0) = \vecs 0$.
b.$\vecs r$ es suave en los intervalos abiertos$(-\infty, 0)$ y$(0, \infty)$.
c. Hay una cúspide cuando$t = 0$.

34)$\vecs r(t)=\langle 5,\, 2 \sin (t),\, \cos(t)\rangle$

35)$\vecs r(t) = \langle t^3 - 3t^2, 7\rangle$

Contestar: a. no$\vecs r$ es suave en$t = 0$ y$t = 2$, desde$\vecs r'(0) = \vecs 0$ y$\vecs r'(2) = \vecs 0$.
b.$\vecs r$ es suave en los intervalos abiertos$(-\infty, 0)$,$(0, 2)$, y$(2, \infty)$.
c. El movimiento en la curva se invierte a lo largo de la misma trayectoria en ambos$t = 0$ y$t = 2$.

36)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+t^3 \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

37)$\vecs r(t)=\left\langle \ln(t^2+4t+5), \,\dfrac{t^3}{3} - 4t,\, 5\right\rangle$

Contestar: a. no$\vecs r$ es suave en$t = -2$, ya que$\vecs r'(-2) = \vecs 0$.
Ya que el dominio de$\vecs r$ es$(-\infty, \infty)$, esto es todo lo que tenemos que eliminar.
b.$\vecs r$ es suave en los intervalos abiertos$(-\infty, -2)$ y$(-2, \infty)$.
c. Hay una cúspide cuando$t = -2$.

38)$\vecs r(t) = \left( 5\cos t - \cos 5t\right) \,\hat{\mathbf{i}} + \left( 5\sin t - \sin 5t \right) \,\hat{\mathbf{j}}$, para$0 \le t \le 2\pi$

39)$\vecs r(t)=\sqrt{t^3 + 9t^2} \,\hat{\mathbf{i}}+\left(t^2 +12t\right) \,\hat{\mathbf{j}}+7\,\hat{\mathbf{k}}$

Contestar: a. El dominio de$\vecs r$ es$[-9, \infty)$.
Y no$\vecs r$ es suave en$t = -6$, ya que$\vecs r'(-6) = \vecs 0$.
El dominio de$\vecs r'$ es$(-9, \infty)$, ya que$\vecs r'$ está indefinido en$t = -9$.
b.$\vecs r$ es suave en los intervalos abiertos$(-9, -6)$ y$(-6, \infty)$.
c. Hay una cúspide cuando$t = -6$.

40)$\vecs r(t)= \cos^3 t\,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$, para$0 \le t \le 2\pi$

Contestar: a. El dominio de$\vecs r$ es$(-\infty, \infty)$.
$\vecs r'(t) = -3(\cos^2 t)(\sin t)\,\hat{\mathbf{i}}+\cos t \,\hat{\mathbf{j}}$. Su dominio también lo es$(-\infty, \infty)$.
Pero tenga en cuenta que ambos componentes tienen un factor de$\cos t$, por lo que ambos componentes serán$0$ cuándo$\cos t = 0$.
Por lo tanto, no$\vecs r$ es suave en$t = \frac{\pi}{2}$ y en$t = \frac{3\pi}{2}$, desde$\vecs r'\left( \frac{\pi}{2}\right) = \vecs 0$ y$\vecs r'\left( \frac{3\pi}{2}\right) = \vecs 0$. Tenga en cuenta entonces que no$\vecs r$ es suave para ningún múltiplo impar de$\frac{\pi}{2}$, es decir para$t = \frac{(2n + 1)\pi}{2}$, para cualquier valor entero$n$.
b.$\vecs r$ es suave en los intervalos abiertos$\left(\dfrac{(2n - 1)\pi}{2}, \dfrac{(2n + 1)\pi}{2}\right)$, para cualquier valor entero$n$.
c. Hay una cúspide cuando$t = \dfrac{(2n + 1)\pi}{2}$, para cualquier valor entero$n$.

Propiedades de la Derivada

Para preguntas, 41 - 43, evaluar cada expresión dado que$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}−t^4 \,\hat{\mathbf{k}} $ y$\vecs s(t)=\sin(t) \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+ \cos(t) \,\hat{\mathbf{k}} $

41)$\dfrac{d}{dt}\big[\vecs r(t^2)\big]$

Contestar: $\dfrac{d}{dt}\big[\vecs r(t^2)\big] = ⟨2t,4t^3,−8t^7⟩$

42)$\dfrac{d}{dt}\big[t^2⋅\vecs s(t)\big]$

43)$\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]$

Contestar: $\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]=\sin t+2te^t−4t^3 \cos t+t\cos t+t^2e^t+t^4\sin t$

44) Encontrar$\vecs r'(t)⋅\vecs r''(t) \; for \; \vecs r(t)=−3t^5 \,\hat{\mathbf{i}}+5t \,\hat{\mathbf{j}}+2t^2 \,\hat{\mathbf{k}}$.

Contestar: $\vecs r'(t)⋅\vecs r''(t) = 900t^7+16t$

45) Dado$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$ y$\vecs u(t)=4t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$, encontrar$\frac{d}{dt}(\vecs r(t) \times \vecs u(t))$.

46) Evaluar$\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big]$ dado$\vecs u(t)=t^2 \,\hat{\mathbf{i}}−2t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

Contestar: $\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big] = 0 \,\hat{\mathbf{i}} +2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}$

47) Dado$\vecs r(t)=t \,\hat{\mathbf{i}}+2\sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$ y$\vecs u(t)=\dfrac{1}{t} \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$, encontrar lo siguiente:

a.$\vecs r(t) \times \vecs u(t)$

Contestar: $\vecs r(t) \times \vecs u(t) = \left\langle 0, \;2(\cos t)\left(\frac{1}{t}-t\right),\; 2 (\sin t)\left(t- \frac{1}{t}\right)\right\rangle$

b.$\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big)$

Contestar: $\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big) = \left\langle 0, \;2(\sin t)\left(t− \frac{1}{t}\right)−2 (\cos t)\left(1+ \frac{1}{t^2}\right),\;2 \left(\sin t\right)\left(1+ \frac{1}{t^2}\right)+2 \left(\cos t\right)\left(t−\frac{1}{t}\right)\right\rangle$

c. Ahora, use la regla del producto para la derivada del producto cruzado de dos vectores y muestre que este resultado es el mismo que la respuesta para el problema anterior.

Vectores de tangentes unitarios

Para las preguntas 48 - 51, encuentre un vector tangente unitario en el valor indicado de$t$.

48)$\vecs r(t)=3t^3 \,\hat{\mathbf{i}}+2t^2 \,\hat{\mathbf{j}}+\dfrac{1}{t} \,\hat{\mathbf{k}}; \quad t=1$

49)$\vecs r(t)=t \,\hat{\mathbf{i}}+\sin(2t) \,\hat{\mathbf{j}}+\cos(3t) \,\hat{\mathbf{k}}; \quad t=\frac{π}{3}$

Contestar: $\vecs r'\left(\frac{π}{3}\right) = \langle 1, \,-1,0\rangle$es un vector tangente, por lo que un vector tangente unitario sería:
$\frac{1}{\sqrt{2}}⟨1,−1,0⟩ \quad = \quad \langle \frac{\sqrt{2}}{2}, \,-\frac{\sqrt{2}}{2},\, 0\rangle$

50)$\vecs r(t)=\cos(2t) \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}};\quad t=\frac{π}{2}$

51)$\vecs r(t)=3e^t \,\hat{\mathbf{i}}+2e^{−3t} \,\hat{\mathbf{j}}+4e^{2t} \,\hat{\mathbf{k}}; \quad t= \ln(2)$

Contestar: $\vecs r'(\ln(2))= ⟨6,−\frac{3}{4},32⟩$es un vector tangente, por lo que un vector tangente unitario sería:
$\dfrac{1}{\sqrt{1060.5625}}\left\langle 6,−\frac{3}{4},32\right\rangle \quad = \quad \left\langle \dfrac{24\sqrt{16969}}{16969}, -\dfrac{12\sqrt{16969}}{67876}, \frac{128\sqrt{16969}}{16969}\right\rangle$

Para las preguntas 52 - 58, encuentre el vector tangente unitario$\vecs T(t)$ para las siguientes curvas parametrizadas.

52)$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$

53)$\vecs r(t)=6 \,\hat{\mathbf{i}}+\cos(3t) \,\hat{\mathbf{j}}+3\sin(4t) \,\hat{\mathbf{k}}, \quad 0≤t<2π$

Contestar: $\vecs T(t)=\dfrac{1}{\sqrt{9\sin ^2 (3t)+144\cos ^2 (4t)}}⟨0,−3\sin(3t),12\cos(4t)⟩$

54)$\vecs r(t)=⟨t \cos t,t \sin t⟩$

55)$\vecs r(t)=⟨t+1,2t+1,2t+2⟩$

Contestar: $\vecs T(t)=\frac{1}{3} ⟨1,2,2⟩$

56)$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+\sin t \,\hat{\mathbf{k}}, \quad 0≤t<2π$. Aquí se presentan dos vistas de esta curva:

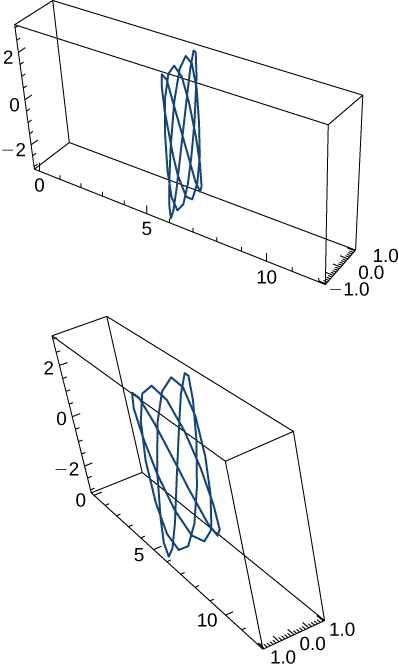
57)$\vecs r(t)=\left\langle t,\dfrac{1}{t}\right\rangle$. El gráfico se muestra aquí:

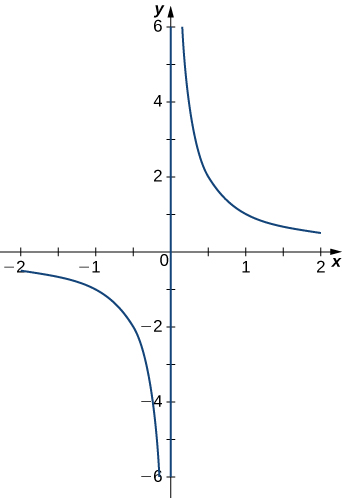
Contestar: $\vecs T(t)=\left\langle\dfrac{t^2}{\sqrt{t^4+1}},\frac{-1}{\sqrt{t^4+1}}\right\rangle$

58)$\vecs r(t)=3 \cos(4t) \,\hat{\mathbf{i}}+3 \sin(4t) \,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}},\quad 1 \le t \le 2$

Contestar: $\vecs T(t)=−\frac{12}{13} \sin(4t) \,\hat{\mathbf{i}}+ \frac{12}{13}\cos (4t) \,\hat{\mathbf{j}}+\frac{5}{13} \,\hat{\mathbf{k}}$

59) Una partícula viaja a lo largo de la trayectoria de una hélice con la ecuación$\vecs r(t)= \cos(t) \,\hat{\mathbf{i}}+\sin(t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}$. Vea la gráfica que se presenta aquí:

Encuentra lo siguiente:

a. Velocidad de la partícula en cualquier momento

Contestar: $\vecs v(t)=⟨−\sin t,\cos t,1⟩$

b. velocidad de la partícula en cualquier momento

c. Aceleración de la partícula en cualquier momento

Contestar: $\vecs a(t)=−\cos t \,\hat{\mathbf{i}}− \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$

d. Encuentra el vector tangente unitario para la hélice.

Integración de Funciones Vector-Valoradas

Evalúe las siguientes integrales:

60)$\displaystyle \int \left(e^t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+ \frac{1}{2t−1} \,\hat{\mathbf{k}}\right)\, dt$

61)$\displaystyle \int_0^1 \vecs r(t)\,dt$, donde$\vecs r(t)=\left\langle\sqrt[3]{t},\dfrac{1}{t+1},e^{−t}\right\rangle$

Contestar: $\frac{3}{4}\,\hat{\mathbf{i}}+\ln(2) \,\hat{\mathbf{j}}+(1−\frac{1}{e}) \,\hat{\mathbf{k}}$

62) Evaluar$\displaystyle \int_0^3‖t\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}‖dt$.

Contestar: $\frac{1}{3}(10^{\frac{3}{2}}−1)$

63) La función de aceleración, la velocidad inicial y la posición inicial de una partícula son

\[\begin{align*} \vecs a(t)&=−5 \cos t \,\hat{\mathbf{i}}−5\sin t \,\hat{\mathbf{j}}, \\ \vecs v(0)&=9 \,\hat{\mathbf{i}}+2 \,\hat{\mathbf{j}}, \quad \text{and} \\ \vecs r(0)&=5 \,\hat{\mathbf{i}} \end{align*}\]

Encontrar$\vecs v(t)$ y$\vecs r(t)$.

Contestar: $\vecs v(t) = \left(9 - 5\sin t\right)\,\hat{\mathbf{i}} + \left(-3 + 5\cos t\right)\,\hat{\mathbf{j}}$
$\vecs r(t) = \left(9t + 5\cos t\right)\,\hat{\mathbf{i}} + \left(-3t + 5\sin t\right)\,\hat{\mathbf{j}}$

64) Encontrar la antiderivada de$\vecs r'(t)=\cos(2t) \,\hat{\mathbf{i}}−2\sin t \,\hat{\mathbf{j}}+\dfrac{1}{1+t^2} \,\hat{\mathbf{k}}$ que satisfaga la condición inicial$\vecs r(0)=3 \,\hat{\mathbf{i}}−2 \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

65) Un objeto parte del reposo en el punto$P(1,2,0)$ y se mueve con una aceleración de$\vecs a(t)=\,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}}$, donde$‖\vecs a(t)‖$ se mide en pies por segundo por segundo por segundo. Encuentra la ubicación del objeto después del$t=2$ sec.

Colaboradores:

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created questions 11 - 19.