14.1E: Ejercicios para la Sección 14.1

Última actualización
Guardar como PDF

Page ID: 116227

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los siguientes ejercicios, evalúe cada función a los valores indicados.

1)$ W(x,y)=4x^2+y^2.$ Encontrar$ W(2,−1), W(−3,6)$.

Responder: $ W(2,−1) = 17,\quad W(−3,6) = 72$

2)$ W(x,y)=4x^2+y^2$. Encuentra$ W(2+h,3+h).$

3) El volumen de un cilindro circular derecho se calcula en función de dos variables,$ V(x,y)=πx^2y,$ donde$ x$ es el radio del cilindro circular derecho y$ y$ representa la altura del cilindro. Evaluar$ V(2,5)$ y explicar lo que esto significa.

Responder: $ V(2,5) = 20π\,\text{units}^3$Este es el volumen cuando el radio es$ 2$ y la altura es$ 5$.

4) Se construye un tanque de oxígeno de un cilindro derecho de altura$ y$ y radio$ x$ con dos hemisferios de radio$ x$ montados en la parte superior e inferior del cilindro. Expresar el volumen del cilindro en función de dos variables,$ x$ y$ y$, encontrar$ V(10,2)$, y explicar lo que esto significa.

Para los ejercicios 5 - 10, encuentre el dominio y el rango de la función dada. Indique el dominio en notación set-builder y el rango en notación de intervalo.

5)$ V(x,y)=4x^2+y^2$

Responder: Dominio: Es$\big\{(x, y) \, | \, x \in \rm I\!R, y \in \rm I\!R\big\}$ decir, todos los puntos en el$xy$ -plano
Rango:$ [0, \infty) $

6)$ f(x,y)=\sqrt{x^2+y^2−4}$

Responder: Dominio:$ \big\{(x, y) \, | \, x^2+y^2 \ge 4\big\}$
Rango:$ [0, \infty) $

7)$ f(x,y)=4\ln(y^2−x)$

Responder: Dominio:$ \big\{(x, y) \, | \, x<y^2 \big\}$
Rango:$ (-\infty, \infty) $

8)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Responder: Dominio:$ \big\{(x, y) \, | \, \dfrac{x^2}{4} + \dfrac{y^2}{16} \le 1\big\}$
Rango:$ [0, 4] $

9)$ z=\arccos(y−x)$

Responder: Dominio: Es$ \big\{(x, y) \, | \, x - 1 \le y \le x + 1\big\}$ decir, todos los puntos entre las gráficas de$y = x -1$ y$y = x +1 $.
Rango:$ [0, \pi] $

10)$ f(x,y)=\dfrac{y+2}{x^2}$

Responder: Dominio:$ \big\{(x, y) \, | \, x\neq 0 \big\}$
Rango:$ (-\infty, \infty) $

Encuentra el rango de las funciones.

11)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Responder: $ \big\{z \, | \, 0≤z≤4\big\}$o en notación de intervalo:$[0,4]$

12)$ V(x,y)=4x^2+y^2$

13)$ z=y^2−x^2$

Responder: El conjunto$\rm I\!R$

En los ejercicios 14 - 29, encuentra las curvas de nivel de cada función en los valores indicados de$ c$ para visualizar la función dada. Esboza una gráfica de contorno para aquellos ejercicios en los que te pidan más de 3 valores de$c$.

14)$ z(x,y)=y^2−x^2, \quad c=1$

15)$ z(x,y)=y^2−x^2,\quad c=4$

Responder: $ y^2−x^2=4,$una hipérbola

16)$ g(x,y)=x^2+y^2;\quad c=0, 1, 2, 3, 4, 9$

17)$ g(x,y)=4−x−y;\quad c=0,1, 2, 3, 4$

Responder: Las curvas de nivel son líneas con$ y = -x + (4 - c) $.
Por cada valor de$c$ estos son:
$ c = 0: \, y = -x + 4$,
$ c = 1: \, y = -x + 3$,
$ c = 2: \, y = -x + 2$,
$ c = 3: \, y = -x + 1$,
$ c = 4: \, y = -x $.
La gráfica de contorno consiste en una serie de líneas paralelas.
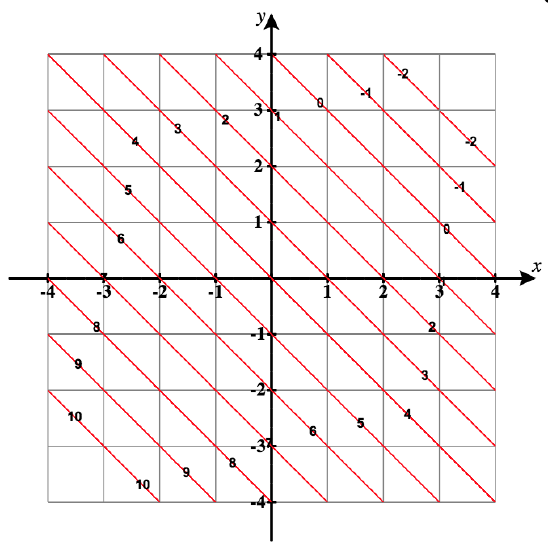
$Gráfica de contorno de la función g (x, y) =4−x−y$

18)$ f(x,y)=xy;c=1;\quad c=−1$

19)$ h(x,y)=2x−y;\quad c=-2,0,2$

Responder: $ 2x−y=0,2x−y=−2,2x−y=2;$tres líneas

20)$ f(x,y)=x^2−y;\quad c=1,2$

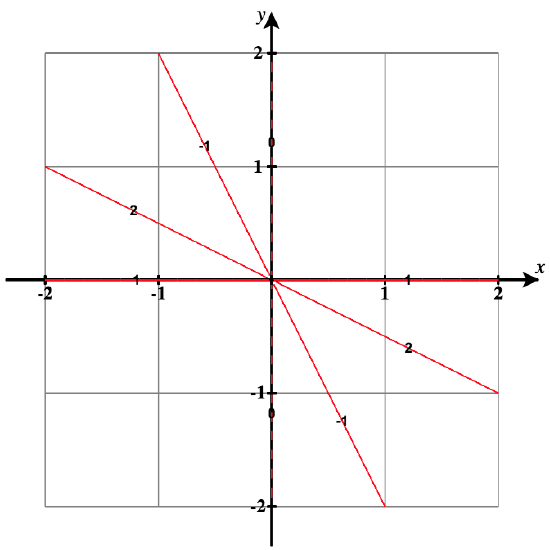
21)$ g(x,y)=\dfrac{x}{x+y};c=−1,0,1,2$

Responder: Las curvas de nivel son líneas con la forma$ y = x \left( \dfrac{1-c}{c} \right) $. En$c = 0$, lo resolvemos directamente de la ecuación$\dfrac{x}{x+y}=0$ para obtener$x = 0$.
Por cada valor de$c$ estos son:
$ c = -1: \, y = -2x$,
$ c = 0: \, x = 0,\text{ with }y \ne 0$,
$ c = 1: \, y = 0,\text{ with }x \ne 0$,
$ c = 2: \, y = -\frac{1}{2}x$.
$Gráfica de contorno de la función g (x, y) = x/ (x+y)$

22)$ g(x,y)=x^3−y;\quad c=−1,0,2$

23)$ g(x,y)=e^{xy};\quad c=\frac{1}{2},3$

Responder: Las curvas de nivel tienen la forma,$ y = \dfrac{\ln c}{x}$.
Para cada valor de$c$ estos son:
$ c = \frac{1}{2}: \, y = \dfrac{\ln \frac{1}{2}}{x}$ que se pueden reescribir como,$y = -\dfrac{\ln 2}{x}$

$ c = 3: \, y = \dfrac{\ln 3}{x}$.

24)$ f(x,y)=x^2;\quad c=4,9$

25)$ f(x,y)=xy−x;\quad c=−2,0,2$

Responder: Las curvas de nivel tienen la forma:$ y = \dfrac{c}{x} + 1$.
Aquí$y = \dfrac{-2}{x} + 1,\quad y = 1,\quad y = \dfrac{2}{x} + 1$ o$ xy−x=−2,\,xy−x=0,\,xy−x=2$

26)$ h(x,y)=\ln(x^2+y^2);\quad c=−1,0,1$

27)$ g(x,y)=\ln\left(\dfrac{y}{x^2}\right);\quad c=−2,0,2$

Responder: Las curvas de nivel tienen la forma,$ y =e^c x^2$.
Por cada valor de$c$ estos son:
$ c = -2: \, y = e^{-2} x^2 $,
$ c = 0: \, y = x^2 $,
$ c = 2: \, y = e^{2} x^2 $.

28)$ z=f(x,y)=\sqrt{x^2+y^2},\quad c=3$

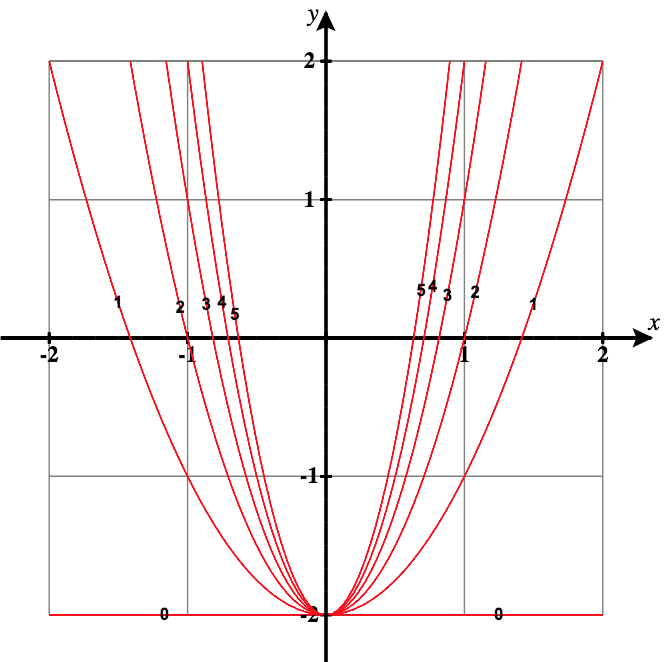
29)$ f(x,y)=\dfrac{y+2}{x^2},\quad c=$ cualquier constante

Responder: Las curvas de nivel son parábola de la forma$ y=cx^2−2,\text{ with }x \ne 0$.
$Gráfica de contorno de la función f (x, y) = (y + 2) /x^2$

En los ejercicios 30-32, encontrar las trazas verticales de las funciones en los valores indicados de$ x$ y$ y$, y trazar las trazas.

30)$ z=4−x−y, \quad x=2$

31)$ f(x,y)=3x+y^3, \quad x=1$

Responder

$ z=3+y^3,$una curva en el $zy$plano con reglas paralelas al$x$ eje

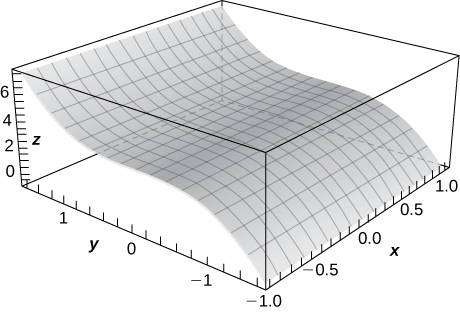
$Gráfica superficial de la función f (x, y) =3x+y^3$

32)$ z=\cos\sqrt{x^2+y^2}, \quad x=1$

En los ejercicios 33 - 38, encuentra el dominio y el rango de cada función.

33)$ z=\sqrt{100−4x^2−25y^2}$

Responder: Dominio:$ \big\{(x, y) \, | \, \dfrac{x^2}{25}+\dfrac{y^2}{4}≤1\big\}$
Rango:$ [0, 10] $

34)$ z=\ln(x−y^2)$

35)$ f(x,y,z)=\dfrac{1}{\sqrt{36−4x^2−9y^2−z^2}}$

Responder: Dominio:$ \big\{(x, y, z) \, | \, \dfrac{x^2}{9}+\dfrac{y^2}{4}+\dfrac{z^2}{36}<1\big\}$
Rango:$ \big[\frac{1}{6}, \infty\big) $

36)$ f(x,y,z)=\sqrt{49−x^2−y^2−z^2}$

37)$ f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}$

Responder: Dominio: Todos los puntos en$ xyz$ -espacio
Rango:$ \big(-\infty, \sqrt[3]{16}\,\big] $

38)$ f(x,y)=\cos\sqrt{x^2+y^2}$

En los ejercicios 39 - 40, trazar una gráfica de la función.

39)$ z=f(x,y)=\sqrt{x^2+y^2}$

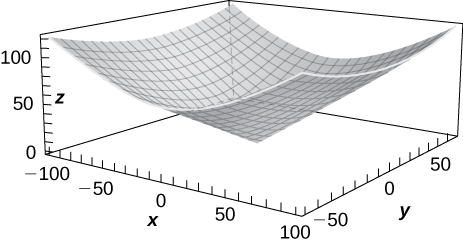
Responder: $Gráfica de superficie de la superficie f (x, y) =sqrt (x^2+y^2)$

40)$ z=x^2+y^2$

41) Utilizar la tecnología para graficar$ z=x^2y.$

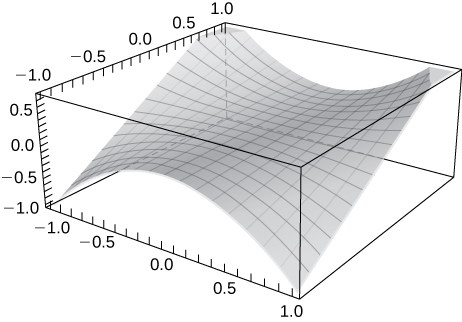
Responder: $Gráfica de superficie de la función z=x^2y$

En los ejercicios 42 - 46, bosquejar la función encontrando sus curvas de nivel. Verificar la gráfica usando tecnología, como CalcPlot3D.

42)$ f(x,y)=\sqrt{4−x^2−y^2}$

43)$ f(x,y)=2−\sqrt{x^2+y^2}$

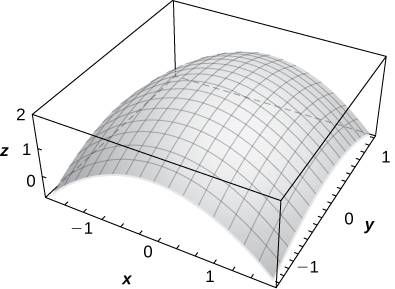
Responder: $Gráfica de superficie de la función f (x, y) =2−sqrt (x^2+y^2)$

44)$ z=1+e^{−x^2−y^2}$

45)$ z=\cos\sqrt{x^2+y^2}$

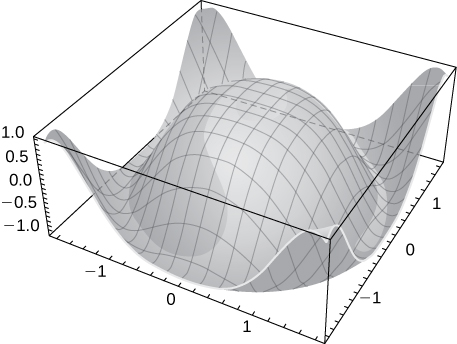
Responder: $Gráfica de superficie de la función z=cos (sqrt (x^2+y^2))$

46)$ z=y^2−x^2$

47) Describir las curvas de nivel para varios valores de$ c$$ z=x^2+y^2−2x−2y.$

Responder: Las curvas de nivel son círculos concéntricos centrados en el punto,$ (1, 1) $.
Puedes ver esto completando el cuadrado después de establecer esta función igual a$c$.
Es decir, escribimos$ x^2-2x+1+y^2−2y+1 = c + 2 $ lo que se puede reescribir como,$ (x - 1)^2 + (y - 1)^2 = c + 2 $.
Esto nos da círculos centrados en el punto,$ (1, 1) $, cada uno con un radio de$ \sqrt{c+2} $.

En los ejercicios, 48 - 52, encontrar la superficie nivelada para el valor dado de$c$ para cada función de tres variables y describirla.

48)$ w(x,y,z)=x−2y+z,\quad c=4$

49)$ w(x,y,z)=x^2+y^2+z^2,\quad c=9$

Responder: $ x^2+y^2+z^2=9$, una esfera de radio$ 3$

50)$ w(x,y,z)=x^2+y^2−z^2,\quad c=−4$

51)$ w(x,y,z)=x^2+y^2−z^2,\quad c=4$

Responder: $ x^2+y^2−z^2=4,$un hiperboloide de una hoja

52)$ w(x,y,z)=9x^2−4y^2+36z^2,\quad c=0$

En los ejercicios 53 - 55, encuentra una ecuación de la curva de nivel de la$ f$ que contiene el punto$ P$.

53)$ f(x,y)=1−4x^2−y^2,\quad P(0,1)$

Responder: $ 4x^2+y^2=1,$

54)$ g(x,y)=y^2\arctan x,\quad P(1,2)$

55)$ g(x,y)=e^{xy}(x^2+y^2),\quad P(1,0)$

Responder: $ 1=e^{xy}(x^2+y^2)$

56) La intensidad$ E$ de un campo eléctrico en el punto$ (x,y,z)$ resultante de un cable cargado infinitamente largo que se extiende a lo largo del$y$ eje viene dada por$ E(x,y,z)=k/\sqrt{x^2+y^2}$, donde$ k$ es una constante positiva. Para simplificar, deje$ k=1$ y encuentre las ecuaciones de las superficies niveladas para$ E=10$ y$ E=100.$

57) Una placa delgada hecha de hierro se ubica en el$xy$ -plano La temperatura$ T$ en grados Celsius en un punto$ P(x,y)$ es inversamente proporcional al cuadrado de su distancia desde el origen. $ T$Expresar en función de$ x$ y$ y$.

Responder: $ T(x,y)=\dfrac{k}{x^2+y^2}$

58) Refiérase al problema anterior. Usando la función de temperatura que se encuentra allí, determinar la constante de proporcionalidad si la temperatura en el punto$ P(1,2)$ es$ 50°C.$ Use esta constante para determinar la temperatura en el punto$ Q(3,4).$

59) Remítase al problema anterior. Encuentre las curvas de nivel para$ T=40°C$$ T=100°C,$ y describa lo que representan las curvas de nivel.

Responder: $ x^2+y^2=\dfrac{k}{40}, \quad x^2+y^2=\dfrac{k}{100}$. Las curvas de nivel representan círculos de radios$ \sqrt{10k}/20$ y$ \sqrt{k}/10$

Colaboradores

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added the contour plots to answers for problems 17, 21 and 29.