14.2: Límites y Continuidad

Objetivos de aprendizaje

• Calcular el límite de una función de dos variables.
• Aprenda cómo una función de dos variables puede acercarse a diferentes valores en un punto límite, dependiendo de la ruta de aproximación.
• Declarar las condiciones para la continuidad de una función de dos variables.
• Verificar la continuidad de una función de dos variables en un punto.
• Calcular el límite de una función de tres o más variables y verificar la continuidad de la función en un punto.

Ahora hemos examinado funciones de más de una variable y hemos visto cómo graficarlas. En esta sección, vemos cómo tomar el límite de una función de más de una variable, y lo que significa que una función de más de una variable sea continua en un punto de su dominio. Resulta que estos conceptos tienen aspectos que simplemente no ocurren con funciones de una variable.

Límite de una función de dos variables

Recordemos de la Sección 2.5 que la definición de un límite de una función de una variable:

Dejar\(f(x)\) definirse para todos\(x≠a\) en un intervalo abierto que contenga\(a\). \(L\)Déjese ser un número real. Entonces

\[\lim_{x→a}f(x)=L \nonumber \]

si por cada\(ε>0,\) existe un\(δ>0\), tal que si\(0<|x−a|<δ\) para todos\(x\) en el dominio de\(f\), entonces

\[|f(x)−L|<ε. \nonumber \]

Antes de poder adaptar esta definición para definir un límite de una función de dos variables, primero necesitamos ver cómo extender la idea de un intervalo abierto en una variable a un intervalo abierto en dos variables.

Definición:\(\delta\) Disks

Considerar un punto\((a,b)∈\mathbb{R}^2.\) Un\(δ\) disco centrado en el punto\((a,b)\) se define como un disco abierto de radio\(δ\) centrado en el punto\((a,b)\), es decir,

\[\{(x,y)∈\mathbb{R}^2∣(x−a)^2+(y−b)^2<δ^2\} \nonumber \]

como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un\(δ\) disco centrado alrededor del punto\((2,1)\).

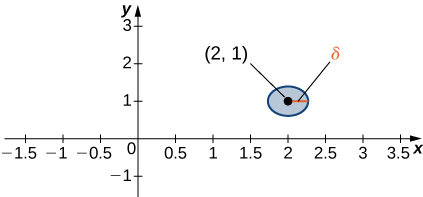
La idea de un\(δ\) disco aparece en la definición del límite de una función de dos variables. Si\(δ\) es pequeño, entonces todos los puntos\((x,y)\) en el\(δ\) disco están cerca\((a,b)\). Esto es completamente análogo a que x está cerca de a en la definición de un límite de una función de una variable. En una dimensión, expresamos esta restricción como

\[a−δ<a+δ.>/span>

En más de una dimensión, utilizamos un\(δ\) disco.

Definición: límite de una función de dos variables

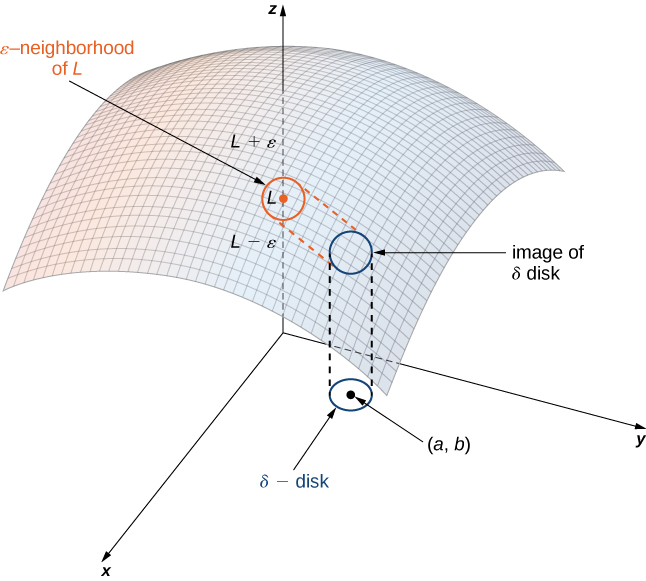
Dejar\(f\) ser una función de dos variables,\(x\) y\(y\). El límite de\(f(x,y)\) como\((x,y)\) enfoques\((a,b)\) es\(L\), escrito

\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]

si para cada uno\(ε>0\) existe un tamaño lo suficientemente pequeño\(δ>0\) como para que para todos los puntos\((x,y)\) en un\(δ\) disco alrededor\((a,b)\), excepto posiblemente por\((a,b)\) sí mismo, el valor de no\(f(x,y)\) esté más que\(ε\) alejado de\(L\) (Figura\(\PageIndex{2}\)).

Usando símbolos, escribimos lo siguiente: Para cualquiera\(ε>0\), existe un número\(δ>0\) tal que

\[|f(x,y)−L|<ε \nonumber \]

siempre que

\[0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]

Figura\(\PageIndex{2}\): El límite de una función que involucra dos variables requiere que\(f(x,y)\) estén dentro\(ε\) de\(L\) cuando\((x,y)\) esté dentro\(δ\) de\((a,b)\). Cuanto menor sea el valor de\(ε\), menor será el valor de\(δ\).

Demostrar que existe un límite usando la definición de un límite de una función de dos variables puede ser un desafío. En cambio, utilizamos el siguiente teorema, que nos da atajos para encontrar límites. Las fórmulas en este teorema son una extensión de las fórmulas en el teorema de las leyes de límite en Las leyes del límite.

Leyes de límite para funciones de dos variables

Dejar\(f(x,y)\) y\(g(x,y)\) definirse para todos\((x,y)≠(a,b)\) en un barrio alrededor\((a,b)\), y asumir que el barrio está contenido completamente dentro del dominio de\(f\). Supongamos que\(L\) y\(M\) son números reales tales que

\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]

y

\[\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber \]

y dejar que\(c\) sea una constante. Entonces cada una de las siguientes declaraciones sostiene:

Ley Constante:

\[\lim_{(x,y)→(a,b)}c=c \nonumber \]

Leyes de Identidad:

\[\lim_{(x,y)→(a,b)}x=a \nonumber \]

\[\lim_{(x,y)→(a,b)}y=b \nonumber \]

Ley de Suma:

\[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber \]

Ley de Diferencia:

\[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber \]

Ley Múltiple Constante:

\[\lim_{(x,y)→(a,b)}(cf(x,y))=cL \nonumber \]

Ley de Producto:

\[\lim_{(x,y)→(a,b)}(f(x,y)g(x,y))=LM \nonumber \]

Ley del cociente:

\[\lim_{(x,y)→(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{L}{M} \text{ for } M≠0 \nonumber \]

Ley del Poder:

\[\lim_{(x,y)→(a,b)}(f(x,y))^n=L^n \nonumber \]

para cualquier entero positivo\(n\).

Ley Raíz:

\[\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber \]

para todos\(L\) si\(n\) es impar y positivo, y para\(L≥0\) si n es par y positivo.

Las pruebas de estas propiedades son similares a las de los límites de funciones de una variable. Podemos aplicar estas leyes para encontrar límites de diversas funciones.

Ejemplo\(\PageIndex{1}\): Finding the Limit of a Function of Two Variables

Encuentra cada uno de los siguientes límites:

1. \(\displaystyle \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\)
2. \(\displaystyle \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y}\)

Solución

a. Primero use las leyes de suma y diferencia para separar los términos:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\\ = \left(\lim_{(x,y)→(2,−1)}x^2 \right)− \left(\lim_{(x,y)→(2,−1)}2xy \right)+ \left(\lim_{(x,y)→(2,−1)}3y^2 \right)−\left(\lim_{(x,y)→(2,−1)}4x\right) \\ + \left(\lim_{(x,y)→(2,−1)}3y \right)−\left(\lim_{(x,y)→(2,−1)}6\right). \end{align*}\]

A continuación, use la ley múltiple constante en los límites segundo, tercero, cuarto y quinto:

\[\begin{align*} =(\lim_{(x,y)→(2,−1)}x^2)−2(\lim_{(x,y)→(2,−1)}xy)+3(\lim_{(x,y)→(2,−1)}y^2)−4(\lim_{(x,y)→(2,−1)}x) \\[4pt] +3(\lim_{(x,y)→(2,−1)}y)−\lim_{(x,y)→(2,−1)}6.\end{align*}\]

Ahora bien, use la ley de poder en los límites primero y tercero, y la ley de producto en el segundo límite:

\[\begin{align*} \left(\lim_{(x,y)→(2,−1)}x\right)^2−2\left(\lim_{(x,y)→(2,−1)}x\right) \left(\lim_{(x,y)→(2,−1)}y\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)^2 \\ −4\left(\lim_{(x,y)→(2,−1)}x\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)−\lim_{(x,y)→(2,−1)}6. \end{align*}\]

Por último, utilizar las leyes de identidad sobre los seis primeros límites y la ley constante sobre el último límite:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6) = (2)^2−2(2)(−1)+3(−1)^2−4(2)+3(−1)−6 \\[4pt] =−6. \end{align*}\]

b. antes de aplicar la ley del cociente, es necesario verificar que el límite del denominador sea distinto de cero. Usando la ley de diferencia, la ley múltiple constante y la ley de identidad,

\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2,−1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}\]

Dado que el límite del denominador es distinto de cero, se aplica la ley del cociente. Ahora calculamos el límite del numerador usando la ley de diferencia, la ley múltiple constante y la ley de identidad:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}\]

Por lo tanto, según la ley del cociente tenemos

\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2,−1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. \end{align*}\]

Ejercicio\(\PageIndex{1}\):

Evalúe el siguiente límite:

\[\lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}. \nonumber \]

Pista

Utilice las leyes de límite.

Contestar

\[\displaystyle \lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}=\dfrac{3}{2} \nonumber \]

Ya que estamos tomando el límite de una función de dos variables, el punto\((a,b)\) está adentro\(\mathbb{R}^2\), y es posible acercarse a este punto desde un número infinito de direcciones. En ocasiones al calcular un límite, la respuesta varía dependiendo del camino que se tome hacia\((a,b)\). Si este es el caso, entonces el límite no existe. Es decir, el límite debe ser único, independientemente del camino que se tome.

Ejemplo\(\PageIndex{2}\): Limits That Fail to Exist

Demostrar que no existe ninguno de los siguientes límites:

1. \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{2xy}{3x^2+y^2}\)
2. \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4}\)

Solución

a. El dominio de la función\(f(x,y)=\dfrac{2xy}{3x^2+y^2}\) consiste en todos los puntos del\(xy\) plano, excepto el punto\((0,0)\) (Figura\(\PageIndex{3}\)). Para demostrar que el límite no existe como\((x,y)\) enfoques\((0,0)\), observamos que es imposible satisfacer la definición de un límite de una función de dos variables por el hecho de que la función toma diferentes valores a lo largo de diferentes líneas que pasan por punto\((0,0)\). Primero, considere la línea\(y=0\) en el\(xy\) -plano. Sustituir\(y=0\) en\(f(x,y)\) da

\[f(x,0)=\dfrac{2x(0)}{3x^2+0^2}=0 \nonumber \]

por cualquier valor de\(x\). Por lo tanto, el valor de\(f\) permanece constante para cualquier punto del\(x\) eje -y a medida que\(y\) se acerca a cero, la función permanece fija en cero.

A continuación, considere la línea\(y=x\). Sustituir\(y=x\) en\(f(x,y)\) da

\[f(x,x)=\dfrac{2x(x)}{3x^2+x^2}=\dfrac{2x^2}{4x^2}=\tfrac{1}{2}. \nonumber \]

Esto es cierto para cualquier punto de la línea\(y=x\). Si dejamos\(x\) acercarse a cero mientras permanecemos en esta línea, el valor de la función permanece fijo en\(\tfrac{1}{2}\), independientemente de lo pequeño\(x\) que sea.

Elija un valor para ε que sea menor que\(1/2\) —digamos,\(1/4\). Entonces, no importa cuán pequeño sea un\(δ\) disco que dibuje alrededor\((0,0)\), los valores de\(f(x,y)\) para los puntos dentro de ese\(δ\) disco incluirán ambos\(0\) y\(\tfrac{1}{2}\). Por lo tanto, la definición de límite en un punto nunca se satisface y el límite no existe.

Figura\(\PageIndex{3}\): Gráfico de la función\(f(x,y)=\dfrac{2xy}{3x^2+y^2}.\) A lo largo de la línea\(y=0\), la función es igual a cero; a lo largo de la línea\(y=x\), la función es igual a\(\tfrac{1}{2}\).

b. de manera similar a a., podemos acercarnos al origen a lo largo de cualquier línea recta que pase por el origen. Si intentamos el\(x\) -axis (i.e.,\(y=0\)), entonces la función permanece fija en cero. Lo mismo es cierto para el\(y\) eje -eje. Supongamos que nos acercamos al origen por una línea recta de pendiente\(k\). La ecuación de esta línea es\(y=kx\). Entonces el límite se convierte

\[\begin{align*} \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4x(kx)^2}{x^2+3(kx)^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4k^2x^3}{x^2+3k^4x^4} \\ =\lim_{(x,y)→(0,0)}\dfrac{4k^2x}{1+3k^4x^2} \\ = \dfrac{\displaystyle \lim_{(x,y)→(0,0)}(4k^2x)}{\displaystyle \lim_{(x,y)→(0,0)}(1+3k^4x^2)} \\ = 0. \end{align*}\]

independientemente del valor de\(k\). Parecería que el límite es igual a cero. ¿Y si elegimos una curva que pasa por el origen en su lugar? Por ejemplo, podemos considerar la parábola dada por la ecuación\(x=y^2\). Sustituir\(y^2\) en lugar de\(x\) en\(f(x,y)\) da

\[\begin{align*}\lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4(y^2)y^2}{(y^2)^2+3y^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4y^4}{y^4+3y^4} \\ = \lim_{(x,y)→(0,0)}1 \\ = 1. \end{align*}\]

Por la misma lógica en la parte a, es imposible encontrar un disco δ alrededor del origen que satisfaga la definición del límite para cualquier valor de\(ε<1.\) Por lo tanto,

\[\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} \nonumber \]

no existe.

Ejercicio\(\PageIndex{2}\):

Demostrar que

\[\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2} \nonumber \]

no existe.

Pista

Seleccionar una línea con pendiente\(k\) que pasa a través del punto\((2,1).\)

Contestar

Si\(y=k(x−2)+1,\) entonces\(\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2}=\dfrac{k}{1+k^2}\). Ya que la respuesta depende\(k,\) del límite no existe.

Puntos interiores y puntos de contorno

Para estudiar la continuidad y diferenciabilidad de una función de dos o más variables, primero necesitamos aprender alguna terminología nueva.

Definición: puntos interiores y límites

Dejar\(S\) ser un subconjunto de\(\mathbb{R}^2\) (Figura\(\PageIndex{4}\)).

1. Un punto\(P_0\) se llama punto interior de\(S\) si hay un\(δ\) disco centrado alrededor\(P_0\) contenido completamente adentro\(S\).
2. Un punto\(P_0\) se denomina punto límite de\(S\) si cada\(δ\) disco centrado alrededor\(P_0\) contiene puntos tanto dentro como fuera\(S\).

Figura\(\PageIndex{4}\): En el conjunto\(S\) mostrado,\((−1,1)\) es un punto interior y\((2,3)\) es un punto límite.

Definición: Juegos abiertos y cerrados

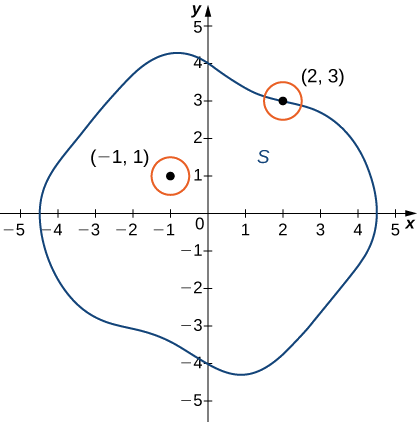
Dejar\(S\) ser un subconjunto de\(\mathbb{R}^2\) (Figura\(\PageIndex{4}\)).

1. \(S\)se llama un conjunto abierto si cada punto de\(S\) es un punto interior.
2. \(S\)se llama un conjunto cerrado si contiene todos sus puntos de límite.

Un ejemplo de un conjunto abierto es un\(δ\) disco. Si incluimos el límite del disco, entonces se convierte en un conjunto cerrado. Un conjunto que contiene algunos, pero no todos, de sus puntos límite no es ni abierto ni cerrado. Por ejemplo, si incluimos la mitad del límite de un\(δ\) disco pero no la otra mitad, entonces el conjunto no está abierto ni cerrado.

Definición: conjuntos conectados y regiones

Dejar\(S\) ser un subconjunto de\(\mathbb{R}^2\) (Figura\(\PageIndex{4}\)).

1. Un conjunto abierto\(S\) es un conjunto conectado si no se puede representar como la unión de dos o más subconjuntos abiertos no vacíos y disjuntos.
2. Un conjunto\(S\) es una región si está abierta, conectada y no vacía.

La definición de un límite de una función de dos variables requiere que el\(δ\) disco esté contenido dentro del dominio de la función. Sin embargo, si deseamos encontrar el límite de una función en un punto límite del dominio, el\(δ\) disco no está contenido dentro del dominio. Por definición, algunos de los puntos del\(δ\) disco están dentro del dominio y otros están afuera. Por lo tanto, solo necesitamos considerar los puntos que están dentro tanto del\(δ\) disco como del dominio de la función. Esto lleva a la definición del límite de una función en un punto límite.

Definición

Dejar\(f\) ser una función de dos variables,\(x\) y\(y\), y supongamos que\((a,b)\) está en el límite del dominio de\(f\). Entonces, el límite de\(f(x,y)\) como\((x,y)\) enfoques\((a,b)\) es\(L\), escrito

\[\lim_{(x,y)→(a,b)}f(x,y)=L, \nonumber \]

si para alguno\(ε>0,\) existe un número\(δ>0\) tal que para cualquier punto\((x,y)\) dentro del dominio de\(f\) y dentro de una distancia adecuadamente pequeña positiva\(δ\)\((a,b),\) del valor de no\(f(x,y)\) esté más que\(ε\) lejos de\(L\) (Figura\(\PageIndex{2}\)). Usando símbolos, podemos escribir: Para cualquiera\(ε>0\), existe un número\(δ>0\) tal que

\[|f(x,y)−L|<ε\, \text{whenever}\, 0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]

Ejemplo\(\PageIndex{3}\): Limit of a Function at a Boundary Point

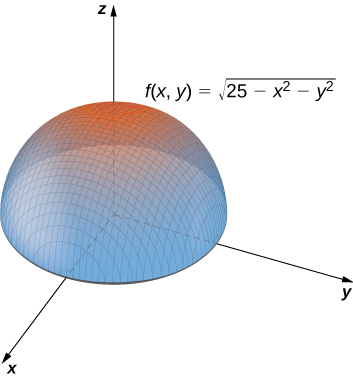
Demostrar

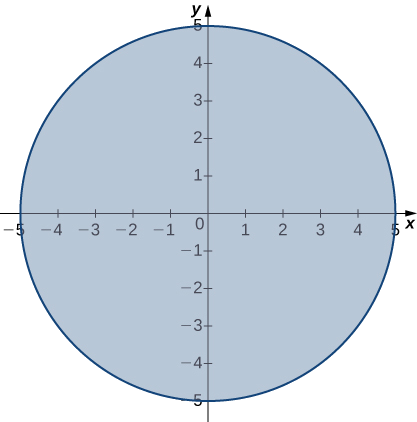
\[\lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2}=0. \nonumber \]

Solución

El dominio de la función\(f(x,y)=\sqrt{25−x^2−y^2}\) es\(\big\{(x,y)∈\mathbb{R}^2∣x^2+y^2≤25\big\}\), que es un círculo de radio\(5\) centrado en el origen, junto con su interior como se muestra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Dominio de la función\(f(x,y)=\sqrt{25−x^2−y^2}\).

Podemos usar las leyes de límite, que se aplican a los límites en el límite de dominios así como a los puntos interiores:

\[\begin{align*} \lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2} =\sqrt{\lim_{(x,y)→(4,3)}(25−x^2−y^2)} \\ = \sqrt{\lim_{(x,y)→(4,3)}25−\lim_{(x,y)→(4,3)}x^2−\lim_{(x,y)→(4,3)}y^2} \\ =\sqrt{25−4^2−3^2} \\ = 0 \end{align*}\]

Consulte la siguiente gráfica.

Figura\(\PageIndex{6}\): Gráfica de la función\(f(x,y)=\sqrt{25−x^2−y^2}\).

Ejercicio\(\PageIndex{3}\)

Evalúe el siguiente límite:

\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2}. \nonumber \]

Pista

Determinar el dominio de\(f(x,y)=\sqrt{29−x^2−y^2}\).

Contestar

\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2} \nonumber \]

Continuidad de Funciones de Dos Variables

En Continuidad, definimos la continuidad de una función de una variable y vimos cómo se basaba en el límite de una función de una variable. En particular, son necesarias tres condiciones\(f(x)\) para ser continuo en el punto\(x=a\)

1. \(f(a)\)existe.
2. \(\displaystyle \lim_{x→a}f(x)\)existe.
3. \(\displaystyle \lim_{x→a}f(x)=f(a).\)

Estas tres condiciones son necesarias para la continuidad de una función de dos variables también.

Definición: Funciones continuas

Una función\(f(x,y)\) es continua en un punto\((a,b)\) de su dominio si se cumplen las siguientes condiciones:

1. \(f(a,b)\)existe.
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)existe.
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)

Ejemplo\(\PageIndex{4}\): Demonstrating Continuity for a Function of Two Variables

Demostrar que la función

\[f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber \]

es continuo en el punto\((5,−3).\)

Solución

Hay tres condiciones a satisfacer, según la definición de continuidad. En este ejemplo,\(a=5\) y\(b=−3.\)

1. \(f(a,b)\)existe. Esto es cierto porque el dominio de la función f consiste en aquellos pares ordenados para los cuales el denominador es distinto de cero (i.e.,\(x+y+1≠0\)). Punto\((5,−3)\) satisface esta condición. Además,

\[f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6}{2+1}=3. \nonumber \]

2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)existe. Esto también es cierto:

\[\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,−3)}\dfrac{3x+2y}{x+y+1} \\ =\dfrac{\displaystyle \lim_{(x,y)→(5,−3)}(3x+2y)}{\displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align*}\]

3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)Esto es cierto porque acabamos de demostrar que ambos lados de esta ecuación equivalen a tres.

Ejercicio\(\PageIndex{4}\)

Demostrar que la función

\[f(x,y)=\sqrt{26−2x^2−y^2}\nonumber \]

es continuo en el punto\((2,−3)\).

Pista

Utilice la definición de continuidad en tres partes.

Contestar

1. El dominio de\(f\) contiene el par ordenado\((2,−3)\) porque\(f(a,b)=f(2,−3)=\sqrt{16−2(2)^2−(−3)^2}=3\)
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=3\)
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b)=3\)

La continuidad de una función de cualquier número de variables también se puede definir en términos de delta y épsilon. Una función de dos variables es continua\((x_0,y_0)\) en un punto de su dominio si por cada uno\(ε>0\) existe\(δ>0\) tal que, siempre que\(\sqrt{(x−x_0)^2+(y−y_0)^2}<δ\) sea verdad,\(|f(x,y)−f(a,b)|<ε.\) esta definición se puede combinar con la definición formal (es decir, la definición épsilon-delta) de continuidad de una función de una variable para probar los siguientes teoremas:

La suma de funciones continuas es continua

Si\(f(x,y)\) es continuo en\((x_0,y_0)\), y\(g(x,y)\) es continuo en\((x_0,y_0)\), entonces\(f(x,y)+g(x,y)\) es continuo en\((x_0,y_0)\).

El producto de las funciones continuas es continuo

Si\(g(x)\) es continuo en\(x_0\) y\(h(y)\) es continuo en\(y_0\), entonces\(f(x,y)=g(x)h(y)\) es continuo en\((x_0,y_0).\)

La composición de las funciones continuas es continua

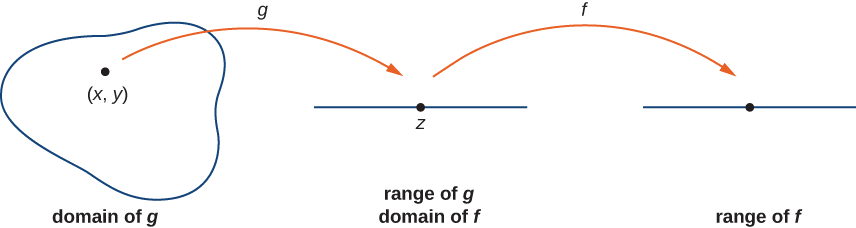
Dejar\(g\) ser una función de dos variables de un dominio\(D⊆\mathbb{R}^2\) a un rango\(R⊆R.\) Supongamos que\(g\) es continuo en algún momento\((x_0,y_0)∈D\) y definir\(z_0=g(x_0,y_0)\). Sea f una función que mapee\(R\) a\(R\) tal que\(z_0\) esté en el dominio de\(f\). Por último, supongamos que\(f\) es continuo en\(z_0\). Luego\(f∘g\) es continuo en\((x_0,y_0)\) como se muestra en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): La composición de dos funciones continuas es continua.

Ahora usemos los teoremas anteriores para mostrar la continuidad de las funciones en los siguientes ejemplos.

Ejemplo\(\PageIndex{5}\): More Examples of Continuity of a Function of Two Variables

Demostrar que las funciones\(f(x,y)=4x^3y^2\) y\(g(x,y)=\cos(4x^3y^2)\) son continuas en todas partes.

Solución

Los polinomios\(g(x)=4x^3\) y\(h(y)=y^2\) son continuos en cada número real, y por lo tanto, por el producto del teorema de funciones continuas,\(f(x,y)=4x^3y^2\) es continuo\((x,y)\) en cada punto del\(xy\) plano. Dado que\(f(x,y)=4x^3y^2\) es continuo\((x,y)\) en cada punto del\(xy\) plano y\(g(x)=\cos x\) es continuo en cada número real\(x\), la continuidad de la composición de funciones nos dice que\(g(x,y)=\cos(4x^3y^2)\) es continua\((x,y)\) en cada punto del\(xy\) plano.

Ejercicio\(\PageIndex{5}\)

Demostrar que las funciones\(f(x,y)=2x^2y^3+3\) y\(g(x,y)=(2x^2y^3+3)^4\) son continuas en todas partes.

Pista

Utilizar la continuidad de la suma, el producto y la composición de dos funciones.

Contestar

Los polinomios\(g(x)=2x^2\) y\(h(y)=y^3\) son continuos en cada número real; por lo tanto, por el producto del teorema de funciones continuas,\(f(x,y)=2x^2y^3\) es continuo\((x,y)\) en cada punto del\(xy\) plano. Además, cualquier función constante es continua en todas partes, por lo que\(g(x,y)=3\) es continua\((x,y)\) en cada punto del\(xy\) plano. Por lo tanto,\(f(x,y)=2x^2y^3+3\) es continuo\((x,y)\) en cada punto del\(xy\) -plano. Por último,\(h(x)=x^4\) es continuo en cada número real\(x\), por lo que por la continuidad de las funciones compuestas el teorema\(g(x,y)=(2x^2y^3+3)^4\) es continuo\((x,y)\) en cada punto del\(xy\) plano -plano.

Funciones de tres o más variables

El límite de una función de tres o más variables ocurre fácilmente en aplicaciones. Por ejemplo, supongamos que tenemos una función\(f(x,y,z)\) que da la temperatura en una ubicación física\((x,y,z)\) en tres dimensiones. O tal vez una función\(g(x,y,z,t)\) puede indicar presión de aire en una ubicación\((x,y,z)\) en el momento\(t\). ¿Cómo podemos tomar un límite en un punto de entrada\(\mathbb{R}^3\)? ¿Qué significa ser continuo en un punto en cuatro dimensiones?

Las respuestas a estas preguntas se basan en extender el concepto de\(δ\) disco a más de dos dimensiones. Entonces, las ideas del límite de una función de tres o más variables y la continuidad de una función de tres o más variables son muy similares a las definiciones dadas anteriormente para una función de dos variables.

Definición:\(δ\)-balls

Dejemos\((x_0,y_0,z_0)\) ser un punto en\(\mathbb{R}^3\). Entonces, una\(δ\) -bola en tres dimensiones consiste en todos los puntos en\(\mathbb{R}^3\) tumbarse a una distancia menor que\(δ\) de\((x_0,y_0,z_0)\) —es decir,

\[\big\{(x,y,z)∈\mathbb{R}^3∣\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]

Para definir una\(δ\) -bola en dimensiones superiores, agregue términos adicionales bajo el radical para corresponder a cada dimensión adicional. Por ejemplo, dado un punto\(P=(w_0,x_0,y_0,z_0)\) en\(\mathbb{R}^4\), una\(δ\) pelota alrededor\(P\) puede describirse mediante

\[\big\{(w,x,y,z)∈\mathbb{R}^4∣\sqrt{(w−w_0)^2+(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]

Para demostrar que existe un límite de una función de tres variables en un punto\((x_0,y_0,z_0)\), basta con mostrar que para cualquier punto de una\(δ\) bola centrada en\((x_0,y_0,z_0)\), el valor de la función en ese punto es arbitrariamente cercano a un valor fijo (el valor límite). Todas las leyes de límite para funciones de dos variables también se mantienen para funciones de más de dos variables.

Ejemplo\(\PageIndex{6}\): Finding the Limit of a Function of Three Variables

Encuentra

\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}. \nonumber \]

Solución

Antes de que podamos aplicar la ley del cociente, necesitamos verificar que el límite del denominador sea distinto de cero. Utilizando la ley de diferencia, la ley de identidad y la ley constante,

\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y)−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{align*}\]

Dado que esto es distinto de cero, a continuación encontramos el límite del numerador. Usando la ley de producto, la ley de poder, la ley de diferencia, la ley múltiple constante y la ley de identidad,

\[\begin{align*} \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z) =(\lim_{(x,y,z)→(4,1,−3)}x)^2(\lim_{(x,y,z)→(4,1,−3)}y)−3\lim_{(x,y,z)→(4,1,−3)}z \\ =(4^2)(1)−3(−3) \\ = 16+9 \\ = 25 \end{align*}\]

Por último, aplicando la ley del cociente:

\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}=\dfrac{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z)}{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(2x+5y−z)}=\dfrac{25}{16} \nonumber \]

Ejercicio\(\PageIndex{6}\)

Encuentra

\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2} \nonumber \]

Pista

Utilizar las leyes de límite y la continuidad de la composición de funciones.

Contestar

\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2}=2 \nonumber \]

Conceptos clave

• Para estudiar los límites y la continuidad de las funciones de dos variables, utilizamos un\(δ\) disco centrado alrededor de un punto dado.
• Una función de varias variables tiene un límite si para cualquier punto de una\(δ\) bola centrada en un punto\(P\), el valor de la función en ese punto es arbitrariamente cercano a un valor fijo (el valor límite).
• Las leyes límite establecidas para una función de una variable tienen extensiones naturales a funciones de más de una variable.
• Una función de dos variables es continua en un punto si el límite existe en ese punto, la función existe en ese punto, y el límite y la función son iguales en ese punto.

Glosario

punto límite

un punto\(P_0\) de\(R\) es un punto límite si cada\(δ\) disco centrado alrededor\(P_0\) contiene puntos tanto dentro como fuera\(R\)

conjunto cerrado

un conjunto\(S\) que contiene todos sus puntos de contorno

conjunto conectado

un conjunto abierto\(S\) que no se puede representar como la unión de dos o más subconjuntos abiertos no vacíos y disjuntos

\(δ\)disco

un disco abierto de radio\(δ\) centrado en el punto\((a,b)\)

\(δ\)bola

todos los puntos en\(\mathbb{R}^3\) mentir a una distancia de menos\(δ\) de\((x_0,y_0,z_0)\)

punto interior

un punto\(P_0\) de\(\mathbb{R}\) es un punto límite si hay un\(δ\) disco centrado alrededor\(P_0\) contenido completamente en\(\mathbb{R}\)

conjunto abierto

un conjunto\(S\) que no contiene ninguno de sus puntos de contorno

región

un subconjunto abierto, conectado y no vacío de\(\mathbb{R}^2\)