14.3: Derivadas parciales
- Page ID
- 116226
- Calcular las derivadas parciales de una función de dos variables.
- Calcular las derivadas parciales de una función de más de dos variables.
- Determinar las derivadas de orden superior de una función de dos variables.
- Explicar el significado de una ecuación diferencial parcial y dar un ejemplo.
Ahora que hemos examinado límites y continuidad de funciones de dos variables, podemos proceder a estudiar derivadas. Encontrar derivadas de funciones de dos variables es el concepto clave en este capítulo, con tantas aplicaciones en matemáticas, ciencias e ingeniería como diferenciación de funciones de una sola variable. Sin embargo, ya hemos visto que los límites y la continuidad de las funciones multivariables tienen nuevos problemas y requieren de nueva terminología e ideas para tratarlos. Esto también se traslada a la diferenciación.
Derivadas de una función de dos variables
Al estudiar derivadas de funciones de una variable, encontramos que una interpretación de la derivada es una tasa instantánea de cambio de\(y\) como una función de la notación\(x.\) Leibniz para la derivada es la\(dy/dx,\) que implica que\(y\) es la variable dependiente y\(x\) es la variable independiente. Para una función\(z=f(x,y)\) de dos variables,\(x\) y\(y\) son las variables independientes y\(z\) es la variable dependiente. Esto plantea dos preguntas de inmediato: ¿Cómo adaptamos la notación Leibniz para funciones de dos variables? Además, ¿qué es una interpretación de la derivada? La respuesta radica en las derivadas parciales.
Dejar\(f(x,y)\) ser una función de dos variables. Entonces la derivada parcial de\(f\) con respecto a\(x\), escrita como\(∂f/∂x,\), o\(f_x,\) se define como
\[\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1} \]
La derivada parcial de\(f\) con respecto a\(y\), escrita como\(∂f/∂y\), o\(f_y,\) se define como
\[\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2} \]
Esta definición ya muestra dos diferencias. Primero, la notación cambia, en el sentido de que todavía usamos una versión de la notación Leibniz, pero la\(d\) en la notación original se sustituye por el símbolo\(∂\). (Este redondeado\(“d”\) suele llamarse “parcial”, por lo que\(∂f/∂x\) se habla como el “parcial de\(f\) con respecto a”\(x\).) Este es el primer indicio de que estamos tratando con derivados parciales. Segundo, ahora tenemos dos derivadas diferentes que podemos tomar, ya que hay dos variables independientes diferentes. Dependiendo de la variable que elijamos, podemos llegar a diferentes derivadas parciales por completo, y muchas veces lo hacemos.
Usar la definición de la derivada parcial como límite para calcular\(∂f/∂x\) y\(∂f/∂y\) para la función
\[f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber \]
Solución
Primero, calcule\(f(x+h,y).\)
\[\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \nonumber \]
A continuación, sustituya esto en la Ecuación\ ref {pd1} y simplifique:
\ [\ begin {alinear*}\ dfrac {f} {x} &=\ lim_ {h→0}\ dfrac {f (x+h, y) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2+2xh+h^2−3xy−3hy+2^y2−4x−4h+5y−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12−x^2+3xy−2y^2+4x−4h+5y−12−x^2+3xy−2y^2+4x−4x−5y+12} {h}\\
&=\ lim_ {h→0}\ dfrac {2 xh+h^2−3hy−4h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (2x+h−3y−4)} {h}\\
&=\ lim_ {h→0} (2x+h−3y−4)\\
&=2x−3y−4. \ end {alinear*}\]
Para calcular\(\dfrac{∂f}{∂y}\), primero calcule\(f(x,y+h):\)
\[\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}\]
A continuación, sustituya esto en la Ecuación\ ref {pd2} y simplifique:
\ [\ begin {alinear*}\ dfrac {f} {y} &=\ lim_ {h→0}\ dfrac {f (x, y+h) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2−3xy−3xh+2y^2+4yh+2h^2h^2h^2h^2h^2h^2h^−4x+5y+5h−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2−3xy−3xh+2y^2+4yh+2h^2h^2−4x+5y+5h−12−x^2+3xy−y2h+2h^2h^2h^2−4x+5h−12−x^2+3xy−y2^2+4x−5y+12} {h}\\
&=\ lim_ {h→0}\ dfrac {−3xh+4yh+2h^2+5h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (−3x+4y+2h+5)} {h}\\
&=\ lim_ {h→0} (−3x+4y+2h+5)\\
&=−3x+4y+5\ end {aline*}\]
Usar la definición de la derivada parcial como límite para calcular\(∂f/∂x\) y\(∂f/∂y\) para la función
\[f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber \]
- Pista
-
Usa Ecuaciones\ ref {pd1} y\ ref {pd2} de la definición de derivadas parciales.
- Responder
-
\(\dfrac{∂f}{∂x}=8x+2y+3\)
\(\dfrac{∂f}{∂y}=2x−2y−2\)
La idea a tener en cuenta a la hora de calcular derivadas parciales es tratar todas las variables independientes, distintas de la variable con respecto a la que nos estamos diferenciando, como constantes. Después se procede a diferenciar como con una función de una sola variable. Para ver por qué esto es cierto, primero arregla\(y\) y define\(g(x)=f(x,y)\) como una función de\(x\). Entonces
\[\begin{align*} g′(x) &=\lim_{h→0}\dfrac{g(x+h)−g(x)}{h} \\[6pt] &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\[6pt] &=\dfrac{∂f}{∂x}. \end{align*}\]
Lo mismo es cierto para calcular la derivada parcial de\(f\) con respecto a\(y\). Esta vez, fijar\(x\) y definir\(h(y)=f(x,y)\) como una función de\(y\). Entonces
\[\begin{align*} h′(x) &=\lim_{k→0}\dfrac{h(x+k)−h(x)}{k} \\[6pt] &=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k} \\[6pt] &=\dfrac{∂f}{∂y}. \end{align*}\]
Se aplican todas las reglas de diferenciación.
Calcular\(∂f/∂x\) y\(∂f/∂y\) para las siguientes funciones manteniendo la variable opuesta constante y luego diferenciando:
- \(f(x,y)=x^2−3xy+2y^2−4x+5y−12\)
- \(g(x,y)=\sin(x^2y−2x+4)\)
Solución:
a. Para calcular\(∂f/∂x\), tratar la variable\(y\) como una constante. Luego, diferencie\(f(x,y)\) con respecto al\(x\) uso de las reglas de suma, diferencia y poder:
\[\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}\]
Las derivadas del tercer, quinto y sexto términos son todas cero porque no contienen la variable\(x\), por lo que se tratan como términos constantes. La derivada del segundo término es igual al coeficiente de\(x\), que es\(−3y\). Cálculo\(∂f/∂y\):
\[\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \nonumber \]
Estas son las mismas respuestas obtenidas en Ejemplo\(\PageIndex{1}\).
b. Para calcular\(∂g/∂x,\) tratar la variable y como una constante. Luego diferencie\(g(x,y)\) con respecto al\(x\) uso de la regla de cadena y la regla de poder:
\[\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}\]
Para calcular\(∂g/∂y,\) tratar la variable\(x\) como una constante. Luego diferencie\(g(x,y)\) con respecto al\(y\) uso de la regla de cadena y la regla de poder:
\[ \begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \nonumber \]
Calcular\(∂f/∂x\) y\(∂f/∂y\) para la función
\[f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber \]
manteniendo constante la variable opuesta, luego diferenciando.
- Pista
-
Usa Ecuaciones\ ref {pd1} y\ ref {pd1} de la definición de derivadas parciales.
- Responder
-
\(\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)\)
\(\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)\)
¿Cómo podemos interpretar estas derivadas parciales? Recordemos que la gráfica de una función de dos variables es una superficie en\(R^3\). Si eliminamos el límite de la definición de la derivada parcial con respecto a\(x\), el cociente de diferencia permanece:
\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]
Esto se asemeja al cociente de diferencia para la derivada de una función de una variable, excepto por la presencia de la\(y\) variable. La figura\(\PageIndex{1}\) ilustra una superficie descrita por una función arbitraria.\(z=f(x,y).\)
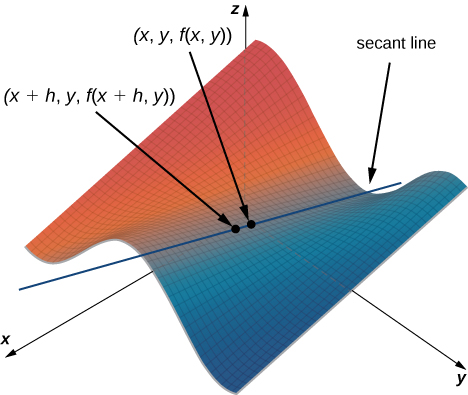
En la Figura\(\PageIndex{1}\), el valor de\(h\) es positivo. Si graficamos\(f(x,y)\) y\(f(x+h,y)\) para un punto arbitrario\((x,y),\) entonces la pendiente de la línea secante que pasa por estos dos puntos viene dada por
\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]
Esta línea es paralela al\(x\) eje -eje. Por lo tanto, la pendiente de la línea secante representa una tasa promedio de cambio de la función a\(f\) medida que viajamos paralelos al\(x\) eje -eje. A medida que\(h\) se acerca a cero, la pendiente de la línea secante se acerca a la pendiente de la línea tangente.
Si elegimos cambiar\(y\) en lugar de\(x\) por el mismo valor incremental\(h\), entonces la línea secante es paralela al\(y\) eje -y también lo es la línea tangente. Por lo tanto,\(∂f/∂x\) representa la pendiente de la línea tangente que pasa por el punto\((x,y,f(x,y))\) paralelo al\(x\) eje -y\(∂f/∂y\) representa la pendiente de la línea tangente que pasa por el punto\((x,y,f(x,y))\) paralelo al\(y\) eje -eje. Si queremos encontrar la pendiente de una línea tangente que pasa por el mismo punto en cualquier otra dirección, entonces necesitamos lo que se llama derivadas direccionales.
Ahora volvemos a la idea de los mapas de contorno, que introdujimos en Funciones de Varias Variables. Podemos usar un mapa de contorno para estimar derivadas parciales de una función\(g(x,y)\).
Usar un mapa de curvas de nivel para estimar\(∂g/∂x\) en el punto\((\sqrt{5},0)\) para la función
\[g(x,y)=\sqrt{9−x^2−y^2}. \nonumber \]
Solución
La figura\(\PageIndex{2}\) representa un mapa de contorno para la función\(g(x,y)\).
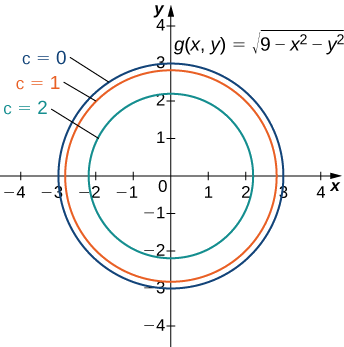
El círculo interno en el mapa de contorno corresponde\(c=2\) y el siguiente círculo hacia fuera corresponde a\(c=1\). El primer círculo viene dado por la ecuación\(2=\sqrt{9−x^2−y^2}\); el segundo círculo viene dado por la ecuación\(1=\sqrt{9−x^2−y^2}\). La primera ecuación simplifica a\(x^2+y^2=5\) y la segunda ecuación simplifica a\(x^2+y^2=8.\) La\(x\) -intercepción del primer círculo es\((\sqrt{5},0)\) y la\(x\) -intercepción del segundo círculo es\((2\sqrt{2},0)\). Podemos estimar el valor de\(∂g/∂x\) evaluado en el punto\((\sqrt{5},0)\) usando la fórmula de pendiente:
\[ \begin{align*} \left.\dfrac{∂g}{∂x}\right|_{(x,y) = (\sqrt{5},0)} &≈ \dfrac{g(\sqrt{5},0)−g(2\sqrt{2},0)}{\sqrt{5}−2\sqrt{2}} \\ &= \dfrac{2−1}{\sqrt{5}−2\sqrt{2}} \\ &=\dfrac{1}{\sqrt{5}−2\sqrt{2}} ≈−1.688. \end{align*}\]
Para calcular el valor exacto de\(∂g/∂x\) evaluado en el punto\((\sqrt{5},0)\), comenzamos por encontrar\(∂g/∂x\) usando la regla de la cadena. Primero, reescribimos la función como
\[g(x,y)=\sqrt{9−x^2−y^2}=(9−x^2−y^2)^{1/2} \nonumber \]
y luego diferenciar con respecto a\(x\) mientras se mantiene\(y\) constante:
\[ \begin{align*} \dfrac{∂g}{∂x} &=\dfrac{1}{2}(9−x^2−y^2)^{−1/2}(−2x) \\[4pt] &=−\dfrac{x}{\sqrt{9−x^2−y^2}}. \end{align*}\]
A continuación, evaluamos esta expresión usando\(x=\sqrt{5}\) y\(y=0\):
\ [\ begin {alinear*}\ dfrac {g} {x} _ {(x, y) = (\ sqrt {5} ,0)} &=−\ dfrac {\ sqrt {5}} {\ sqrt {9− (\ sqrt {5}) ^2− (0) ^2}}\\ [4pt]
&=\ dfrac\ sqrt {5}} {\ sqrt {4}}\\ [4pt]
&=−\ dfrac {\ sqrt {5}} {2} ≈−1.118. \ end {align*}\ nonumber\]
La estimación para la derivada parcial corresponde a la pendiente de la línea secante que pasa por los puntos\((\sqrt{5},0,g(\sqrt{5},0))\) y\((2\sqrt{2},0,g(2\sqrt{2},0))\). Representa una aproximación a la pendiente de la línea tangente a la superficie a través del punto\((\sqrt{5},0,g(\sqrt{5},0)),\) que es paralelo al\(x\) eje.
Usar un mapa de curvas de nivel para estimar\(∂f/∂y\) en el punto\((0,\sqrt{2})\) para la función
\[ f(x,y)=x^2−y^2.\nonumber \]
Compare esto con la respuesta exacta.
- Pista
-
Cree un mapa de curvas de nivel para\(f\) usar valores\(c\) de\(−3\) a\(3\). ¿Cuál de estas curvas pasa por el punto\((0,\sqrt{2})?\)
- Responder
-
Usando las curvas correspondientes\(c=−2\) y\(c=−3,\) obtenemos
\ [\ begin {align*}\ left. \ dfrac {f} {y}\ derecha|_ {(x, y) = (0,\ sqrt {2})} &≈\ dfrac {f (0,\ sqrt {3}) −f (0,\ sqrt {2})} {\ sqrt {3} −\ sqrt {2}}\\ [4pt]
&=\ dfrac {−3− (−2)} {\ sqrt {3} −\ sqrt {2}} ⋅\ dfrac {\ sqrt {3} +\ sqrt {2}} {\ sqrt {3} +\ sqrt {2}}\\ [4pt]
&=−\ sqrt {3} −\ sqrt {2} ≈−3.146. \ end {alinear*}\]La respuesta exacta es
\[ \left. \dfrac{∂f}{∂y} \right|_{(x,y)=(0,\sqrt{2})}=(−2y|_{(x,y)=(0,\sqrt{2})}=−2\sqrt{2}≈−2.828. \nonumber \]
Funciones de más de dos variables
Supongamos que tenemos una función de tres variables, tales como\(w=f(x,y,z).\) Podemos calcular derivadas parciales de\(w\) con respecto a cualquiera de las variables independientes, simplemente como extensiones de las definiciones para derivadas parciales de funciones de dos variables.
Dejar\(f(x,y,z)\) ser una función de tres variables. Entonces, la derivada parcial de\(f\) con respecto a\(x\), escrita como\(∂f/∂x,\) o\(f_x,\) se define como
\[\dfrac{∂f}{∂x}=f_x(x,y,z)=\lim_{h→0}\dfrac{f(x+h,y,z)−f(x,y,z)}{h}. \label{PD2a} \]
La derivada parcial de\(f\) con respecto a\(y\), escrita como\(∂f/∂y\), o\(f_y\), se define como
\[\dfrac{∂f}{∂y}=f_y(x,y,z)=\lim_{k→0}\dfrac{f(x,y+k,z)−f(x,y,z)}{k.} \label{PD2b} \]
La derivada parcial de\(f\) con respecto a\(z\), escrita como\(∂f/∂z\), o\(f_z\), se define como
\[\dfrac{∂f}{∂z}=f_z(x,y,z)=\lim_{m→0}\dfrac{f(x,y,z+m)−f(x,y,z)}{m}. \label{PD2c} \]
Podemos calcular una derivada parcial de una función de tres variables utilizando la misma idea que usamos para una función de dos variables. Por ejemplo, si tenemos una función\(f\) de\(x,y\), y\(z\), y queremos calcular\(∂f/∂x\), entonces tratamos las otras dos variables independientes como si fueran constantes, luego diferenciamos con respecto a\(x\).
Usar la definición límite de derivadas parciales para calcular\(∂f/∂x\) para la función
\[ f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z. \nonumber \]
Luego, encuentra\(∂f/∂y\) y\(∂f/∂z\) fijando las otras dos variables constantes y diferenciando en consecuencia.
Solución:
Primero calculamos\(∂f/∂x\) usando la Ecuación\ ref {PD2a}, luego calculamos las otras dos derivadas parciales manteniendo constantes las variables restantes. Para usar la ecuación para encontrar\(∂f/∂x\), primero necesitamos calcular\(f(x+h,y,z):\)
\ [\ begin {alinear*} f (x+h, y, z) &= (x+h) ^2−3 (x+h) y+2y^2−4 (x+h) z+5yz^2−12 (x+h) +4y−3z\\ [4pt]
&=x^2+2xh+h^2−3xy−3xh+2y^2−4xz−4hz+5yz^2−12x−12h+4y−3z\ end {alinear*}\ nonumber\]
y recordemos que\(f(x,y,z)=x^2−3xy+2y^2−4zx+5yz^2−12x+4y−3z.\) A continuación, sustituimos estas dos expresiones en la ecuación:
\ [\ begin {alinear*}\ dfrac {f} {x} &=\ lim_ {h→0}\ izquierda [\ dfrac {x^2+2xh+h^2−3xy-3hy+2y^2−4xz−4hz+5yz^2−12x−12h+4y−3zh−x^2−3xy+2y^^2y^3xy+2y^y^2y^3xy+2y^y^2y^xy+2y^2−4xz+5yz^2−12x+4y−3z} {h}\ derecha]\\ [4pt]
&=\ lim_ {h→0}\ izquierda [\ dfrac {2xh+h^2−3hy−4hz−12h} {h}\ derecha]\\ [4pt]
&=\ lim_ {h→0}\ izquierda [d\ frac {h (2x+h−3y−4z−12 )} {h}\ derecha]\\ [4pt]
&=\ lim_ {h→0} (2x+h−3y−4z−12)\\ [4pt]
&=2x−3y−4z−12. \ end {align*}\ nonumber\]
Entonces nos encontramos\(∂f/∂y\) sosteniendo\(x\) y\(z\) constante. Por lo tanto, cualquier término que no incluya la variable\(y\) es constante, y su derivada es cero. Podemos aplicar las reglas de suma, diferencia y potencia para funciones de una variable:
\ [\ begin {align*} &\ dfrac {} {y}\ izquierda [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z\ derecha]\\ [4pt]
&=\ dfrac {} {} {y} [x^2] −\ dfrac {} {y} [3xy] +\ dfrac {} {y} [2y^2] −\ dfrac {} {y} [4xz] +\ dfrac {} {y} [5yz^2] −\ dfrac {} {} {y} [12x] +\ dfrac {} {} [4y] −\ dfrac {} {z} [3z]\\ [4pt]
&=0−3x+4y−0+5z^2−0+4−0 \\ [4pt]
&=−3x+4y+5z^2+4. \ end {alinear*}\]
Para calcular\(∂f/∂z,\) mantenemos\(x\) y\(y\) constantes y aplicamos las reglas de suma, diferencia y potencia para funciones de una variable:
\ [\ begin {align*} &\ dfrac {} {z} [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z]\\ [4pt]
&=\ dfrac {} {z} [x^2] −\ dfrac {} {z} [3xy] +\ frac {} {z} [2y^2] −\ dfrac {} {z} [4xz] +\ dfrac {} {z} [5yz^2] −\ dfrac {} {z} [12x] +\ dfrac {} {z} [4y] −\ dfrac {} {z} [3z]\\ [4pt]
&=0−0+0−4x+10yz−0+0−3\\ [4pt]
&=−4x+10yz−3\ end {align*}\]
Usar la definición límite de derivadas parciales para calcular\(∂f/∂x\) para la función
\[f(x,y,z)=2x^2−4x^2y+2y^2+5xz^2−6x+3z−8.\nonumber \]
Luego encuentra\(∂f/∂y\) y\(∂f/∂z\) fijando las otras dos variables constantes y diferenciando en consecuencia.
- Pista
-
Utilice la estrategia en el ejemplo anterior.
- Responder
-
\(\dfrac{∂f}{∂x}=4x−8xy+5z^2−6,\dfrac{∂f}{∂y}=−4x^2+4y,\dfrac{∂f}{∂z}=10xz+3\)
Calcular las tres derivadas parciales de las siguientes funciones.
- \(f(x,y,z)=x^2y−4xz+y^2x−3yz\)
- \(g(x,y,z)=\sin(x^2y−z)+\cos(x^2−yz)\)
Solución
En cada caso, trata todas las variables como constantes excepto aquella cuya derivada parcial estás calculando.
a.
\ [\ begin {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ izquierda [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ derecha]\\ [6pt]
&=\ dfrac {\ dfrac {\ dfrac {} {x} (x^2y−4xz+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {x} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(2xy−4z) (x−3yz) − (x^2y−4xz+z+y^2) (1)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {2x^2y−6xy^2z−4xz+12yz^2−x^2y+4xz−y^2} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^2y−6xy^2z−4xz+12yz^2+4xz−y^2} {(x−3y^yz) ^2}\ end {alinear*}\]
\ [\ begin {align*}\ dfrac {f} {y} &=\ dfrac {} {y}\ izquierda [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ derecha]\\ [6pt]
&=\ dfrac {\ dfrac {\ dfrac {} {y} (x^2y−4xx z+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {y} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(x^2+2y) (x−3yz) − (x^2y−4xz+z+y^2) (−3z)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^3−3x^2yz+2xy−6y^2z+3x^2yz−12xz^2+3y^2z} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^3+2xy−3y^2z−12xz^2} {(^−3yz) 2}\ final {alinear*}\]
\ [\ begin {align*}\ dfrac {f} {z} &=\ dfrac {} {z}\ izquierda [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ derecha]\\ [6pt]
&=\ dfrac {\ dfrac {\ dfrac {} {z} (x^2y−4xz+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {z} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(−4x) (x−3yz) − (x^2y−4xz+y^2) (−3y)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {−4x^2+12xyz+3x^2y^2−12xyz+3y^3} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {−4x^2+3x^2y^2+3y^3} {(x−3yz) ^2}\ end {align*}\]
b.
\ [\ begin {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ izquierda [\ sin (x^2y−z) +\ cos (x^2−yz)\ derecha]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {x} (x^^2y−z) − (\ sin (x^2−yz))\ dfrac {} {x} (x^2−yz)\\ [6pt]
&=2xy\ cos (x^2y−z) −2x\ sin (x^2−yz)\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {y} &=\ dfrac {} {y} [\ sin (x^2y−z) +\ cos (x^2−yz)]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {y} (x^2y−z) − (\ sin (x^2−yz))\ dfrac {} {y} (x^2−yz)\\ [6pt]
&=x^2\ cos (x^2y−z) +z\ sin (x^2−yz)\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {z} &=\ dfrac {} {z} [\ sin (x^2y−z) +\ cos (x^2−yz)]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {z} (x^2y−z) − (\ sin (x^2−yz))\ dfrac {} {z} (x^2−yz)\\ [6pt]
&=−\ cos (x^2y−z) +y\ sin (x^2−yz)\ end {align*}\ nonumber\]
Calcular\(∂f/∂x, ∂f/∂y,\) y\(∂f/∂z\) para la función
\[f(x,y,z)=\sec(x^2y)−\tan(x^3yz^2). \nonumber \]
- Pista
-
Utilice la estrategia en el ejemplo anterior.
- Responder
-
\(\dfrac{∂f}{∂x}=2xy\sec(x^2y)\tan(x^2y)−3x^2yz^2\sec^2(x^3yz^2)\)
\(\dfrac{∂f}{∂y}=x^2\sec(x^2y)\tan(x^2y)−x^3z^2\sec^2(x^3yz^2)\)
\(\dfrac{∂f}{∂z}=−2x^3yz\sec^2(x^3yz^2)\)
Derivadas parciales de orden superior
Considere la función
\[f(x,y)=2x^3−4xy^2+5y^3−6xy+5x−4y+12. \nonumber \]
Sus derivados parciales son
\[\dfrac{∂f}{∂x}=6x^2−4y^2−6y+5 \nonumber \]
y
\[\dfrac{∂f}{∂y}=−8xy+15y^2−6x−4. \nonumber \]
Cada una de estas derivadas parciales es una función de dos variables, por lo que podemos calcular derivadas parciales de estas funciones. Al igual que con las derivadas de funciones de una sola variable, podemos llamar a estas derivadas de segundo orden, derivadas de tercer orden, y así sucesivamente. En general, se les conoce como derivados parciales de orden superior. Hay cuatro derivadas parciales de segundo orden para cualquier función (siempre que existan todas):
\ [\ begin {align*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ left [\ dfrac {f} {x}\ derecha]\\ [4pt]
\ dfrac {^2f} {yx} &=\ dfrac {} {}\ left [\ dfrac {f} {x}\ derecha]\\ [4pt]
\ dfrac {^2f} {x} &=\ dfrac {} {x}\ izquierda [\ dfrac {f} {y}\ derecha]\\ [4pt]
\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ izquierda [\ dfrac {f} {y}\ derecha]. \ end {alinear*}\]
Una notación alternativa para cada uno es\(f_{xx},f_{xy},f_{yx},\) y\(f_{yy}\), respectivamente. Las derivadas parciales de orden superior calculadas con respecto a diferentes variables, tales como\(f_{xy}\) y\(f_{yx}\), se denominan comúnmente derivadas parciales mixtas.
Calcular las derivadas parciales de cuatro segundos para la función
\[f(x,y)=xe^{−3y}+\sin(2x−5y).\label{Ex6e1} \]
Solución:
Para calcular\(\dfrac{∂^2f}{∂x^2}\) y\(\dfrac{∂^2f}{∂y∂x}\), primero calculamos\(∂f/∂x\):
\[\dfrac{∂f}{∂x}=e^{−3y}+2\cos(2x−5y). \label{Ex6e2} \]
Para calcular\(\dfrac{∂^2f}{∂x^2}\), diferenciar\(∂f/∂x\) (Ecuación\ ref {ex6e2}) con respecto a\(x\):
\ [\ begin {align*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ left [\ dfrac {f} {x}\ derecha]\\ [6pt]
&=\ dfrac {} {x} [e^ {−3y} +2\ cos (2x−5y)]\ [6pt]
&=−4\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂y∂x}\), diferenciar\(∂f/∂x\) (Ecuación\ ref {ex6e2}) con respecto a\(y\):
\ [\ begin {align*}\ dfrac {^2f} {y\, x} &=\ dfrac {} {y}\ izquierda [\ dfrac {f} {x}\ derecha]\\ [6pt]
&=\ dfrac {} {} {y} [e^ {−3y} +2\ cos (2x−5y)]\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂x∂y}\) y\(\dfrac{∂^2f}{∂y^2}\), primero calcular\(∂f/∂y\):
\[\dfrac{∂f}{∂y}=−3xe^{−3y}−5\cos(2x−5y). \label{Ex6e5} \]
Para calcular\(\dfrac{∂^2f}{∂x∂y}\), diferenciar\(∂f/∂y\) (Ecuación\ ref {ex6e5}) con respecto a\(x\):
\ [\ begin {align*}\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ izquierda [\ dfrac {f} {y}\ derecha]\\ [6pt]
&=\ dfrac {} {x} [−3xe^ {−3y} −5\ cos (2x−5y)]\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂y^2}\), diferenciar\(∂f/∂y\) (Ecuación\ ref {ex6e5}) con respecto a\(y\):
\ [\ begin {align*}\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ izquierda [\ dfrac {f} {y}\ derecha]\\ [6pt]
&=\ dfrac {} {} {y} [−3xe^ {−3y} −5\ cos (2x−5y)]\\ [6pt]
&=9xe^ {−3y} −25\ sin (2x−5y). \ end {align*}\ nonumber\]
Calcular las derivadas parciales de cuatro segundos para la función
\[f(x,y)=\sin(3x−2y)+\cos(x+4y).\nonumber \]
- Pista
-
Sigue los mismos pasos que en el ejemplo anterior.
- Responder
-
\(\dfrac{∂^2f}{∂x^2}=−9\sin(3x−2y)−\cos(x+4y)\)
\(\dfrac{∂^2f}{∂y∂x}=6\sin(3x−2y)−4\cos(x+4y)\)
\(\dfrac{∂^2f}{∂x∂y}=6\sin(3x−2y)−4\cos(x+4y)\)
\(\dfrac{∂^2f}{∂y^2}=−4\sin(3x−2y)−16\cos(x+4y)\)
En este punto habría que notar que, tanto en Ejemplo\(\PageIndex{6}\) como en el punto de control, era cierto que\(\dfrac{∂^2f}{∂y∂x}=\dfrac{∂^2f}{∂x∂y}\). Bajo ciertas condiciones, esto siempre es cierto. De hecho, es consecuencia directa del siguiente teorema.
Supongamos que\(f(x,y)\) se define en un disco abierto\(D\) que contiene el punto\((a,b)\). Si las funciones\(f_{xy}\) y\(f_{yx}\) son continuas encendidas\(D\), entonces\(f_{xy}=f_{yx}\).
El teorema de Clairaut garantiza que mientras las derivadas mixtas de segundo orden sean continuas, el orden en que elegimos diferenciar las funciones (es decir, qué variable va primero, luego segundo, y así sucesivamente) no importa. También se puede extender a derivados de orden superior. La prueba del teorema de Clairaut se puede encontrar en la mayoría de los libros de cálculo avanzados.
Se pueden calcular otras dos derivadas parciales de segundo orden para cualquier función\(f(x,y).\) La derivada parcial\(f_{xx}\) es igual a la derivada parcial de\(f_x\) con respecto a\(x\), y\(f_{yy}\) es igual a la derivada parcial de\(f_y\) con respecto a\(y\).
Ecuaciones diferenciales parciales
Anteriormente, estudiamos ecuaciones diferenciales en las que la función desconocida tenía una variable independiente. Una ecuación diferencial parcial es una ecuación que involucra una función desconocida de más de una variable independiente y una o más de sus derivadas parciales. Ejemplos de ecuaciones diferenciales parciales son
\[\underset{\text{heat equation in two dimensions}}{u_t=c^2(u_{xx}+u_{yy})} \nonumber \]
\[\underset{\text{wave equation in two dimensions}}{u_{tt}=c^2(u_{xx}+u_{yy})} \nonumber \]
\[\underset{\text{Laplace’s equation in two dimensions}} {u_{xx}+u_{yy}=0} \nonumber \]
En las ecuaciones de calor y onda, la función desconocida\(u\) tiene tres variables independientes:\(t\),\(x\), y\(y\) con\(c\) es una constante arbitraria. Las variables independientes\(x\) y\(y\) se consideran variables espaciales, y la variable\(t\) representa el tiempo. En la ecuación de Laplace, la función desconocida\(u\) tiene dos variables independientes\(x\) y\(y\).
Verificar que
\[u(x,y,t)=5\sin(3πx)\sin(4πy)\cos(10πt) \nonumber \]
es una solución a la ecuación de onda
\[u_{tt}=4(u_{xx}+u_{yy}). \label{Ex7Eq2} \]
Solución
Primero, calculamos\(u_{tt},u_{xx},\) y\(u_{yy}:\)
\ [\ begin {align*} u_ {tt} (x, y, t) &=\ dfrac {} {t}\ izquierda [\ dfrac {u} {t}\ derecha]\\ [6pt]
&=\ dfrac {} {t} [5\ sin (3πx)\ sin (4πy) (−10π\ sin (πt))]\\ [6pt]
&=\ dfrac {} {t}\ izquierda [−50π\ sin (3πx)\ sin (4πy)\ sin (10πt)\ derecha]\\ [6pt]
&=−500π^2\ sin (3πx)\ sin (4πy)\ cos (10πt)\ final {alinear*}\]
\ [\ begin {align*} u_ {xx} (x, y, t) &=\ dfrac {} {x}\ izquierda [\ dfrac {u} {x}\ derecha]\\ [6pt]
&=\ dfrac {} {x}\ izquierda [15π\ cos (3πx)\ sin (4πy)\ cos (10πx t)\ derecha]\\ [6pt]
&=−45π^2\ sin (3πx)\ sin (4πy)\ cos (10πt)\ end {align*}\]
\ [\ begin {align*} u_ {yy} (x, y, t) &=\ dfrac {} {y}\ izquierda [\ dfrac {u} {y}\ derecha]\\ [6pt]
&=\ dfrac {} {}\ left [5\ sin (3πx) (4π\ cos (4πy))\ cos (10πt)\ derecha]\\ [6pt]
&=\ dfrac {} {y}\ izquierda [20π\ sin (3πx)\ cos (4πy)\ cos (10πt)\ derecha]\\ [6pt]
&=−80π^2\ sin (3πx)\ sin (4πy)\ cos ( 10πt). \ end {align*}\ nonumber\]
A continuación, sustituimos cada uno de estos en el lado derecho de la Ecuación\ ref {Ex7Eq2} y simplificamos:
\ [\ begin {alinear*} 4 (u_ {xx} +u_ {yy}) &=4 (−45π^2\ sin (3πx)\ sin (4πy)\ cos (10πt) +−80π^2\ sin (3πx)\ sin (4πy)\ cos (10πt))\\ [6pt]
&=4 (−125^π2\ sin (3πx)\ sin (4πy)\ cos (10πt))\\ [6pt]
&=−500π^2\ sin (3πx)\ sin (4πy)\ cos (10πt)\\ [6pt]
&=u_ {tt}. \ end {alinear*}\]
Esto verifica la solución.
Verificar que
\[u(x,y,t)=2\sin \left(\dfrac{x}{3} \right)\sin\left(\dfrac{y}{4} \right)e^{−25t/16} \nonumber \]
es una solución a la ecuación del calor
\[u_t=9(u_{xx}+u_{yy}). \nonumber \]
- Pista
-
Calcular las derivadas parciales y sustituirlas en el lado derecho.
- Responder
-
TBA
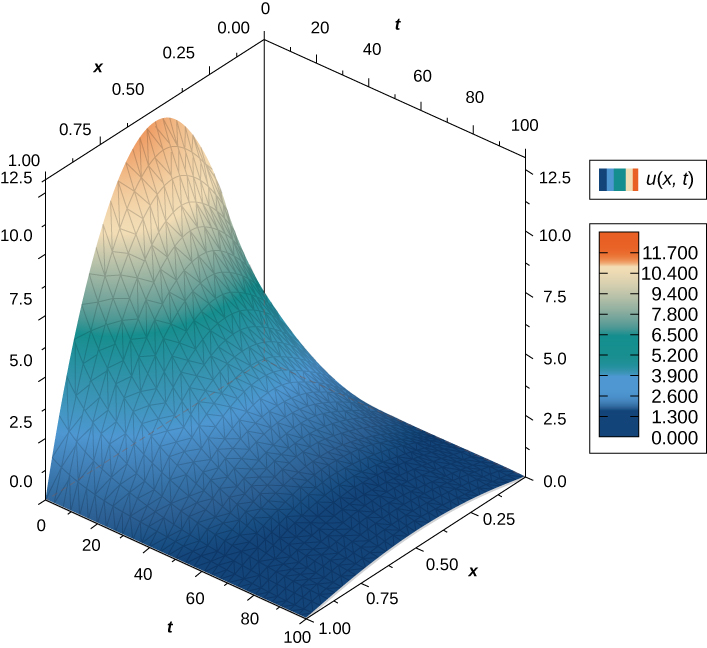
Dado que la solución a la ecuación bidimensional del calor es una función de tres variables, no es fácil crear una representación visual de la solución. Podemos graficar la solución para valores fijos de los\(t,\) cuales equivale a instantáneas de las distribuciones de calor en tiempos fijos. Estas instantáneas muestran cómo el calor se distribuye sobre una superficie bidimensional a medida que avanza el tiempo. La gráfica de la solución anterior en el momento\(t=0\) aparece en la Figura\(\PageIndex{3}\). A medida que avanza el tiempo, los extremos se nivelan, acercándose a cero cuando se\(t\) acerca al infinito.
Si consideramos la ecuación del calor en una dimensión, entonces es posible graficar la solución a lo largo del tiempo. La ecuación de calor en una dimensión se convierte
\[u_t=c^2u_{xx}, \nonumber \]
donde\(c^2\) representa la difusividad térmica del material en cuestión. Una solución de esta ecuación diferencial se puede escribir en la forma
\[u_m(x,t)=e^{−π^2m^2c^2t}\sin(mπx) \nonumber \]
donde\(m\) es cualquier entero positivo. Un gráfico de esta solución usando\(m=1\) aparece en la Figura\(\PageIndex{4}\), donde la distribución de temperatura inicial sobre un cable de longitud\(1\) viene dada por\(u(x,0)=\sin πx.\) Aviso que a medida que avanza el tiempo, el alambre se enfría. Esto se ve porque, de izquierda a derecha, la temperatura más alta (que ocurre en el medio del cable) disminuye y cambia de color de rojo a azul.
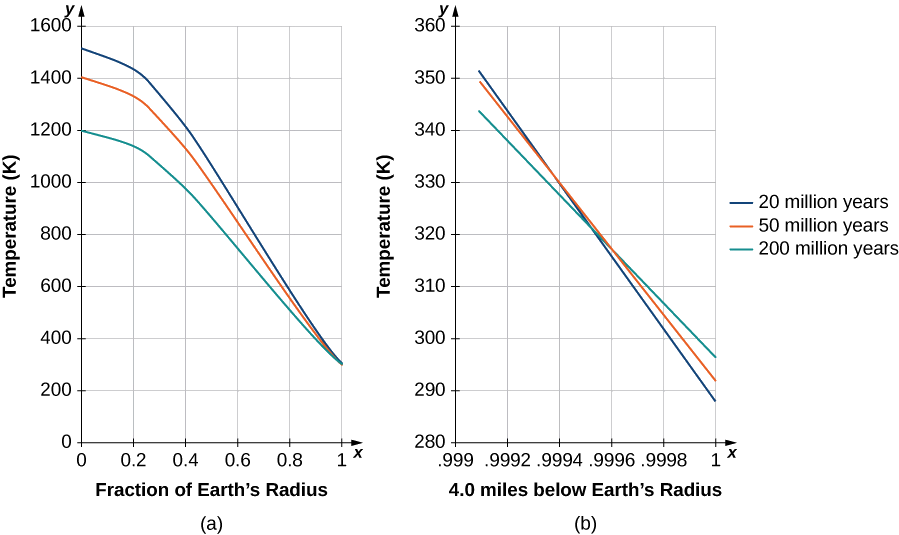
A finales del siglo XIX, los científicos del nuevo campo de la geología llegaban a la conclusión de que la Tierra debía tener “millones y millones” de años. Casi al mismo tiempo, Charles Darwin había publicado su tratado sobre la evolución. La opinión de Darwin era que la evolución necesitaba muchos millones de años para tener lugar, e hizo una audaz afirmación de que los campos de tiza de Weald, donde se encontraron fósiles importantes, eran el resultado de\(300\) millones de años de erosión.
En ese momento, el eminente físico William Thomson (Lord Kelvin) utilizó una importante ecuación diferencial parcial, conocida como la ecuación de difusión de calor, para estimar la edad de la Tierra determinando cuánto tiempo tardaría la Tierra en enfriarse de roca fundida a lo que teníamos en ese momento. Su conclusión fue un rango de 20 a 400 millones de años, pero muy probablemente alrededor de 50 millones de años. Durante muchas décadas, las proclamaciones de este ícono irrefutable de la ciencia no sentaron bien a los geólogos ni a Darwin.
Kelvin hizo suposiciones razonables basadas en lo que se conocía en su época, pero también hizo varias suposiciones que resultaron estar equivocadas. Una suposición incorrecta fue que la Tierra es sólida y que, por lo tanto, el enfriamiento era solo por conducción, justificando así el uso de la ecuación de difusión. Pero el error más grave fue perdonable —omisión del hecho de que la Tierra contiene elementos radiactivos que continuamente suministran calor bajo el manto de la Tierra. El descubrimiento de la radiactividad llegó cerca del final de la vida de Kelvin y reconoció que su cálculo tendría que ser modificado.
Kelvin utilizó el modelo simple unidimensional aplicado solo a la capa exterior de la Tierra, y derivó la edad de los gráficos y el gradiente de temperatura aproximadamente conocido cerca de la superficie de la Tierra. Echemos un vistazo a una versión más apropiada de la ecuación de difusión en coordenadas radiales, que tiene la forma
\[\dfrac{∂T}{∂t}=K\left[\dfrac{∂^2T}{∂^2r}+\dfrac{2}{r}\dfrac{∂T}{∂r}\right] \label{kelvin1} \].
Aquí,\(T(r,t)\) es la temperatura en función de\(r\) (medida desde el centro de la Tierra) y el tiempo\(t. K\) es la conductividad térmica, para la roca fundida, en este caso. El método estándar para resolver tal ecuación diferencial parcial es por separación de variables, donde expresamos la solución como el producto de funciones que contienen cada variable por separado. En este caso, escribiríamos la temperatura como
\[T(r,t)=R(r)f(t). \nonumber \]
- Sustituir esta forma en Ecuación\ ref {kelvin1} y, señalando que\(f(t)\) es constante con respecto a la distancia\((r)\) y\(R(r)\) es constante con respecto al tiempo\((t)\), mostrar que\[\dfrac{1}{f}\dfrac{∂f}{∂t}=\dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]. \nonumber \]
- Esta ecuación representa la separación de las variables que queremos. El lado izquierdo es solo una función de\(t\) y el lado derecho es solo una función de\(r\), y deben ser iguales para todos los valores de\(r\) y\(t\). Por lo tanto, ambos deben ser iguales a una constante. Llamemos a eso constante\(−λ^2\). (La conveniencia de esta elección se ve en la sustitución.) Entonces, tenemos\[\dfrac{1}{f}\dfrac{∂f}{∂t}=−λ^2 \text{and} \dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]=−λ^2. \nonumber \]
- Ahora, podemos verificar a través de la sustitución directa para cada ecuación que las soluciones son\(f(t)=Ae^{−λ^2t}\) y\(R(r)=B\left(\dfrac{\sin αr}{r}\right)+C\left(\dfrac{\cos αr}{r}\right)\), dónde\(α=λ/\sqrt{K}\). Tenga en cuenta que también\(f(t)=Ae^{+λn^2t}\) es una solución válida, por lo que podríamos haber elegido\(+λ^2\) para nuestra constante. ¿Ves por qué no sería válido para este caso a medida que aumenta el tiempo?
- Ahora apliquemos condiciones de contorno.
- La temperatura debe ser finita en el centro de la Tierra,\(r=0\). ¿Cuál de las dos constantes,\(B\) o\(C\), debe ser por lo tanto cero para mantenerse\(R\) finito\(r=0\)? (Recordemos que\(\sin(αr)/r→α=\) como\(r→0\), pero\(\cos(αr)/r\) se comporta de manera muy diferente.)
- Kelvin argumentó que cuando el magma llega a la superficie de la Tierra, se enfría muy rápidamente. Una persona a menudo puede tocar la superficie a las pocas semanas del flujo. Por lo tanto, la superficie alcanzó una temperatura moderada muy temprano y permaneció casi constante a una temperatura superficial\(T_s\). Por simplicidad, fijémonos\(T=0\) en\(r=R_E\) y encontremos α tal que esta sea la temperatura ahí para siempre\(t\). (Kelvin tomó el valor para ser\(300K≈80°F\). Podemos agregar esta\(300K\) constante a nuestra solución más adelante.) Para que esto sea cierto, el argumento sine debe ser cero at\(r=R_E\). Tenga en cuenta que α tiene una serie infinita de valores que satisface esta condición. Cada valor de\(α\) representa una solución válida (cada uno con su propio valor para\(A\)). La solución total o general es la suma de todas estas soluciones.
- Al\(t=0,\) suponer que toda la Tierra estaba a una temperatura inicial de calor\(T_0\) (Kelvin tomó esto para ser sobre\(7000K\).) La aplicación de esta condición límite implica la aplicación más avanzada de coeficientes de Fourier. Como se señala en la parte b. cada valor de\(α_n\) representa una solución válida, y la solución general es una suma de todas estas soluciones. Esto da como resultado una solución en serie:\[T(r,t)=\left(\dfrac{T_0R_E}{π}\right)\sum_n\dfrac{(−1)^{n−1}}{n}e^{−λn^2t}\dfrac{\sin(α_nr)}{r} \nonumber \] dónde\(\; α_n=nπ/R_E\).
Observe cómo los valores de\(α_n\) provienen de la condición de límite aplicada en la parte b. El término\(\dfrac{−1^{n−1}}{n}\) es la constante\(A_n\) para cada término de la serie, determinada a partir de la aplicación del método de Fourier. Dejando\(β=\dfrac{π}{R_E}\), examinar los primeros términos de esta solución que se muestran aquí y anotar cómo\(λ^2\) en lo exponencial hace que los términos superiores disminuyan rápidamente a medida que avanza el tiempo:
\[T(r,t)=\dfrac{T_0R_E}{πr}\left(e^{−Kβ^2t}(\sinβr)−\dfrac{1}{2}e^{−4Kβ^2t}(\sin2βr)+\dfrac{1}{3}e^{−9Kβ^2t}(\sin3βr)−\dfrac{1}{4}e^{−16Kβ^2t}(\sin4βr)+\dfrac{1}{5}e^{−25Kβ^2t}(\sin5βr)...\right). \nonumber \]
Cerca del tiempo se necesitan\(t=0,\) muchos términos de la solución para la precisión. Insertando valores para la conductividad\(K\) y\(β=π/R_E\) por tiempo que se aproximan a miles de años, solo los primeros términos hacen una contribución significativa. Kelvin solo necesitaba mirar la solución cerca de la superficie de la Tierra (Figura\(\PageIndex{6}\)) y, después de mucho tiempo, determinar a qué hora produjo mejor el gradiente de temperatura estimado conocido durante su época (\(1°F\)incremento per\(50ft\)). Simplemente eligió un rango de tiempos con un gradiente cercano a este valor. En la Figura\(\PageIndex{6}\), las soluciones se trazan y escalan, con la temperatura\(300−K\) superficial añadida. Tenga en cuenta que el centro de la Tierra sería relativamente frío. En su momento, se pensó que la Tierra debía ser sólida.
Epilog
El 20 de mayo de 1904, el físico Ernest Rutherford habló en la Royal Institution para anunciar un cálculo revisado que incluía la contribución de la radiactividad como fuente de calor de la Tierra. En palabras propias de Rutherford:
“Entré en la habitación, que estaba medio oscura, y actualmente vi a Lord Kelvin en la audiencia, y me di cuenta de que estaba metido en problemas en la última parte de mi discurso sobre la edad de la Tierra, donde mis puntos de vista entraban en conflicto con los suyos. Para mi alivio, Kelvin se quedó profundamente dormido, pero a medida que llegué al punto importante, vi al viejo pájaro sentarse, abrir un ojo y verle una mirada maléfica hacia mí.
Entonces vino una repentina inspiración, y dije que Lord Kelvin había limitado la edad de la Tierra, siempre que no se descubriera una nueva fuente [de calor]. Esa afirmación profética se refería a lo que ahora estamos considerando esta noche, ¡radio! ¡Contemplad! El viejo sonó sobre mí”.
Rutherford calculó una edad para la Tierra de unos 500 millones de años. El valor aceptado de hoy de la edad de la Tierra es de unos 4.6 mil millones de años.
Conceptos clave
- Una derivada parcial es una derivada que implica una función de más de una variable independiente.
- Para calcular una derivada parcial con respecto a una variable dada, tratar todas las demás variables como constantes y utilizar las reglas de diferenciación habituales.
- Las derivadas parciales de orden superior se pueden calcular de la misma manera que las derivadas de orden superior.
Ecuaciones Clave
Derivada parcial de\(f\) con respecto a\(x\)\[\dfrac{∂f}{∂x}=\displaystyle{\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h}} \nonumber \]
Derivada parcial de\(f\) con respecto a\(y\)\[\dfrac{∂f}{∂y}=\displaystyle{\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}} \nonumber \]
Glosario
- Derivadas parciales de orden superior
- derivados parciales de segundo orden o superiores, independientemente de que sean derivados parciales mixtos
- Derivados parciales mixtos
- derivadas parciales de segundo orden o superiores, en las que al menos dos de las diferenciaciones son con respecto a diferentes variables
- derivado parcial
- una derivada de una función de más de una variable independiente en la que todas las variables menos una se mantienen constantes
- ecuación diferencial parcial
- una ecuación que implica una función desconocida de más de una variable independiente y una o más de sus derivadas parciales