14.7: Problemas máximos/mínimos

Objetivos de aprendizaje

• Utilice derivadas parciales para localizar puntos críticos para una función de dos variables.
• Aplicar una segunda prueba derivada para identificar un punto crítico como máximo local, mínimo local o punto de sillín para una función de dos variables.
• Examine los puntos críticos y los puntos límite para encontrar valores máximos y mínimos absolutos para una función de dos variables.

Una de las aplicaciones más útiles para las derivadas de una función de una variable es la determinación de valores máximos y/o mínimos. Esta aplicación también es importante para funciones de dos o más variables, pero como hemos visto en secciones anteriores de este capítulo, la introducción de variables más independientes conduce a más resultados posibles para los cálculos. Las ideas principales de encontrar puntos críticos y usar pruebas derivadas siguen siendo válidas, pero aparecen nuevas arrugas al evaluar los resultados.

Puntos Críticos

Para las funciones de una sola variable, definimos puntos críticos como los valores de la variable en la que la derivada de la función es igual a cero o no existe. Para funciones de dos o más variables, el concepto es esencialmente el mismo, salvo por el hecho de que ahora estamos trabajando con derivadas parciales.

Definición: Puntos críticos

Dejar\(z=f(x,y)\) ser una función de dos variables que es diferenciable en un conjunto abierto que contiene el punto\((x_0,y_0)\). El punto\((x_0,y_0)\) se denomina punto crítico de una función de dos variables\(f\) si se mantiene una de las dos siguientes condiciones:

1. \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)
2. O bien\(f_x(x_0,y_0) \; \text{or} \; f_y(x_0,y_0)\) no existe.

Ejemplo\(\PageIndex{1}\): Finding Critical Points

Encuentra los puntos críticos de cada una de las siguientes funciones:

1. \(f(x,y)=\sqrt{4y^2−9x^2+24y+36x+36}\)
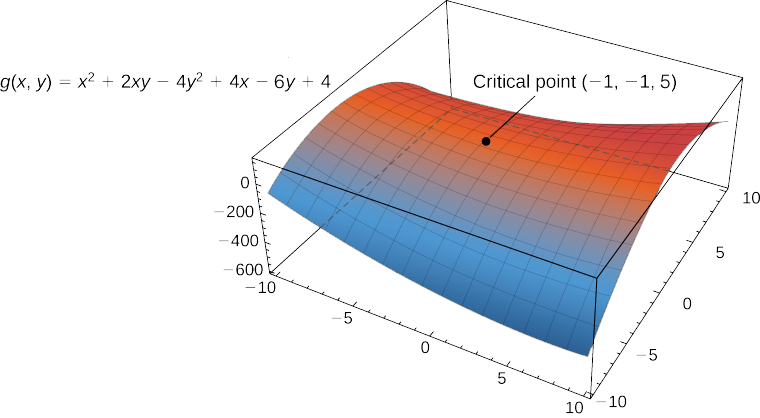
2. \(g(x,y)=x^2+2xy−4y^2+4x−6y+4\)

Solución

a. Primero, calculamos\(f_x(x,y) \; \text{and} \; f_y(x,y):\)

\[\begin{align*} f_x(x,y) &=\dfrac{1}{2}(−18x+36)(4y^2−9x^2+24y+36x+36)^{−1/2} \\[4pt] &=\dfrac{−9x+18}{\sqrt{4y^2−9x^2+24y+36x+36}} \end{align*}\]

\[\begin{align*} f_y(x,y) &=\dfrac{1}{2}(8y+24)(4y^2−9x^2+24y+36x+36)^{−1/2} \\[4pt] &=\dfrac{4y+12}{\sqrt{4y^2−9x^2+24y+36x+36}} \end{align*}. \nonumber \]

A continuación, establecemos cada una de estas expresiones igual a cero:

\[\begin{align*} \dfrac{−9x+18}{\sqrt{4y^2−9x^2+24y+36x+36}} &=0 \\[4pt] \dfrac{4y+12}{\sqrt{4y^2−9x^2+24y+36x+36}} &=0. \end{align*}\]

Luego, multiplica cada ecuación por su denominador común:

\[\begin{align*} −9x+18 &=0 \\[4pt] 4y+12 &=0. \end{align*}\]

Por lo tanto,\(x=2\) y\(y=−3,\) así\((2,−3)\) es un punto crítico de\(f\).

También debemos verificar la posibilidad de que el denominador de cada derivada parcial pueda ser igual a cero, provocando así que la derivada parcial no exista. Como el denominador es el mismo en cada derivada parcial, solo necesitamos hacer esto una vez:

\[4y^2−9x^2+24y+36x+36=0. \label{critical1} \]

La ecuación\ ref {critical1} representa una hipérbola. También hay que señalar que el dominio de\(f\) consiste en puntos que satisfacen la desigualdad

\[4y^2−9x^2+24y+36x+36≥0. \nonumber \]

Por lo tanto, cualquier punto en la hipérbola no solo son puntos críticos, también están en el límite del dominio. Para poner la hipérbola en forma estándar, utilizamos el método de completar el cuadrado:

\[\begin{align*} 4y^2−9x^2+24y+36x+36 &=0 \\[4pt] 4y^2−9x^2+24y+36x &=−36 \\[4pt] 4y^2+24y−9x^2+36x &=−36 \\[4pt] 4(y^2+6y)−9(x^2−4x) &=−36 \\[4pt] 4(y^2+6y+9)−9(x^2−4x+4) &=−36−36+36 \\[4pt] 4(y+3)^2−9(x−2)^2 &=−36.\end{align*}\]

Dividiendo ambos lados por\(−36\) pone la ecuación en forma estándar:

\[\begin{align*} \dfrac{4(y+3)^2}{−36}−\dfrac{9(x−2)^2}{−36} &=1 \\[4pt] \dfrac{(x−2)^2}{4}−\dfrac{(y+3)^2}{9} &=1. \end{align*}\]

Observe que ese punto\((2,−3)\) es el centro de la hipérbola.

Así, los puntos críticos de la función\(f\) son\( (2, -3) \) y todos los puntos sobre la hipérbola,\(\dfrac{(x−2)^2}{4}−\dfrac{(y+3)^2}{9}=1\).

b. Primero, calculamos\(g_x(x,y)\) y\(g_y(x,y)\):

\[\begin{align*} g_x(x,y) &=2x+2y+4 \\[4pt] g_y(x,y) &=2x−8y−6. \end{align*}\]

A continuación, establecemos cada una de estas expresiones igual a cero, lo que da un sistema de ecuaciones en\(x\) y\(y\):

\[\begin{align*} 2x+2y+4 &=0 \\[4pt] 2x−8y−6 &=0. \end{align*}\]

Restar la segunda ecuación de la primera da\(10y+10=0\), entonces\(y=−1\). Sustituir esto en la primera ecuación da\(2x+2(−1)+4=0\), entonces\(x=−1\).

Por lo tanto\((−1,−1)\) es un punto crítico de\(g\). No hay puntos en\(\mathbb{R}^2\) que hagan que no exista ninguna derivada parcial.

La figura\(\PageIndex{1}\) muestra el comportamiento de la superficie en el punto crítico.

Figura\(\PageIndex{1}\): La función\(g(x,y)\) tiene un punto crítico en\((−1,−1,5)\).

Ejercicio\(\PageIndex{1}\)

Encuentra el punto crítico de la función\(f(x,y)=x^3+2xy−2x−4y.\)

Pista

Calcular\(f_x(x,y)\) y\(f_y(x,y)\), luego establecerlos iguales a cero.

Contestar

El único punto crítico de\(f\) es\((2,−5)\).

El propósito principal para determinar los puntos críticos es ubicar máximos y mínimos relativos, como en el cálculo de una sola variable. Cuando se trabaja con una función de una variable, la definición de un extremo local implica encontrar un intervalo alrededor del punto crítico tal que el valor de la función sea mayor o menor que todos los demás valores de función en ese intervalo. Cuando se trabaja con una función de dos o más variables, trabajamos con un disco abierto alrededor del punto.

Definición: Extrema Global y Local

Dejar\(z=f(x,y)\) ser una función de dos variables que se define y continua en un conjunto abierto que contiene el punto\((x_0,y_0).\) Entonces\(f\) tiene un máximo local en\((x_0,y_0)\) si

\[f(x_0,y_0)≥f(x,y) \nonumber \]

para todos los puntos\((x,y)\) dentro de algún disco centrado en\((x_0,y_0)\). El número\(f(x_0,y_0)\) se denomina valor máximo local. Si la desigualdad precedente se mantiene para cada punto\((x,y)\) en el dominio de\(f\), entonces\(f\) tiene un máximo global (también llamado máximo absoluto) en\((x_0,y_0).\)

La función\(f\) tiene un mínimo local en\((x_0,y_0)\) si

\[f(x_0,y_0)≤f(x,y) \nonumber \]

para todos los puntos\((x,y)\) dentro de algún disco centrado en\((x_0,y_0)\). El número\(f(x_0,y_0)\) se denomina valor mínimo local. Si la desigualdad precedente se mantiene para cada punto\((x,y)\) en el dominio de\(f\), entonces\(f\) tiene un mínimo global (también llamado mínimo absoluto) en\((x_0,y_0)\).

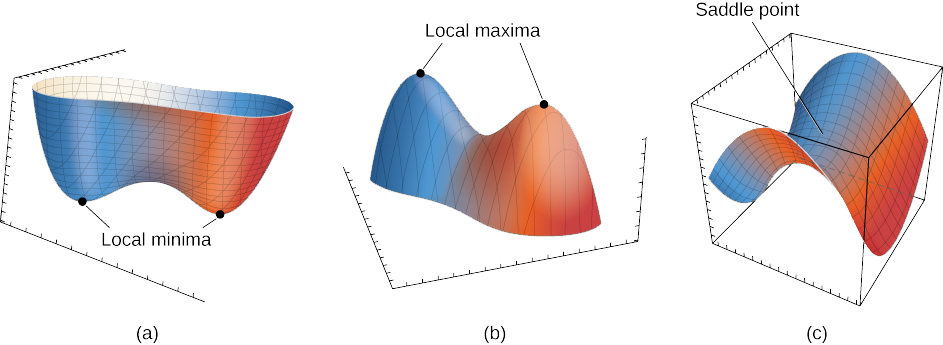
Si\(f(x_0,y_0)\) es un valor máximo local o mínimo local, entonces se denomina extremo local (ver la siguiente figura).

Figura\(\PageIndex{2}\): La gráfica de\(z=\sqrt{16−x^2−y^2}\) tiene un valor máximo cuando\((x,y)=(0,0)\). Logra su valor mínimo en el límite de su dominio, que es el círculo\(x^2+y^2=16.\)

En el Cálculo 1, mostramos que los extremos de funciones de una variable ocurren en puntos críticos. Lo mismo es cierto para las funciones de más de una variable, como se afirma en el siguiente teorema.

Teorema de Fermat para funciones de dos variables

Dejar\(z=f(x,y)\) ser una función de dos variables que se define y continua en un conjunto abierto que contiene el punto\((x_0,y_0)\). Supongamos\(f_x\) y\(f_y\) cada uno existe en\((x_0,y_0)\). Si f tiene un extremo local en\((x_0,y_0)\), entonces\((x_0,y_0)\) es un punto crítico de\(f\).

Segunda Prueba Derivada

Considerar la función\(f(x)=x^3.\) Esta función tiene un punto crítico en\(x=0\), ya que\(f'(0)=3(0)^2=0\). Sin embargo,\(f\) no tiene un valor extremo en\(x=0\). Por lo tanto, la existencia de un valor crítico en\(x=x_0\) no garantiza un extremo local at\(x=x_0\). Lo mismo es cierto para una función de dos o más variables. Una forma en que esto puede suceder es en un punto de silla de montar. Un ejemplo de una punta de sillín aparece en la siguiente figura.

Figura\(\PageIndex{3}\): Gráfica de la función\(z=x^2−y^2\). Esta gráfica tiene un punto de sillín en el origen.

En esta gráfica, el origen es un punto de sillín. Esto se debe a que las primeras derivadas parciales de f\((x,y)=x^2−y^2\) son ambas iguales a cero en este punto, pero no es ni un máximo ni un mínimo para la función. Además, la traza vertical correspondiente a\(y=0\) es\(z=x^2\) (una parábola que se abre hacia arriba), pero la traza vertical correspondiente a\(x=0\) es\(z=−y^2\) (una parábola que se abre hacia abajo). Por lo tanto, es tanto un máximo global para un rastro como un mínimo global para otro.

Definición: Saddle Point

Dada la función\(z=f(x,y),\) el punto\(\big(x_0,y_0,f(x_0,y_0)\big)\) es un punto de sillín si ambos\(f_x(x_0,y_0)=0\) y\(f_y(x_0,y_0)=0\), pero\(f\) no tiene un extremo local en\((x_0,y_0).\)

La segunda prueba derivada para una función de una variable proporciona un método para determinar si un extremo ocurre en un punto crítico de una función. Al extender este resultado a una función de dos variables, surge un problema relacionado con el hecho de que existen, de hecho, cuatro diferentes derivadas parciales de segundo orden, aunque la igualdad de parciales mixtos reduce esto a tres. La prueba de la segunda derivada para una función de dos variables, establecida en el siguiente teorema, utiliza un discriminante\(D\) que reemplaza\(f''(x_0)\) en la prueba de la segunda derivada por una función de una variable.

Segunda Prueba Derivada

Dejar\(z=f(x,y)\) ser una función de dos variables para las cuales las derivadas parciales de primer y segundo orden son continuas en algún disco que contiene el punto\((x_0,y_0)\). Supongamos\(f_x(x_0,y_0)=0\) y\(f_y(x_0,y_0)=0.\) Definir la cantidad

\[D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−\big(f_{xy}(x_0,y_0)\big)^2. \nonumber \]

Entonces:

1. Si\(D>0\) y\(f_{xx}(x_0,y_0)>0\), entonces f tiene un mínimo local en\((x_0,y_0)\).
2. Si\(D>0\) y\(f_{xx}(x_0,y_0)<0\), entonces f tiene un máximo local en\((x_0,y_0)\).
3. Si\(D<0\), entonces\(f\) tiene un punto de sillín en\((x_0,y_0)\).
4. Si\(D=0\), entonces la prueba no es concluyente.

Ver Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): La prueba de la segunda derivada a menudo puede determinar si una función de dos variables tiene mínimos locales (a), máximos locales (b) o un punto de sillín (c).

Para aplicar la segunda prueba derivada, es necesario que primero encontremos los puntos críticos de la función. Hay varios pasos involucrados en todo el procedimiento, los cuales se describen en una estrategia de resolución de problemas.

Estrategia de Resolución de Problemas: Uso de la Prueba de Segunda Derivada para Funciones de Dos Variables

Dejar\(z=f(x,y)\) ser una función de dos variables para las cuales las derivadas parciales de primer y segundo orden son continuas en algún disco que contiene el punto\((x_0,y_0).\) Para aplicar la prueba de segunda derivada para encontrar extremos locales, utilice los siguientes pasos:

1. Determinar los puntos críticos\((x_0,y_0)\) de la función\(f\) donde\(f_x(x_0,y_0)=f_y(x_0,y_0)=0.\) Descartar cualquier punto donde al menos una de las derivadas parciales no exista.
2. Calcular el discriminante\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−\big(f_{xy}(x_0,y_0)\big)^2\) para cada punto crítico de\(f\).
3. Aplicar los cuatro casos de la prueba para determinar si cada punto crítico es un máximo local, un mínimo local o un punto de sillín, o si el teorema no es concluyente.

Ejemplo\(\PageIndex{2}\): Using the Second Derivative Test

Encuentra los puntos críticos para cada una de las siguientes funciones, y usa la segunda prueba derivada para encontrar los extremos locales:

1. \(f(x,y)=4x^2+9y^2+8x−36y+24\)
2. \(g(x,y)=\dfrac{1}{3}x^3+y^2+2xy−6x−3y+4\)

Solución

a. El paso 1 de la estrategia de resolución de problemas implica encontrar los puntos críticos de\(f\). Para ello, primero calculamos\(f_x(x,y)\) y\(f_y(x,y)\), luego establecemos cada uno de ellos igual a cero:

\[\begin{align*} f_x(x,y) &=8x+8 \\[4pt] f_y(x,y) &=18y−36. \end{align*}\]

Al establecerlos iguales a cero se obtiene el sistema de ecuaciones

\[\begin{align*} 8x+8 &=0 \\[4pt] 18y−36 &=0. \end{align*}\]

La solución a este sistema es\(x=−1\) y\(y=2\). Por lo tanto\((−1,2)\) es un punto crítico de\(f\).

El paso 2 de la estrategia de resolución de problemas implica calcular\(D.\) Para ello, primero calculamos las segundas derivadas parciales de\(f:\)

\[\begin{align*} f_{xx}(x,y) &=8 \\[4pt] f_{xy}(x,y) &=0 \\[4pt] f_{yy}(x,y) &=18. \end{align*}\]

Por lo tanto,\(D=f_{xx}(−1,2)f_{yy}(−1,2)−\big(f_{xy}(−1,2)\big)^2=(8)(18)−(0)^2=144.\)

El paso 3 establece aplicar los cuatro casos de la prueba para clasificar el comportamiento de la función en este punto crítico.

Ya\(D>0\) y\(f_{xx}(−1,2)>0,\) esto corresponde al caso 1. Por lo tanto,\(f\) tiene un mínimo local en\((−1,2)\) como se muestra en la siguiente figura.

Figura\(\PageIndex{5}\): La función\(f(x,y)\) tiene un mínimo local en\((−1,2,−16).\) Note la escala en el\(y\) eje -en esta gráfica es en miles.

b. Para el paso 1, primero calculamos\(g_x(x,y)\) y\(g_y(x,y)\), luego establecemos cada uno de ellos igual a cero:

\[\begin{align*} g_x(x,y) &=x^2+2y−6 \\[4pt] g_y(x,y) &=2y+2x−3. \end{align*}\]

Al establecerlos iguales a cero se obtiene el sistema de ecuaciones

\[\begin{align*} x^2+2y−6 &=0 \\[4pt] 2y+2x−3 &=0. \end{align*}\]

Para resolver este sistema, primero resolver la segunda ecuación para\(y\). Esto da\(y=\dfrac{3−2x}{2}\). Sustituyendo esto en la primera ecuación da

\[\begin{align*} x^2+3−2x−6 &=0 \\[4pt] x^2−2x−3 &=0 \\[4pt] (x−3)(x+1) &=0. \end{align*}\]

Por lo tanto,\(x=−1\) o\(x=3\). Al sustituir estos valores en la ecuación se\(y=\dfrac{3−2x}{2}\) obtienen los puntos críticos\(\left(−1,\frac{5}{2}\right)\) y\(\left(3,−\frac{3}{2}\right)\).

El paso 2 implica calcular las segundas derivadas parciales de\(g\):

\[\begin{align*} g_{xx}(x,y) &=2x \\[4pt] g_{xy}(x,y) &=2\\[4pt] g_{yy}(x,y) &=2. \end{align*}\]

Luego, encontramos una fórmula general para\(D\):

\[\begin{align*} D(x_0, y_0) &=g_{xx}(x_0,y_0)g_{yy}(x_0,y_0)−\big(g_{xy}(x_0,y_0)\big)^2 \\[4pt] &=(2x_0)(2)−2^2\\[4pt] &=4x_0−4.\end{align*}\]

A continuación, sustituimos cada punto crítico en esta fórmula:

\[\begin{align*} D\left(−1,\tfrac{5}{2}\right) &=(2(−1))(2)−(2)^2=−4−4=−8 \\[4pt] D\left(3,−\tfrac{3}{2}\right) &=(2(3))(2)−(2)^2=12−4=8. \end{align*}\]

En el paso 3, observamos que, aplicar Nota a punto\(\left(−1,\frac{5}{2}\right)\) lleva al caso\(3\), lo que significa que\(\left(−1,\frac{5}{2}\right)\) es un punto de sillín. Aplicar el teorema a punto\(\left(3,−\frac{3}{2}\right)\) lleva al caso\(1\), lo que significa que\(\left(3,−\frac{3}{2}\right)\) corresponde a un mínimo local como se muestra en la siguiente figura.

Figura\(\PageIndex{6}\): La función\(g(x,y)\) tiene un mínimo local y un punto de sillín.

Ejercicio\(\PageIndex{2}\)

Utilice la segunda prueba derivada para encontrar los extremos locales de la función

\[ f(x,y)=x^3+2xy−6x−4y^2. \nonumber \]

Pista

Siga la estrategia de resolución de problemas para aplicar la segunda prueba derivada.

Contestar

\(\left(\frac{4}{3},\frac{1}{3}\right)\)es un punto de sillín,\(\left(−\frac{3}{2},−\frac{3}{8}\right)\) es un máximo local.

Máximo absoluto y mínimo

Al encontrar extremos globales de funciones de una variable en un intervalo cerrado, comenzamos verificando los valores críticos sobre ese intervalo y luego evaluamos la función en los puntos finales del intervalo. Cuando se trabaja con una función de dos variables, el intervalo cerrado se reemplaza por un conjunto cerrado y delimitado. Un conjunto está delimitado si todos los puntos de ese conjunto pueden estar contenidos dentro de una bola (o disco) de radio finito. Primero, necesitamos encontrar los puntos críticos dentro del conjunto y calcular los valores críticos correspondientes. Entonces, es necesario encontrar el valor máximo y mínimo de la función en el límite del conjunto. Cuando tenemos todos estos valores, el valor de función más grande corresponde al máximo global y el valor de función más pequeño corresponde al mínimo absoluto. Primero, sin embargo, hay que estar seguros de que tales valores existen. El siguiente teorema hace esto.

Teorema de Valor Extremo

Una función continua\(f(x,y)\) en un conjunto cerrado y acotado\(D\) en el plano alcanza un valor máximo absoluto en algún punto de\(D\) y un valor mínimo absoluto en algún punto de\(D\).

Ahora que sabemos que cualquier función continua\(f\) definida en un conjunto cerrado y acotado alcanza sus valores extremos, necesitamos saber cómo encontrarlos.

Encontrar valores extremos de una función de dos variables

Supongamos que\(z=f(x,y)\) es una función diferenciable de dos variables definidas en un conjunto cerrado y delimitado\(D\). Entonces\(f\) se alcanzará el valor máximo absoluto y el valor mínimo absoluto, que son, respectivamente, los valores más grandes y más pequeños que se encuentran entre los siguientes:

1. Los valores de\(f\) en los puntos críticos de\(f\) in\(D\).
2. Los valores de\(f\) en el límite de\(D\).

La prueba de este teorema es una consecuencia directa del teorema del valor extremo y del teorema de Fermat. En particular, si cualquiera de los extremos no se encuentra en el límite de\(D\), entonces se ubica en un punto interior de\(D\). Pero un punto interior\((x_0,y_0)\) de\(D\) eso es un extremo absoluto es también un extremo local; de ahí,\((x_0,y_0)\) es un punto crítico de\(f\) por el teorema de Fermat. Por lo tanto, los únicos valores posibles para los extremos globales de\(f\) on\(D\) son los valores extremos de\(f\) en el interior o límite de\(D\).

Estrategia de resolución de problemas: encontrar valores máximos y mínimos absolutos

Dejar\(z=f(x,y)\) ser una función continua de dos variables definidas en un conjunto cerrado, acotado\(D\), y asumir\(f\) es diferenciable en\(D\). Para encontrar los valores máximos y mínimos absolutos de\(f\) on\(D\), haga lo siguiente:

1. Determinar los puntos críticos de\(f\) in\(D\).
2. Calcular\(f\) en cada uno de estos puntos críticos.
3. Determinar los valores máximo y mínimo de\(f\) en el límite de su dominio.
4. Los valores máximo y mínimo de\(f\) ocurrirán en uno de los valores obtenidos en pasos\(2\) y\(3\).

Encontrar los valores máximos y mínimos de\(f\) en el límite de\(D\) puede ser un desafío. Si el límite es un rectángulo o conjunto de líneas rectas, entonces es posible parametrizar los segmentos de línea y determinar los máximos en cada uno de estos segmentos, como se ve en Ejemplo\(\PageIndex{3}\). El mismo enfoque se puede utilizar para otras formas como círculos y elipses.

Si el límite del conjunto\(D\) es una curva más complicada definida por una función\(g(x,y)=c\) para alguna constante\(c\), y las derivadas parciales de primer orden de\(g\) existen, entonces el método de multiplicadores Lagrange puede resultar útil para determinar los extremos de\(f\) en el límite que se introduce en Lagrange Multipliers.

Ejemplo\(\PageIndex{3}\): Finding Absolute Extrema

Utilice la estrategia de resolución de problemas para encontrar los extremos absolutos de una función para determinar los extremos absolutos de cada una de las siguientes funciones:

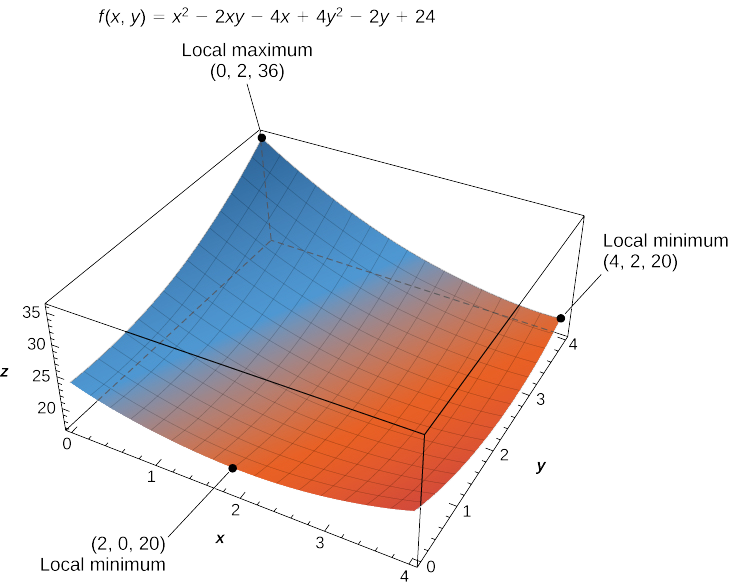
1. \(f(x,y)=x^2−2xy+4y^2−4x−2y+24\)en el dominio definido por\(0≤x≤4\) y\(0≤y≤2\)
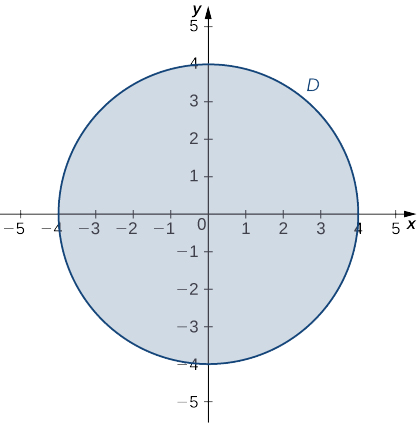
2. \(g(x,y)=x^2+y^2+4x−6y\)en el dominio definido por\(x^2+y^2≤16\)

Solución

a. Usando la estrategia de resolución de problemas, el paso\(1\) implica encontrar los puntos críticos de\(f\) en su dominio. Por lo tanto, primero calculamos\(f_x(x,y)\) y\(f_y(x,y)\), luego los establecemos cada uno igual a cero:

\[\begin{align*} f_x(x,y) &=2x−2y−4 \\[4pt] f_y(x,y) &=−2x+8y−2. \end{align*}\]

Al establecerlos iguales a cero se obtiene el sistema de ecuaciones

\[\begin{align*} 2x−2y−4 &=0\\[4pt] −2x+8y−2 &=0. \end{align*}\]

La solución a este sistema es\(x=3\) y\(y=1\). Por lo tanto\((3,1)\) es un punto crítico de\(f\). Calcular\(f(3,1)\) da\(f(3,1)=17.\)

El siguiente paso consiste en encontrar los extremos de\(f\) en el límite de su dominio. El límite de su dominio consta de cuatro segmentos de línea como se muestra en la siguiente gráfica:

Figura\(\PageIndex{7}\): Gráfica del dominio de la función\(f(x,y)=x^2−2xy+4y^2−4x−2y+24.\)

\(L_1\)es el segmento de línea que conecta\((0,0)\) y\((4,0)\), y puede ser parametrizado por las ecuaciones\(x(t)=t,y(t)=0\) para\(0≤t≤4\). Definir\(g(t)=f\big(x(t),y(t)\big)\). Esto da\(g(t)=t^2−4t+24\). Diferenciar\(g\) conduce a\(g′(t)=2t−4.\) Por lo tanto,\(g\) tiene un valor crítico at\(t=2\), que corresponde al punto\((2,0)\). El cálculo\(f(2,0)\) da el\(z\) -valor\(20\).

\(L_2\)es el segmento de línea que conecta\((4,0)\) y\((4,2)\), y puede ser parametrizado por las ecuaciones\(x(t)=4,y(t)=t\) para\(0≤t≤2.\) Nuevamente, definir\(g(t)=f\big(x(t),y(t)\big).\) Esto da\(g(t)=4t^2−10t+24.\) Entonces,\(g′(t)=8t−10\). g tiene un valor crítico at\(t=\frac{5}{4}\), que corresponde al punto\(\left(0,\frac{5}{4}\right).\) Calculando \(f\left(0,\frac{5}{4}\right)\)da el\(z\) valor\(27.75\) -.

\(L_3\)es el segmento de línea que conecta\((0,2)\) y\((4,2)\), y puede ser parametrizado por las ecuaciones\(x(t)=t,y(t)=2\) para\(0≤t≤4.\) Nuevamente, definir\(g(t)=f\big(x(t),y(t)\big).\) Esto da\(g(t)=t^2−8t+36.\) El valor crítico corresponde al punto\((4,2).\) Entonces, calculando\(f(4,2)\) da el\(z\) -valor \(20\).

\(L_4\)es el segmento de línea que conecta\((0,0)\) y\((0,2)\), y puede ser parametrizado por las ecuaciones\(x(t)=0,y(t)=t\) para\(0≤t≤2.\) Esta vez,\(g(t)=4t^2−2t+24\) y el valor crítico\(t=\frac{1}{4}\) corresponde al punto\(\left(0,\frac{1}{4}\right)\). El cálculo\(f\left(0,\frac{1}{4}\right)\) da el\(z\) -valor\(23.75.\)

También necesitamos encontrar los valores de\(f(x,y)\) en los rincones de su dominio. Estas esquinas se encuentran en\((0,0),(4,0),(4,2)\) y\((0,2)\):

\[\begin{align*} f(0,0) &=(0)^2−2(0)(0)+4(0)^2−4(0)−2(0)+24=24 \\[4pt] f(4,0) &=(4)^2−2(4)(0)+4(0)^2−4(4)−2(0)+24=24 \\[4pt] f(4,2) &=(4)^2−2(4)(2)+4(2)^2−4(4)−2(2)+24=20\\[4pt] f(0,2) &=(0)^2−2(0)(2)+4(2)^2−4(0)−2(2)+24=36. \end{align*}\]

El valor máximo absoluto es\(36\), que ocurre en\((0,2)\), y el valor mínimo global es\(20\), que ocurre en ambos\((4,2)\) y\((2,0)\) como se muestra en la siguiente figura.

Figura\(\PageIndex{8}\): La función\(f(x,y)\) tiene dos mínimos globales y un máximo global sobre su dominio.

b. Usando la estrategia de resolución de problemas, el paso\(1\) implica encontrar los puntos críticos de\(g\) en su dominio. Por lo tanto, primero calculamos\(g_x(x,y)\) y\(g_y(x,y)\), luego los establecemos cada uno igual a cero:

\[\begin{align*} g_x(x,y) &=2x+4 \\[4pt] g_y(x,y) &=2y−6. \end{align*}\]

Al establecerlos iguales a cero se obtiene el sistema de ecuaciones

\[\begin{align*} 2x+4 &=0 \\[4pt] 2y−6 &=0. \end{align*}\]

La solución a este sistema es\(x=−2\) y\(y=3\). Por lo tanto,\((−2,3)\) es un punto crítico de\(g\). Calculando\(g(−2,3),\) obtenemos

\[g(−2,3)=(−2)^2+3^2+4(−2)−6(3)=4+9−8−18=−13. \nonumber \]

El siguiente paso consiste en encontrar los extremos de g en el límite de su dominio. El límite de su dominio consiste en un círculo de radio\(4\) centrado en el origen como se muestra en la siguiente gráfica.

Figura\(\PageIndex{9}\): Gráfica del dominio restringido de la función\(g(x,y)=x^2+y^2+4x−6y\).

El límite del dominio de se\(g\) puede parametrizar usando las funciones\(x(t)=4\cos t,\, y(t)=4\sin t\) para\(0≤t≤2π\). Definir\(h(t)=g\big(x(t),y(t)\big):\)

\[\begin{align*} h(t) &=g\big(x(t),y(t)\big) \\[4pt] &=(4\cos t)^2+(4\sin t)^2+4(4\cos t)−6(4\sin t) \\[4pt] &=16\cos^2t+16\sin^2t+16\cos t−24\sin t\\[4pt] &=16+16\cos t−24\sin t. \end{align*}\]

El ajuste\(h′(t)=0\) conduce a

\[\begin{align*} −16\sin t−24\cos t &=0 \\[4pt] −16\sin t &=24\cos t\\[4pt] \dfrac{−16\sin t}{−16\cos t} &=\dfrac{24\cos t}{−16\cos t} \\[4pt] \tan t &=−\dfrac{3}{2}. \end{align*}\]

Esta ecuación tiene dos soluciones a lo largo del intervalo\(0≤t≤2π\). Uno es\(t=π−\arctan (\frac{3}{2})\) y el otro lo es\(t=2π−\arctan (\frac{3}{2})\). Para el primer ángulo,

\[\begin{align*} \sin t &=\sin(π−\arctan(\tfrac{3}{2}))=\sin (\arctan (\tfrac{3}{2}))=\dfrac{3\sqrt{13}}{13} \\[4pt] \cos t &=\cos (π−\arctan (\tfrac{3}{2}))=−\cos (\arctan (\tfrac{3}{2}))=−\dfrac{2\sqrt{13}}{13}. \end{align*}\]

Por lo tanto\(y(t)=4\sin t=\frac{12\sqrt{13}}{13}\),\(x(t)=4\cos t =−\frac{8\sqrt{13}}{13}\) y, así\(\left(−\frac{8\sqrt{13}}{13},\frac{12\sqrt{13}}{13}\right)\) es un punto crítico en el límite y

\[\begin{align*} g\left(−\tfrac{8\sqrt{13}}{13},\tfrac{12\sqrt{13}}{13}\right) &=\left(−\tfrac{8\sqrt{13}}{13}\right)^2+\left(\tfrac{12\sqrt{13}}{13}\right)^2+4\left(−\tfrac{8\sqrt{13}}{13}\right)−6\left(\tfrac{12\sqrt{13}}{13}\right) \\[4pt] &=\frac{144}{13}+\frac{64}{13}−\frac{32\sqrt{13}}{13}−\frac{72\sqrt{13}}{13} \\[4pt] &=\frac{208−104\sqrt{13}}{13}≈−12.844. \end{align*}\]

Para el segundo ángulo,

\[\begin{align*} \sin t &=\sin (2π−\arctan (\tfrac{3}{2}))=−\sin (\arctan (\tfrac{3}{2}))=−\dfrac{3\sqrt{13}}{13} \\[4pt] \cos t &=\cos (2π−\arctan (\tfrac{3}{2}))=\cos (\arctan (\tfrac{3}{2}))=\dfrac{2\sqrt{13}}{13}. \end{align*}\]

Por lo tanto\(y(t)=4\sin t=−\frac{12\sqrt{13}}{13}\),\(x(t)=4\cos t=\frac{8\sqrt{13}}{13}\) y, así\(\left(\frac{8\sqrt{13}}{13},−\frac{12\sqrt{13}}{13}\right)\) es un punto crítico en el límite y

\[\begin{align*} g\left(\tfrac{8\sqrt{13}}{13},−\tfrac{12\sqrt{13}}{13}\right) &=\left(\tfrac{8\sqrt{13}}{13}\right)^2+\left(−\tfrac{12\sqrt{13}}{13}\right)^2+4\left(\tfrac{8\sqrt{13}}{13}\right)−6\left(−\tfrac{12\sqrt{13}}{13}\right) \\[4pt] &=\dfrac{144}{13}+\dfrac{64}{13}+\dfrac{32\sqrt{13}}{13}+\dfrac{72\sqrt{13}}{13}\\[4pt] &=\dfrac{208+104\sqrt{13}}{13}≈44.844. \end{align*}\]

El mínimo absoluto de\(g\) es el\(−13,\) que se alcanza en el punto\((−2,3)\), que es un punto interior de\(D\). El máximo absoluto de\(g\) es aproximadamente igual a 44.844, que se alcanza en el punto límite\(\left(\frac{8\sqrt{13}}{13},−\frac{12\sqrt{13}}{13}\right)\). Estos son los extremos absolutos de\(g\) on\(D\) como se muestra en la siguiente figura.

Figura\(\PageIndex{10}\): La función\(f(x,y)\) tiene un mínimo local y un máximo local.

Ejercicio\(\PageIndex{3}\):

Utilizar la estrategia de resolución de problemas para encontrar los extremos absolutos de una función para encontrar el extremo absoluto de la función

\[f(x,y)=4x^2−2xy+6y^2−8x+2y+3 \nonumber \]

en el dominio definido por\(0≤x≤2\) y\(−1≤y≤3.\)

Pista

Calcular\(f_x(x,y)\) y\(f_y(x,y)\), y establecerlos iguales a cero. Después, calcular\(f\) para cada punto crítico y encontrar los extremos de\(f\) en el límite de\(D\).

Contestar

El mínimo absoluto ocurre en\((1,0): f(1,0)=−1.\)

El máximo absoluto ocurre en\((0,3): f(0,3)=63.\)

Ejemplo\(\PageIndex{4}\): Profitable Golf Balls

\(T\)La compañía Pro- ha desarrollado un modelo de ganancias que depende del número\(x\) de pelotas de golf vendidas al mes (medido en miles), y del número de horas al mes de publicidad\(y\), según la función

\[ z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]

donde\(z\) se mide en miles de dólares. El número máximo de pelotas de golf que se pueden producir y vender es\(50,000\), y el número máximo de horas de publicidad que se pueden comprar es\(25\). Encuentra los valores de\(x\) y\(y\) que maximizan el beneficio, y encuentra el máximo beneficio.

Figura\(\PageIndex{11}\): (crédito: modificación de obra por oatsy40, Flickr)

Solución

Usando la estrategia de resolución de problemas, el paso\(1\) implica encontrar los puntos críticos de\(f\) en su dominio. Por lo tanto, primero calculamos\(f_x(x,y)\) y\(f_y(x,y),\) luego establecemos cada uno igual a cero:

\[\begin{align*} f_x(x,y) &=48−2x−2y \\[4pt] f_y(x,y) &=96−2x−18y. \end{align*}\]

Al establecerlos iguales a cero se obtiene el sistema de ecuaciones

\[\begin{align*} 48−2x−2y &=0 \\[4pt] 96−2x−18y &=0. \end{align*}\]

La solución a este sistema es\(x=21\) y\(y=3\). Por lo tanto\((21,3)\) es un punto crítico de\(f\). Calcular\(f(21,3)\) da\(f(21,3)=48(21)+96(3)−21^2−2(21)(3)−9(3)^2=648.\)

El dominio de esta función es\(0≤x≤50\) y\(0≤y≤25\) como se muestra en la siguiente gráfica.

Figura\(\PageIndex{12}\): Gráfica del dominio de la función\(f(x,y)=48x+96y−x^2−2xy−9y^2.\)

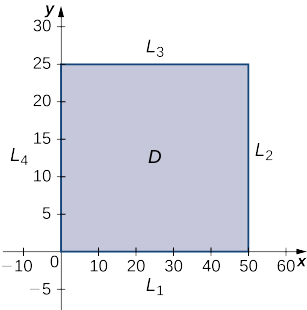
\(L_1\)es el segmento de línea que conecta\((0,0)\)\((50,0),\) y y puede ser parametrizado por las ecuaciones\(x(t)=t,y(t)=0\) para Luego\(0≤t≤50.\) definimos\(g(t)=f(x(t),y(t)):\)

\[\begin{align*} g(t) &=f(x(t),y(t)) \\[4pt] &=f(t,0)\\[4pt] &=48t+96(0)−y^2−2(t)(0)−9(0)^2\\[4pt] &=48t−t^2. \end{align*}\]

El ajuste\(g′(t)=0\) produce el punto crítico\(t=24,\) que corresponde al punto\((24,0)\) en el dominio de\(f\). Calcular\(f(24,0)\) da\(576.\)

\(L_2\)es el segmento de línea que conecta\((50,0)\) y\((50,25)\), y puede ser parametrizado por las ecuaciones\(x(t)=50,y(t)=t\) para\(0≤t≤25\). Una vez más, definimos\(g(t)=f\big(x(t),y(t)\big):\)

\[\begin{align*} g(t) &=f\big(x(t),y(t)\big)\\[4pt] &=f(50,t)\\[4pt] &=48(50)+96t−50^2−2(50)t−9t^2 \\[4pt] &=−9t^2−4t−100. \end{align*}\]

Esta función tiene un punto crítico en\(t =−\frac{2}{9}\), que corresponde al punto\((50,−29)\). Este punto no está en el dominio de\(f\).

\(L_3\)es el segmento de línea que conecta\((0,25)\) y\((50,25)\), y puede ser parametrizado por las ecuaciones\(x(t)=t,y(t)=25\) para\(0≤t≤50\). Definimos\(g(t)=f\big(x(t),y(t)\big)\):

\[\begin{align*} g(t) &=f\big(x(t),y(t)\big)\\[4pt] &=f(t,25) \\[4pt] &=48t+96(25)−t^2−2t(25)−9(25^2) \\[4pt] &=−t^2−2t−3225. \end{align*}\]

Esta función tiene un punto crítico en\(t=−1\), que corresponde al punto\((−1,25),\) que no está en el dominio.

\(L_4\)es el segmento de línea que se conecta\((0,0)\) a\((0,25)\), y puede ser parametrizado por las ecuaciones\(x(t)=0,y(t)=t\) para\(0≤t≤25\). Definimos\(g(t)=f\big(x(t),y(t)\big)\):

\[\begin{align*} g(t) &=f\big(x(t),y(t)\big) \\[4pt] &=f(0,t) \\[4pt] &=48(0)+96t−(0)^2−2(0)t−9t^2 \\[4pt] &=96t−9t^2. \end{align*}\]

Esta función tiene un punto crítico en\(t=\frac{16}{3}\), que corresponde al punto\(\left(0,\frac{16}{3}\right)\), que se encuentra en el límite del dominio. Calcular\(f\left(0,\frac{16}{3}\right)\) da\(256\).

También necesitamos encontrar los valores de\(f(x,y)\) en los rincones de su dominio. Estas esquinas se encuentran en\((0,0),(50,0),(50,25)\) y\((0,25)\):

\[\begin{align*} f(0,0) &=48(0)+96(0)−(0)^2−2(0)(0)−9(0)^2=0\\[4pt] f(50,0) &=48(50)+96(0)−(50)^2−2(50)(0)−9(0)^2=−100 \\[4pt] f(50,25) &=48(50)+96(25)−(50)^2−2(50)(25)−9(25)^2=−5825 \\[4pt] f(0,25) &=48(0)+96(25)−(0)^2−2(0)(25)−9(25)^2=−3225. \end{align*}\]

El valor máximo es\(648\), que ocurre en\((21,3)\). Por lo tanto,\($648,000\) se obtiene una ganancia máxima de cuando se venden pelotas de\(21,000\) golf y se compran\(3\) horas de publicidad al mes como se muestra en la siguiente figura.

Figura\(\PageIndex{13}\): La función de ganancia\(f(x,y)\) tiene un máximo en\((21,3,648)\).

Conceptos clave

• Un punto crítico de la función\(f(x,y)\) es cualquier punto\((x_0,y_0)\) donde cualquiera\(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), o al menos uno de\(f_x(x_0,y_0)\) y\(f_y(x_0,y_0)\) no existan.
• Un punto de silla de montar es un punto\((x_0,y_0)\) donde\(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), pero no\(f(x_0,y_0)\) es ni un máximo ni un mínimo en ese punto.
• Para encontrar extremos de funciones de dos variables, primero encontrar los puntos críticos, luego calcular el discriminante y aplicar la segunda prueba derivada.

Ecuaciones Clave

• Discriminante

\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−(f_{xy}(x_0,y_0))^2\)

Glosario

punto crítico de una función de dos variables

el punto\((x_0,y_0)\) se denomina punto crítico de\(f(x,y)\) si se mantiene una de las dos condiciones siguientes:

1. \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)

2. Al menos uno de\(f_x(x_0,y_0)\) y\(f_y(x_0,y_0)\) no existen

discriminante

el discriminante de la función\(f(x,y)\) viene dado por la fórmula\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−(f_{xy}(x_0,y_0))^2\)

punto de sillín

dada la función\(z=f(x,y),\) el punto\((x_0,y_0,f(x_0,y_0))\) es un punto de sillín si ambos\(f_x(x_0,y_0)=0\) y\(f_y(x_0,y_0)=0\), pero\(f\) no tiene un extremo local en\((x_0,y_0)\)