4.2: Propiedades de Integrales de Línea
- Page ID
- 111301
Sabemos por la sección anterior que para integrales de línea de funciones de valor real (campos escalares), invertir la dirección en la que se toma la integral a lo largo de una curva no cambia el valor de la integral de línea:
\[\int_C f (x, y)\,ds = \int_{-C} f (x, y)\,ds \label{Eq4.17}\]
Sin embargo, para integrales de línea de campos vectoriales, el valor sí cambia. Para ver esto, deja\(\textbf{f}(x, y) = P(x, y)\textbf{i} +Q(x, y)\textbf{j}\) ser un campo vectorial, con\(P\) y funciones\(Q\) continuamente diferenciables. Dejar\(C\) ser una curva suave parametrizada por\(x = x(t), y = y(t), a ≤ t ≤ b\), con vector de posición\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}\) (usualmente abreviaremos esto diciendo que\(C : \textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}\) es una curva suave). Sabemos que la curva\(−C\) atravesada en sentido contrario es parametrizada por\(x = x(a+ b − t), y = y(a+ b − t), a ≤ t ≤ b\). Entonces
\[\nonumber \begin{align} \int_{-C} P(x, y)\,dx&=\int_a^b P(x(a+ b − t), y(a+ b − t))\dfrac{d }{dt}(x(a+ b − t))\,dt \\[4pt] \nonumber &=\int_a^b P(x(a+ b − t), y(a+ b − t)) (−x ′ (a+ b − t))\,dt\text{ (by the Chain Rule)} \\[4pt] \nonumber &=\int_a^b P(x(u), y(u)) (−x ′ (u)) (−du)\text{ (by letting }u = a+ b − t) \\[4pt] \nonumber &= \int_a^b P(x(u), y(u)) x ′ (u)\,du \\[4pt] \nonumber &=-\int_a^b P(x(u), y(u)) x ′ (u)\,du,\text{ since }\int_a^b = -\int_a^b,\text{ so} \\[4pt] \nonumber \int_{-C} P(x, y)\,dx &= -\int_{-C} P(x, y)\,dx \\[4pt] \end{align}\]
ya que solo estamos usando una letra diferente\((u)\) para la línea integral a lo largo\(C\). Un argumento similar muestra que
\[\nonumber \int_{-C} Q(x, y)\,d y = -\int_C Q(x, y)\,d y ,\]
y por lo tanto
\[\nonumber \begin{align} \int_{-C}\textbf{f}\cdot d\textbf{r} &= \int_{-C} P(x, y)\,dx+\int_{-C}Q(x, y)\,d y \\[4pt] \nonumber &=-\int_C P(x, y)\,dx + - \int_C Q(x, y)\,d y \\[4pt] \nonumber &=- \left ( \int_C P(x, y)\,dx+ \int_C Q(x, y)\,d y \right ) \\[4pt] \int_{-C} \textbf{f}\cdot d\textbf{r} &= -\int_C \textbf{f}\cdot d\textbf{r}.\label{Eq4.18} \\[4pt] \end{align}\]
La fórmula anterior se puede interpretar en términos del trabajo realizado por una fuerza\(\textbf{f}(x, y)\) (tratada como un vector) que mueve un objeto a lo largo de una curva\(C\): el trabajo total realizado moviendo el objeto a lo largo\(C\) de su punto inicial a su punto terminal, y luego de vuelta al punto inicial moviéndose hacia atrás a lo largo del mismo camino, es cero. Esto se debe a que cuando la fuerza se considera como un vector, se contabiliza la dirección.
La discusión anterior muestra la importancia de tener siempre en cuenta la dirección de la curva al usar integrales de línea de campos vectoriales. Por esta razón, las curvas en integrales de línea a veces se denominan curvas dirigidas o curvas orientadas.
Recordemos que nuestra definición de una integral de línea requería que tuviéramos una parametrización\(x = x(t), y = y(t), a ≤ t ≤ b\) para la curva\(C\). Pero como sabemos, cualquier curva tiene infinitamente muchas parametrizaciones. Entonces, ¿podríamos obtener un valor diferente para una integral de línea usando alguna otra parametrización de\(C\), digamos,\(x = \tilde x(u), y = \tilde y(u), c ≤ u ≤ d\)? De ser así, esto significaría que nuestra definición no está bien definida. Por suerte, resulta que el valor de una integral de línea de un campo vectorial no cambia siempre y cuando la dirección de la curva\(C\) se conserve por cualquier parametrización que se elija:
Teorema 4.2
Dejar\(\textbf{f}(x, y) = P(x, y)\textbf{i} +Q(x, y)\textbf{j}\) ser un campo vectorial, y dejar\(C\) ser una curva suave parametrizada por\(x = x(t), y = y(t), a ≤ t ≤ b\). Supongamos que\(t = α(u) \text{ for }c ≤ u ≤ d\), tal que\(a = α(c), b = α(d), \text{ and }α ′ (u) > 0\) en el intervalo abierto\((c,d)\) (es decir,\(α(u)\) está aumentando estrictamente en\([c,d]\)). Entonces\(\int_C \textbf{f}\cdot d\textbf{r}\) tiene el mismo valor para las parametrizaciones\(x = x(t), y = y(t), a ≤ t ≤ b \text{ and }x = \tilde x(u) = x(α(u)), y = \tilde y(u) = y(α(u)), c ≤ u ≤ d\).
Prueba: Ya que\(α(u)\) es estrictamente creciente y mapas\([c,d] \text{ onto }[a,b]\), entonces sabemos que\(t = α(u)\) tiene una función inversa\(u = α^{−1} (t)\) definida sobre\([a,b]\) tal que\(c = α^{−1} (a), d = α^{−1} (b), \text{ and }\dfrac{du}{dt} = \dfrac{1}{ α′ (u)}\). También,\(dt = α ′ (u)\,du\), y por la regla de la cadena
\[\nonumber \tilde x′ (u) = \dfrac{d\tilde x}{ du} = \dfrac{d}{ du} (x(α(u)))=\dfrac{ dx}{ dt}\dfrac{ dt}{ du} = x ′ (t)α ′ (u) \Rightarrow x ′ (t) = \dfrac{\tilde x ′ (u)}{ α′ (u)} \]
por lo que hacer la sustitución\(t = α(u)\) da
\[\nonumber \begin{align}\int_a^b P(x(t), y(t)) x ′ (t)\,dt &= \int_{α^{−1} (a)}^{α^{−1} (b)} P(x(α(u)), y(α(u)))\dfrac{\tilde x ′ (u)}{ α′ (u)} (α ′ (u)\,du) \\[4pt] \nonumber &= \int_c^d P(\tilde x(u), \tilde y(u)) \tilde x ′ (u)du , \\[4pt] \end{align}\]
lo que muestra que\(\int_C P(x, y)\,dx\) tiene el mismo valor para ambas parametrizaciones. Un argumento similar muestra que\(\int_C Q(x, y)\,d y\) tiene el mismo valor para ambas parametrizaciones, y por lo tanto\(\int_C \textbf{f} \cdot d\textbf{r}\) tiene el mismo valor.
Observe que la condición\(α ′ (u) > 0\) en el Teorema 4.2 significa que las dos parametrizaciones se mueven a lo largo\(C\) en la misma dirección. Ese no fue el caso con la parametrización “inversa”\(−C: \text{ for }u = a+ b − t\) porque tenemos\(t = α(u) = a+ b − u \Rightarrow α ′ (u) = −1 < 0\).
Ejemplo 4.4
Evaluar la integral\(\int_C (x^2 + y^2 )\,dx + 2x y \,d y\) de línea del Ejemplo 4.2, Sección 4.1, a lo largo de la curva\(C : x = t, y = 2t^2 , 0 ≤ t ≤ 1\), donde\(t = \sin u \text{ for }0 ≤ u ≤ π/2\).
Solución
Primero, nos damos cuenta de eso\(0 = \sin 0, 1 = sin(π/2)\), y\(\dfrac{dt}{du} = \cos u > 0 \text{ on }(0,π/2)\). Entonces por el Teorema 4.2 sabemos que si C es parametrizado por
\[\nonumber x = \sin u ,\quad y = 2\sin^2 u ,\quad 0 ≤ u ≤ π/2\]
entonces\(\int_C (x^2+ y^2 )\,dx+2x y \,d y\) debería tener el mismo valor que encontramos en el Ejemplo 4.2, es decir, 13 3. Y de hecho podemos verificar esto:
\[\nonumber \begin{align} \int_C (x^2 + y^2 )\,dx+2x y \,d y &=\int_0^{2\pi} \left ( (\sin^2 u +(2\sin^2 u)^2 )\cos u +2(\sin u)(2\sin^2 u)4\sin u \cos u \right )\,du \\[4pt] \nonumber &=\int_0^{\pi/2} \left ( \sin^2 u +20\sin^4 u \right )\cos u \,du \\[4pt] \nonumber &= \dfrac{ \sin^3 u}{3} + 4\sin^5 u \Big |_0^{\pi/2} \\[4pt] \nonumber &=\dfrac{1}{3} +4=\dfrac{13}{3} \\[4pt] \end{align}\]
En otras palabras, la integral de línea no cambia tanto\(t\) si\(u\) es el parámetro para\(C\).
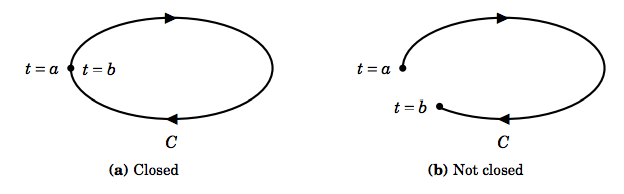
Una curva cerrada simple es una curva cerrada que no se intersecta sola. Tenga en cuenta que cualquier curva cerrada puede considerarse como una unión de curvas cerradas simples (piense en los bucles en una figura ocho). Utilizamos la notación especial
\[\nonumber \oint_C f (x, y)\,ds \text{ and }\oint_C \textbf{f}\cdot d\textbf{r}\]
para denotar integrales de línea de campos escalar y vectoriales, respectivamente, a lo largo de curvas cerradas. En algunos textos más antiguos es posible que vea la notación para indicar una integral de línea que atraviesa una curva cerrada en sentido antihorario o en sentido horario, respectivamente.
para indicar una integral de línea que atraviesa una curva cerrada en sentido antihorario o en sentido horario, respectivamente.
Hasta el momento, los ejemplos que hemos visto de integrales de línea (por ejemplo Ejemplo 4.2) han tenido el mismo valor para diferentes curvas que unen el punto inicial al punto terminal. Es decir, la línea integral ha sido independiente del camino que une los dos puntos. Como mencionamos antes, no siempre es así. El siguiente teorema da una condición necesaria y suficiente para esta independencia de camino:
Teorema 4.3
En una región\(R\), la integral de línea\(\int_C \textbf{f}\cdot d\textbf{r}\) es independiente de la trayectoria entre dos puntos cualesquiera en\(R\) si y solo si\(\oint_C \textbf{f}\cdot d\textbf{r} = 0\) por cada curva cerrada\(C\) que está contenida en\(R\).
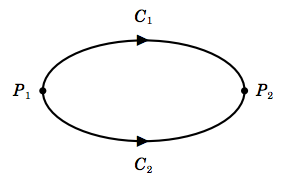
\[\nonumber \begin{align} \int_{C_1}\textbf{f}\cdot d\textbf{r} &=\int_{C_2}\textbf{f}\cdot d\textbf{r} \\[4pt] \nonumber \int_{C_1}\textbf{f}\cdot d\textbf{r} - \int_{C_2}\textbf{f}\cdot d\textbf{r} &=0 \\[4pt] \nonumber \int_{C_1} \textbf{f}\cdot d\textbf{r}+\int_{-C_2}\textbf{f}\cdot d\textbf{r} &=0,\text{ so } \\[4pt] \nonumber \oint_C \textbf{f}\cdot d\textbf{r} &= 0 \\[4pt] \end{align}\]
desde\(C = C_1 \cup −C_2 \tag{\(\textbf{QED}\)}\).
Claramente, el teorema anterior no da una forma práctica de determinar la independencia del camino, ya que es imposible verificar las integrales de línea alrededor de todas las curvas cerradas posibles en una región. Lo que hace principalmente es dar una idea de la forma en que se comportan las integrales de línea y cómo se pueden relacionar las integrales de línea aparentemente no relacionadas (en este caso, una integral de línea específica entre dos puntos y todas las integrales de línea alrededor de curvas cerradas).
Para un método más práctico para determinar la independencia de ruta, primero necesitamos una versión de la Regla de Cadena para funciones multivariables:
Teorema 4.4. (Regla de Cadena)
Si\(z = f (x, y)\) es una función continuamente diferenciable de\(x \text{ and }y\), y ambas\(x = x(t) \text{ and }y = y(t)\) son funciones diferenciables de\(t\), entonces\(z\) es una función diferenciable de\(t\), y
\[\dfrac{dz}{dt} = \dfrac{∂z}{∂x}\dfrac{ dx}{dt} + \dfrac{∂z}{∂y}\dfrac{ d y}{ dt}\label{Eq4.19}\]
en todos los puntos donde se definan las derivadas de la derecha.
La prueba es prácticamente idéntica a la prueba del Teorema 2.2 de la Sección 2.4 (que utiliza el Teorema del Valor Medio), por lo que la omitimos. Ahora usaremos esta Regla de Cadena para probar la siguiente condición suficiente para la independencia de ruta de las integrales de línea:
Ejercicio 4.5
Dejar\(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\) ser un campo vectorial en alguna región\(R\), con funciones\(P \text{ and }Q\) continuamente diferenciables encendidas\(R\). Dejar\(C\) ser una curva suave en\(R\) parametrizado por\(x = x(t), y = y(t), a ≤ t ≤ b\). Supongamos que hay una función de valor real\(F(x, y)\) tal que\(\nabla F = \textbf{f} \text{ on }R\). Entonces
\[\int_C \textbf{f}\cdot d\textbf{r} = F(B) − F(A) ,\label{Eq4.20}\]
donde\(A = (x(a), y(a)) \text{ and }B = (x(b), y(b))\) están los puntos finales de\(C\). Así, la integral de línea es independiente de la ruta entre sus puntos finales, ya que depende únicamente de los valores de\(F\) en esos puntos finales.
Prueba: Por definición de R\(\int_C \textbf{f}\cdot d\textbf{r}\), tenemos
\[\nonumber \begin{align} \int_C \textbf{f}\cdot d\textbf{r} &=\int_a^b \left ( P(x(t), y(t)) x ′ (t)+Q(x(t), y(t)) y ′ (t) \right ) \,dt \\[4pt] \nonumber &=\int_a^b \left ( \dfrac{∂F}{∂x} \dfrac{dx}{ dt} + \dfrac{∂F}{∂y}\dfrac{ d y}{ dt} \right ) \,dt \text{ since } \nabla F = \textbf{f} \Rightarrow \dfrac{∂F}{ ∂x} = P \text{ and }\dfrac{∂F}{ ∂y} = Q) \\[4pt] \nonumber &=\int_a^b F ′ (x(t), y(t))\,dt \text{(by the Chain Rule in Theorem 4.4)} \\[4pt] \nonumber &=F(x(t), y(t)) \Big |_a^b = F(B) − F(A) \\[4pt] \end{align}\]
por el Teorema Fundamental del Cálculo\(\tag{\(\textbf{QED}\)}\).
El Teorema 4.5 puede considerarse como la versión integral lineal del Teorema Fundamental del Cálculo. Una función de valor real\(F(x, y)\) tal que\(\nabla F(x, y) = f(x, y)\) se llama potencial para f. Un campo vectorial conservador es aquel que tiene potencial.
Ejemplo 4.5
Recordemos de los Ejemplos 4.2 y 4.3 de la Sección 4.1 que\(\int_C (x^2 + y^2 )\,dx + 2x y \,d y\) se encontró que la integral de línea tenía el valor\(\dfrac{13}{3}\) para tres curvas diferentes que\(C\) iban del punto\((0,0)\) al punto\((1,2)\). Utilice el Teorema 4.5 para mostrar que esta integral de línea es de hecho independiente del camino.
Solución
Necesitamos encontrar una función de valor real\(F(x, y)\) tal que
\[\nonumber \dfrac{∂F}{ ∂x} = x^2+y^2 \text{ and }\dfrac{∂F}{∂y}=2xy.\]
Supongamos que\(\dfrac{∂F}{∂x} = x^2 + y^2\), entonces debemos tener\(F(x, y) = \dfrac{1}{3} x^3 + x y^2 + g(y)\) para alguna función\(g(y)\). Así\(\dfrac{∂F}{∂y} = 2x y+ g ′ (y)\) satisface la condición\(\dfrac{∂F}{∂y} = 2x y \text{ if} g ′ (y) = 0\), es decir\(g(y) = K\), donde\(K\) es una constante. Ya que cualquier elección para\(K\) va a hacer (¿por qué?) , elegimos\(K = 0\). Así,\(F(x, y) \text{ for }\textbf{f}(x, y) = (x^2 + y^2 )\textbf{i}+2x y\textbf{j}\) existe un potencial, a saber
\[\nonumber F(x, y) = \dfrac{1}{3} x^3 + x y^2 .\]
De ahí que la integral de línea\(\int_C(x^2 + y^ 2 )\,dx+2x y \,d y\) sea independiente del camino. Tenga en cuenta que también podemos verificar que el valor de la línea integral de f a lo largo de cualquier curva que\(C\) vaya desde siempre\((0,0) \text{ to }(1,2)\) será\(\dfrac{13}{3}\), ya que por Teorema 4.5
\[\nonumber \int_C \textbf{f}\cdot d\textbf{r}=F(1,2) − F(0,0) = \dfrac{1}{3}(1)^3 +(1)(2)^2 -−(0+0) =\dfrac{1}{3}+4=\dfrac{13}{3}.\]
Una consecuencia del Teorema 4.5 en el caso especial donde\ C\) es una curva cerrada, de manera que los puntos finales\(A \text{ and }B\) son el mismo punto, es el siguiente corolario importante:
Corolario 4.6.
Si un campo vectorial f tiene un potencial en una región\(R\), entonces\(\oint_C \textbf{f}\cdot d\textbf{r} = 0\) para cualquier curva cerrada\(C\) en\(R\) (es decir,\(\oint_C \nabla F \cdot d\textbf{r} = 0\) para cualquier función de valor real\(F(x, y))\).
Ejemplo 4.6
Evaluar\(\oint_C x \,dx+ y\, d y\) para\(C : x = 2\cos t, y = 3\sin t, 0 ≤ t ≤ 2π\).
Solución:
El campo vectorial\(\textbf{f}(x, y) = x\textbf{i}+ y\textbf{j} \text{ has a potential }F(x, y)\):
\[\nonumber \begin{align}&\dfrac{∂F}{∂x} = x \Rightarrow F(x, y) =\dfrac{1}{2}x^2+g(y) ,\text{ so} \\[4pt] \nonumber &\dfrac{∂F}{∂y}=y \Rightarrow g ′ (y) = y \Rightarrow g(y) = \dfrac{1}{2}y^2+K \\[4pt] \end{align}\]
para cualquier constante\(K, \text{ so }F(x, y) = \dfrac{1}{2} x^2 + \dfrac{1}{2} y^2\) es un potencial para\(f(x, y)\). Por lo tanto,
\[\nonumber \oint_C x\,dx+y\,dy =\oint_C \textbf{f}\cdot d\textbf{r} =0\]
por Corolario 4.6, ya que la curva\(C\) está cerrada (es la elipse\(\dfrac{x^2}{ 4} + \dfrac{y^2}{ 9} = 1)\).


