6.1: Introducción a las funciones

Ejercicio\(\PageIndex{1}\)

Vista previa Actividad 1 (Funciones de cursos anteriores)
Uno de los conceptos más importantes en las matemáticas modernas es el de una función. En cursos previos de matemáticas, a menudo hemos pensado en una función como una especie de regla de entrada-salida que asigna exactamente una salida a cada entrada. Entonces en este contexto, una función puede ser pensada como un procedimiento para asociarse con cada elemento de algún conjunto, llamado el dominio de la función, exactamente un elemento de otro conjunto, llamado el codominio de la función. Este procedimiento puede considerarse una regla de entrada-salida. La función toma la entrada, que es un elemento del dominio, y produce una salida, que es un elemento del codominio. En cálculo y precálculo, las entradas y salidas fueron casi siempre números reales. Entonces la notaciónf\(f(x) = x^2 sin x\) significa lo siguiente:

• \(f\)es el nombre de la función.
• \(f(x)\)es un número real. Es la salida de la función cuando la entrada es el número real\(x\). Por ejemplo,
  \[\begin{array} {rcl} {f(\dfrac{\pi}{2})} &= & {(\dfrac{\pi}{2})^2 sin(\dfrac{\pi}{2})} \\ {} &= & {\dfrac{\pi ^2}{4} \cdot 1} \\ {} &= & {\dfrac{\pi ^2}{4}.} \end{array}\]

Para esta función, se entiende que el dominio de la función es el conjunto\(\mathbb{R}\) de todos los números reales. Ante esta situación, pensamos en el dominio como el conjunto de todas las entradas posibles. Es decir, el dominio es el conjunto de todos los números reales posibles\(x\) para los que se puede determinar una salida de número real.

Esto está estrechamente relacionado con la ecuación\(f = x^2 sin x\). Con esta ecuación, frecuentemente pensamos en\(x\) como la entrada y\(y\) como la salida. De hecho, a veces escribimos\(y = f(x)\). La clave para recordar es que una función debe tener exactamente una salida por cada entrada. Cuando escribimos una ecuación como

\(y = \dfrac{1}{2} x^3 - 1,\)

podemos usar esta ecuación para definir\(y\) como una función de\(x\). Esto se debe a que cuando sustituimos un número real por\(x\) (la entrada), la ecuación produce exactamente un número real para\(y\) (la salida). Podemos darle un nombre a esta función, como\(g\), y escribir

\(y = g(x) = \dfrac{1}{2} x^3 - 1.\)

Sin embargo, tal como está escrito, una ecuación como

\(y^2 = x + 3\)

no se puede utilizar para definir\(y\) como una función de\(x\) ya que hay números reales que pueden ser sustituidos por\(x\) eso producirán más de un posible valor de\(y\). Por ejemplo, si\(x = 1\), entonces\(y^2 = 4\), y\(y\) podría ser -2 o 2.

¿Cuál de las siguientes ecuaciones se puede utilizar para definir una función con\(x \in \mathbb{R}\) como entrada y\(y \in \mathbb{R}\) como salida?

1. \(y = x^2 - 2\)
2. \(y^2 = x + 3\)
3. \(y = \dfrac{1}{2} x^3 - 1\)
4. \(y = \dfrac{1}{2} x sin x\)
5. \(x^2 + y^2 = 4\)
6. \(y = 2x - 1\)
7. \(y =dfrac{x}{x - 1}\)

Vista previa de la Actividad 2 (Algunos Otros Tipos de Funciones)

El dominio y codominio de las funciones en Preview Activity\(\PageIndex{1}\) es el conjunto\(\mathbb{R}\) de todos los números reales, o algún subconjunto de\(\mathbb{R}\). En la mayoría de estos casos, la forma en que la función asocia elementos del dominio con elementos del codominio es por una regla determinada por alguna expresión matemática. Por ejemplo, cuando decimos que esa\(f\) es la función tal que

\(f(x) = \dfrac{x}{x - 1},\)

entonces la regla algebraica que determina la salida de la función\(f\) cuando la entrada es\(x\) es\(\dfrac{x}{x - 1}\). En este caso, diríamos que el dominio de\(f\) es el conjunto de todos los números reales no iguales a 1 ya que la división por cero no está definida.

Sin embargo, el concepto de una función es mucho más general que esto. El dominio y el codominio de una función pueden ser cualquier conjunto, y la forma en que una función asocia elementos del dominio con elementos del codominio puede tener muchas formas diferentes. La regla de entrada-salida para una función puede ser una fórmula, una gráfica, una tabla, un proceso aleatorio o una descripción verbal. Exploraremos dos ejemplos diferentes en esta actividad previa.

1. \(b\)Sea la función que le asigne a cada persona su cumpleaños (mes y día). El dominio de la función\(b\) es el conjunto de todas las personas y el codominio de\(b\) es el conjunto de todos los días en un año bisiesto (es decir, del 1 de enero al 31 de diciembre, incluido el 29 de febrero).
   
   (a) Explicar por qué\(b\) realmente es una función. Llamaremos a esto la función de cumpleaños.
   (b) En 1995, Andrew Wiles se hizo famoso por publicar una prueba del último teorema de Fermat. (Véase A. D. Aczel, Fermat's Last Theorema: Unlocking the Secret of an Ancient Mathematical Problem, Dell Publishing, Nueva York, 1996.) El cumpleaños de Andrew Wiles es el 11 de abril de 1953. Traducir este hecho en notación funcional usando la “función cumpleaños”\(b\). Es decir, rellenar los espacios para los siguientes signos de interrogación:\[b(?) = ?.\]
   c) ¿Es verdadera o falsa la siguiente afirmación? Explique.
   Por cada día\(D\) del año, existe una persona\(x\) tal que\(b(x) = D\).
   d) ¿Es verdadera o falsa la siguiente afirmación? Explique.
   Para cualquier gente\(x\) y\(y\), si\(x\) y\(y\) son personas diferentes, entonces\(b(x) \ne b(y)\).
2. \(s\)Sea la función que asocia con cada número natural la suma de sus distintos divisores de números naturales. A esto se le llama la suma de la función de divisores. Por ejemplo, los divisores numéricos naturales de 6 son 1, 2, 3 y 6, y así
   \[\begin{array} {rcl} {s(6)} &= & {1 + 2 + 3 + 6} \\ {} &= & {12.} \end{array}\]
   
   (a) Calcular\(s(k)\) para cada número natural\(k\) del 1 al 15.
   b) ¿Existe un número natural\(n\) tal que\(s(n) = 5\)? Justifica tu conclusión.
   c) ¿Es posible encontrar dos números naturales diferentes\(m\) y\(n\) tales que\(s(m) = s(n)\)? Explique.
   (d) Utilice sus respuestas en (b) y (c) para determinar si las siguientes afirmaciones son verdaderas o falsas.
   i. Para cada uno\(m \in \mathbb{N}\), existe un número natural\(n\) tal que\(s(n) = m\).
   ii. Para todos\(m, n \in \mathbb{N}\), si\(m \ne n\), entonces\(s(m) \ne s(n)\).

La definición de una función

El concepto de una función es mucho más general que la idea de una función utilizada en cálculo o precálculo. En particular, el dominio y el codominio no tienen que ser subconjuntos de\(\mathbb{R}\). Además, la forma en que una función asocia elementos del dominio con elementos del codominio puede tener muchas formas diferentes. Esta regla de entrada-salida puede ser una fórmula, un gráfico, una tabla, un proceso aleatorio, un algoritmo informático o una descripción verbal. Dos de estos ejemplos se introdujeron en Actividad previa\(\PageIndex{2}\).

Para la función de cumpleaños, el dominio sería el conjunto de todas las personas y el codominio sería el conjunto de todos los días en un año bisiesto. Para la suma de la función de divisores, el dominio es el conjunto\(\mathbb{N}\) de números naturales, y el codominio también podría serlo\(\mathbb{N}\). En ambos casos, la regla input-output fue una descripción verbal de cómo asignar un elemento del codominio a un elemento del dominio.

Formalmente definimos el concepto de una función de la siguiente manera:

Definición

Una función de un conjunto\(A\) a un conjunto\(B\) es una regla que asocia con cada elemento\(x\) del conjunto\(A\) exactamente un elemento del conjunto\(B\). Una función de\(A\) a también\(B\) se llama mapeo de\(A\) a\(B\).

Notación de funciones. Cuando trabajamos con una función, usualmente le damos un nombre. El nombre suele ser una sola letra, como\(f\) o\(g\). Si\(f\) es una función del conjunto\(A\) para ser el conjunto\(B\), vamos a escribir\(f: A \to B\). Esto es simplemente una notación abreviada para el hecho de que\(f\) es una función del conjunto\(A\) al conjunto\(B\). En este caso, también decimos que los\(f\) mapas\(A\) a\(B\).

Definición

Vamos\(f: A \to B\). (Esto se lee, “Dejemos\(f\) ser una función de\(A\) a\(B\).”) El conjunto\(A\) se llama el dominio de la función\(f\), y escribimos\(A = dom(f)\). El conjunto\(B\) se llama el codominio de la función\(f\), y escribimos\(B = codom(f)\).

Si\(a \in A\), entonces el elemento de\(B\) que se asocia con\(a\) se denota por\(f(a)\) y se llama la imagen de un bajo\(f\). Si\(f(a) = b\), con\(b \in B\), entonces a se llama una preimagen de\(b\) debajo\(f\).

Alguna Terminología Funcional con un Ejemplo. Cuando tenemos una función\(f: A \to B\), a menudo escribimos\(y = f(x)\). En este caso, consideramos\(x\) que es un objeto no especificado que se puede elegir del conjunto\(A\), y diríamos que\(x\) es la variable independiente de la función\(f\) y\(y\) es la variable dependiente de la función\(f\).

Para un ejemplo específico, considere la función\(g: \mathbb{R} \to \mathbb{R}\), donde\(g(x)\) se define por la fórmula

\(g(x) = x^2 - 2.\)

Tenga en cuenta que esta es de hecho una función ya que dada cualquier entrada\(x\) en el dominio\(\mathbb{R}\),, hay exactamente una salida\(g(x)\) en el codominio,\(\mathbb{R}\). Por ejemplo,

\[\begin{array} {rcl} {g(-2)} &= & {(-2)^2 - 2 = 2,} \\ {g(5)} &= & {5^2 - 2 = 23,} \\ {g(\sqrt 2)} &= & {(\sqrt 2)^2 - 2 = 0,} \\ {g(-\sqrt 2)} &= & {(-\sqrt 2)^2 - 2 = 0.} \end{array}\]

Entonces decimos que la imagen de -2 debajo\(g\) es 2, la imagen de 5 debajo\(g\) es 23, y así sucesivamente.

Observe en este caso que el número 0 en el codominio tiene dos preimágenes,\(-\sqrt 2\) y\(\sqrt 2\). Esto no viola la definición matemática de una función ya que la definición sólo establece que cada entrada debe producir una y sólo una salida. Es decir, cada elemento del dominio tiene exactamente una imagen en el codominio. En ninguna parte la definición estipula que dos entradas diferentes deben producir diferentes salidas.

Encontrar las preimágenes de un elemento en el codominio a veces puede ser difícil. En general, si\(y\) está en el codominio, para encontrar sus preimágenes, hay que preguntar: “¿Para qué valores de\(x\) en el dominio vamos a tener\(y = g(x)\)?” Por ejemplo, para la función g, para encontrar las preimágenes de 5, necesitamos encontrar todas\(x\) para las cuales\(g(x) = 5\). En este caso, ya que\(g(x) = x^2 - 2\), podemos hacer esto resolviendo la ecuación

\(x^2 - 2 = 5.\)

Las soluciones de esta ecuación son\(-\sqrt 7\) y\(\sqrt 7\). Entonces para la función\(g\), las preimágenes de 5 son\(-\sqrt 7\) y\(\sqrt 7\). A menudo usamos notación set para esto y decimos que el conjunto de preimágenes de 5 para la función\(g\) es {\(-\sqrt 7\),\(\sqrt 7\)}.

También observe que para esta función, no todos los elementos del codominio tienen una preimagen. Por ejemplo, no hay entrada\(x\) tal que\(g(x) = -3\). Esto es cierto ya que para todos los números reales\(x\),\(x^2 \ge 0\) y por lo tanto\(x^2 - 2 \ge -2\). Esto significa que para todos\(x\) en\(\mathbb{R}\),\(g(x) \ge -2\).

Por último, tenga en cuenta que introducimos la función g con la frase, “Consideremos la función\(g: \mathbb{R} \to \mathbb{R}\), donde\(g(x)\) se define por la fórmula”\(g(x) = x^2 - 2\). Esta es una forma correcta de hacerlo, pero con frecuencia acortaremos esto a, “Dejemos que\(g: \mathbb{R} \to \mathbb{R}\) se definan por\(g(x) = x^2 - 2\)”, o “Vamos\(g: \mathbb{R} \to \mathbb{R}\), dónde”\(g(x) = x^2 - 2\).

Comprobación de progreso 6.1 (Imágenes y Preimágenes)

Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = x^2 - 5x\) para todos\(x \in \mathbb{R}\). y dejar\(g: \mathbb{Z} \to \mathbb{Z}\) ser definido por\(g(m) = m^2 - 5m\) para todos\(m \in \mathbb{Z}\).

1. Determinar\(f(-3)\) y\(f(\sqrt 8)\).
2. Determinar\(g(2)\) y\(g(-2)\).
3. Determinar el conjunto de toda la preimagen de 6 para la función\(f\).
4. Determinar el conjunto de toda la preimagen de 6 para la función\(g\).
5. Determinar el conjunto de toda la preimagen de 2 para la función\(f\).
6. Determinar el conjunto de toda la preimagen de 2 para la función\(g\).

Contestar

Agrega textos aquí. No elimine primero este texto.

El codominio y el rango de una función

Además del dominio y el codominio, hay otro conjunto importante asociado a una función. La necesidad de ello se ilustró en el ejemplo de la función de la\(g\) página 285. Para esta función, se notó que hay elementos en el codominio que no tienen preimagen o, equivalentemente, hay elementos en el codominio que no son la imagen de ningún elemento en el dominio. El conjunto del que estamos hablando es el subconjunto del codominio que consiste en todas las imágenes de los elementos del dominio de la función, y se llama el rango de la función.

Definición

Vamos\(f: A \to B\). El conjunto\(\{f(x)\ |\ x \in A\}\) se llama el rango de la función\(f\) y se denota por range (\(f\)). El rango de a veces\(f\) se llama la imagen de la función\(f\) (o la imagen de\(A\) debajo\(f\)).

El rango de\(f: A \to B\) podría definirse de manera equivalente de la siguiente manera:

rango (\(f\))\( = \{y \in B\ |\ y = f(x) \text{ for some } x \in A\}\).

Observe que esto significa que range (\(f\))\(\subseteq\) codom (\(f\)) pero no necesariamente significa ese range (\(f\))\(=\) codom (\(f\)). Que tengamos este conjunto de igualdad o no depende de la función\(f\). Se explorará más sobre esto en la Sección 6.3.

Comprobación de progreso 6.2 (codominio y rango)

1. \(b\)Sea la función que le asigne a cada persona su cumpleaños (mes y día).
   
   a) ¿Cuál es el dominio de esta función?
   (b) ¿Qué es un codominio para esta función?
   (c) En Actividad Previa\(\PageIndex{2}\), determinamos que la siguiente afirmación es cierta: Por cada día\(D\) del año, existe una persona\(x\) tal que\(b(x) = D\). ¿Qué nos dice esto sobre el rango de la función\(b\)? Explique.
2. \(s\)Sea la función que asocia con cada número natural la suma de sus distintos factores numéricos naturales.
   
   a) ¿Cuál es el dominio de esta función?
   (b) ¿Qué es un codominio para esta función?
   (c) En Preview Activity\(\PageIndex{2}\), determinamos que la siguiente afirmación es falsa:
   Para cada uno\(m \in \mathbb{N}\), existe un número natural\(n\) tal que\(s(n) = m\).
   Dar un ejemplo de un número natural\(m\) que demuestre que esta afirmación es falsa, y explicar lo que esto nos dice sobre el rango de la función\(s\).

Contestar

Agrega textos aquí. No elimine primero este texto.

La Gráfica de una Función Real

Terminaremos esta sección con métodos para comunicar visualmente información sobre dos tipos específicos de funciones. El primero es el método familiar de graficar funciones que fue una parte importante de algunos cursos previos de matemáticas. Por ejemplo, considere la función\(g: \mathbb{R} \to \mathbb{R}\) definida por\(g(x) = x^2 - 2x - 1\).

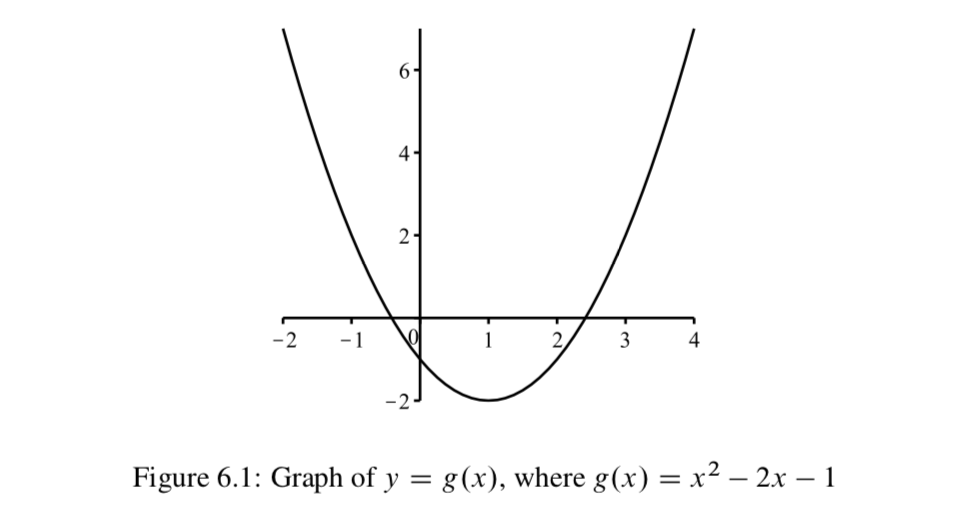
Cada punto de esta gráfica corresponde a un par ordenado (\(x\),\(y\)) de números reales, donde\(y = g(x) = x^2 - 2x - 1\). Debido a que usamos el plano cartesiano al dibujar este tipo de gráfica, solo podemos usar este tipo de gráfica cuando tanto el dominio como el codominio de la función son subconjuntos de los números reales\(\mathbb{R}\). Tal función a veces se llama una función real. La gráfica de una función real es una forma visual de comunicar información sobre la función. Por ejemplo, el rango de\(g\) es el conjunto de todos los valores y que corresponden a puntos en la gráfica. En este caso, la gráfica de\(g\) es una parábola y tiene un vértice en el punto (1, -2). (Nota: La coordenada x del vértice se puede encontrar usando cálculo y resolviendo la ecuación\(f\prime (x) = 0\).) Dado que la gráfica de la función\(g\) es una parábola, sabemos que el patrón que se muestra en el extremo izquierdo y el extremo derecho de la gráfica continúa y podemos concluir que el rango de\(g\) es el conjunto de todos\(y \in \mathbb{R}\) tales que\(y \ge -2\). Es decir,

rango (\(g\))\( = \{y \in \mathbb{R}\ |\ y \ge -2\}.\)

Comprobación de progreso 6.3 (Uso de la Gráfica de una Función Real)

La gráfica de la Figura 6.2 muestra la gráfica de (ligeramente más de) dos periodos completos para una función\(f: \mathbb{R} \to \mathbb{R}\), donde\(f(x) = Asin(Bx)\) para algunas constantes positivas de número real\(A\) y\(B\).

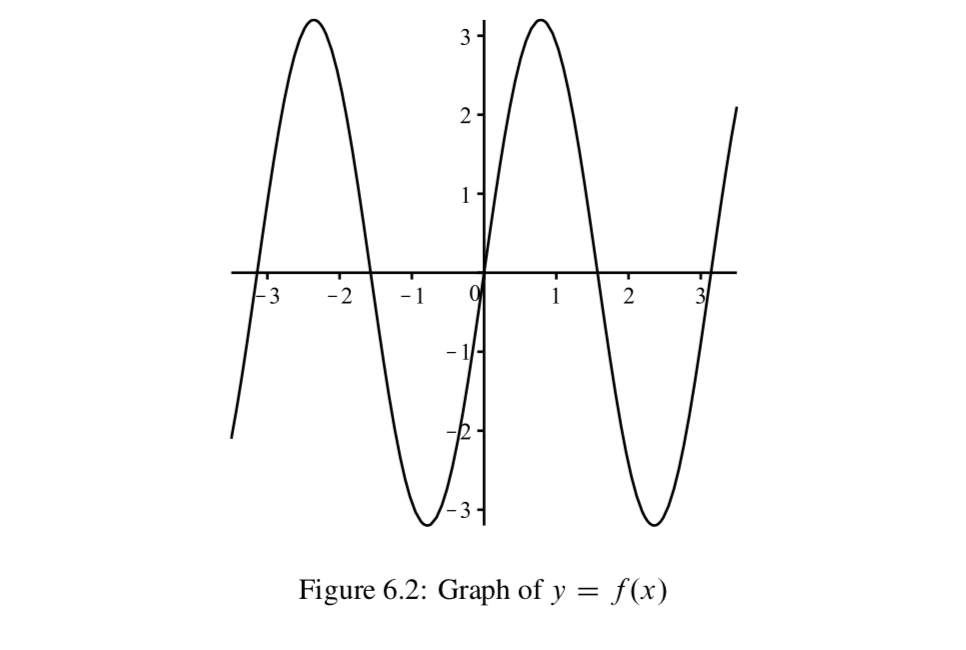
1. Podemos usar la gráfica para estimar la salida de varias entradas. Esto se hace estimando la\(y\) coordenada -para el punto en la gráfica con una\(x\) coordenada -especificada. En la gráfica, dibuje líneas verticales en\(x = -1\) y\(x = 2\) y estime los valores de\(f(-1)\) y\(f(2)\).
2. Del mismo modo, podemos estimar entradas de la función que producen una salida especificada. Esto se hace estimando las\(x\) -coordenadas de los puntos en la gráfica que tienen una\(y\) coordenada especificada. Dibuje una línea horizontal en\(y = 2\) y estime al menos dos valores de\(x\) tal que\(f(x) = 2\).
3. Utilice la gráfica Figura 6.2 para estimar el rango de la función\(f\).

Contestar

Agrega textos aquí. No elimine primero este texto.

Diagramas de flecha

A veces el dominio y el codominio de una función son conjuntos pequeños y finitos. Cuando este es el caso, podemos definir una función simplemente especificando las salidas para cada entrada en el dominio. Por ejemplo, si dejamos\(A = \{1, 2, 3\}\) y dejamos\(B = \{a, b\}\), podemos definir una función\(F: A \to B\) especificando que

\(F(1) = a, F(2) = a,\text{ and } F(3) = b.\)

Esta es una función ya que cada elemento del dominio está mapeado a exactamente un elemento en\(B\). Una manera conveniente de ilustrar o visualizar este tipo de función es con un llamado diagrama de flechas como se muestra en la Figura 6.3. Un diagrama de flecha puede

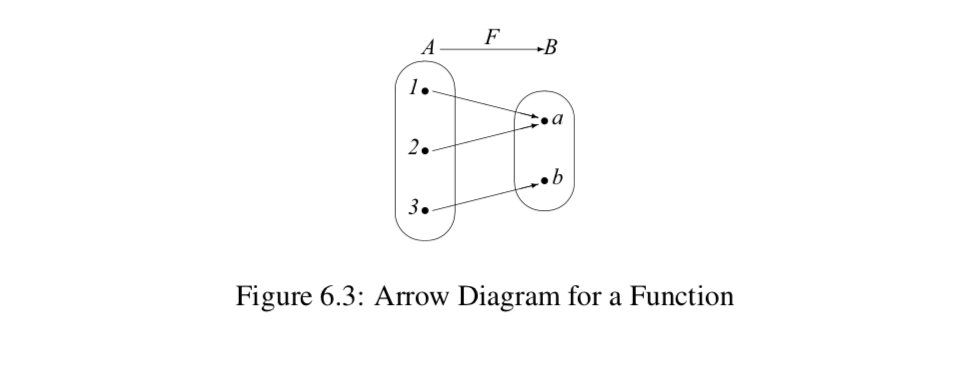
ser usado cuando el dominio y el codominio de la función son finitos (y pequeños). Representamos los elementos de cada conjunto con puntos y luego usamos flechas para mostrar cómo se asocian los elementos del dominio con elementos del codominio. Por ejemplo, la flecha desde el punto 2\(A\) hasta el punto\(a\) en\(B\) representa el hecho de que\(F(2) = a\). En este caso, podemos usar el diagrama de flechas en la Figura 6.3 para concluir ese rango (\(F\))\( = \{a, b\}\).

Comprobación de progreso 6.4 (Trabajo con diagramas de flecha)

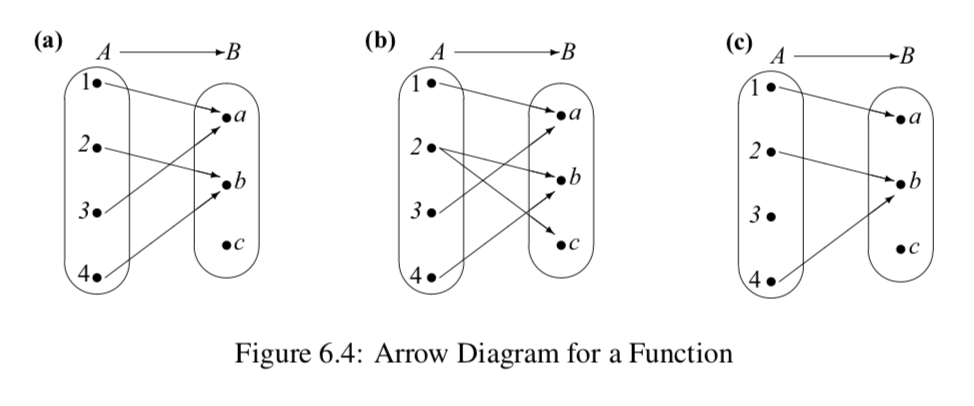
Dejar\(A = \{1, 2, 3, 4\}\) y dejar\(B = \{a, b, c\}\).

1. ¿Cuál de los diagramas de flecha en la Figura 6.4 se puede utilizar para representar una función de\(A\) a\(B\)? Explique.
2. Para aquellos diagramas de flecha que se pueden usar para representar una función de\(A\) a\(B\), determinar el rango de la función.
   

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicios 6.1

1. Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = x^2 - 2x\).
   
   (a) Evaluar\(f(-3)\),\(f(-1)\),\(f(1)\), y\(f(3)\).
   (b) Determinar el conjunto de todas las preimágenes de 0 y el conjunto de todas las preimágenes de 4.
   (c) Esbozar una gráfica de la función\(f\).
   d) Determinar el rango de la función\(f\).
2. Dejar\(\mathbb{R} ^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\), y dejar\(s: \mathbb{R} \to \mathbb{R} ^{\ast}\) ser definido por\(s(x) = x^2\).
   
   (a) Evaluar\(s(-3)\),\(s(-1)\),\(s(1)\), y\(s(3)\).
   (b) Determinar el conjunto de todas las preimágenes de 0 y el conjunto de todas las preimágenes de 2.
   (c) Esbozar una gráfica de la función\(s\).
   d) Determinar el rango de la función\(s\).
3. Dejar\(f: \mathbb{Z} \to \mathbb{Z}\) ser definido por\(f(m) = 3 - m\).
   
   (a) Evaluar\(f(-7)\),\(f(-3)\),\(f(3)\), y\(f(7)\).
   (b) Determinar el conjunto de todas las preimágenes de 5 y el conjunto de todas las preimágenes de 4.
   (c) Determinar el rango de la función\(f\).
   (d) Esta función puede considerarse una función real ya que\(\mathbb{Z} \subseteq \mathbb{R}\). Haga un boceto de una gráfica de esta función. Nota: La gráfica será un conjunto infinito de puntos que se encuentran en una línea. No obstante, no será una línea ya que su dominio no es\(\mathbb{R}\) sino lo es\(\mathbb{Z}\).
4. Dejar\(f: \mathbb{Z} \to \mathbb{Z}\) ser definido por\(f(m) = 2m + 1\).
   
   (a) Evaluar\(f(-7)\),\(f(-3)\),\(f(3)\), y\(f(7)\).
   (b) Determinar el conjunto de todas las preimágenes de 5 y el conjunto de todas las preimágenes de 4.
   (c) Determinar el rango de la función\(f\).
   (d) Esbozar una gráfica de la función\(f\). Ver los comentarios en Ejercicio (3d).
5. Recordemos que una función real es una función cuyo dominio y codominio son subconjuntos de los números reales R. (Ver página 288.) La mayoría de las funciones utilizadas en el cálculo son funciones reales. Muy a menudo, una función real viene dada por una fórmula o una gráfica sin referencia específica al dominio o al codominio. En estos casos, la convención habitual es suponer que el dominio de la función real\(f\) es el conjunto de todos los números reales\(x\) para los que\(f(x)\) es un número real, y que el codominio es\(\mathbb{R}\). Por ejemplo, si definimos la función (real)\(f\) por
   \[f(x) = \dfrac{x}{x - 2},\]
   estaríamos asumiendo que el dominio es el conjunto de todos los números reales que no son iguales a 2 y que el codominio en\(\mathbb{R}\).
   Determinar el dominio y rango de cada una de las siguientes funciones reales. Podría ser útil usar una calculadora gráfica para trazar una gráfica de la función.
   
   a) La función\(k\) definida por\(k(x) = \sqrt{x - 3}\)
   (b) La función\(F\) definida por\(F(x) = ln(2x - 1)\)
   (c) La función definida por (d) La función\(f\) definida por\(f(x) = 3sin(2x)\)
   (d) La función\(g\) definida por \(g(x) = \dfrac{4}{x^2 - 4}\)
   e) La función\(G\) definida por\(G(x) = 4cos(\pi x) + 8\)
6. El número de divisores funciona. \(d\)Sea la función que asocia con cada número natural el número de sus divisores numéricos naturales. Ahí es\(d: \mathbb{N} \to \mathbb{N}\) donde\(d(n)\) está el número de divisores numéricos naturales de\(n\). Por ejemplo,\(d(6) = 4\) ya que 1, 2, 3 y 6 son los divisores numéricos naturales de 6.
   
   a) Calcular\(d(k)\) para cada número natural\(k\) del 1 al 12.
   b) ¿Existe un número natural\(n\) tal que\(d(n) = 1\)? Cuál es el conjunto de preimágenes del número natural 1.
   c) ¿Existe un número natural\(n\) tal que\(d(n) = 2\)? Si es así, determinar el conjunto de todas las preimágenes del número natural 2.
   d) ¿Es verdadera o falsa la siguiente afirmación? Justifica tu conclusión.
   Para todos\(m, n \in \mathbb{N}\), si\(m \ne n\), entonces\(d(m) \ne d(n)\).
   e) Calcular\(d(2^k)\) para\(k = 0\) y para cada número natural\(k\) del 1 al 6.
   (f) Con base en su trabajo en el Ejercicio (6e), haga una conjetura para una fórmula para\(d(2^n)\) donde\(n\) es un entero no negativo. Entonces explica por qué tu conjetura es correcta.
   g) ¿Es verdadera o falsa la siguiente afirmación?
   Para cada uno\(n \in \mathbb{N}\), existe un número natural\(m\) tal que\(d(m) = n\).
7. En el Ejercicio (6), se introdujo la función de número de divisores\(d\). Para esta función,\(d: \mathbb{N} \to \mathbb{N}\), donde\(d(n)\) está el número de divisores numéricos naturales de\(n\).
   Una función que está relacionada con esta función es la llamada función de conjunto de divisores. Esto puede definirse como una función\(S\) que asocia con cada número natural el conjunto de sus distintos factores numéricos naturales. Por ejemplo,\(S(6) = \{1, 2, 3, 6\}\) y\(S(10) = \{1, 2, 5, 10\}\).
   
   (a) Discutir la función\(S\) exponiendo cuidadosamente su dominio, codominio y su regla para determinar los resultados.
   (b) Determinar\(S(n)\) para al menos cinco valores diferentes de\(n\).
   (c) Determinar\(S(n)\) para al menos tres valores diferentes de números primos de\(n\).
   d) ¿Existe un número natural\(n\) tal que la tarjeta (\(S(n) = 1\))? Explique. [Recordemos que card (\(S(n)\)) es el número de elementos en el conjunto\(S(n)\).]
   e) ¿Existe un número natural\(n\) tal que la tarjeta (\(S(n) = 2\))? Explique.
   (f) Escribir la salida de la función\(d\) en términos de la salida de la función\(S\). Es decir, escribir\(d(n)\) en términos de\(S(n)\).
   g) ¿Es verdadera o falsa la siguiente afirmación? Justifica tu conclusión.
   Para todos los números naturales\(m\) y\(n\), si\(m \ne n\), entonces\(S(m) \ne S(n)\).
   h) ¿Es verdadera o falsa la siguiente afirmación? Justifica tu conclusión.
   Para todos los conjuntos\(T\) que son subconjuntos de\(\mathbb{N}\), existe un número natural\(n\) tal que\(S(n) = T\).
   
   Exploraciones y actividades
8. Creación de Funciones con Dominios Finitos. Vamos\(A = \{a, b, c, d\}\),\(B= \{a, b, c\}\). y\(C = \{s, t, u, v\}\). En cada uno de los siguientes ejercicios, dibuja un diagrama de flechas para representar tu función cuando sea apropiado.
   
   (a) Crear una función\(f: A \to C\) cuyo rango sea el conjunto\(C\) o explicar por qué no es posible construir tal función.
   (b) Crear una función\(f: A \to C\) cuyo rango sea el conjunto\(\{u,v\}\) o explicar por qué no es posible construir tal función.
   (c) Crear una función\(f: B \to C\) cuyo rango sea el conjunto\(C\) o explicar por qué no es posible construir tal función.
   (d) Crear una función\(f: A \to C\) cuyo rango sea el conjunto\(\{u\}\) o explicar por qué no es posible construir tal función.
   (e) De ser posible, crear una función\(f: A \to C\) que satisfaga la siguiente condición:
   Para todos\(x,y \in A\), si\(x \ne y\), entonces\(f(x) \ne f(y)\).
   Si no es posible crear tal función, explique por qué.
   f) De ser posible, crear una función\(f: A \to \{s, t, u\}\) que satisfaga la siguiente condición:
   Para todos\(x,y \in A\), si\(x \ne y\), entonces\(f(x) \ne f(y)\).
   Si no es posible crear tal función, explique por qué.

Contestar

Agrega textos aquí. No elimine primero este texto.