9.2: Conjuntos Contables

Vista previa de la actividad\(\PageIndex{1}\): Introduction to Infinite Sets

En la Sección 9.1, definimos un conjunto finito para ser el conjunto vacío o un conjunto\(A\) tal que\(A \thickapprox \mathbb{N}_k\) para algún número natural\(k\). También definimos un conjunto infinito para ser un conjunto que no es finito, pero la pregunta ahora es: “¿Cómo sabemos si un conjunto es infinito?” Una forma de determinar si un conjunto es un conjunto infinito es usar Corolario 9.8, que establece que un conjunto finito no es equivalente a ninguno de sus subconjuntos. Podemos escribir esto como una declaración condicional de la siguiente manera:

Si\(A\) es un conjunto finito, entonces no\(A\) es equivalente a ninguno de sus subconjuntos propios. o más formalmente como

Para cada conjunto\(A\), si\(A\) es un conjunto finito, entonces para cada subconjunto apropiado\(B\) de\(A\),\(A \not\thickapprox B\).

1. Escribir el contrapositivo de la sentencia condicional anterior. Luego explique cómo se puede usar esta afirmación para determinar si un conjunto es infinito.
2. Deje que DC sea el conjunto de todos los números naturales impares. En Actividad Previa\(\PageIndex{1}\) de la Sección 9.1, lo demostramos\(\mathbb{N} \thickapprox D^{+}\).

   (a) Utilice esto para explicar cuidadosamente por qué\(\mathbb{N}\) es un conjunto infinito.
   (b) ¿Es\(D^{+}\) un conjunto finito o un conjunto infinito? Explique cuidadosamente cómo sabe.

3. \(b\)Sea un número real positivo. Dejar (0, 1) y\((0, b)\) ser los intervalos abiertos de 0 a 1 y 0 a\(b\), respectivamente. En la Parte (3) de Avance Check 9.2 (en la página 454), lo probamos\((0, 1) \thickapprox (0, b)\).

   (a) Utilizar un valor para\(b\) dónde\(0 < b < 1\) explicar por qué (0, 1) es un conjunto infinito.
   (b) Utilizar un valor para\(b\) dónde\(b > 1\) explicar por qué\((0, b)\) es un conjunto infinito.

Vista previa de la actividad\(\PageIndex{2}\): A Function from \(\mathbb{N}\) to \(\mathbb{Z}\)

En esta actividad de vista previa, definiremos y exploraremos una función\(f: \mathbb{N} \to \mathbb{Z}\). Comenzaremos definiendo\(f(n)\) para los primeros números naturales\(n\).

Observe que si enumeramos las salidas de\(f\) en el orden\(f(1)\)\(f(2)\)\(f(3)\),,,..., creamos la siguiente lista de enteros: 0, 1, -1, 2, -2, 3, -3,... También podemos ilustrar los resultados de esta función con el siguiente diagrama:

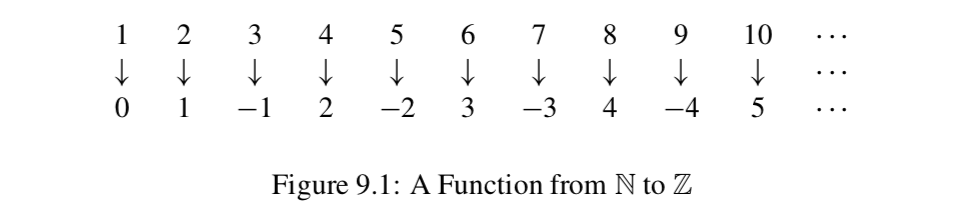
1. Si el patrón sugerido por los valores de función que hemos definido continúa, ¿qué son\(f(11)\) y\(f(12)\)? ¿\(f(n)\)Para qué\(n\) sirve del 13 al 16?
2. Si el patrón de salidas continúa, ¿la función\(f\) parece ser una inyección? ¿\(f\)Parece ser una sobrejección? (No se requieren pruebas formales).
   
   Ahora intentaremos determinar una fórmula para\(f(n)\), dónde\(n \in \mathbb{N}\). En realidad determinaremos dos fórmulas: una para cuándo\(n\) es par y otra para cuándo\(n\) es impar.
3. Mira el patrón de los valores de\(f(n)\) cuando\(n\) es par. ¿Qué parece ser una fórmula para\(f(n)\) cuando\(n\) es par?
4. Mira el patrón de los valores de\(f(n)\) cuando n es impar. ¿Qué parece ser una fórmula para\(f(n)\) cuando\(n\) es extraño?
5. Utilice la obra de la Parte (3) y la Parte (4) para completar lo siguiente: Definir\(f: \mathbb{N} \to \mathbb{Z}\), donde
   \[f(n) = \begin{cases} ?? & \text{ if \(n\) is even} \\ ?? & \text{ if \(n\) is odd.} \end{cases}\]
6. Utilice la fórmula de la Parte (5) para (a) Calcular\(f(1)\) a través\(f(10)\). ¿Estos resultados son consistentes con el patrón exhibido al inicio de esta actividad previa?
   b) Calcular\(f(1000)\) y\(f(1001)\).
   (c) Determinar el valor de\(n\) para que\(f(n) = 1000\).

En esta sección, describiremos varios conjuntos infinitos y definiremos el número cardinal para los llamados conjuntos contables. La mayoría de nuestros ejemplos serán subconjuntos de algunos de nuestros sistemas de números estándar como\(\mathbb{N}\),\(\mathbb{Z}\), y\(\mathbb{Q}\).

Conjuntos Infinitos

En Preview Activity\(\PageIndex{1}\), vimos cómo usar el Corolario 9.8 para demostrar que un conjunto es infinito. Este corolario implica que si A es un conjunto finito, entonces A no es equivalente a ninguno de sus subconjuntos propios. Al escribir el contrapositivo de esta declaración condicional, podemos reafirmar el Corolario 9.8 en la siguiente forma:

Corolario 9.8

Si un conjunto\(A\) es equivalente a uno de sus subconjuntos propios, entonces\(A\) es infinito.

En Actividad previa\(\PageIndex{1}\), utilizamos Corolario 9.8 para demostrar que

• El conjunto de números naturales,\(\mathbb{N}\), es un conjunto infinito.
• El intervalo abierto (0, 1) es un conjunto infinito.

Si bien el Corolario 9.8 proporciona una manera de demostrar que un conjunto es infinito, a veces es más conveniente usar una prueba por contradicción para demostrar que un conjunto es infinito. La idea es utilizar los resultados de la Sección 9.1 sobre conjuntos finitos para ayudar a obtener una contradedicción. Esto se ilustra en el siguiente teorema.

Teorema 9.10.

Dejar\(A\) y\(B\) ser conjuntos.

1. Si\(A\) es infinito y\(A \thickapprox B\), entonces\(B\) es infinito.
2. Si\(A\) es infinito y\(A \subseteq B\), entonces\(B\) es infinito.

Prueba

Demostraremos la parte (1). El comprobante de la parte (2) es ejercicio (3) en la página 473.

Para probar la parte (1), utilizamos una prueba por contradicción y asumimos que A es un conjunto infinito,\(A \thickapprox B\), y no\(B\) es infinito. Es decir,\(B\) es un conjunto finito. Dado que\(A \thickapprox B\) y\(B\) es finito, el Teorema 9.3 en la página 455 implica que\(A\) es un conjunto finito. Esto es una contradicción a la suposición que\(A\) es infinita. Por lo tanto, hemos demostrado que si\(A\) es infinito y\(A \thickapprox B\), entonces\(B\) es infinito.

Comprobación de progreso 9.11 (Ejemplos de conjuntos infinitos)

1. En Preview Activity\(\PageIndex{1}\), usamos Corolario 9.8 para demostrar que\(\mathbb{N}\) es un conjunto infinito. Ahora usa esto y el Teorema 9.10 para explicar por qué nuestros sistemas numéricos estándar (\(\mathbb{Z}\),\(\mathbb{Q}\), y\(\mathbb{R}\)) son conjuntos infinitos. También, explique por qué el conjunto de todos los números racionales positivos\(\mathbb{Q}^{+}\), y el conjunto de todos los números reales positivos,\(\mathbb{R}^{+}\), son conjuntos infinitos.
2. Dejar\(D^{+}\) ser el conjunto de todos los números naturales impares. En la Parte (2) de Actividad Previa\(\PageIndex{1}\), lo demostramos\(D^{+} \thickapprox \mathbb{N}\). Usa el Teorema 9.10 para explicar por qué\(D^{+}\) es un conjunto infinito.
3. Demostrar que el conjunto\(E^{+}\) de todos los números naturales pares es un conjunto infinito.

Responder

Agrega textos aquí. No elimine primero este texto.

Conjuntos infinitos contables

En la Sección 9.1, se utilizó el conjunto\(\mathbb{N}_k\) como conjunto estándar con cardinalidad\(k\) en el sentido de que un conjunto es finito si y sólo si es equivalente a\(\mathbb{N}_k\). De manera similar, utilizaremos algunos conjuntos infinitos como conjuntos estándar para ciertos números cardinales infinitos. El primer set que usaremos es\(\mathbb{N}\).

Vamos a definir formalmente lo que significa decir que los elementos de un conjunto pueden ser “contados” usando los números naturales. Los elementos de un conjunto finito se pueden “contar” definiendo una biyección (correspondencia uno a uno) entre el conjunto y\(\mathbb{N}_k\) para algún número natural\(k\). Podremos “contar” los elementos de un conjunto infinito si podemos definir una correspondencia uno a uno entre el conjunto y\(\mathbb{N}\).

Definición

La cardinalidad de\(\mathbb{N}\) se denota por\(\aleph_0\). El símbolo\(\aleph\) es la primera letra del alfabeto hebreo, aleph. El subíndice 0 a menudo se lee como “nada” (o a veces como “cero” o “nulo”). Así que escribimos

\(\text{card}(\mathbb{N}) = \aleph_0\)

y decir que la cardinalidad de\(\mathbb{N}\) es “aleph nada”.

Definición

Un conjunto\(A\) es contablemente infinito siempre y cuando eso\(A \thickapprox \mathbb{N}\). En este caso, escribimos

\(\text{card}(A) = \aleph_0\)

Un conjunto que es contablemente infinito a veces se denomina conjunto denumerable. Un conjunto es contable siempre que sea finito o contablemente infinito. Un conjunto infinito que no es infinitamente contable se llama conjunto incontable.

comprobación de progreso 9.12. (ejemplos de conjuntos infinitos contables)

1. En Vista previa\(\PageIndex{1}\) de la Actividad de la Sección 9.1, lo demostramos\(\mathbb{N} \thickapprox D^{+}\), donde\(D^{+}\) está el conjunto de todos los números naturales impares. Explique por qué\(\text{card}(D^{+}) = \aleph_0\).
2. Usa un resultado de la Comprobación de Progreso 9.11 para explicar por qué\(\text{card}(E^{+}) = \aleph_0\).
3. En este punto, si queremos demostrar que un conjunto\(S\) es contablemente infinito, debemos encontrar una biyección entre el conjunto\(S\) y algún conjunto que se sabe que es contablemente infinito.

   Deja\(S\) ser el conjunto de todos los números naturales que son cuadrados perfectos. Definir una función

   \[f: S \to \mathbb{N}\]
   que se puede utilizar para probar eso\(S \thickapprox \mathbb{N}\) y, por lo tanto, eso\(\text{card}(S) = \aleph_0\).

Responder

Agrega textos aquí. No elimine primero este texto.

El hecho de que el conjunto de enteros sea un conjunto contablemente infinito es lo suficientemente importante como para llamarse teorema. La función que utilizaremos para establecer que\(\mathbb{N} \thickapprox \mathbb{Z}\) fue explorada en Vista previa de Actividad\(\PageIndex{2}\).

Teorema 9.13

El conjunto\(\mathbb{Z}\) de números enteros es contablemente infinito, y así\(\text{card}(\mathbb{Z}) = \aleph_0\)

Prueba

Para probarlo\(\mathbb{N} \thickapprox \mathbb{Z}\), utilizaremos la siguiente función:\(f: \mathbb{N} \to \mathbb{Z}\), donde

\(f(n) = \begin{cases} \dfrac{n}{2} & \text{ if \(n\)es par}\\\ dfrac {1 - n} {2} &\ text {si\(n\) es impar.} \ end {casos}\)

De nuestro trabajo en Preview Activity\(\PageIndex{2}\), parece que si n es un número natural par, entonces\(f(n) > 0\), y si\(n\) es un número natural impar, entonces\(f(n) \le 0\). Por lo que parece razonable usar casos para probar que\(f\) es una sobreyección y eso\(f\) es una inyección. Para probar que eso\(f\) es una sobrejección, dejamos\(y \in \mathbb{Z}\).

• Si\(y > 0\), entonces\(2y \in \mathbb{N}\), y
  \[f(2y) = \dfrac{2y}{2} = y.\]
• Si\(y \le 0\), entonces\(-2y \ge 0\) y\(1 - 2y\) es un número natural impar. De ahí que,
  \[f(1-2y) = \dfrac{1 - (1 - 2y)}{2} = \dfrac{2y}{2} = y.\]

Estos dos casos prueban que si\(y \in \mathbb{Z}\), entonces existe\(n \in \mathbb{N}\) tal que\(f(n) = y\). De ahí,\(f\) es una sobrejección.

Para probar que\(f\) es una inyección, lo dejamos\(m, n \in \mathbb{N}\) y asumimos eso\(f(m) = f(n)\). Primero tenga en cuenta que si uno de\(m\) y\(n\) es impar y el otro es par, entonces uno de\(f(m)\) y\(f(n)\) es positivo y el otro es menor o igual a 0. Entonces si\(f(m) = f(n)\), entonces ambos\(m\) y\(n\) deben ser pares o ambos\(m\) y\(n\) deben ser impares.

• Si ambos\(m\) y\(n\) son parejos, entonces
  \[f(m) = f(n) \text{ implies that } \dfrac{m}{2} = \dfrac{n}{2}\]
  y de ahí eso\(m = n\).
• Si ambos\(m\) y\(n\) son impares, entonces A
  \[f(m) = f(n) \text{ implies that } \dfrac{1 - m}{2} = \dfrac{1 - n}{2}.\]
  partir de esto, concluimos eso\(1 - m = 1 - n\) y de ahí aquello\(m = n\). Esto demuestra que si\(f(m) = f(n)\), entonces\(m = n\) y de ahí eso\(f\) es una inyección.

Ya que\(f\) es tanto una sobreyección como una inyección, vemos que\(f\) es una biyección y, por lo tanto,\(\mathbb{N} \thickapprox \mathbb{Z}\). De ahí,\(\mathbb{Z}\) es contablemente infinito y\(\text{card}(\mathbb{Z}) = \aleph_0\).

El resultado en el Teorema 9.13 puede parecer un poco sorprendente. Exhibe una de las distinciones entre conjuntos finitos e infinitos. Si agregamos elementos a un conjunto finito, aumentaremos su tamaño en el sentido de que el nuevo conjunto tendrá una cardinalidad mayor que el conjunto anterior. Sin embargo, con conjuntos infinitos, podemos agregar elementos y el nuevo conjunto aún puede tener la misma cardinalidad que el conjunto original. Por ejemplo, existe una correspondencia uno a uno entre los elementos de los conjuntos\(\mathbb{N}\) y\(\mathbb{Z}\). Nosotros decimos que estos conjuntos tienen la misma cardinalidad.

A continuación se resumen algunos de los principales ejemplos que tratan de la cardinalidad de los conjuntos que hemos explorado.

• Los conjuntos\(\mathbb{N}_k\), donde\(k \in \mathbb{N}\), son ejemplos de conjuntos que son contables y finitos.
• Los conjuntos\(\mathbb{N}\)\(\mathbb{Z}\), el conjunto de todos los números naturales impares y el conjunto de todos los números naturales pares son ejemplos de conjuntos que son contables y contablemente infinitos.
• Aún no hemos probado que ningún conjunto sea incontable.

El conjunto de números racionales positivos

Si esperamos encontrar un conjunto incontable en nuestros sistemas numéricos habituales, los números racionales podrían ser el lugar para comenzar a buscar. Una de las principales diferencias entre el conjunto de números racionales y los enteros es que dado cualquier entero m, hay un número entero siguiente, a saber\(m + 1\). Esto no es cierto para el conjunto de números racionales. Sabemos que\(\mathbb{Q}\) se cierra bajo división (por números racionales distintos de cero) y veremos que esta propiedad implica que dados dos números racionales cualesquiera, también podemos encontrar un número racional entre ellos. De hecho, entre dos números racionales cualesquiera, podemos encontrar infinitamente muchos números racionales. Es esta propiedad la que nos puede llevar a creer que hay “más” números racionales que números enteros.

La idea básica será “ir a mitad de camino” entre dos números racionales. Por ejemplo, si usamos\(a = \dfrac{1}{3}\) y\(b = \dfrac{1}{2}\), podemos usar

\(\dfrac{a + b}{2} = \dfrac{1}{2} (\dfrac{1}{3} + \dfrac{1}{2}) = \dfrac{5}{12}\)

como un número racional entre\(a\) y\(b\). Entonces podemos repetir este proceso para encontrar un número racional entre\(\dfrac{5}{12}\) y\(\dfrac{1}{2}\).

Así que ahora vamos a dejar\(a\) y\(b\) ser cualesquiera dos números racionales con\(a < b\) y dejar\(c_1 = \dfrac{a + b}{2}\). Entonces vemos que

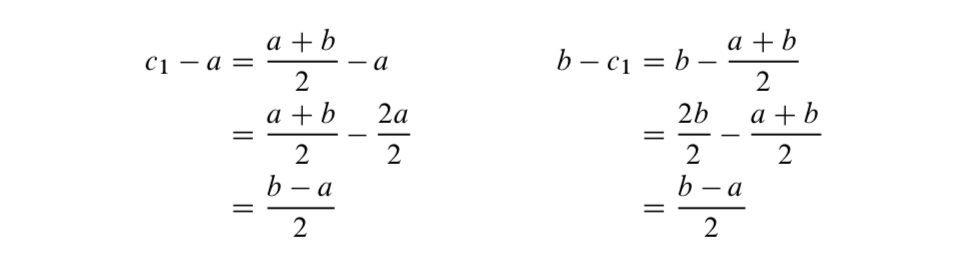
Ya que\(b > a\), vemos eso\(b - a > 0\) y así las ecuaciones anteriores muestran que\(c_1 - a > 0\) y\(b - c_1 > 0\). Entonces podemos concluir eso\(a < c_1 < b\).

Ahora podemos repetir este proceso utilizando\(c_2 = \dfrac{c_1 + b}{2}\) y demostrando que\(c_1 < c_2 < b\), de hecho, para cada número natural, podemos definir

\(c_{k + 1} = \dfrac{c_k + b}{2}\)

y obtener el resultado que\(a < c_1 < c_2 < \cdot\cdot\cdot < c_n < \cdot\cdot\cdot < b\) y esto demuestra que el conjunto\(\{c_k\ |\ k \in \mathbb{N}\) es un conjunto contablemente infinito donde cada elemento es un número racional entre\(a\) y\(b\). (Una prueba formal se puede completar mediante inducción matemática. Ver Ejercicio ().

Este resultado es cierto por muy cercanos que estén\(a\) y\(b\) estén. Por ejemplo, ahora podemos concluir que hay infinitamente muchos números racionales entre 0 y\(\dfrac{1}{10000}\) Esto podría sugerir que el conjunto\(\mathbb{Q}\) de números racionales es incontable. Sorprendentemente, este no es el caso. Comenzamos con una prueba de que el conjunto de números racionales positivos es contable.

Teorema 9.14

El conjunto de números racionales positivos es contablemente infinito.

Prueba

Podemos escribir todos los números racionales positivos en una matriz bidimensional como se muestra en la Figura 9.2. La fila superior de la Figura 9.2 representa el numerador del número racional, y la columna izquierda representa el denominador. Seguimos las flechas en la Figura 9.2 para definir\(f: \mathbb{N} \to \mathbb{Q}^{+}\). La idea es comenzar en la esquina superior izquierda de la mesa y pasar a diagonales sucesivas de la siguiente manera:

• Comenzamos con todas las fracciones en las que la suma del numerador y denominador es 2 (solo\(\dfrac{1}{1}\)). Entonces\(f(1) = \dfrac{1}{1}\).
  
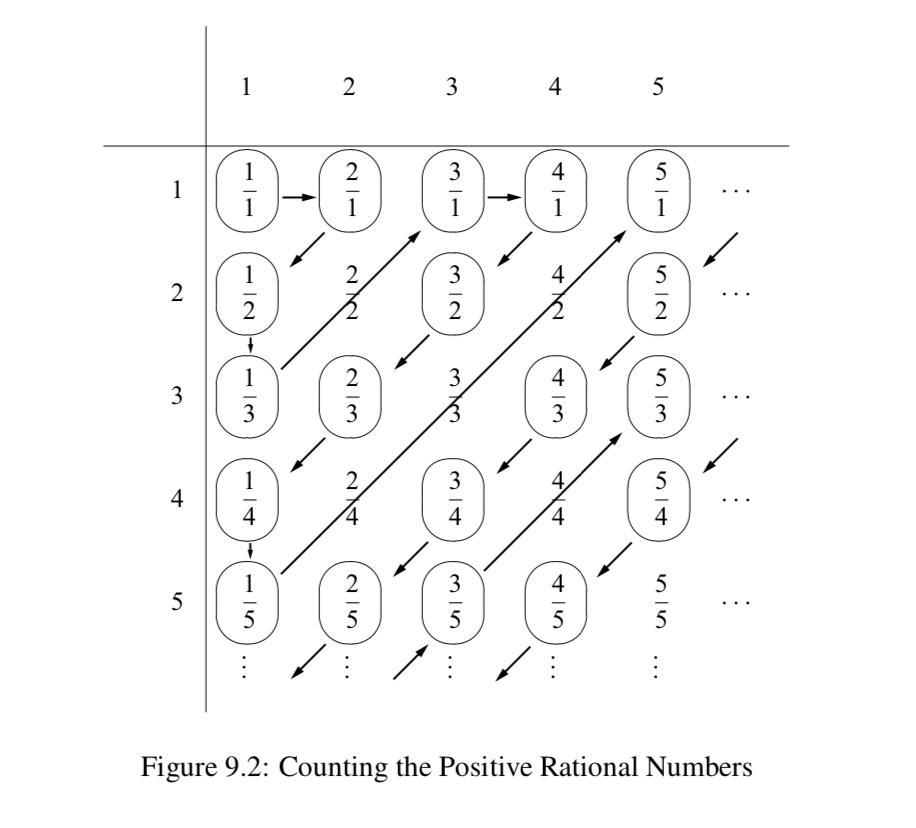
• A continuación usamos aquellas fracciones en las que la suma del numerador y denominador es 3. Entonces\(f(2) = \dfrac{2}{1}\) y\(f(3) = \dfrac{1}{2}\).
• A continuación usamos aquellas fracciones en las que la suma del numerador y denominador es 4. Entonces\(f(4) = \dfrac{1}{3}\),\(f(5) = \dfrac{3}{1}\). Nos saltamos\(\dfrac{2}{2}\) desde entonces\(\dfrac{2}{2} = \dfrac{1}{1}\). De esta manera, nos aseguraremos de que la función f sea una función uno a uno.

Ahora continuamos con diagonales sucesivas omitiendo fracciones que no están en términos más bajos. Este proceso garantiza que la función\(f\) será una inyección y una sobreyección. Por lo tanto,\(\mathbb{N} \thickapprox \mathbb{Q}^{+}\) y\(\text{card}(\mathbb{Q}^{+}) = \aleph_0\).

Nota: Para otra prueba del Teorema 9.14, véase el ejercicio (14) en la página 475.

Ya que\(\mathbb{Q}^{+}\) es contable, parece razonable esperar que eso\(Q\) sea contable. Pronto exploraremos esto. Por otra parte, en este punto, también puede parecer razonable preguntar,

“¿Hay conjuntos incontables?”

La respuesta a esta pregunta es sí, pero esperaremos hasta la siguiente sección para demostrar que ciertos conjuntos son incontables. Todavía tenemos algunos temas más que tratar en relación con los conjuntos contables.

Conjuntos infinitos contables

Teorema 9.15.

Si\(A\) es un conjunto infinitamente contable, entonces\(A \cup \{x\}\) es un conjunto infinitamente contable.

Prueba

\(A\)Sea un conjunto contablemente infinito. Entonces existe una biyección\(f: \mathbb{N} \to A\). Ya que\(x\) está en\(A\) o no en\(A\), podemos considerar dos casos.

Si\(x \in A\), entonces\(A \cup \{x\} = A\) y\(A \cup \{x\}\) es contablemente infinito.

Si\(x \notin A\), defina\(g: \mathbb{N} \to A \cup \{x\}\) por

\(g(n) = \begin{cases} x & \text{ if \(n = 1\)}\\ f (n - 1) &\ texto {si\(n > 1\).} \ end {casos}\)

La prueba de que la función\(g\) es una biyección es Ejercicio (4). Ya que\(g\) es una biyección, hemos demostrado que\(A \cup \{x\} \thickapprox \mathbb{N}\) y por lo tanto,\(A \cup \{x\}\) es un conjunto contablemente infinito.

Teorema 9.16.

Si\(A\) es un conjunto infinitamente contable y\(B\) es un conjunto finito, entonces\(A \cup B\) es un conjunto infinitamente contable.

Prueba

Ejercicio (5) en la página 474.

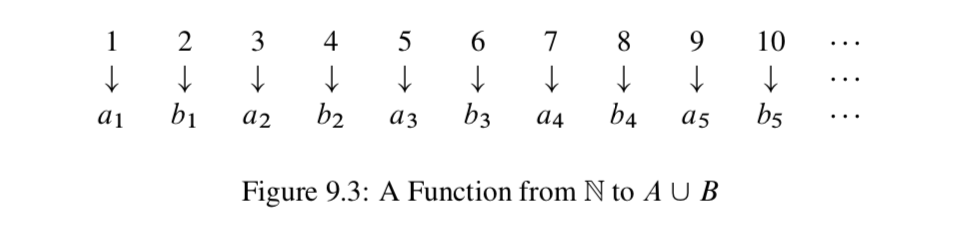
El teorema 9.16 dice que si agregamos un número finito de elementos a un conjunto contablemente infinito, el conjunto resultante sigue siendo contablemente infinito. Es decir, la cardinalidad del nuevo conjunto es la misma que la cardinalidad del conjunto original. Los conjuntos finitos se comportan de manera muy diferente en el sentido de que si agregamos elementos a un conjunto finito, cambiaremos la cardinalidad. Lo que incluso puede ser más sorprendente es el resultado en el Teorema 9.17 que afirma que la unión de dos conjuntos contablemente infinitos (disjuntos) es contablemente infinita. La prueba de este resultado es similar a la prueba de que los enteros son contablemente infinitos (Teorema 9.13). De hecho, si\(A = \{a_1, a_2, a_3, ...\}\) y\(B = \{b_1, b_2, b_3, ...\}\), entonces podemos usar el siguiente diagrama para ayudar a definir una biyección de\(\mathbb{N}\) a\(A \cup B\).

Teorema 9.17

Si\(A\) y\(B\) son conjuntos disjuntos contablemente infinitos, entonces\(A \cup B\) es un conjunto contablemente infinito.

Prueba

Dejar\(A\) y\(B\) ser conjuntos contablemente infinitos y dejar\(f: \mathbb{N} \to A\) y\(g: \mathbb{N} \to B\) ser bijecciones. Definir\(h: \mathbb{N} \to A \cup B\) por

\(h(n) = \begin{cases} f(\dfrac{n + 1}{2}) & \text{ if \(n\)es impar}\\ g (\ dfrac {n} {2}) &\ texto {si\(n\) es par.} \ end {casos}\)

Se deja como Ejercicio (6) en la página 474 para demostrar que la función\(h\) es una biyección.

Dado que podemos escribir el conjunto de números racionales Q como la unión del conjunto de números racionales no negativos y el conjunto de números racionales, podemos usar los resultados del Teorema 9.14, Teorema 9.15 y Teorema 9.17 para probar el siguiente teorema.

Teorema 9.18.

El conjunto\(\mathbb{Q}\) de todos los números racionales es contablemente infinito.

Prueba

Ejercicio (7) en la página 474.

En la Sección 9.1, probamos que cualquier subconjunto de un conjunto finito es finito (Teorema 9.6). Se debe esperar un resultado similar para los conjuntos contables. Primero probamos que cada subconjunto de\(\mathbb{N}\) es contable. Para un subconjunto infinito\(B\) de\(\mathbb{N}\), la idea de la prueba es definir una función\(g: \mathbb{N} \to B\) eliminando los elementos\(B\) desde el más pequeño hasta el siguiente más pequeño al siguiente más pequeño, y así sucesivamente. Hacemos esto definiendo la función\(g\) recursivamente de la siguiente manera:

• Dejar\(g(1)\) ser el número natural más pequeño en\(B\).
• Retirar\(g(1)\) de B y dejar que\(g(2)\) sea el número natural más pequeño en\(B - \{g(1)\}\).
• Retirar\(g(2)\) y dejar\(g(3)\) que sea el número natural más pequeño en\(B - \{g(1), g(2)\}\).
• Continuamos con este proceso. La definición formal recursiva de\(g: \mathbb{N} \to B\) se incluye en la prueba del Teorema 9.19.

Teorema 9.19.

Cada subconjunto de los números naturales es contable.

Prueba

Dejar\(B\) ser un subconjunto de\(\mathbb{N}\). Si\(B\) es finte, entonces\(B\) es contable. Entonces, a continuación asumimos que\(B\) es infinito. A continuación daremos una definición recursiva de una función\(g: \mathbb{N} \to B\) y luego probaremos que\(g\) es una biyección.

• Dejar\(g(1)\) ser el número natural más pequeño en\(B\).
• Para cada uno\(n \in \mathbb{N}\), el conjunto no\(B - \{g(1), g(2), ..., g(n)\}\) está vacío ya que\(B\) es infinte. Definir\(g(n + 1)\) para ser el número natural más pequeño en\(B - \{g(1), g(2), ..., g(n)\}\).

La prueba de que la función g es una bijección es Ejercicio (11) en la página 475.

Corolario 9.20.

Cada subconjunto de un conjunto contable es contable.

Prueba

Ejercicio (12) en la página 475.

Ejercicio 9.2

1. Declarar si cada uno de los siguientes es verdadero o falso.
   
   (a) Si un conjunto\(A\) es contablemente infinito, entonces\(A\) es infinito.
   (b) Si un conjunto\(A\) es contablemente infinito, entonces\(A\) es contable.
   (c) Si un conjunto\(A\) es incontable, entonces no\(A\) es contablemente infinito.
   (d) Si\(A \thickapprox \mathbb{N}_k\) para algunos\(k \in \mathbb{N}\), entonces no\(A\) es contable.
2. Demostrar que cada uno de los siguientes conjuntos es contablemente infinito.
   
   (a) El conjunto\(F^{+}\) de todos los números naturales que son múltiplos de 5
   (b) El conjunto\(F\) de todos los enteros que son múltiplos de 5
   \(\{\dfrac{1}{2^k}\ |\ k \in \mathbb{N}\}\)
   (c) (d)\ {n\ in\ mathbb {Z}\ |\ n\ ge -10\}\)
   (e) \(\mathbb{N} - \{4, 5, 6\}\)
   f)\(\{m \in \mathbb{Z}\ |\ m \equiv 2\text{ (mod 3)\}\)
3. Demostrar parte (2) del Teorema 9.10.
   Dejar\(A\) y\(B\) ser conjuntos. Si\(A\) es infinito y\(A \subseteq B\), entonces\(B\) es infinito.
4. Completar la prueba del Teorema 9.15 demostrando lo siguiente:
   Dejar\(A\) ser un conjunto contablemente infinito y\(x \notin A\). Si\(f: \mathbb{N} \to A\) es una biyección, entonces\(g\) es una biyección, donde\(g: \mathbb{N} \to A \cup \{x\}\) por
   \[g(n) = \begin{cases} x & \text{ if \(n = 1\)} \\ f(n - 1) & \text{ if \(n > 1\).} \end{cases}\]
5. Demostrar Teorema 9.16.
   Si\(A\) es un conjunto infinitamente contable y\(B\) es un conjunto finito, entonces\(A \cup B\) es un conjunto infinitamente contable.

   Sugerencia: Deje la tarjeta (\(B\))\(= n\) y use una prueba por inducción en\(n\). El teorema 9.15 es el paso base.

6. Completar la prueba del Teorema 9.17 demostrando lo siguiente:
   Dejar\(A\) y\(B\) ser disjuntos contablemente infinitos conjuntos y dejar\(f: \mathbb{N} \to A\) y\(g: \mathbb{N} \to B\) ser bijecciones. Definir\(h: \mathbb{N} \to A \cup B\) por
   \[h(n) = \begin{cases} f(\dfrac{n + 1}{2} & \text{ if \(n\) is odd} \\ g(\dfrac{n}{2}) & \text{ if \(n\) is even.} \end{cases}\]
   Entonces la función\(h\) es una biyección.
7. Demostrar Teorema 9.18.
   El conjunto\(\mathbb{Q}\) de todos los números racionales es contable.
   Pista: Utilice el Teorema 9.15 y el Teorema 9.17.
8. Demostrar que si\(A\) es contablemente infinito y\(B\) es finito, entonces\(A - B\) es contablemente infinito.
9. Definir de la\(f: \mathbb{N} \times \mathbb{N} \to \mathbb{N}\) siguiente manera: Para cada uno\((m, n) \in \mathbb{N} \times \mathbb{N}\),
   \[f(m, n) = 2^{m-1}(2n - 1).\]
   
   (a) Demostrar que\(f\) es una inyección. Sugerencia: Si\(f(m, n) = f(s, t)\), hay tres casos a considerar:\(m > s\),\(m < s\), y\(m = s\). Utilizar leyes de exponentes para demostrar que los dos primeros casos conducen a una contradicción.
   b) Demostrar que\(f\) es una sobrejección. Sugerencia: Puede usar el hecho de que si\(y \in \mathbb{N}\), entonces\(y = 2^{k}x\), donde\(x\) es un número natural impar y\(k\) es un entero no negativo. Esto es en realidad una consecuencia del Teorema Fundamental de la Aritmética, Teorema 8.15. [Ver Ejercicio (13) en la Sección 8.2.]
   c) Demostrar eso\(\mathbb{N} \times \mathbb{N}\thickapprox \mathbb{N}\) y de ahí esa tarjeta\((\mathbb{N} \times \mathbb{N}) = \aleph_{0}\).
10. Usa Ejercicio (9) para probar que si\(A\) y\(B\) son conjuntos infinitos contables, entonces\(A \times B\) es un conjunto infinitamente contable.
11. Completar la prueba del Teorema 9.19 demostrando que la función\(g\) definida en la prueba es una biyección de\(\mathbb{N}\) a\(B\).

    Pista: Para probar que\(g\) es una inyección, podría ser más fácil probarlo para todos\(r, s \in \mathbb{N}\), si\(r \ne s\), entonces\(g(r) \ne g(s)\). Para ello, podemos suponer que\(r < s\) ya que uno de los dos números debe ser menor que el otro. Entonces fíjese en eso\(g(r) \in \{g(1), g(2), ..., g(s - 1)\}\).

    Para probar que\(g\) es una surjección, dejemos\(b \in B\) y notemos que para algunos\(k \in \mathbb{N}\), habrá números\(k\) naturales en\(B\) que son menores que\(b\).

12. Probar Corolario 9.20, que establece que cada subconjunto de un conjunto contable es contable.

    Pista: Vamos\(S\) a ser un conjunto contable y asumir que\(A \subseteq S\). Hay dos casos:\(A\) es finito o\(A\) es infinito. Si\(A\) es infinito, deja\(f: S \to \mathbb{N}\) ser una bijección y definirlo\(g: A \to f(A)\) por\(g(x) = f(x)\), para cada uno\(x \in A\).

13. Usa Corolario 9.20 para probar que el conjunto de todos los números racionales entre 0 y 1 es contablemente infinito.
    
    Exploraciones y actividades
14. Otra Prueba que\(\mathbb{Q}^{+}\) Es Contable. Para esta actividad, puede ser útil utilizar el Teorema Fundamental de la Aritmética (ver Teorema 8.15 en la página 432). \(\mathbb{Q}^{+}\)Sea el conjunto de números racionales positivos. Cada número racional positivo tiene una representación única como fracción\(\dfrac{m}{n}\), donde\(m\) y\(n\) son números naturales relativamente primos. Ahora vamos a definir una función de la\(f: \mathbb{Q}^{+} \to \mathbb{N}\) siguiente manera:
    
    Si\(x \in \mathbb{Q}^{+}\) y\(x = \dfrac{m}{n}\), donde\(m, n \in \mathbb{N}\),\(n \ne 1\) y gcd\((m, n) = 1\), escribimos
    \[\begin{array} {rcl} {m} &= & {p_{1}^{\alpha_1} p_{2}^{\alpha_2} \cdot\cdot\cdot p_{r}^{\alpha_r},\text{ and}} \\ {n} &= & {q_{1}^{\beta_1} q_{2}^{\beta_2} \cdot\cdot\cdot q_{s}^{\beta_s},} \end{array}\]
    donde\(p_{1}, p_{2}, ..., p_{r}\) son distintos números primos,\(q_{1}, q_{2}, ..., q_{s}\) son números primos distintos, y\(\alpha_{1}, \alpha_{2}, ..., \alpha_{r}\) y\(\beta_{1}, \beta_{2}, ..., \beta_{s}\) son números naturales.
    También escribimos\(1 = 2^{0}\) cuándo\(m = 1\). Entonces definimos
    \[f(x) = p_{1}^{2\alpha_1} p_{2}^{2\alpha_2} \cdot\cdot\cdot p_{r}^{2\alpha_r} q_{1}^{2\beta_1 - 1} q_{2}^{2\beta_2 - 1} \cdot\cdot\cdot q_{s}^{2\beta_s - 1}.\]
    Si\(x = \dfrac{m}{1}\), entonces definimos\(f(x) = p_{1}^{2\alpha_1} p_{2}^{2\alpha_2} \cdot\cdot\cdot p_{r}^{2\alpha_r} = m^2\).
    
    (a) Determinar\(f(\dfrac{2}{3})\)\(f(\dfrac{5}{6})\),\(f(6)\),\(f(\dfrac{12}{25})\),\(f(\dfrac{375}{392})\), y\(f(\dfrac{2^3 \cdot 11^3}{3 \cdot 5^4})\).
    b) Si es posible, encontrar\(x \in \mathbb{Q}^{+}\) tal que\(f(x) = 100\).
    c) De ser posible, encontrar\(x \in \mathbb{Q}^{+}\) tal que\(f(x) = 12\).
    d) De ser posible, encontrar\(x \in \mathbb{Q}^{+}\) tal que\(f(x) = 2^8 \cdot 3^5 \cdot 13 \cdot 17^2\).
    e) Demostrar que la función\(f\) es una inyección.
    f) Demostrar que la función\(f\) es una sobrejección.
    g) ¿Qué se ha demostrado?

Responder

Agrega textos aquí. No elimine primero este texto.