9.3: Conjuntos incontables

Vista previa de la actividad\(\PageIndex{1}\): The Game of Dodge Ball

(Desde el corazón de las matemáticas: una invitación al pensamiento efectivo por Edward B. Burger y Michael Starbird, Key Publishing Company, 2000 por Edward B. Burger y Michael Starbird.)

Dodge Ball es un juego para dos jugadores. Se juega en un tablero de juego como el que se muestra en la Figura 9.4. El Jugador Uno tiene una matriz de 6 por 6 para completar y el Jugador Dos tiene una fila de 1 por 6 para completar. Cada jugador tiene seis turnos como se describe a continuación.

• El Jugador Uno comienza rellenando la primera fila horizontal de su tabla con una secuencia de seis X's y O's, una en cada cuadrado de la primera fila.
• Entonces el Jugador Dos coloca ya sea una X o una O en la primera caja de su fila. En este punto, el Jugador Uno ha completado la primera fila y el Jugador Dos ha llenado la primera casilla de su fila con una letra.
  
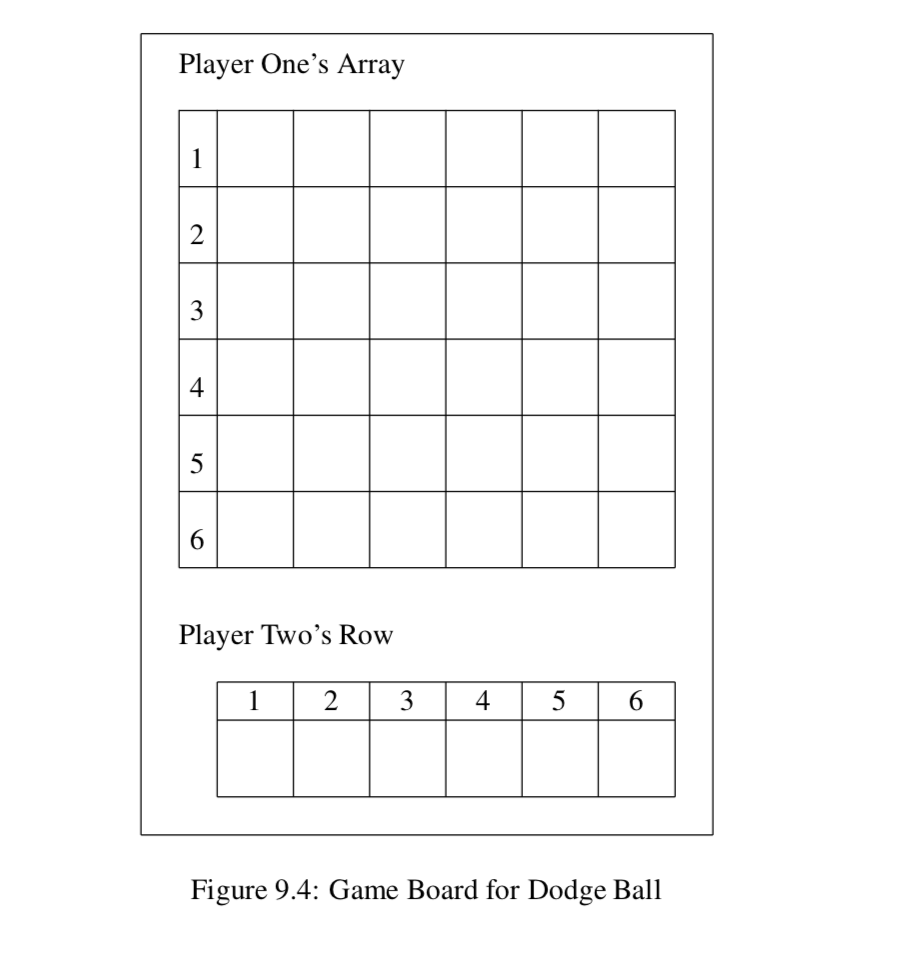
• El juego continúa con el Jugador Uno completando una fila con seis letras (X's y O's), una en cada casilla de la siguiente fila seguida por el Jugador Dos escribiendo una letra (una X o una O) en la siguiente casilla de su fila. El juego se completa cuando el Jugador Uno haya completado las seis filas y el Jugador Dos haya completado las seis casillas de su fila.

Ganar el juego

• El Jugador Uno gana si alguna fila horizontal en la matriz 6 por 6 es idéntica a la fila que el Jugador Dos creó. (El Jugador Uno coincide con el Jugador Dos.)
• El Jugador Dos gana si la fila de seis letras del Jugador Dos es diferente a cada una de las seis filas producidas por el Jugador Uno. (El Jugador Dos “esquiva” al Jugador Uno.)

Hay una estrategia ganadora para uno de los dos jugadores. Esto quiere decir que hay un plan por el cual uno de los dos jugadores siempre ganará. ¿Qué jugador tiene una estrategia ganadora? Describa cuidadosamente esta estrategia ganadora.

Aplicación de la estrategia ganadora a listas de números reales

A continuación se presenta una lista de números reales entre 0 y 1. Cada número real se escribe como un número decimal.

\(a_1 = 0.1234567890\)\(a_6 = 0.0103492222\)
\(a_2 = 0.3216400000\)\(a_7 = 0.0011223344\)
\(a_3 = 0.4321593333\)\(a_8 = 0.7077700022\)
\(a_4 = 0.9120930092\)\(a_9 = 0.2100000000\)
\(a_5 = 0.0000234102\)\(a_{10} = 0.9870008943\)

Usa un método similar a la estrategia ganadora en el dodge ball de Cantor para escribir un número real (en forma decimal) entre 0 y 1 que no esté en esta lista de 10 números.

1. ¿Crees que tu método podría ser usado para cualquier lista de 10 números reales entre 0 y 1 si el objetivo es escribir un número real entre 0 y 1 que no esté en la lista?
2. ¿Crees que este método podría extenderse a una lista de 20 números reales diferentes? ¿A una lista de 50 números reales diferentes?
3. ¿Crees que este método podría extenderse a una lista que consiste en una lista contablemente infinita de números reales?

Vista previa de la actividad\(\PageIndex{2}\): Functions from a Set to Its Power Set

\(A\)Déjese ser un conjunto. En la Sección 5.1, definimos el conjunto\(\mathcal{P}(A)\) de potencias\(A\) de como el conjunto de todos los subconjuntos de\(A\). Esto significa que

\(X \in \mathcal{P}(A)\)si y sólo si\(X \subseteq A\).

El Teorema 5.5 en la Sección 5.1 establece que si un conjunto\(A\) tiene n elementos, entonces\(A\) tiene\(2^{n}\) subconjuntos o que\(\mathcal{P}(A)\) tiene\(2^{n}\) elementos. Usando nuestra notación actual para cardinalidad, esto significa que

si tarjeta\((A) = n\), luego tarjeta\((\mathcal{P}(A) = 2^{n}\).

(La prueba de este teorema fue Ejercicio (17) en la página 229.)

Ahora vamos a definir y explorar algunas funciones desde un conjunto\(A\) hasta su conjunto de potencia\(\mathcal{P}(A)\). Esto significa que la entrada de la función será un elemento de\(A\) y la salida de la función será un subconjunto de\(A\).

1. Vamos\(A = \{1, 2, 3, 4\}\). Definir\(f: A \to \mathcal{P}(A)\) por
   \(f(1) = \{1, 2, 3\}\)\(f(3) = \{1, 4\}\)
   \(f(2) = \{1, 3, 4\}\)\(f(4) = \{2, 4\}\).
   
   (a) ¿Es\(1 \in f(1)\)? ¿Es\(2 \in f(2)\)? ¿Es\(3 \in f(3)\)? ¿Es\(4 \in f(4)\)?
   b) Determinar\(S = \{x \in A\ |\ x \notin f(x)\}\).
   (c) Obsérvese que\(S \in \mathcal{P}(A)\). ¿Existe un elemento\(t\) en\(A\) tal que\(f(t) = S\)? Es decir, ¿es\(S \in \text{range}(f)\)?
2. Vamos\(A = \{1, 2, 3, 4\}\). Definir\(f: A \to \mathcal{P}(A)\) por\[f(x) = A - \{x\} \text{ for each } x \in A.\]
   (a) Determinar\(f(1)\). ¿Es\(1 \in f(1)\)?
   b) Determinar\(f(2)\). ¿Es\(2 \in f(2)\)?
   (c) Determinar\(f(3)\). ¿Es\(3 \in f(3)\)?
   d) Determinar\(f(4)\). ¿Es\(4 \in f(4)\)?
   e) Determinar\(S = \{x \in A\ |\ x \notin f(x)\}\).
   f) Obsérvese que\(S \in \mathcal{P}(A)\). ¿Existe un elemento\(t\) en\(A\) tal que\(f(t) = S\)? Es decir, ¿es\(S \in \text{range}(f)\)?
3. Definir\(f: \mathbb{N} \to \mathcal{P}(\mathbb{N})\) por
   \[f(n) - \mathbb{N} - \{n^2, n^2 - 2n\} \text{, for each} n \in \mathbb{N}.\]
   (a) Determinar\(f(1)\)\(f(2)\),,\(f(3)\), y\(f(4)\). En cada uno de estos casos, determinar si\(k \in f(k)\).
   b) Demostrar que si\(n > 3\), entonces\(n \in f(n)\). Pista: Demostrar que si\(n > 3\), entonces\(n^2 > n\) y\(n^2 - 2n > n\).
   (c) Determinar\(S = \{x \in \mathbb{N}\ |\ x \notin f(x)\}\).
   d) Obsérvese que\(S \in \mathcal{P}(\mathbb{N})\). ¿Existe un elemento\(t\) en\(\mathbb{N}\) tal que\(f(t) = S\)? Es decir, ¿es\(S \in \text{range}(f)\)?

Hemos visto ejemplos de conjuntos que son contablemente infinitos, pero aún no hemos visto un ejemplo de un conjunto infinito que sea incontable. Lo haremos en esta sección. El primer ejemplo de un conjunto incontable será el intervalo abierto de números reales (0, 1). La prueba de que este intervalo es incontable utiliza un método similar a la estrategia ganadora para el Jugador Dos en el juego de Dodge Ball de la Actividad Previa 1. Antes de considerar la prueba, necesitamos exponer un resultado importante sobre las expresiones decimales para números reales.

Expresiones decimales para números reales

En su forma decimal, cualquier número real a en el intervalo (0, 1) puede escribirse como\(a = 0.a_{1}a_{2}a_{3}a_{4} ...\), donde cada uno\(a_i\) es un número entero con\(0 \le a_i \le 9\). Por ejemplo,

\(\dfrac{5}{12} = 0.416666...\)

A menudo abreviamos esto como\(\dfrac{5}{12} = 0.41\bar{6}\) para indicar que el 6 se repite. También podemos repetir un bloque de dígitos. Por ejemplo,\(\dfrac{5}{26} = 0.19\overline{230769}\) para indicar que el bloque 230769 se repite. Eso es

\(\dfrac{5}{26} = 0.19230769230769230769...\)

Sólo hay una situación en la que un número real se puede representar como decimal en más de una forma. Un decimal que termina con una cadena infinita de 9's es igual a uno que termina con una cadena infinita de 0's. Por ejemplo, 0.3199999.... representa el mismo número real que 0.3200000.... Las series geométricas se pueden utilizar para demostrar que un decimal que termina con una cadena infinita de 9's es igual a uno que termina con una cadena infinita de 0's, pero no lo haremos aquí.

Definición

Una representación decimal de un número real\(a\) está en forma normalizada siempre que no exista un número natural\(k\) tal que para todos los números naturales\(n\) con\(n > k\),\(a_n = 9\). Es decir, la representación decimal de\(a\) está en forma normalizada si y sólo si no termina con una cadena infinita de 9's.

Una razón por la que la forma normalizada es importante es el siguiente teorema (que no se probará aquí).

Teorema 9.21

Dos números decimales en forma normalizada son iguales si y solo si tienen dígitos idénticos en cada posición decimal.

Incontables subconjuntos de\(\mathbb{R}\)

En la prueba que sigue, utilizaremos únicamente la forma normalizada para la representación decimal de un número real en el intervalo (0, 1).

Teorema 9.22.

El intervalo abierto (0, 1) es un conjunto incontable.

Prueba

Dado que el intervalo (0, 1) contiene el subconjunto infinito�≡\(\{\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, ...\}\), podemos usar el Teorema 9.10, para concluir que (0, 1) es un conjunto infinito. Entonces (0, 1) es o bien contablemente infinito o incontable. Demostraremos que (0, 1) es incontable al probar que cualquier inyección de (0, 1) a\(\mathbb{N}\) no puede ser una sobreyección, y por lo tanto, no hay bijección entre (0, 1) y\(\mathbb{N}\).

Entonces supongamos que la función\(f: \mathbb{N} \to (0, 1)\) es una inyección. Mostraremos que\(f\) no puede ser una surjección al mostrar que existe un elemento en (0, 1) que no puede estar en el rango de\(f\). Escribiendo las imágenes de los elementos de\(\mathbb{N}\) en forma normalizada, podemos escribir

\(f(1) = 0.a_{11} a_{12} a_{13} a_{14} a_{15} ...\)
\(f(2) = 0.a_{21} a_{22} a_{23} a_{24} a_{25} ...\)
\(f(3) = 0.a_{31} a_{32} a_{33} a_{34} a_{35} ...\)
\(f(4) = 0.a_{41} a_{42} a_{43} a_{44} a_{45} ...\)
\(f(5) = 0.a_{51} a_{52} a_{53} a_{54} a_{55} ...\)
...
\(f(n) = 0.a_{n1} a_{n2} a_{n3} a_{n4} a_{n5} ...\)
...

Observe el uso de los subíndices dobles. El número\(a_{ij}\) es el dígito\(j\) th a la derecha del punto decimal en la representación decimal normalizada de\(f(i)\).

Ahora construiremos un número real\(b = 0.b_{1} b_{2} b_{3} b_{4} b_{5} ...\) en (0, 1) y en forma normalizada que no esté en esta lista.

Nota: La idea es comenzar en la esquina superior izquierda y bajar la diagonal de una manera similar a la estrategia ganadora para el Jugador Dos en el juego en la Actividad Previa 1. En cada paso, elegimos un dígito que no es igual al dígito diagonal.

Empezar con\(a_{11}\) en\(f(1)\). Queremos elegir para\(b_1\) que\(b_1 \ne 0\),\(b_1 \ne a_{11}\), y\(b_1 \ne 9\). (Para asegurarnos de que terminemos con un decimal que esté en forma normalizada, nos aseguramos de que cada dígito no sea igual a 9.) Luego repetimos este proceso con\(a_{22}\),\(a_{33}\),\(a_{44}\),\(a_{55}\), y así sucesivamente. Entonces dejamos\(b\) ser el número real\(b = 0.b_{1} b_{2} b_{3} b_{4} b_{5} ...\), donde para cada\(k \in \mathbb{N}\)

\(b_k = \begin{cases} 3 & \text{ if \(a_{kk} \ne 3\)}\\ 5 &\ texto {si\(a_{kk} = 3\).} \ end {casos}\)

(La elección de 3 y 5 es arbitraria. Otras opciones de dígitos distintos también funcionarán.)

Ahora para cada uno\(n \in \mathbb{N}\),\(b \ne f(n)\) ya que\(b\) y\(f(n)\) están en forma normalizada\(b\) y y\(f(n)\) difieren en el lugar decimal\(n\) th. Esto demuestra que cualquier función de\(\mathbb{N}\) a (0, 1) no puede ser sobreyección y por lo tanto, no hay bijección de\(\mathbb{N}\) a (0, 1). Por lo tanto, (0, 1) no es contablemente infinito y por lo tanto debe ser un conjunto incontable.

Comprobación de Progreso 9.23 (Dodge Ball y Argumento Diagonal de Cantor)

La prueba del Teorema 9.22 suele ser referida como argumento diagonal de Cantor. Lleva el nombre del matemático Georg Cantor, quien publicó por primera vez la prueba en 1874. Explica la conexión entre la estrategia ganadora para el Jugador Dos en Dodge Ball (ver Actividad Previa 1) y la prueba del Teorema 9.22 usando el argumento diagonal de Cantor.

Contestar

Agrega textos aquí. No elimine primero este texto.

El intervalo abierto (0, 1) es nuestro primer ejemplo de un conjunto incontable. El número cardinal de (0, 1) se define como\(c\), que significa el número cardinal del continuum. Entonces los dos números cardinales infinitos que hemos visto son\(\aleph_0\) para conjuntos contablemente infinitos y\(c\).

Definición

\(A\)Se dice que un conjunto tiene cardinalidad\(c\) siempre que\(A\) sea equivalente a (0, 1). En este caso, escribimos tarjeta\((A) = c\) y decimos que el número cardinal de\(A\) es\(c\).

El comprobante del Teorema 9.24 se incluye en la Comprobación de Progreso 9.25.

Teorema 9.24.

Dejar\(a\) y\(b\) ser números reales con\(a < b\). El intervalo abierto\((a, b)\) es incontable y tiene cardinalidad\(c\).

Prueba

Agrega prueba aquí y automáticamente se ocultará

Comprobación de Progreso 9.25 (Prueba de Teorema 9.24)

1. En la Parte (3) de la Comprobación de Progreso 9.2, probamos que si\(b \in \mathbb{R}\) y\(b > 0\), entonces el intervalo abierto (0, 1) es equivalente al intervalo abierto (0,\(b\)). Ahora vamos\(a\) y\(b\) sean números reales con\(a < b\). Encuentra una función
   \[f: (0, 1) \to (a, b)\]
   que sea una biyección y concluya que\((0, 1) \thickapprox (a, b)\).
   Sugerencia: Encuentra una función lineal que pase por los puntos (0,\(a\)) y (1,\(b\)). Usa esto para definir la función\(f\). Asegúrate de demostrar que esta función\(f\) es una biyección.
2. \(a, b, c, d\)Dejen ser números reales con\(a < b\) y\(c < d\). \((a, b) \thickapprox (c, d)\)Demuéstralo.

Contestar

Agrega textos aquí. No elimine primero este texto.

---

Teorema 9.26.

El conjunto de números reales\(\mathbb{R}\) es incontable y tiene cardinalidad\(c\).

Prueba

Dejar\(f: (-\dfrac{\pi}{2}, \dfrac{\pi}{2}) \to \mathbb{R}\) ser definido por\(f(x) = tan x\), para cada uno\(x \in \mathbb{R}\). La función\(f\) es como biyección y, por lo tanto,\((-\dfrac{\pi}{2}, \dfrac{\pi}{2}) \thickapprox \mathbb{R}\). Entonces por el Teorema 9.24,\(\mathbb{R}\) es incontable y tiene cardinalidad\(c\).

Teorema de Cantor

Ahora hemos visto dos números cardinales infinitos diferentes,\(\aleph_0\) y\(c\). Puede parecer sorprendente que haya más de un número cardinal infinito. Una pregunta razonable en este punto es: “¿Hay otros números cardinales infinitos?” La respuesta asombrosa es que hay, y de hecho, hay infinitamente muchos números cardinales infinitos diferentes. La base de este hecho es el siguiente teorema, que establece que un conjunto no es equivalente a su conjunto de potencia. La prueba se debe a Georg Cantor (1845—1918), y la idea de esta prueba se exploró en la Actividad 2 de Vista Previa. La idea básica de la prueba es probar que cualquier función de un conjunto\(A\) a su conjunto de potencia no puede ser una sobreyección.

Teorema 9.27 (Teorema de Cantor).

Por cada conjunto\(A\),\(A\) y\(\mathcal{P}(A)\) no tienen la misma cardinalidad.

Prueba

\(A\)Déjese ser un conjunto. Si\(A = \emptyset\), entonces\(\mathcal{P}(A) = \{\emptyset\}\), que tiene cardinalidad 1. Por lo tanto,\(\emptyset\) y\(\mathcal{P}(\emptyset)\) no tienen la misma cardinalidad.

Ahora supongamos eso\(A \ne \emptyset\), y vamos\(f: A \to \mathcal{P}(A)\). Demostraremos que\(f\) no puede ser una sobrejección, y por lo tanto no hay bijección de\(A\) a\(\mathcal{P}(A)\). Esto demostrará que no\(A\) es equivalente a\(\mathcal{P}(A)\). Definir

\(S = \{x \in A\ |\ x \notin f(x)\}\).

Supongamos que existe un\(t\) en\(A\) tal que\(f(t) = S\). Ahora bien, ya sea\(f \in S\) a\(t \notin S\).

• Si\(t \in S\), entonces\(t \in \{x \in A\ |\ x \notin f(x)\}\). Por la definición de\(S\), esto significa que\(t \notin f(t)\). Sin embargo,\(f(t) = S\) y así concluimos eso\(t \notin S\). Pero ahora tenemos\(t \in S\) y\(t \notin S\). Esto es una contradicción.
• Si\(t \notin S\), entonces\(t \notin \{x \in A\ |\ x \notin f(x)\}\). Por la definición de\(S\), esto significa que\(t \in f(t)\). Sin embargo,\(f(t) = S\) y así concluimos eso\(t \in S\). Pero ahora tenemos\(t \notin S\) y\(t \in S\). Esto es una contradicción.

Entonces en ambos casos hemos llegado a una contradicción. Esto quiere decir que no existe una\(t\) en\(A\) tal que\(f(t) = S\). Por lo tanto, cualquier función de\(A\) a no\(\mathcal{P}(A)\) es una sobreyección y por lo tanto no una biyección. De ahí,\(A\) y\(\mathcal{P}(A)\) no tienen la misma cardinalidad.

corolario 9.28.

\(\mathcal{P}(\mathbb{N})\)es un conjunto infinito que no es contablemente infinito.

Prueba

Ya que\(\mathcal{P}(\mathbb{N})\) contiene el subconjunto infinito\(\{\{1\}, \{2\}, \{3\} ...\}\), podemos utilizar el Teorema 9.10, para concluir que\(\mathcal{P}(\mathbb{N})\) es un conjunto infinito. Por el Teorema de Cantor (Teorema 9.27),\(\mathbb{N}\) y\(\mathcal{P}(\mathbb{N})\) no tienen la misma cardinalidad. Por lo tanto, P.N/ no es contable y por lo tanto es un conjunto incontable.

Algunos comentarios finales sobre Uncountable Sets

1. Ahora hemos visto que cualquier intervalo abierto de números reales es incontable y tiene cardinalidad c. Además, R es incontable y tiene cardinalidad c. Ahora, el Corolario 9.28 nos dice que P.N/ es incontable. Una pregunta que se puede hacer es,
   \[\text{“Does \(\mathcal{P}(\mathbb{N})\) have the same cardinality as \(\mathbb{R}\)?”}\]
   La respuesta es sí, aunque todavía no estamos en condiciones de demostrarlo. Una prueba de este hecho utiliza el siguiente teorema, que se conoce como el Teorema de Cantor-Schr\(\ddot{o}\) Der-Bernstein.

   Teorema 9.29. Cantor-Schr\(\ddot{o}\)der-Bernstein

   Dejar\(A\) y\(B\) ser conjuntos. Si existen inyecciones\(f: A \to B\) y\(g: B \to A\), entonces\(A \thickapprox B\)

   En el enunciado de este teorema, observe que no se requiere que la función\(g\) sea la inversa de la función\(f\). No vamos a probar aquí el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein. Los siguientes ítems mostrarán algunos usos de este importante teorema.
2. El Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein también se puede utilizar para demostrar que el intervalo cerrado [0, 1] es equivalente al intervalo abierto (0, 1). Consulte Ejercicio (6) en la página 486.
3. Otra cuestión que se planteó anteriormente es,
   \[\text{“Are there other infinite cardinal numbers other than \(\aleph_0\) and \(c\)?”}\]

   Nuevamente, la respuesta es sí, y la base para ello es el Teorema de Cantor (Teorema 9.27). Podemos comenzar con tarjeta\((\mathbb{N}) = \aleph_0\). Luego definimos los siguientes números cardinales infinitos: El teorema de
   \[\begin{array} {lll} {\text{card}(\mathcal{P}(\mathbb{N})) = \alpha_1.} & & {\text{card}(\mathcal{P}(\mathcal(\mathcal(\mathbb{N})))) = \alpha_1.} \\ {\text{card}(\mathcal{P}(\mathcal(\mathbb{N}))) = \alpha_1.} & & {...} \end{array}\]
   Cantor nos dice que todos estos son números cardinales diferentes, por lo que solo estamos usando la letra griega minúscula\(\alpha\) (alfa) para ayudar a dar nombres a estos números cardinales. De hecho, aunque no lo vamos a definir aquí, hay una manera de “ordenar” estos números cardinales de tal manera que
   \[\aleph_0 < \alpha_1 < \alpha_2 < \alpha_3 < \cdot\cdot\cdot.\]
   tenga en cuenta, sin embargo, que aunque estos sean números cardinales diferentes, el Teorema de Cantor no nos dice que estos son los únicos cardenales números.

4. En Comentario (1), lo indicamos\(\mathcal{P}(\mathbb{N})\) y\(\mathbb{R}\) tenemos la misma cardinalidad. Combinando esto con la notación en Comentario (3), esto significa que

   \[\alpha_1 = c.\]

   Sin embargo, esto no significa necesariamente que\(c\) sea el “siguiente mayor” número cardinal después\(\aleph_0\). Una pregunta razonable es: “¿Hay un conjunto infinito con cardinalidad entre\(\aleph_0\) y\(c\)?” Reformulando esto en términos de la recta numérica real, la pregunta es: “En la recta numérica real, ¿hay un conjunto infinito de puntos que no es equivalente a toda la línea y tampoco equivalente al conjunto de números naturales?” Esta pregunta la hizo Cantor, pero no pudo encontrar ningún conjunto de ese tipo. Conjeturó que no existe tal conjunto. Es decir, conjeturó que ese\(c\) es realmente el siguiente número cardinal después\(\aleph_0\). Esta conjetura ha llegado a conocerse como la Hipótesis del Continuum. Declarada algo más formalmente, la Hipótesis del Continuum es

   \[\text{There is no set \(X\) such that \(\aleph_0 < \text{card}(X) < c\).}\]
   La cuestión de si la Hipótesis del Continuum es verdadera o falsa es uno de los problemas más famosos de las matemáticas modernas.

   A través del trabajo combinado de Kurt G\(\ddot{o}\) del en la década de 1930 y Paul Cohen en 1963, se ha demostrado que la Hipótesis del Continuum no puede ser probada o desmentida a partir de los axiomas estándar de la teoría de conjuntos. Esto significa que la Hipótesis del Continuum o su negación se pueden agregar a los axiomas estándar de la teoría de conjuntos sin crear una contradicción.

---

Ejercicio 9.3

1. Utilizar una biyección apropiada para demostrar que cada uno de los siguientes conjuntos tiene cardinalidad\(c\).
   
   (a) (0,\(\infty\))
   (b) (\(a\),\(\infty\)), para cualquier\(a \in \mathbb{R}\)
   (c)\(\mathbb{R} - \{0\}\)
   (d)\(\mathbb{R} - \{a\}\), para cualquier\(a \in \mathbb{R}\)
2. ¿El conjunto de números irracionales es contable o incontable? Demuestra que tu respuesta es correcta.
3. Demostrar que si\(A\) es incontable y\(A \subseteq B\), entonces\(B\) es incontable.
4. ¿Dos conjuntos incontables tienen siempre la misma cardinalidad? Justifica tu conclusión.
5. Dejar\(C\) ser el conjunto de todas las secuencias infinitas, cada una de cuyas entradas es el dígito 0 o el dígito 1. Por ejemplo,
   \[\begin{array} {rcl} {(1, 0, 1, 0, 1, 0, 1, 0, ...)} &\in & {C;} \\ {(0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, ...)} &\in & {C;} \\ {(2, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, ...)} &\notin & {C.} \end{array}\]
   ¿el conjunto es\(C\) un conjunto contable o un conjunto incontable? Justifica tu conclusión.
6. El objetivo de este ejercicio es utilizar el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein para demostrar que la cardinalidad del intervalo cerrado [0, 1] ≡ ╳ es\(c\).
   
   (a) Encontrar una inyección\(f:(0, 1) \to [0, 1]\).
   (b) Encontrar una inyección\(h:[0, 1] \to (-1, 2)\).
   c) Utilizar el hecho de que\((-1, 2) \thickapprox (0, 1)\) para probar que existe una inyección\(g: [0, 1] \to (0, 1)\). (Sólo es necesario probar que la inyección\(g\) existe. No es necesario determinar una fórmula específica para\(g(x)\).)
   Nota: En lugar de hacer la Parte (b) como se indica, otro enfoque es encontrar una inyección\(k: [0, 1] \to (0, 1)\). Entonces, es posible omitir la Parte (c) e ir directamente a la Parte (d).
   d) Utilizar el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein para concluir que\([0, 1] \thickapprox (0, 1)\) y de ahí que la cardinalidad de [0, 1] es\(c\).
7. En el Ejercicio (6), probamos que el intervalo cerrado [0, 1] es incontable y tiene cardinalidad\(c\). Ahora vamos\(a, b \in \mathbb{R}\) con\(a < b\). Demostrar eso\([a, b] \thickapprox [0, 1]\) y de ahí que\([a, b]\) sea contabilizable y tenga cardinalidad\(c\).
8. ¿Es el conjunto de todos los subconjuntos finitos de\(\mathbb{N}\) contables o incontables? Dejar\(F\) ser el conjunto de todos los subconjuntos finitos de\(\mathbb{N}\). Determinar la cardinalidad del conjunto\(F\).
   
   Considera definir una función\(f: F \to \mathbb{N}\) que produzca lo siguiente.
   \(\bullet\)Si\(A = \{1, 2, 6\}\), entonces\(f(A) = 2^{1}3^{2}5^{6}\).
   \(\bullet\)Si\(B = \{3, 6\}\), entonces\(f(B) = 2^{3}3^{6}\).
   \(\bullet\)Si\(C = \{m_{1}, m_{2}, m_{3}, m_{4}\}\) con\(m_{1} < m_{2} < m_{3} < m_{4}\), entonces\(f(C) = 2^{m_1} 3^{m_2} 5^{m_3} 7^{m_4}\).
   Podría ser útil usar el Teorema Fundamental de la Aritmética en la página 432 y para denotar el conjunto de todos los primos como\(P = \{p_1, p_2, p_3, p_4, ...\}\) con\(p_1 > p_2 < p_3 < p_4 \cdot\cdot\cdot\). Usando los conjuntos\(A\),\(B\), y\(C\) definir arriba, podríamos entonces escribir
   \(f(A) = p_{1}^{1}p_{2}^{2}p_{3}^{6}\),\(f(B) = p_{1}^{3}p_{2}^{6}\), y\(f(C) = p_{1}^{m_1} p_{2}^{m_2} p_{3}^{m_3} p_{4}^{m_4}\).
9. En el Ejercicio (2), demostramos que el conjunto de números irracionales es incontable. No obstante, todavía no conocemos la cardinalidad del conjunto de números irracionales. Observe que podemos usar\(\mathbb{Q}^c\) para representar el conjunto de números irracionales.
   
   (a) Construir una función\(f: \mathbb{Q}^c \to \mathbb{R}\) que sea una inyección.
   
   Sabemos que cualquier número real a se puede representar en forma decimal de la siguiente manera:
   \[a = A.a_{1}a_{2}a_{3}a_{4} \cdot\cdot\cdot a_{n} \cdot\cdot\cdot,\]
   donde\(A\) es un entero y la parte decimal (\(0.a_{1}a_{2}a_{3}a_{4} \cdot\cdot\cdot\)) está en forma normalizada. (Ver página 480.) También sabemos que el número real\(a\) es un número irracional si y sólo\(a\) tiene una expansión decimal infinita no repetitiva. Ahora nos asociamos con\(a\) el número real
   \[A.a_{1}0a_{2}11a_{3}000a_{4}1111a_{5}00000a_{6}111111 \cdot\cdot\cdot .\]
   Observe que para construir el número real en (9.3.12), comenzamos con la expansión decimal de a, insertamos un 0 a la derecha del primer dígito después del punto decimal, insertamos dos 1's a la derecha de la segundo dígito a la derecha del punto decimal, insertó tres 0's a la derecha del tercer dígito a la derecha del punto decimal, y así sucesivamente.
   
   b) Explicar por qué el número real en (9.3.12) es un número irracional.
   (c) Utilizar estas ideas para construir una función\(g: \mathbb{R} \to \mathbb{Q}^c\) que sea una inyección.
   d) ¿Qué podemos concluir ahora usando el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein?
10. Dejar\(J\) ser el intervalo de apertura de la unidad. Es decir,\(J = \{x \in \mathbb{R}\ |\ 0 < x < 1\}\) y vamos\(S = \{(x, y) \in \mathbb{R} \times \mathbb{R} \ |\ 0 < x < 1 \text{ and } 0 < y <1\}\). Llamamos a\(S\) la unidad plaza abierta. Ahora vamos a definir una función\(f\) de\(S\) a\(J\). Dejar\((a, b) \in S\) y escribir las expansiones decimales de\(a\) y\(b\) en forma normalizada como Luego
    \[\begin{array} {rcl} {a} &= & {0.a_{1}a_{2}a_{3}a_{4} \cdot\cdot\cdot a_{n} \cdot\cdot\cdot } \\ {b} &= & {0.b_{1}b_{2}b_{3}b_{4} \cdot\cdot\cdot b_{n} \cdot\cdot\cdot .} \end{array}\]
    definimos\(f(a, b) = 0.a_{1}b_{1}a_{2}b_{2}a_{3}b_{3}a_{4}b_{4} \cdot\cdot\cdot a_{n}b_{n} \cdot\cdot\cdot .\)
    
    (a) Determinar los valores de\(f(0.3, 0.625)\),\(f(\dfrac{1}{3}, \dfrac{1}{4})\), y\(f(\dfrac{1}{6}, \dfrac{5}{6})\).
    b) Si es posible, encontrar\((x, y) \in S\) tal que\(f(x, y) = 0.2345\).
    c) De ser posible, encontrar\((x, y) \in S\) tal que\(f(x, y) = \dfrac{1}{3}\).
    d) De ser posible, encontrar\((x, y) \in S\) tal que\(f(x, y) = \dfrac{1}{2}\).
    (e) Explicar por qué la función\(f: S \to J\) es una inyección pero no es una sobreyección.
    f) Utilizar el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein para demostrar que la cardinalidad de la unidad cuadrada abierta\(S\) es igual a\(c\). Si este resultado te parece sorprendente, estás en buena compañía. En una carta escrita en 1877 al matemático Richard Dedekind describiendo este resultado que había descubierto, Georg Cantor escribió: “Lo veo pero no lo creo”.
    
    Exploraciones y actividades
11. El Intervalo Cerrado [0,1]. En el Ejercicio (6) se utilizó el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein para demostrar que el intervalo cerrado [0, 1] tiene cardinalidad\(c\). Esto puede parecer un poco insatisfactorio ya que no hemos probado el Teorema de Cantor-Schr\(\ddot{o}\) der-Bernstein. En esta actividad, probaremos esa tarjeta\(([0, 1]) = c\) mediante el uso de bijecciones apropiadas.
    
    (a) Que\(f:[0, 1] \to [0, 1)\) por
    \[f(x) = \begin{cases} \dfrac{1}{2} & \text{ if \(x = 0\)} \\ \dfrac{1}{n + 1} & \text{ if \(x = \dfrac{1}{2}\) for some \(n \in \mathbb{N}\)} \\ x & \text{otherwise.} \end{cases}\]
    i. Determine\(f(0)\),\(f(1)\),\(f(\dfrac{1}{2})\),\(f(\dfrac{1}{3})\),\(f(\dfrac{1}{4})\), y\(f(\dfrac{1}{5})\).
    ii. Haga un boceto de una gráfica de la función\(f\). Pista: Comience con la gráfica de\(y = x\) for\(0 \le x \le 1\). Desmonte el punto (1, 1) y sustitúyalo por el punto (1,\(\dfrac{1}{2}\)). A continuación, retire el punto\((\dfrac{1}{2}, \dfrac{1}{2})\) y reemplácelo por el punto\((\dfrac{1}{2}, \dfrac{1}{3})\). Continuar con este proceso de eliminación de puntos en la gráfica de\(y = x\) y sustituirlos por los puntos determinados a partir de la información de la Parte (11 (a) i). Detente después de repetir esto cuatro o cinco veces para que el patrón de este proceso se haga evidente.
    iii. Explicar por qué la función\(f\) es una biyección.
    iv. \([0, 1] \thickapprox [0, 1)\)Demuéstralo.

    (b) Dejar\(g: [0, 1) \to (0, 1)\) por
    \[g(x) = \begin{cases} \dfrac{1}{n + 1} & \text{ if \(x = \dfrac{1}{2}\) for some \(n \in \mathbb{N}\)} \\ x & \text{otherwise.} \end{cases}\]
    i. Seguir el procedimiento sugerido en la Parte (11a) para esbozar una gráfica de\(g\).
    ii. Explicar por qué la función\(g\) es una biyección.
    iii. \([0, 1) \thickapprox (0, 1)\)Demuéstralo.
    c) Demostrar que [0, 1] y [0, 1) son ambos incontables y tienen cardinalidad\(c\).

Contestar

Agrega textos aquí. No elimine primero este texto.

---