7.4: El álgebra de combinaciones
- Page ID
- 113975
Anteriormente en este capítulo determinamos el número de\(k\) -subconjuntos de un conjunto de tamaños\(n\). Estos números, denotados por\(C(n, k) = nCk = \binom{n}{k}\) y determinados por la fórmula\(\dfrac{n!}{k!(n−k)!}\) se conocen como coeficientes binomiales. Parece probable que ya hayas visto la disposición de estos coeficientes binomiales en una matriz triangular —conocida como triángulo de Pascal, pero si no...
\(1\)
\(1\;\; 1\)
\(1\;\; 2 \;\;1\)
\(1 \;\;3\;\; 3 \;\;1\)
\(1\;\; 4 \;\;6 \;\;4\;\; 1\)
\(1\;\; 5 \;\;10 \;\;10\;\; 5\;\; 1\)
\(1\;\; 6\;\; 15 \;\;20\;\; 15 \;\;6\;\;1\)
etcétera.
Lo que hace que este triángulo sea tan agradable y que lleva al extraño nombre de “coeficientes binomiales” para el número de\(k\) -combinaciones de un\(n\) -set es que puedes usar el triángulo para (muy rápidamente) calcular potencias de binomios.
Un binomio es un polinomio con dos términos. Cosas como\((x + y)\),\((x + 1)\) y\((x^7 + x^3)\) todas cuentan como binomios pero para mantener las cosas simples solo piénsalo\((x + y)\). Si necesitas calcular una gran potencia de solo\((x + y)\) puedes multiplicarla, por ejemplo, piensa en encontrar el\(6^{\text{th}}\) poder de\((x + y)\).
Podemos usar la regla F.O.I.L para encontrar\((x + y)^2 = x^2 + 2xy + y^2\). Entonces\((x + y)^3 = (x + y) · (x + y)^2 = (x + y) · (x^2 + 2xy + y^2)\).
Puedes calcular ese último producto ya sea usando la ley distributiva o el método de tabla
| \(x^2 +2xy +y^2\) | ||
| \(x\) | ||
| \(+y\) | ||
De cualquier manera, la respuesta debería ser\((x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3\).
Por último, el sexto poder es el cuadrado del cubo así
\((x + y)^6 = (x + y)^3 · (x + y)^3 = (x^3 + 3x^2y + 3xy^2 + y^3) · (x^3 + 3x^2 y + 3xy^2 + y^3 )\)
Para este producto ni siquiera pensaría en la ley distributiva, saltaría al método de la mesa de inmediato:
| \(x^3\) | \(+3x^2 y\) | \(+3xy^2\) | \(+y^3\) | |
| \(x^3\) | ||||
| \(+3x^2 y\) | ||||
| \(+3xy^2\) | ||||
| \(+y^3\) | ||||
Al final, debes obtener
\(x^6 + 6x^5 y + 15x^4 y^2 + 20x^3 y^3 + 15x^2 y^4 + 6xy^5 + y^6\).
Ahora todo esto es mucho trabajo y realmente es mucho más fácil notar la forma de la respuesta: El exponente encendido\(x\) comienza en\(6\) y desciende con cada término sucesivo hasta\(0\). El exponente encendido\(y\) comienza en\(0\) y asciende a\(6\). Los coeficientes en la respuesta son los números en la sexta fila del triángulo de Pascal.
Por último, la forma del triángulo de Pascal hace que sea realmente fácil de extender. Un número en el interior del triángulo es siempre la suma de los dos por encima de él (a cada lado). Los números que no están en el interior del triángulo son siempre\(1\).
Mostramos filas\(0\) a través de\(6\) arriba. Filas\(7\) y\(8\) son
\(1\;\; 7 \;\;21\;\; 35\;\; 35\;\; 21 \;\;7 \;\;1\)
\(1\;\; 8 \;\;28\;\; 56\;\; 70\;\; 56\;\; 28\;\; 8\;\; 1.\)
Con esta información en la mano, se convierte en nada más que una cuestión de copiar la respuesta para calcular
\((x+y)^8 = x^8+8x^7 y+28x^6 y^2+56x^5 y^3+70x^4 y^4+56x^3 y^5+28x^2 y^6+8xy^7+y^8 .\)
Dado el método que utiliza el triángulo de Pascal para calcular\((x + y)\) n, podemos usar la sustitución para determinar potencias binomiales más generales. Encuentra\((x^4 + x^2 )^5\).
Todo lo anterior depende de que se puede calcular un coeficiente binomial sumando los dos que aparecen a cada lado y por encima de él en el triángulo de Pascal. Este hecho es la relación fundamental entre los coeficientes binomiales —suele llamarse la fórmula de Pascal.
Para todos los números naturales\(n\) y\(k\) con\(0 < k ≤ n\),
\[\binom{n}{k} = \binom{n − 1}{k} + \binom{n − 1}{k − 1}. \]
Vamos a demostrarlo dos veces.
- Prueba #1
-
(La primera prueba es un argumento combinatorio).
Hay\(\binom{n}{k}\) subconjuntos de tamaño\(k\) del conjunto\(N = \{1, 2, 3, . . . , n\}\). Particionaremos estos\(k\) -subconjuntos en dos casos disjuntos: los que contienen el número final\(n\),, y los que no. Let
\[A = \{S ⊆ N |S| = k ∧ n \notin S\}\]
y, vamos
\[B = \{S ⊆ N |S| = k ∧ n ∈ S\}\]
Dado que el número\(n\) está en un\(k\) -subconjunto o no lo está, estos conjuntos son disjuntos y exhaustivos. Entonces la regla de la suma nos dice que
\[\binom{n}{k} = |A| + |B|.\]
El conjunto\(A\) es realmente solo el conjunto de todos los\(k\) -subconjuntos del\((n − 1)\) -set\(\{1, 2, 3, . . . , n − 1\}\), entonces\(|A| = \binom{n−1}{k}\).
Cualquiera de los conjuntos en se\(B\) puede obtener al unir el elemento\(n\) a un\(k−1\) subconjunto del\((n−1)\) -set\(\{1, 2, 3, . . . , n−1\}\), así que\(|B| = \binom{n−1}{k−1}\).
La sustitución nos da el resultado deseado.
Q.E.D
- Prueba #2
-
(La segunda prueba es de naturaleza algebraica.)
Considera la suma
\[ \binom{n-1}{k} + \binom{n − 1}{k − 1}.\]
Aplicando la fórmula que deducimos en la Sección 7 obtenemos
\[\begin{array} s \binom{n − 1}{k} + \binom{n − 1}{k − 1} &= \dfrac{(n − 1)!}{k!(n − 1 − k)!} + \dfrac{(n − 1)!}{(k − 1)!((n − 1) − (k − 1))!} \\ &= \dfrac{(n − 1)!}{k!(n − k − 1)!} + \dfrac{(n − 1)!}{(k − 1)!(n − k)!} \end{array}\]
Un denominador común para estas fracciones es\(k!(n − k)!\). (Tendremos que multiplicar la parte superior e inferior de la primera fracción por\((n − k)\) y la parte superior e inferior de la segunda fracción por\(k\).)
\[\begin{array} &&= \dfrac{(n − k)(n − 1)!}{k!(n − k)(n − k − 1)!} + \dfrac{k(n − 1)!}{k(k − 1)!(n − k)!} \\ &= \dfrac{(n − k)(n − 1)!}{k!(n − k)!} + \dfrac{k(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n − k)(n − 1)! + k(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n − k + k)(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n)(n − 1)!}{k!(n − k)!} \\ &= \dfrac{n!}{k!(n − k)!} \end{array}.\]
Reconocemos la expresión final como la definición de\(\binom{n}{k}\), por lo que hemos demostrado que
\[\binom{n − 1}{k} + \binom{n − 1}{k − 1} = \binom{n}{k}.\]
Q.E.D
Hay bastantes otras identidades concernientes al coeficiente binomial que también se pueden probar en (al menos) dos formas. Te proporcionaremos uno o dos ejemplos más y te dejaremos el resto en los ejercicios para esta sección.
Para todos los números naturales\(n\) y\(k\) con\(0 < k ≤ n\),
\[ k · \binom{n}{k} = n · \binom{n − 1}{k − 1}.\]
Probemos primero un enfoque puramente algebraico.
- Prueba
-
Usando la fórmula para el valor de un coeficiente binomial obtenemos
\[k · \binom{n}{k} = k · \binom{n!}{k!(n − k)!}.\]
Podemos hacer alguna cancelación para obtener
\[k · \binom{n}{k} = \binom{n!}{(k − 1)!(n − k)!}.\]
Finalmente factorizamos un\(n\) para obtener
\[k · \binom{n}{k} = n · \binom{(n − 1)!}{(k − 1)!(n − k)!},\]
ya que\((n − k)\) es lo mismo\(((n − 1) − (k − 1))\) que tenemos
\[k · \binom{n}{k} = n · \binom{(n − 1)!}{(k − 1)!((n − 1) − (k − 1))!} = n · \binom{n − 1}{k − 1} \]
Q.E.D.
Un argumento combinatorio suele implicar contar algo de dos maneras. ¿Qué podría ser ese algo? Bueno, si ves un producto en alguna fórmula deberías tratar de imaginar lo que diría la regla de multiplicación en esa circunstancia particular.
- Prueba
-
Considera la colección de todos los subconjuntos de tamaño\(k\) tomados\(N = \{1, 2, 3, . . . , n\}\) de los que se ha marcado uno de los elementos para distinguirlo de los demás de alguna manera. 1
Podemos contar esta colección de dos maneras usando la regla de multiplicación.
En primer lugar, podríamos seleccionar un\(k\) -subconjunto de\(\binom{n}{k}\) maneras y luego de entre los\(k\) elementos del subconjunto podríamos seleccionar uno para ser marcado. Por este análisis, hay\(\binom{n}{k} · k\) elementos en nuestra colección.
En segundo lugar, podríamos seleccionar un elemento del\(n\) -set que será el elemento “marked” de nuestro subconjunto, y luego elegir los\(k − 1\) elementos adicionales de los\(n − 1\) elementos restantes del\(n\) -set. Por este análisis hay\(n· \binom{n−1}{k−1}\) elementos en la colección que hemos estado discutiendo.
Por lo tanto,
\[k · \binom{n}{k} = n · \binom{n − 1}{k − 1}\]
Q.E.D.
El resultado final del que hablaremos en realidad tiene (al menos) tres pruebas. Uno de los cuales sufre la falla de que es “como aplastar una mosca con un martillo”.
El resultado se refiere a la suma de todos los números en alguna fila del triángulo de Pascal.
Para todos los números naturales\(n\) y\(k\) con\(0 < k ≤ n\),
\[\sum_{k=0}^{n} \binom{n}{k} = 2^n\]
Nuestro mazo es un poderoso resultado conocido como el teorema binomial que es una declaración formalizada del material con el que iniciamos esta sección.
Para todos los números naturales\(n\), y números reales\(x\) y\(y\),
\[(x + y)^n = \sum_{k=0}^{n} \binom{n}{k} = x^{n−k} y^k\]
- Prueba
-
No vamos a estar demostrando este resultado en este momento. Pero, la siguiente prueba es una prueba del teorema anterior utilizando este resultado más poderoso.
- Prueba #1 (del teorema\(7.4.3\))
-
Sustituto\(x = y = 1\) en el teorema binomial.
Q.E.D.
Nuestra segunda prueba será combinatoria. Reiteremos que una prueba combinatoria suele consistir en contar alguna colección de dos maneras diferentes. La fórmula que tenemos en este ejemplo contiene una suma, por lo que debemos buscar una colección de cosas que se puedan contar usando la regla de suma.
- Prueba #2 (del teorema\(7.4.3\))
-
El conjunto de todos los subconjuntos de\(N = \{1, 2, 3, . . . , n\}\), que denotamos por\(\mathcal{P}(N)\), se puede dividir en\(n + 1\) conjuntos basados en los tamaños de los subconjuntos,
\[\mathcal{P}(N) = S_0 ∪ S_1 ∪ S_2 ∪ . . . ∪ S_n,\]
donde\(S_k = \{S | S ⊆ N ∧ |S| = k\}\) para\(0 ≤ k ≤ n\). Dado que ningún subconjunto de\(N\) puede aparecer en dos partes diferentes de la partición (el tamaño de un subconjunto es único) y cada subconjunto de\(N\) aparece en una de las partes de la partición (los tamaños de los subconjuntos están todos en el rango de\(0\) a\(n\)). El principio de adición nos dice que
\[|\mathcal{P}(N)| = |S_0| + |S_1| + ∪|S_2| + . . . + |S_n|.\]
Anteriormente lo hemos demostrado\(|\mathcal{P}(N)| = 2^n\) y sabemos que\(|S_k| = \binom{n}{k}\) así se deduce que
\[2^n = \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + . . . + \binom{n}{n}\]
Q.E.D.
Ejercicios:
Utilice el teorema binomial (con\(x = 1000\) y\(y = 1\)) para calcular\(1001^6\).
Encuentra\((2x + 3)^5\)
Encuentra\((x^2 + y^2 )^6\).
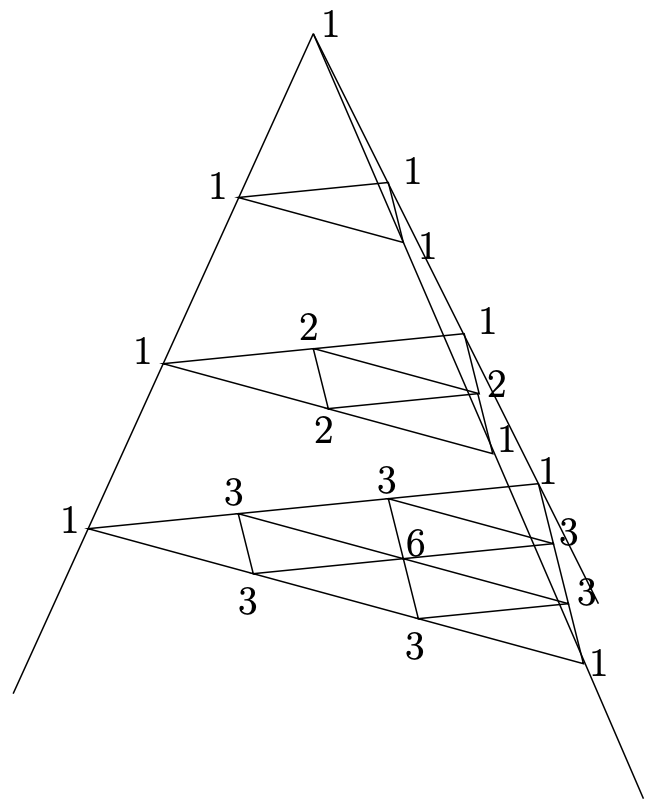
El siguiente diagrama contiene un análogo\(3\) -dimensional del triángulo de Pascal que podríamos llamar “tetraedro de Pascal”. ¿Cómo sería la siguiente capa?
El gobierno estudiantil en Lagrange High está formado por\(24\) miembros elegidos entre el cuerpo estudiantil general de\(210\). Adicionalmente, hay un comité directivo de\(5\) miembros elegidos entre los miembros del gobierno estudiantil. Utilice la regla de multiplicación para determinar dos fórmulas diferentes para el número total de estructuras de gobierno posibles.
Demostrar la identidad
\(\binom{n}{k} · \binom{k}{r} = \binom{n}{r} · \binom{n − r}{k − r} \)
combinatorialmente.
Demostrar el teorema binomial.
\(∀n ∈ \mathbb{N}, ∀_{x, y} ∈ \mathbb{R}, (x + y)^n = \sum^{n}_{k=0} \binom{n}{k} x^{n−k} y^k\)


