5.1: Límites

La idea de un límite es la piedra angular del cálculo. Es algo sutil, razón por la cual, aunque estaba implícita en la obra de Arquímedes\(^{1}\), y esencial para una adecuada comprensión de las paradojas de Zenón, tardó dos mil años en comprenderse plenamente. El cálculo fue desarrollado en el\(17^{\text {th }}\) siglo por Newton y Leibniz con un enfoque algo arrogante de los límites; no fue sino hasta el\(19^{\text {th }}\) siglo que se le dio una definición rigurosa de límite, por Cauchy.

En Sección\(5.1\) definimos límites, y probamos algunas propiedades elementales. En Sección\(5.2\) discutimos funciones continuas, y en Sección\(5.3\) analizamos los límites de secuencias de funciones.

Límites

Dada una función real\(f: X \rightarrow \mathbb{R}\), la idea intuitiva del enunciado\[\lim _{x \rightarrow a} f(x)=L\] es que, a medida que\(x\) se acerca cada vez más\(a\), los valores de\(f(x)\) acercarse cada vez más\(L\). Hacer esta noción precisa no es fácil: intenta escribir una definición matemática ahora, antes de seguir leyendo.

La idea detrás de la definición es dar una secuencia de garantías. Imagínate como abogado, tratando de defender el reclamo (5.1). Por concreción, arreglemos\(g(x)=\frac{\sin (x)}{x}\), e intentemos defender la afirmación de que\[\lim _{x \rightarrow 0} g(x)=1\]\({ }^{1}\) Arquímedes (287-212 a.C.) calculó el área bajo una parábola (lo que ahora llamaríamos\(\int_{0}^{1} x^{2} d x\)) calculando el área de los rectángulos de ancho \(1 / N\)bajo la parábola y dejando\(N\) tender al infinito. Esto es idéntico al enfoque moderno de encontrar una integral tomando un límite de sumas de Riemann.

FIGURA 5.3. Parcela de\(\sin (x) / x\)

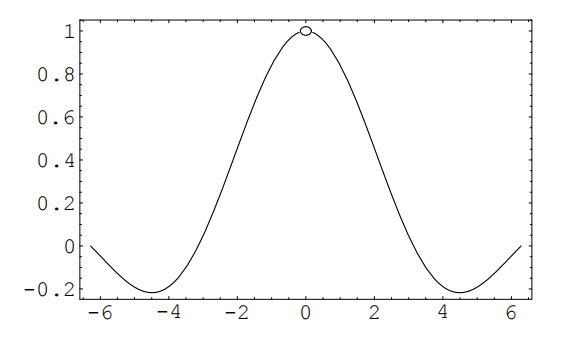
El juez escéptico pregunta “¿Se puede garantizar que\(g(x)\) está dentro de .1 de 1?”

“Sí, señoría, siempre que eso”\(|x|<.7\).

“Mmm, bueno, ¿puedes garantizar que\(g(x)\) está dentro\(.01\) de 1?”

“Sí, señoría, siempre que\(|x|<.2 . "\)

Y así va. Si, por cada tolerancia posible que plantea el juez, puede encontrar una precisión (es decir, una desviación permisible\(x\) de\(a\)) que garantice que la diferencia entre el valor de la función y el límite está dentro de la tolerancia permisible, entonces puede defender con éxito el Reclamación.

EJERCICIO. Ahora trata de dar una definición matemática de un límite, sin leer más.

Comenzaremos con el caso de que la función se defina en un intervalo abierto.

DEFINICIÓN. Limit,\(\lim _{x \rightarrow a} f(x)\) Let\(I\) be an open interval and\(a\) some point in\(I\). Dejar\(f\) ser una función de valor real definida en\(I \backslash\{a\}\). (No importa si\(f\) se define en\(a\) o no). Entonces decimos\[\lim _{x \rightarrow a} f(x)=L\] (en palabras, “el límite como\(x\) tiende a\(a\) de\(f(x)\) es\(L\) “) si, por cada\(\varepsilon>0\), existe\(\delta>0\), de manera que\[0<|x-a|<\delta \quad \Longrightarrow \quad|f(x)-L|<\varepsilon\]

FIGURA 5.5. Una opción\(\delta\) para un determinado\(\varepsilon\)

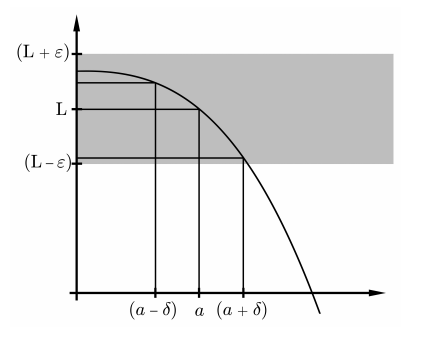
La condición\(0<|x-a|<\delta\) significa que excluimos\(x=a\) de la consideración. Los límites son sobre el comportamiento de una función cerca del punto, no en el punto. Para una función como\(g(x)=\sin (x) / x\), el valor en 0 no está definido; sin embargo\(\lim _{x \rightarrow 0} g(x)\) existe, y es el mismo que el\(\lim _{x \rightarrow 0}\) de la función\[h(x)=\left\{\begin{array}{cc} \sin (x) / x & x \neq 0 \\ 5 & x=0 . \end{array}\right.\] REMARK. El uso de\(\varepsilon\) para el error permisible y\(\delta\) para la precisión correspondiente requerida se santifica por el uso prolongado. Los matemáticos necesitan todos los símbolos convenientes que puedan encontrar. El alfabeto griego se ha utilizado durante mucho tiempo como un suplemento del alfabeto romano en las matemáticas occidentales, y hay que estar familiarizado con él (ver Apéndice A para el alfabeto griego). El punto principal a tener en cuenta en la definición es el orden de los cuantificadores:\(\forall \varepsilon, \exists \delta\). Qué significaría decir\[(\exists \delta>0)(\forall \varepsilon>0) \quad[0<|x-a|<\delta \quad \Longrightarrow \quad|f(x)-L|<\varepsilon] ?\] Hablar cómodamente de límites, ayuda tener algunas palabras que describan las desigualdades (5.4). Digamos que el\(\varepsilon\) -vecindario de\(L\) es el conjunto de puntos dentro\(\varepsilon\) de\(L\), es decir, el intervalo\((L-\varepsilon, L+\varepsilon)\). El\(\delta\) barrio perforado de\(a\) es el conjunto de puntos dentro\(\delta\) de\(a\), excluyéndose a\(a\) sí mismo, es decir\((a-\delta, a) \cup(a, a+\delta)\). Cuando hablamos de\(\varepsilon\) -barrios y barrios perforados\(\delta\) -, siempre asumimos eso\(\varepsilon\) y\(\delta\) somos positivos, para que los barrios no estén vacíos.

Entonces la definición de límite se puede redactar como “cada\(\varepsilon\) -barrio de\(L\) tiene una imagen inversa debajo\(f\) que contiene algún\(\delta\) barrio perforado de\(a\)”.

OBSERVACIÓN. Podemos revisar nuestra analogía de sala de audiencias, y decir que para demostrar que\(f\) tiene límite\(L\) en\(a\), necesitamos una estrategia que produzca un viable\(\delta\) para cualquier\(\varepsilon\). Entonces una prueba es esencialmente una función\(F\) que toma cualquier positivo\(\varepsilon\) y escupe un positivo\(\delta=F(\varepsilon)\) para el cual (5.4) funciona.

EJEMPLO 5.6. Vamos\(f(x)=5 x+2\). Demostrar\(\lim _{x \rightarrow 3} f(x)=17\).

Vamos\(\varepsilon>0\). Queremos encontrar un para\(\delta>0\) que el\(\delta\) barrio perforado de 3 se mapee en el\(\varepsilon\) -barrio de 17.

FIGURA 5.7. Relación entre\(\delta\) y\(\varepsilon\)

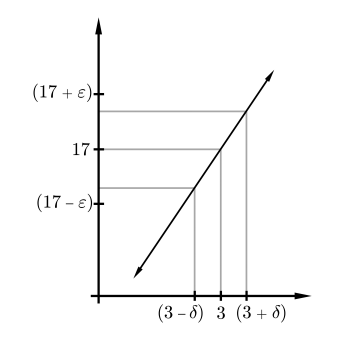
Tomar\(\delta=\varepsilon / 5\) funcionará, al igual que cualquier elección más pequeña de\(\delta\). En efecto, si\(0<|x-3|<\delta\), entonces\(|f(x)-17|<5 \delta=\varepsilon\).

EJEMPLO 5.8. Esta vez, vamos\(g(x)=55 x+2\). Para probar\(\lim _{x \rightarrow 3} g(x)=\) 167, debemos tomar\(\delta \leq \varepsilon / 55\).

Si dos funciones\(f\) y\(g\) ambas tienen límites en el punto\(a\), entonces también lo hacen todas las combinaciones algebraicas\(f+g, f-g, f \cdot g\) y\(c f\) para\(c\) una constante. El cociente\(f / g\) también tiene un límite en\(a\), siempre y cuando\(\lim _{x \rightarrow a} g(x) \neq 0\). Además, estos límites son lo que cabría esperar.

TEOREMA 5.9. Supongamos\(f\) y\(g\) son funciones en un intervalo abierto\(I\), y en el punto\(a\) en\(I\) ambos\(\lim _{x \rightarrow a} f(x)\) y\(\lim _{x \rightarrow a} g(x)\) existir. \(c\)Sea cualquier número real. Después\[\begin{aligned} \text { (i) } \lim _{x \rightarrow a}[f(x)+g(x)] &=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x) \\ \text { (ii) } \lim _{x \rightarrow a}[f(x)-g(x)] &=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a} g(x) \\ \text { (iii) } \quad \lim _{x \rightarrow a} c f(x) &=c\left[\lim _{x \rightarrow a} f(x)\right] \\ (i v) \quad \lim _{x \rightarrow a}[f(x) g(x)] &=\left[\lim _{x \rightarrow a} f(x)\right] \cdot\left[\lim _{x \rightarrow a} g(x)\right] \\ \text { (v) } \quad \lim _{x \rightarrow a} \frac{f(x)}{g(x)} &=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}, \quad \text { provided } \lim _{x \rightarrow a} g(x) \neq 0 . \end{aligned}\] Discusión. ¿Cómo vamos a probar un teorema así? Bueno, para empezar, no se deje intimidar por su longitud. Empecemos por la parte (i). Solo tenemos la definición de límite para trabajar, por lo que solo tenemos una opción estratégica: demostrar directamente que la definición está satisfecha.

COMPROBACIÓN DE (i). Dejar\(L_{1}\) y\(L_{2}\) ser los límites de\(f\) y\(g\) respectivamente en\(a\). Dejar\(\varepsilon\) ser un número positivo arbitrario. Debemos encontrar un\(\delta>0\) modo que\[0<|x-a|<\delta \quad \Longrightarrow \quad\left|f(x)+g(x)-\left(L_{1}+L_{2}\right)\right|<\varepsilon .\] La idea clave, común a muchos argumentos de límite, es utilizar la observación de que Se\[\left|f(x)+g(x)-\left(L_{1}+L_{2}\right)\right| \leq\left|f(x)-L_{1}\right|+\left|g(x)-L_{2}\right| .\] trata de una aplicación de la llamada desigualdad triangular, que se le pide después que demuestre (Lema 5.14). Es la aseveración que para cualquier número real\(c\) y\(d\), tenemos\[|c+d| \leq|c|+|d| .\] (¿Qué valores de\(c\) y\(d\) rendimiento (5.10)?) Entonces, si podemos hacer ambos\(\left|f(x)-L_{1}\right|\) y\(\left|g(x)-L_{2}\right|\) pequeños, entonces Desigualdad (5.10) obliga\[\left|f(x)+g(x)-\left(L_{1}+L_{2}\right)\right|\] a ser pequeños también, que es lo que queremos.

Desde\(f\) y\(g\) tener límites\(L_{1}\) y\(L_{2}\) en\(a\), sabemos que existen números positivos\(\delta_{1}\) y\(\delta_{2}\) tal que\[\begin{array}{lll} 0<|x-a|<\delta_{1} & \Longrightarrow & \left|f(x)-L_{1}\right|<\varepsilon \\ 0<|x-a|<\delta_{2} & \Longrightarrow & \left|g(x)-L_{2}\right|<\varepsilon \end{array}\] si\(|x-a|\) es menor que ambos\(\delta_{1}\) y\(\delta_{2}\), entonces ambas desigualdades están satisfechas, y obtenemos\[\left|f(x)+g(x)-\left(L_{1}+L_{2}\right)\right| \leq\left|f(x)-L_{1}\right|+\left|g(x)-L_{2}\right| \leq \varepsilon+\varepsilon .\] Esto no es lo suficientemente bueno; queremos que el lado izquierdo de (5.11) quede delimitado por\(\varepsilon\), no\(2 \varepsilon\). Estamos salvados, sin embargo, por el requisito de que para cualquier número positivo\(\eta\), podamos garantizar eso\(f\) y\(g\) estamos en un\(\eta\) -barrio de\(L_{1}\) y\(L_{2}\), respectivamente. En particular,\(\eta\) dejémoslo\(\varepsilon / 2\). Desde\(f\) y\(g\) tener límites en\(a\), hay números positivos\(\delta_{3}\) y\(\delta_{4}\) así que\[\begin{array}{lll} 0<|x-a|<\delta_{3} & \Longrightarrow & \left|f(x)-L_{1}\right|<\frac{\varepsilon}{2} \\ 0<|x-a|<\delta_{4} & \Longrightarrow & \left|g(x)-L_{2}\right|<\frac{\varepsilon}{2} . \end{array}\] Así que establecemos\(\delta\) iguales a los más pequeños de\(\delta_{3}\) y \(\delta_{4}\), y obtenemos\[\begin{aligned} &0<|x-a|<\delta \Longrightarrow \\ &\quad\left|f(x)+g(x)-\left(L_{1}+L_{2}\right)\right| \leq\left|f(x)-L_{1}\right|+\left|g(x)-L_{2}\right|<\varepsilon, \end{aligned}\] según sea necesario. EJERCICIO. Explique con palabras cómo funcionaba la prueba anterior. En mano corta, se podría decir que si\(F_{1}\) y\(F_{2}\) son estrategias para probar\(\lim _{x \rightarrow a} f(x)=L_{1}\) y\(\lim _{x \rightarrow a} g(x)=L_{2}\) respectivamente, entonces\[F=\min \left\{F_{1}\left(\frac{\varepsilon}{2}\right), F_{2}\left(\frac{\varepsilon}{2}\right)\right\}\] es una estrategia para probar\(\lim _{x \rightarrow a} f(x)+g(x)=L_{1}+L_{2}\).

Discusión. ¿Qué sigue? Podríamos probar (ii) de manera similar, pero a los matemáticos les gustan los atajos. Observe que si probamos (iii) y dejamos\(c=-1\), entonces podemos aplicar (i)\(f+(-g)\) y obtener (ii) de esa manera. Además, (iii) es solo un caso especial de (iv), si sabemos que la función constante\(g(x)=c\) tiene el límite\(c\) en cada punto. Entonces probemos (iv) siguiente.

COMPROBACIÓN DE (iv). Nuevamente, dejemos\(\varepsilon\) ser un número positivo arbitrario. Debemos encontrar una\(\delta>0\) para que no\[0<|x-a|<\delta \quad \Longrightarrow \quad\left|f(x) g(x)-\left(L_{1} L_{2}\right)\right|<\varepsilon .\] quede muy claro qué tan cerca\(f\) y\(g\) tiene que estar de\(L_{1}\) y\(L_{2}\) para conseguir que su producto esté lo suficientemente cerca de\(L_{1} L_{2}\), así que vamos a jugarlo seguro al no elegir todavía. Por cada\(\varepsilon_{1}, \varepsilon_{2}>0\), sabemos que existe\(\delta_{1}, \delta_{2}>0\) tal que\[\begin{array}{lll} 0<|x-a|<\delta_{1} & \Longrightarrow & \left|f(x)-L_{1}\right|<\varepsilon_{1} \\ 0<|x-a|<\delta_{2} & \Longrightarrow & \left|g(x)-L_{2}\right|<\varepsilon_{2} \end{array}\] Ahora usamos el segundo truco común para probar la existencia de límites: sumar y restar la misma cantidad para que uno pueda factorizar. \[\begin{aligned} \left|f(x) g(x)-L_{1} L_{2}\right| &=\left|f(x) g(x)-L_{1} g(x)+L_{1} g(x)-L_{1} L_{2}\right| \\ & \leq\left|f(x) g(x)-L_{1} g(x)\right|+\left|L_{1} g(x)-L_{1} L_{2}\right| \\ & \leq\left|f(x)-L_{1}\right||g(x)|+\left|g(x)-L_{2}\right|\left|L_{1}\right| \cdot \quad(5.1 \end{aligned}\]Ahora bien, si ambos summands en la última línea se pueden hacer menos que\(\varepsilon / 2\), ganamos. El segundo término es fácil: elegimos\[\varepsilon_{2}=\frac{\varepsilon}{2\left|L_{1}\right|+1} .\] Luego hay un\(\delta_{2}\) modo que\[\begin{aligned} 0<|x-a|<\delta_{2} & \Longrightarrow \quad\left|g(x)-L_{2}\right| &<\varepsilon_{2} \\ & \Longrightarrow \quad\left|g(x)-L_{2}\right|\left|L_{1}\right| &<\frac{\varepsilon\left|L_{1}\right|}{2\left|L_{1}\right|+1}<\frac{\varepsilon}{2} \end{aligned}\] (Si\(L_{1} \neq 0\), podríamos haber elegido\(\varepsilon_{2}=\frac{\varepsilon}{2\left|L_{1}\right|}\); agregamos 1 al denominador solo para que no tuviéramos que considerar los dos casos por separado.)

¿Y el primer summand en (5.12), el término\(\left|f(x)-L_{1}\right||g(x)|\)? Primero vamos a ponernos un poco atados sobre lo grande que\(|g|\) puede ser. Sabemos que si\(0<|x-a|<\delta_{2}\), entonces\(\left|g(x)-L_{2}\right|<\varepsilon /\left(2\left|L_{1}\right|+1\right)\), entonces\[|g(x)|<\left|L_{2}\right|+\frac{\varepsilon}{2\left|L_{1}\right|+1}=: M .\] Si lo dejamos\(\varepsilon_{1}=\varepsilon /(2 M)\), sabemos que existe\(\delta_{1}>0\) para que\[0<|x-a|<\delta_{1} \quad \Longrightarrow \quad\left|f(x)-L_{1}\right||g(x)|<\varepsilon_{1}|g(x)| .\] Finalmente, dejamos\(\delta=\min \left(\delta_{1}, \delta_{2}\right)\). Pues\(0<|x-a|<\delta\), ambas summands en (5.12) son menores que\(\varepsilon / 2\): la segunda suma porque\(\delta \leq \delta_{2}\), y la primera porque cuando\(0<|x-a|<\delta\), la Desigualdad\(5.13\) se fortalece a\[\left|f(x)-L_{1}\right||g(x)|<\varepsilon_{1}|g(x)|<\varepsilon_{1} M=\varepsilon / 2 .\] Por lo tanto, para \(0<|x-a|<\delta\), tenemos\(\left|f(x) g(x)-L_{1} L_{2}\right|<\varepsilon\), como se desee.

COMPROBACIÓN DE (iii). Este es un caso especial de (iv), una vez que sabemos que las funciones constantes tienen límites. Digamos esto como un lema. Dado Lema 5.15, se prueba el inciso iii), y por lo tanto también lo es (ii).

COMPROBACIÓN DE (v). Ejercicio.

LEMA 5.14. Desigualdad triangular Let\(c, d\) be números reales. Entonces\(|c+d| \leq|c|+|d| .\)

PRUEBA. Ejercicio.

LEMA 5.15. Dejar\(g(x) \equiv c\) ser la función constante c. Entonces,\[(\forall a \in \mathbb{R}) \lim _{x \rightarrow a} g(x)=c .\] PRUEBA. Ejercicio.

EJEMPLO 5.16. La función Heaviside\(H(t)\) está definida por\[H(t)= \begin{cases}0 & t<0 \\ 1 & t \geq 0\end{cases}\] Show que\(H\) no tiene límite en 0.

Discusión. Para probar que no existe un límite, debemos probar lo contrario de\(\forall \varepsilon \exists \delta\), es decir, eso\(\exists \varepsilon \nexists \delta\). Como la brecha entre la función on\([0, \infty)\) y\((-\infty, 0)\) es 1, está claro que cualquier banda de ancho\(<1\) no puede ser lo suficientemente ancha como para contener valores de\(H(t)\) for\(t\) en ambos lados de 0. Entonces elegiremos algunos\(\varepsilon<.5\), y discutiremos por contradicción.

Supongamos que el límite existe y es igual\(L\). Vamos\(\varepsilon=\frac{1}{4}\). Por hipótesis, existe\(\delta>0\) tal que\[0<|t|<\delta \Longrightarrow|H(t)-L|<\frac{1}{4} .\] Pero para\(t\) negativo, esto significa\(|L|<\frac{1}{4}\); y para\(t\) positivo, esto significa\(|L-1|<\frac{1}{4}\). Así conseguimos una contradicción.

Si la función se define en el intervalo cerrado\([c, d]\), es posible que aún queramos preguntar si tiene un valor limitante en\(c\); si es así, sin embargo, solo queremos considerar puntos cercanos\(c\) que estén en el dominio de la definición. De manera más general, nos llevan a la siguiente definición de límite restringido.

DEFINICIÓN. Límite restringido,\(\lim _{X \ni x \rightarrow a} f(x)\) Supongamos que\(f\) es una función real y\(X \subseteq \operatorname{Dom}(f)\). Vamos\(a \in \mathbb{R}\). Decimos que\(\lim _{X \ni x \rightarrow a} f(x)=L\) si\((\forall \varepsilon>0)(\exists \delta>0)(\forall x \in X) \quad[0<|x-a|<\delta] \Longrightarrow|f(x)-L|<\varepsilon .\)

Leemos "\(\lim _{X \ni x \rightarrow a} f(x)=L\)" como “el límite como\(x\) tiende al\(a\) interior\(X\) de\(f(x)\) es\(L . "\) Un caso especial importante de límites restringidos son los siguientes:

DEFINICIÓN. Límite derecho,\(\lim _{x \rightarrow a^{+}} f(x)\) Let\(a, b, L \in \mathbb{R}, a<b\) y\(f\) ser una función real definida en\((a, b)\). Decimos que\[\lim _{x \rightarrow a^{+}} f(x)=L\] si\[(\forall \varepsilon>0)(\exists \delta>0)[x \in(a, a+\delta)] \Rightarrow[|f(x)-L|<\varepsilon]\] El número\(L\) es el límite de la derecha de\(f(x)\) at\(a\). El límite de la izquierda se define de manera similar. Si\(a, c, L \in \mathbb{R}, c<a\) y\(f\) es una función real definida en\((c, a)\), decimos que\(\lim _{x \rightarrow a^{-}} f(x)=L\) si los límites de la\[(\forall \varepsilon>0)(\exists \delta>0)[x \in(a-\delta, a)] \Rightarrow[|f(x)-L|<\varepsilon]\] mano derecha y los límites de la izquierda se denominan límites unilaterales. Los límites unilaterales son ejemplos de límites restringidos.

EJEMPLO 5.17. \(H(t)\)Sea la función Heaviside. Entonces\[\begin{aligned} &\lim _{t \rightarrow 0^{+}} H(t)=1 \\ &\lim _{t \rightarrow 0^{-}} H(t)=0 \end{aligned}\]