8.1: Introducción a las funciones

En este capítulo, introduciremos el concepto de función como un tipo especial de relación. Nuestra definición debe estar de acuerdo con cualquier definición previa de función que pueda haber aprendido. También estudiaremos diversas propiedades que una función puede o no poseer.

Hasta este punto, es posible que solo hayas encontrado funciones como regla algebraica, por ejemplo\(f(x)=x^{2}-1\), para transformar un número real en otro. Sin embargo, podemos estudiar funciones en un contexto mucho más amplio. Los bloques de construcción básicos de una función son un primer conjunto y un segundo conjunto, digamos\(X\) y\(Y\), y una “correspondencia” que asigna cada elemento de\(X\) a exactamente un elemento de\(Y\). Echemos un vistazo a la definición real.

Definición 8.1. Dejar\(X\) y\(Y\) ser dos conjuntos no vacíos. Una función\(f\) de\(X\) a \(Y\)es una relación de\(X\) a\(Y\) tal que para cada\(x\in X\), existe una única\(y\in Y\) tal que\((x,y)\in f\). El conjunto\(X\) se llama el dominio de\(f\) y se denota por\(dom(f)\). El conjunto\(Y\) se llama codominio de\(f\) y se denota por\(codom(f)\) mientras que el subconjunto del codominio definido vía\[\range(f):= \{y\in Y\mid \mbox{there exists }x\mbox{ such that } (x,y)\in f\}\] se llama el rango de\(f\) o la imagen de \(X\)bajo\(f\).

Hay una variedad de notación y terminología asociada a las funciones. Escribiremos\(f:X\to Y\) para indicar que\(f\) es una función de\(X\) a\(Y\). Haremos uso de enunciados como “Let\(f:X\to Y\) be the function defined via...” o “Define\(f:X\to Y\) via...”, donde\(f\) se entiende como una función en la segunda sentencia. A veces se usa el mapeo de palabras (o mapa) en lugar de la función de palabra. Si\((a,b)\in f\) por una función\(f\), a menudo escribimos\(f(a)=b\) y decimos que “\(f\)mapea\(a\)\(b\)” o “\(f\)de\(a\) iguales\(b\)”. En este caso, se\(a\) puede llamar una entrada de\(f\) y es la preimagen de\(b\) bajo\(f\) mientras\(b\) se llama una salida de\(f\) y es la imagen de\(a\) debajo\(f\). Tenga en cuenta que el dominio de una función es el conjunto de entradas mientras que el rango es el conjunto de salidas para la función.

Según nuestra definición, si\(f:X\to Y\) es una función, entonces cada elemento del dominio se utiliza exactamente una vez. Sin embargo, no hay restricciones sobre si un elemento del codominio aparece alguna vez en la segunda coordenada de un par ordenado en la relación. Sin embargo, si un elemento de\(Y\) está en el rango de\(f\), puede aparecer en más de un par ordenado en la relación.

Se deduce inmediatamente de la definición de función que dos funciones son iguales si y sólo si tienen el mismo dominio, el mismo codominio, y el mismo conjunto de pares ordenados en la relación. Es decir, funciones\(f\) y\(g\) son iguales si y sólo si\(dom(f)=dom(g)\),\(codom(f)=codom(g)\), y\(f(x)=g(x)\) para todos\(x\in X\).

Dado que las funciones son tipos especiales de relaciones, podemos representarlas usando dígrafos y gráficas cuando sea práctico. Los dígrafos para funciones a menudo se denominan diagramas de función (o mapeo). Al dibujar diagramas de funciones, es una práctica estándar poner los vértices para el dominio a la izquierda y los vértices para el codominio a la derecha, de manera que todos los bordes dirigidos apunten de izquierda a derecha. También podemos dibujar una flecha adicional etiquetada por el nombre de la función del dominio al codominio.

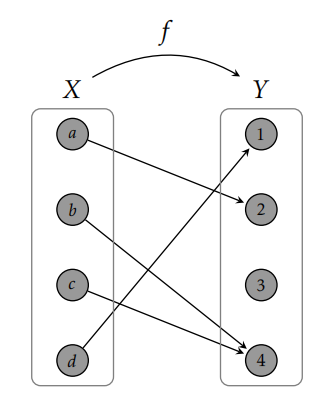
Ejemplo 8.2. Dejar\(X=\{a,b,c,d\}\)\(Y=\{1,2,3,4\}\) y definir la relación\(f\) de\(X\) a\(Y\) vía\[f=\{(a,2),(b,4),(c,4),(d,1)\}.\] Dado que cada elemento\(X\) aparece exactamente una vez como una primera coordenada,\(f\) es un función con dominio\(X\) y codominio\(Y\) (i.e.,\(f:X\to Y\)). En este caso, eso lo vemos\(\range(f)=\{1,2,4\}\). Además, podemos escribir cosas como\(f(a)=2\) y\(c\mapsto 4\), y decir cosas como “\(f\)mapas\(b\) a 4" y “la imagen de\(d\) es 1”. El diagrama de funciones para\(f\) se representa en la Figura 8.1.

Figura 8.1: Diagrama de funciones para una función de X = {a, b, c, d,} a Y = {1,2,3,4}.

Problema 8.3. Determinar si cada una de las relaciones definidas en los siguientes ejemplos y problemas es una función.

1. Ejemplo 7.3 (ver Figura 7.1)
2. Ejemplo 7.14 (ver Figura 7.3)
3. Problema 7.15
4. Problema 7.21

Problema 8.4. Dejar\(X=\{\circ, \square,\triangle, smiley\}\) y\(Y=\{a,b,c,d,e\}\). Para cada una de las siguientes relaciones, dibuje el dígrafo correspondiente y determine si la relación representa una función de\(X\)\(Y\) a\(Y\)\(X\),\(X\) a\(X\), a, o no representan una función. Si la relación es una función, determine el dominio, el codominio y el rango.

1. \(f=\{(\circ, a),(\square,b),(\triangle,c),(smiley,d)\}\)
2. \(g=\{(\circ, a),(\square,b),(\triangle,c),(smiley,c)\}\)
3. \(h=\{(\circ, a),(\square,b),(\triangle,c),(\circ,d)\}\)
4. \(k=\{(\circ, a),(\square,b),(\triangle,c),(smiley,d),(\square,e)\}\)
5. \(l=\{(\circ, e),(\square,e),(\triangle,e),(smiley,e)\}\)
6. \(m=\{(\circ, a),(\triangle,b),(smiley,c)\}\)
7. \(i=\{(\circ,\circ),(\square, \square),(\triangle,\triangle),(smiley,smiley)\}\)
8. Definir la relación\(\operatorname{happy}\) de\(Y\) a\(X\) vía\((y,smiley)\in\operatorname{happy}\) para todos\(y\in Y\).
9. \(\operatorname{nugget}=\{(\circ,\circ),(\square, \square),(\triangle,\triangle),(smiley,\square)\}\)

Las dos últimas partes del problema anterior dejan claro que las funciones pueden tener nombres consistentes en más de una letra. Los nombres de funciones\(\sin\)\(\cos\),\(\log\),, y\(\ln\) son instancias de esto que probablemente hayas encontrado en tu experiencia previa en matemáticas. Una cosa que quizás nunca hayas notado es el tipo de fuente que usamos para los nombres de funciones. Es común poner en cursiva nombres de funciones genéricos como\(f\) pero no nombres de funciones comunes como\(\sin\). Sin embargo, siempre ponemos en cursiva las variables utilizadas para representar la entrada y salida de una función. Por ejemplo, considere los tipos de fuente utilizados en las expresiones\(\sin(x)\) y\(\ln(a)\).

Problema 8.5. ¿Qué propiedades\(Y\) necesita tener el dígrafo para una relación de\(X\) a fin de que represente una función?

Problema 8.6. En la preparatoria es posible que te hayan dicho que una gráfica representa una función si pasa la prueba de línea vertical. Exponga cuidadosamente lo que dice la prueba de línea vertical y luego explique por qué funciona.

A veces podemos definir una función usando una fórmula. Por ejemplo, podemos escribir\(f(x)=x^2-1\) para significar que cada uno\(x\) en el dominio de\(f\) mapas a\(x^2-1\) en el codominio. Sin embargo, ¡fíjate que proporcionar solo una fórmula es ambiguo! Una función está determinada por su dominio, codominio y la correspondencia entre estos dos conjuntos. Si solo proporcionamos una descripción para la correspondencia, no está claro cuáles son el dominio y el codominio. Dos funciones que están definidas por la misma fórmula, pero que tienen diferentes dominios o codominios no son iguales.

Ejemplo 8.7. La función\(f:\mathbb{R}\to \mathbb{R}\) definida via no\(f(x)=x^{2}-1\) es igual a la función\(g:\mathbb{N}\to\mathbb{R}\) definida por\(g(x)=x^{2}-1\) ya que las dos funciones no tienen el mismo dominio.

A veces nos basamos en el contexto para interpretar el dominio y el codominio. Por ejemplo, en una clase de cálculo, cuando describimos una función en términos de una fórmula, estamos asumiendo implícitamente que el dominio es el subconjunto más grande permitido de\(\mathbb{R}\) —a veces llamado dominio predeterminado —que tiene sentido para la fórmula dada mientras que el codominio es \(\mathbb{R}\).

Ejemplo 8.8. Si escribimos\(f(x)=x^2-1\),\(g(x)=\sqrt{x}\), y\(h(x)=\frac{1}{x}\) sin mencionar los dominios, normalmente interpretaríamos estos como las funciones\(f:\mathbb{R}\to \mathbb{R}\),\(g:[0,\infty)\to \mathbb{R}\), y\(h:\mathbb{R}\setminus \{0\}\to \mathbb{R}\) que están determinados por sus respectivas fórmulas.

Problema 8.9. Proporcione un ejemplo de cada uno de los siguientes. Puede dibujar un diagrama de funciones, escribir una lista de pares ordenados o escribir una fórmula siempre que el dominio y el codominio estén claros.

1. Una función\(f\) de un conjunto con 4 elementos a un conjunto con 3 elementos tales que\(\range(f)=codom(f)\).
2. Una función\(g\) de un conjunto con 4 elementos a un conjunto con 3 elementos tal que\(\range(g)\) es estrictamente más pequeño que\(codom(g)\).

Problema 8.10. Dejar\(f:X\to Y\) ser una función y supongamos que\(X\) y\(Y\) son conjuntos finitos con\(n\) y\(m\) elementos, respectivamente, tales que\(n<m\). ¿Es posible para\(\range(f)=codom(f)\)? Si es así, dar un ejemplo. Si esto no es posible, explique por qué.

Hay algunas funciones especiales de las que debemos conocer los nombres.

Definición 8.11. Si\(X\) y\(Y\) son conjuntos no vacíos de tal manera que\(X\subseteq Y\), entonces la función\(\iota:X\to Y\) definida via\(\iota(x)=x\) se llama el mapa de inclusión de\(X\) en\(Y\).

Tenga en cuenta que “\(\iota\)" es la letra griega “iota”.

Problema 8.12. Dejar\(X=\{a,b,c\}\) y\(Y=\{a,b,c,d\}\). Dibuja el diagrama de funciones del mapa de inclusión de\(X\) hacia\(Y\).

Si el dominio y el codominio son iguales, el mapa de inclusión tiene un nombre especial.

Definición 8.13. Si\(X\) es un conjunto no vacío, entonces la función\(i_X:X\to X\) definida vía\(i_X(x)=x\) se llama el mapa de identidad (o función de identidad) on\(X\).

Ejemplo 8.14. La relación definida en Problema 8.4 (7) es el mapa de identidad en\(X=\{\circ, \square,\triangle,smiley\}\).

Problema 8.15. Dibuja una parte de la gráfica del mapa de identidad\(\mathbb{R}\) como un subconjunto de\(\mathbb{R}^2\).

Problema 8.16. Dejar\(A\) ser un conjunto no vacío.

1. Supongamos que\(R\) es una relación de equivalencia sobre\(A\). ¿Qué condiciones\(R\) deben mantenerse\(R\) para que sea una función de\(A\) a\(A\)?
2. Supongamos que\(f:A\to A\) es una función. ¿En qué condiciones se encuentra\(f\) una relación de equivalencia\(A\)?

Definición 8.17. Cualquier función\(f:X\to Y\) definida vía\(f(x)=c\) para un fijo\(c\in Y\) se llama una función constante.

Ejemplo 8.18. La función definida en Problema 8.4 (8) es un ejemplo de una función constante. Observe que podemos describir sucintamente esta función usando la fórmula\(\operatorname{happy}(y)=smiley\).

Definición 8.19. Una función definida por partes (o función por partes) es una función definida especificando su salida en una partición del dominio.

Tenga en cuenta que “por partes” es una forma de expresar la función, más que una propiedad de la función misma.

Ejemplo 8.20. Podemos expresar la función en Problema 8.4 (9) como una función por partes usando la fórmula\[\operatorname{nugget}(x)=\begin{cases} x, & \mbox{if } x\mbox{ is a geometric shape},\\ \square, & \mbox{otherwise}. \end{cases}\]

Ejemplo 8.21. La función\(f:\mathbb{R}\to \mathbb{R}\) definida vía\[f(x)=\begin{cases} x^2-1, & \mbox{if } x\geq 0,\\ 17, & \mbox{if } -2\leq x< 0,\\ -x, & \mbox{if } x<-2 \end{cases}\] es un ejemplo de una función definida por partes.

Problema 8.22. Definir\(f:\mathbb{R}\setminus\{0\}\to \mathbb{R}\) vía\(f(x)=\frac{|x|}{x}\). Expresar\(f\) como una función por partes.

¡Es importante señalar que no todas las funciones pueden describirse usando una fórmula! A pesar de su experiencia previa, las funciones que se pueden representar de manera sucinta usando una fórmula son raras.

El siguiente problema ilustra que se debe tener cierto cuidado al intentar definir una función.

Problema 8.23. Para cada una de las siguientes, explique por qué la descripción dada no define una función.

1. Definir\(f:\{1,2,3\}\to \{1,2,3\}\) vía\(f(a)=a-1\).
2. Definir\(g:\mathbb{N}\to \mathbb{Q}\) vía\(g(n)=\frac{n}{n-1}\).
3. Dejar\(A_1=\{1,2,3\}\) y\(A_2=\{3,4,5\}\). Definir\(h:A_1\cup A_2\to \{1,2\}\) vía\[h(x)=\begin{cases} 1, & \mbox{if }x\in A_1\\ 2, & \mbox{if }x\in A_2. \end{cases}\]
4. Definir\(s:\mathbb{Q}\to \mathbb{Z}\) vía\(s(a/b)=a+b\).

En matemáticas, decimos que una expresión está bien definida (o inequívoca) si su definición produce una interpretación única. De lo contrario, decimos que la expresión no está bien definida (o es ambigua). Por ejemplo, si\(a,b,c\in\mathbb{R}\), entonces la expresión\(abc\) está bien definida ya que no importa si interpretamos esto como\((ab)c\) o\(a(bc)\) ya que los números reales son asociativos bajo multiplicación. Este número acechaba detrás de escena en la declaración del Teorema 7.94. En particular, las expresiones\[[a_1]_n+[a_2]_n+\cdots+ [a_k]_n\] y\[[a_1]_n [a_2]_n \cdots [a_k]_n\] están bien definidas a la\(\mathbb{Z}/n\mathbb{Z}\) luz de los Teoremas 7.92 (2) y 7.93 (2).

Cuando intentamos definir una función, puede que no quede claro sin hacer algún trabajo que nuestra definición realmente arroja una función. Si hay alguna ambigüedad potencial en la definición de una función que termina por no causar ningún problema, decimos que la función está bien definida. Sin embargo, esta frase es un poco inapropiada ya que todas las funciones están bien definidas. La cuestión de si una descripción para una función propuesta está bien definida a menudo surge al definir cosas en términos de representantes de clases de equivalencia, o más generalmente en términos de cómo se escribe un elemento del dominio. Por ejemplo, las descripciones dadas en las Partes (c) y (d) del Problema 8.23 no están bien definidas. Para demostrar que una descripción potencialmente ambigua para una función\(f:X\to Y\) está bien definida probar que si\(a\) y\(b\) son dos representaciones para el mismo elemento en\(X\), entonces\(f(a)=f(b)\).

Problema 8.24. Para cada una de las siguientes, determine si la descripción determina una función bien definida.

1. Definir\(f:\mathbb{Z}/5\mathbb{Z}\to \mathbb{N}\) vía\[f([a]_5)=\begin{cases} 0, & \mbox{if } a\mbox{ is even}\\ 1, & \mbox{if } a\mbox{ is odd}. \end{cases}\]
2. Definir\(g:\mathbb{Z}/6\mathbb{Z}\to \mathbb{N}\) vía\[g([a]_6)=\begin{cases} 0, & \mbox{if } a\mbox{ is even}\\ 1, & \mbox{if } a\mbox{ is odd}. \end{cases}\]
3. Definir\(m:\mathbb{Z}/8\mathbb{Z}\to \mathbb{Z}/10\mathbb{Z}\) vía\(m([x]_{8})=[6x]_{10}\).
4. Definir\(h:\mathbb{Z}/10\mathbb{Z}\to \mathbb{Z}/10\mathbb{Z}\) vía\(h([x]_{10})=[6x]_{10}\).
5. Definir\(k:\mathbb{Z}/43\mathbb{Z}\to \mathbb{Z}/43\mathbb{Z}\) vía\(k([x]_{43})=[11x-5]_{43}\).
6. Definir\(\ell:\mathbb{Z}/15\mathbb{Z}\to \mathbb{Z}/15\mathbb{Z}\) vía\(\ell([x]_{15})=[5x-11]_{15}\).

Problema 8.25. Dejar\(k,n\in\mathbb{N}\) y\(m\in\mathbb{Z}\). ¿Bajo qué condiciones\(f_m: \mathbb{Z}/n\mathbb{Z}\to \mathbb{Z}/k\mathbb{Z}\) dará por\(f_m([x]_n) = [mx]_k\) ser una función bien definida? Demuestra tu reclamo.