9.1: Introducción a la Cardenalidad

En este capítulo, exploraremos la noción de cardinalidad, que formaliza lo que significa que dos conjuntos sean del mismo “tamaño”.

¿Qué significa que dos conjuntos tengan el mismo “tamaño”? Si los conjuntos son finitos, esto es fácil: solo cuente cuántos elementos hay en cada conjunto. Otro enfoque sería emparejar los elementos en cada conjunto y ver si hay sobrantes. En otras palabras, verifique si existe una correspondencia uno a uno (es decir, biyección) entre los dos conjuntos.

Pero, ¿y si los conjuntos son infinitos? Por ejemplo, considere el conjunto de números naturales\(\mathbb{N}\) y el conjunto de números naturales pares\(2\mathbb{N}:= \{2n\mid n\in \mathbb{N}\}\). Claramente,\(2\mathbb{N}\) es un subconjunto apropiado de\(\mathbb{N}\). Además, ambos conjuntos son infinitos. En este caso, podrías estar pensando que\(\mathbb{N}\) es “más grande que”\(2\mathbb{N}\). No obstante, resulta que existe una correspondencia uno a uno entre estos dos conjuntos. En particular, considere la función\(f:\mathbb{N}\to 2\mathbb{N}\) definida vía\(f(n)=2n\). Se verifica fácilmente que\(f\) es tanto inyectivo como surytivo. En este caso, las matemáticas han determinado que el punto de vista correcto es eso\(\mathbb{N}\) y\(2\mathbb{N}\) sí tienen el mismo “tamaño”. No obstante, es claro que el “tamaño” es un poco impreciso cuando se trata de conjuntos infinitos. Necesitamos algo más riguroso.

Definición 9.1. Dejar\(A\) y\(B\) ser conjuntos. Eso decimos\(A\) y\(B\) tenemos la misma cardinalidad si existe una biyección entre\(A\) y\(B\). En este caso, escribimos\(card(A)=card(B)\).

Tenga en cuenta que no hemos definido\(card(A)\) por sí mismo. Hacerlo no sería demasiado difícil para los conjuntos finitos, pero hacer que tal notación sea precisa en general es un asunto complicado. Cuando escribimos\(card(A)=card(B)\) (y después\(card(A)\leq card(B)\) y\(card(A)<card(B)\)), estamos afirmando la existencia de cierto tipo de función de\(A\) a\(B\).

Si\(f\) es una biyección de\(A\) a\(B\), entonces por el Teorema 8.77,\(f^{-1}\) es una biyección de\(B\) a\(A\). Cualquiera de estas funciones puede ser utilizada para demostrarlo\(card(A)=card(B)\). Vale la pena tenerla en cuenta a medida que abordes problemas en este capítulo. En particular, es posible que te resulte más fácil crear una bijección entre dos conjuntos en una dirección sobre la otra. Esto suele ser una limitación de la mente humana en oposición a alguna dificultad matemática fundamental.

Ejemplo 9.2. Dejar\(A=\{1,2,3,4,5\}\) y\(B=\{\text{apple},\text{banana},\text{cherry},\text{dragon fruit},\text{elderberry}\}\). La función\(f:A\to B\) dada por\[f=\{(1,\text{apple}),(2,\text{banana}),(3,\text{cherry}),(4,\text{dragon fruit}),(5,\text{elderberry})\}\] es una bijección de\(A\) a\(B\), y por lo tanto\(card(A)=card(B)\). Tenga en cuenta que esta no es la única bijección de\(A\) a\(B\). De hecho, hay\(5!=120\) bijecciones de\(A\) a\(B\), una de las cuales es la función que\(f\) definimos anteriormente. La inversa de cada bijección de\(A\) a\(B\) es una bijección de\(B\) a\(A\). También podríamos usar cualquiera de estas bijecciones para verificar eso\(card(A)=card(B)\).

Ejemplo 9.3. Definir\(f:\mathbb{Z}\to 6\mathbb{Z}\) vía\(f(n)=6n\). Se verifica fácilmente que\(f\) es tanto inyectivo como surytivo, y por lo tanto\(card(\mathbb{Z})=card(6\mathbb{Z})\). También podríamos utilizar la función inversa\(f^{-1}:6\mathbb{Z}\to \mathbb{Z}\) dada por\(f^{-1}(n)=\frac{1}{6}n\) para mostrar eso\(\mathbb{Z}\) y\(6\mathbb{Z}\) tener la misma cardinalidad.

Ejemplo 9.4. Vamos a\(\mathbb{R}^+\) denotar el conjunto de números reales positivos y definir\(f:\mathbb{R}\to \mathbb{R}^+\) vía\(f(x)=e^x\). Como probablemente estés familiarizado con, esta función exponencial es una biyección, y así\(card(\mathbb{R})=card(\mathbb{R}^+)\). Similar al ejemplo anterior, también podríamos usar la función inversa\(f^{-1}:\mathbb{R}^+\to \mathbb{R}\) dada por\(f^{-1}(x)=\ln(x)\) para mostrar que estos dos conjuntos tienen la misma cardinalidad.

Los dos ejemplos anteriores ilustran una distinción importante entre conjuntos finitos y conjuntos infinitos, es decir, ¡los conjuntos infinitos pueden estar en bijección con subconjuntos adecuados de sí mismos! Los teoremas 9.23 y 9.31 harán explícita esta idea.

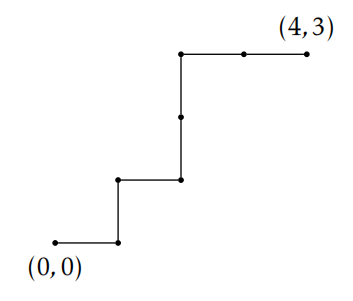
Ejemplo 9.5. Vamos\(m,n\in\mathbb{N}\cup\{0\}\). Un camino de celosía noreste de\((0,0)\) a\((m,n)\) es camino en el plano de\((0,0)\) a\((m,n)\) que consiste solo escalona una unidad Norte o una unidad Este. Tenga en cuenta que cada camino de celosía de\((0,0)\) a\((m,n)\) consiste en un total de\(m+n\) pasos. La Figura 9.1 muestra una trayectoria de celosía noreste de\((0,0)\) a\((4,3)\). Vamos\(\mathcal{L}_{m,n}\) denotar el conjunto de caminos del noreste de\((0,0)\) a\((m,n)\). Por ejemplo, la trayectoria de celosía noreste dada en la Figura 9.1 es un elemento de\(\mathcal{L}_{4,3}\). Una cadena binaria de longitud\(k\) es una lista ordenada que consta de\(k\) entradas donde cada entrada es 0 o 1. Por ejemplo,\(0101100\) y\(0101001\) son dos cadenas binarias diferentes de longitud 7. Dejar\(\mathcal{S}_k\) denotar el conjunto de cadenas binarias de longitud\(k\). Por ejemplo,\(\mathcal{S}_3=\{000, 100,010,001,110,101,011,111\}\). Afirmamos que hay una bijección entre\(\mathcal{L}_{m,n}\) y\(\mathcal{S}_{m+n}\). Una de esas bijección se da mapeando una ruta de celosía a la cadena que resulta asignando cada paso Este a 0 y cada paso Norte a 1 a medida que recorremos el camino de\((0,0)\) a\((m,n)\). Usando esta construcción, la ruta de celosía en la Figura 9.1 se mapearía a la cadena binaria\(0101100\). Dado que no hay dos rutas de celosía mapeadas a la misma cadena, nuestro mapeo es inyectivo. Dada una cadena en\(\mathcal{S}_{m+n}\), es fácil encontrar la ruta de celosía en\(\mathcal{L}_{m,n}\) ese mapa, y así nuestra función también es surjectiva. Así, nuestro mapeo es una biyección entre\(\mathcal{L}_{m,n}\) y\(\mathcal{S}_{m+n}\). Eso lo hemos demostrado\(card(\mathcal{L}_{m,n})=card(\mathcal{S}_{m+n})\).

= [círculo, dibujar, relleno = negro, sep=0pt interior, tamaño mínimo=.7mm]

Al acercarse a la Parte (d) del siguiente problema, intente crear una función lineal\(f:(a,b)\to (c,d)\). Dibujar un cuadro debería ayudar.

Problema 9.6. Demostrar cada uno de los siguientes. En cada caso, debes crear una bijección entre los dos conjuntos. Justifica brevemente que tus funciones son en realidad bijecciones.

Figura 9.1: Una trayectoria de celosía noreste de (0,0) a (4,3).

1. \(card(\{a,b,c\})=card(\{x,y,z\})\)
2. \(card(\mathbb{N})=card(\{2n+1\mid n\in \mathbb{N}\})\)
3. \(card(\mathbb{N})=card(\mathbb{Z})\)
4. \(card((a,b))=card((c,d))\)(donde\((a,b)\) y\((c,d)\) son intervalos)
5. \(card(\mathbb{N})=card(\{\frac{1}{2^n}\mid n\in \mathbb{N}\})\)

Problema 9.7. Si\(A\) es un conjunto, ¿\(A\)y\(A\times \{x\}\) tienen la misma cardinalidad? Justifica tu respuesta.

Problema 9.8. Dejar\(\mathcal{D}_n\) denotar la colección de caminos de celosía del noreste desde\((0,0)\) hasta\((n,n)\) que nunca caen por debajo de la línea\(y=x\). Este tipo de caminos de celosía a menudo se llaman caminos Dyck después del matemático alemán Walther Franz Anton von Dyck (1856—1934). Una secuencia de paréntesis se equilibra si se puede analizar sintácticamente. Es decir, debe haber el mismo número de paréntesis abiertos “(” y paréntesis cerrados “)”, y al leer de izquierda a derecha nunca debe haber más paréntesis cerrados que abiertos. Por ejemplo,\(()()()\) y\(()(())\) son paréntesis equilibrados que constan de tres pares de paréntesis mientras que\(())(()\) y no\(()(()(\) están equilibrados. Dejar\(\mathcal{B}_n\) denotar la colección de paréntesis balanceados que consiste en\(n\) pares de paréntesis. Por ejemplo,\(\mathcal{B}_3=\{()()(), ()(()), (()()), (())(), ((()))\}\).

1. Encuentra todos los caminos de Dyck en\(\mathcal{D}_3\).
2. \(card(\mathcal{D}_n)=card(\mathcal{B}_n)\)Demuéstralo.

Para la Parte (b) del siguiente problema, comience definiendo de\(\varphi:\mathcal{F}\to \mathcal{P}(\mathbb{N})\) manera que\(\varphi(f)\) arroje un subconjunto de\(\mathbb{N}\) determinado por cuando\(f\) emita un 1.

Problema 9.9. Dejar\(\mathcal{F}\) denotar el conjunto de funciones de\(\mathbb{N}\) a\(\{0,1\}\).

1. Describir al menos tres funciones en\(\mathcal{F}\).
2. Demostrarlo\(\mathcal{F}\) y\(\mathcal{P}(\mathbb{N})\) tener la misma cardinalidad.

Nuestro primer teorema relativo a la cardinalidad probablemente no será una sorpresa.

Teorema 9.10. Dejar\(A\),\(B\), y\(C\) ser conjuntos.

1. \(card(A)=card(A)\).
2. Si\(card(A)=card(B)\), entonces\(card(B)=card(A)\).
3. Si\(card(A)=card(B)\) y\(card(B)=card(C)\), entonces\(card(A)=card(C)\).

A la luz del teorema anterior, el siguiente resultado no debería sorprender.

Corolario 9.11. Si\(X\) es un conjunto, entonces “tiene la misma cardinalidad que” es una relación de equivalencia sobre\(\mathcal{P}(X)\).

Teorema 9.12. Dejar\(A\),\(B\),\(C\), y\(D\) ser conjuntos tal que\(card(A)=card(C)\) y\(card(B)=card(D)\).

1. Si\(A\) y\(B\) son disjuntas y\(C\) y\(D\) son disjuntas, entonces\(card(A\cup B)=card(C\cup D)\).
2. \(card(A\times B)=card(C\times D)\).

Dados dos conjuntos finitos, tiene sentido decir que un conjunto es “más grande que” otro siempre que un conjunto contenga más elementos que el otro. Nos gustaría generalizar esta idea para manejar conjuntos finitos e infinitos.

Definición 9.13. Dejar\(A\) y\(B\) ser conjuntos. Si hay una función inyectora de\(A\) a\(B\), entonces decimos que la cardinalidad de\(A\) es menor o igual a la cardinalidad de\(B\). En este caso, escribimos\(card(A)\leq card(B)\).

Teorema 9.14. Dejar\(A\),\(B\), y\(C\) ser conjuntos.

1. Si\(A\subseteq B\), entonces\(card(A)\leq card(B)\).
2. Si\(card(A)\leq card(B)\) y\(card(B)\leq card(C)\), entonces\(card(A)\leq card(C)\).
3. Si\(C\subseteq A\) mientras\(card(B)=card(C)\), entonces\(card(B)\leq card(A)\).

Podría ser tentador pensar que la existencia de una función inyectora de un conjunto\(A\) a un conjunto\(B\) que no es suryectiva verificaría eso\(card(A)\leq card(B)\) y\(card(A)\neq card(B)\). Si bien esto es cierto para conjuntos finitos, no es cierto para conjuntos infinitos ya que el siguiente problema te pide verificar.

Problema 9.15. Dar un ejemplo de conjuntos\(A\) y\(B\) tal que\(card(A)=card(B)\) a pesar de que existe una función inyectora desde\(A\) hasta\(B\) que no sea suryectiva.

Definición 9.16. Dejar\(A\) y\(B\) ser conjuntos. Escribimos\(card(A)< card(B)\) si\(card(A)\leq card(B)\) y\(card(A)\neq card(B)\).

Como recordatorio, las declaraciones\(card(A)= card(B)\) y\(card(A)\leq card(B)\) son formas simbólicas de afirmar la existencia de ciertos tipos de funciones desde\(A\) hasta\(B\). Cuando escribimos\(card(A)<card(B)\), estamos diciendo algo mucho más fuerte que “Existe una función\(f:A\to B\) que es inyectiva pero no suryectiva”. El enunciado\(card(A)<card(B)\) está aseverando que toda función inyectora de\(A\) a no\(B\) es suryectiva. En general, es difícil probar declaraciones como\(card(A)\neq card(B)\) o\(card(A)<card(B)\).