9.4: Conjuntos Contables

Recordemos que si\(A=\emptyset\), entonces decimos que\(A\) tiene cardinalidad 0. También, si es\(card(A)=card([n])\) por\(n\in\mathbb{N}\), entonces decimos que\(A\) tiene cardinalidad\(n\). Tenemos una forma especial de describir conjuntos que están en bijección con los números naturales.

Definición 9.36. Si\(A\) es un conjunto tal que\(card(A)=card(\mathbb{N})\), entonces decimos que\(A\) es denumerable y tiene cardinalidad\(\mathbf{\aleph_0}\) (léase “aleph nada”).

Observe si un conjunto\(A\) tiene cardinalidad\(1,2,\ldots\)\(\aleph_0\), o bien, podemos etiquetar los elementos\(A\) como “primero”, “segundo”, y así sucesivamente. Es decir, podemos “contar” los elementos en estas situaciones. Ciertamente, si un conjunto tiene cardinalidad 0, contar no es un problema. Esta idea lleva a la siguiente definición.

Definición 9.37. Un conjunto\(A\) se llama contable si\(A\) es finito o denumerable. Un conjunto se llama incontable si no es contable.

Problema 9.38. Justifica rápidamente que cada uno de los siguientes conjuntos es contable. Siéntase libre de apelar a problemas anteriores. ¿Qué conjuntos son denumerables?

1. \(\{a,b,c\}\)
2. Conjunto de números naturales impares
3. Conjunto de números naturales pares
4. \(\{\frac{1}{2^n}\mid n\in \mathbb{N}\}\)
5. Conjunto de cuadrados perfectos en\(\mathbb{N}\)
6. \(\mathbb{Z}\)
7. \(\mathbb{N}\times \{a\}\)

Utilizar el Teorema 9.31 o Corolario 9.33 al probar el siguiente resultado.

Teorema 9.39. Cada conjunto infinito contiene un subconjunto denumerable.

Teorema 9.40. Dejar\(A\) y\(B\) ser conjuntos tal que\(A\) sea contable. Si\(f:A\to B\) es una biyección, entonces\(B\) es contable.

Para la siguiente prueba, considere los casos cuando\(A\) es finito versus infinito. El contrapositivo de Corolario 9.32 debería ser útil para el caso cuando\(A\) es finito.

Teorema 9.41. Cada subconjunto de un conjunto contable es contable.

Teorema 9.42. Un conjunto es contable si y sólo si tiene la misma cardinalidad de algún subconjunto de los números naturales.

Teorema 9.43. Si\(f:\mathbb{N}\to A\) es una función suryectiva, entonces\(A\) es contable.

Hablando vagamente, el siguiente teorema nos dice que podemos organizar todos los números racionales luego contarlos “primero”, “segundo”, “tercero”, etc. Dado el hecho de que entre dos números racionales distintos cualesquiera en la recta numérica, hay un número infinito de otros números racionales (justificados tomando repetidos puntos medios), esto puede parecer contrario a la intuición.

Aquí hay un enfoque posible para probar el siguiente teorema. Hacer una mesa con encabezados de columna\(0, 1, -1, 2,-2,\ldots\) y encabezados de fila\(1,2,3,4,5,\ldots\). Si una columna tiene encabezado\(m\) y una fila tiene encabezado\(n\), entonces la entrada en la tabla corresponde a la fracción\(m/n\). Encuentra una manera de zig-zag a través de la mesa asegurándote de golpear cada entrada de la mesa (sin incluir los encabezados de columna y fila) exactamente una vez. Esto justifica que haya una bijección entre\(\mathbb{N}\) y las entradas en la tabla. ¿Ves por qué? Pero ahora noten que cada número racional aparece un número infinito de veces en la tabla. Resuelve esto apelando al Teorema 9.41.

Teorema 9.44. El conjunto de números racionales\(\mathbb{Q}\) es contable.

Teorema 9.45. Si\(A\) y\(B\) son conjuntos contables, entonces\(A\cup B\) es contable.

Nos gustaría probar un resultado más fuerte que el teorema anterior. Para ello, necesitamos un resultado intermedio.

Teorema 9.46. Dejar\(\{A_n\}_{n=1}^{\infty}\) ser una colección de conjuntos. Definir\(B_1:= A_1\) y para cada número natural\(n>1\), definir\[B_n:= A_n\setminus \bigcup_{i=1}^{n-1}A_i.\] Luego tenemos lo siguiente:

1. La colección\(\{B_n\}_{n=1}^{\infty}\) es disjunta por pares.
2. \(\displaystyle \bigcup_{n=1}^{\infty}A_n =\bigcup_{n=1}^{\infty}B_n\).

El siguiente teorema establece que la unión de una colección contable de conjuntos contables es contable. Para probarlo, considere dos casos:

1. La colección de conjuntos es finita.
2. La colección de conjuntos es infinita.

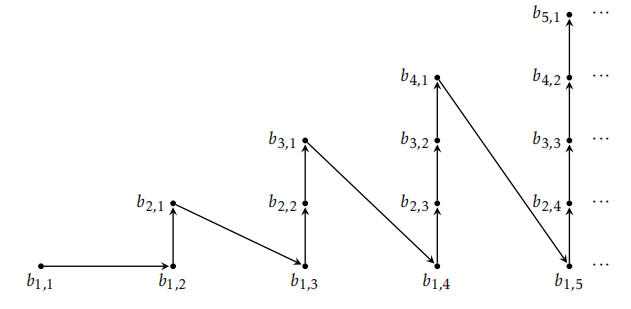
Para manejar el primer caso, utilice la inducción junto con el Teorema 9.45. El segundo caso es sustancialmente más desafiante. Primero, use el Teorema 9.46 para construir una colección\(\{B_n\}\) de conjuntos disjuntos por pares cuya unión sea igual a la unión de la colección original. Dado que cada uno\(B_n\) es un subconjunto de uno de los conjuntos de la colección original y cada uno de estos conjuntos es contable, cada uno también\(B_n\) es contable por el Teorema 9.41. Esto implica que para cada uno\(n\), podemos escribir\(B_n=\{b_{n,1}, b_{n,2},b_{n,3},\ldots\}\), donde el conjunto puede ser finito o infinito. A partir de aquí, esbozamos dos enfoques diferentes para continuar. Un enfoque es construir una bijección desde\(\mathbb{N}\) hasta\(\bigcup_{n=1}^{\infty}B_n\) usando la Figura 9.2 como inspiración. Una cosa que tendrás que abordar es qué hacer cuando un conjunto de la colección\(\{B_n\}\) es finito. Para el segundo abordaje, definir\(f:\bigcup_{n=1}^{\infty}B_n\to \mathbb{N}\) vía\(f(b_{n,m})=2^n3^m\), verificar que esta función es inyectiva, y luego apelar al Teorema 9.41. Intente usar ambos enfoques al abordar la prueba del siguiente teorema.

= [círculo, dibujar, relleno = negro, sep=0pt interior, tamaño mínimo=.7mm]

Teorema 9.47. Dejar\(\Delta\) ser igual a cualquiera\(\mathbb{N}\) o\([k]\) para algunos\(k\in\mathbb{N}\). Si\(\{A_n\}_{n\in\Delta}\) es una colección contable de conjuntos tal que cada uno\(A_n\) es contable, entonces\(\bigcup_{n\in \Delta}A_n\) es contable.

¿Utiliza el Axioma de Elección al probar el teorema anterior? Si es así, ¿dónde?

Teorema 9.48. Si\(A\) y\(B\) son conjuntos contables, entonces\(A\times B\) es contable.

Teorema 9.49. El conjunto de todas las secuencias finitas de 0 y 1 (por ejemplo,\(0110010\) es una secuencia finita que consiste en 0 y 1') es contable.

Figura 9.2: Inspiración para una posible aproximación a la prueba del Teorema 9.47.

Teorema 9.50. La colección de todos los subconjuntos finitos de un conjunto contable es contable.