2.1: TMS XVI #1
( \newcommand{\kernel}{\mathrm{null}\,}\)
1 El 4to del ancho, desde el largo y el ancho he arrancado,45′. Usted,45′
2 a 4 subir, 3 ya ves. 3, ¿qué es eso? 4 y 1 posición,
350′ y5′, para arrancar, postular. 5′a 4 elevaciones, 1 ancho. 20′a 4 elevar,
41∘20′ ya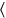 ves
ves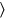 , 2 4 anchuras. 30′a 4 subir, 2 ya
, 2 4 anchuras. 30′a 4 subir, 2 ya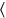 ves
ves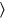 , 4 longitudes. 20′, 1 ancho, para arrancar,
, 4 longitudes. 20′, 1 ancho, para arrancar,
5 de1∘20′, 4 anchuras, arranca, 1 ya ves. 2, las longitudes, y 1, 3 anchuras, montón, 3 ya ves.
6 igi 4 desprenderse,15′ ya ves. 15′a 2, longitudes, subir,30′ ya ves
ves ,30′ la longitud.
,30′ la longitud.
715′ a 1 aumento,15′ la contribución del ancho. 30′y15′ sostenga.
8 Desde “El 4to de la anchura, para arrancar”, se te dice, de 4, 1 arranca, 3 ya ves.
9 igi 4 de tach
tach , ya15′ ves,15′ a 3 subir
, ya15′ ves,15′ a 3 subir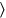 ,45′ ya45′
,45′ ya45′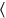 ves, tanto como (hay) de anchos.
ves, tanto como (hay) de anchos.
10 1 tanto como (hay) de longitudes postulan. 20, el ancho verdadero toma, 20 para1′ subir,20′ ya ves.
1120′ para45′ levantar,15′ ya ves. 15′de3015′ arrancar,
1230′ ya ves,30′ la longitud.
Este texto difiere en carácter de la inmensa mayoría de los textos matemáticos babilónicos antiguos: no plantea un problema, y no resuelve ninguno. En cambio, da una explicación didáctica de los conceptos y procedimientos que sirven para comprender y reducir cierto tipo de ecuación que suele ocurrir.
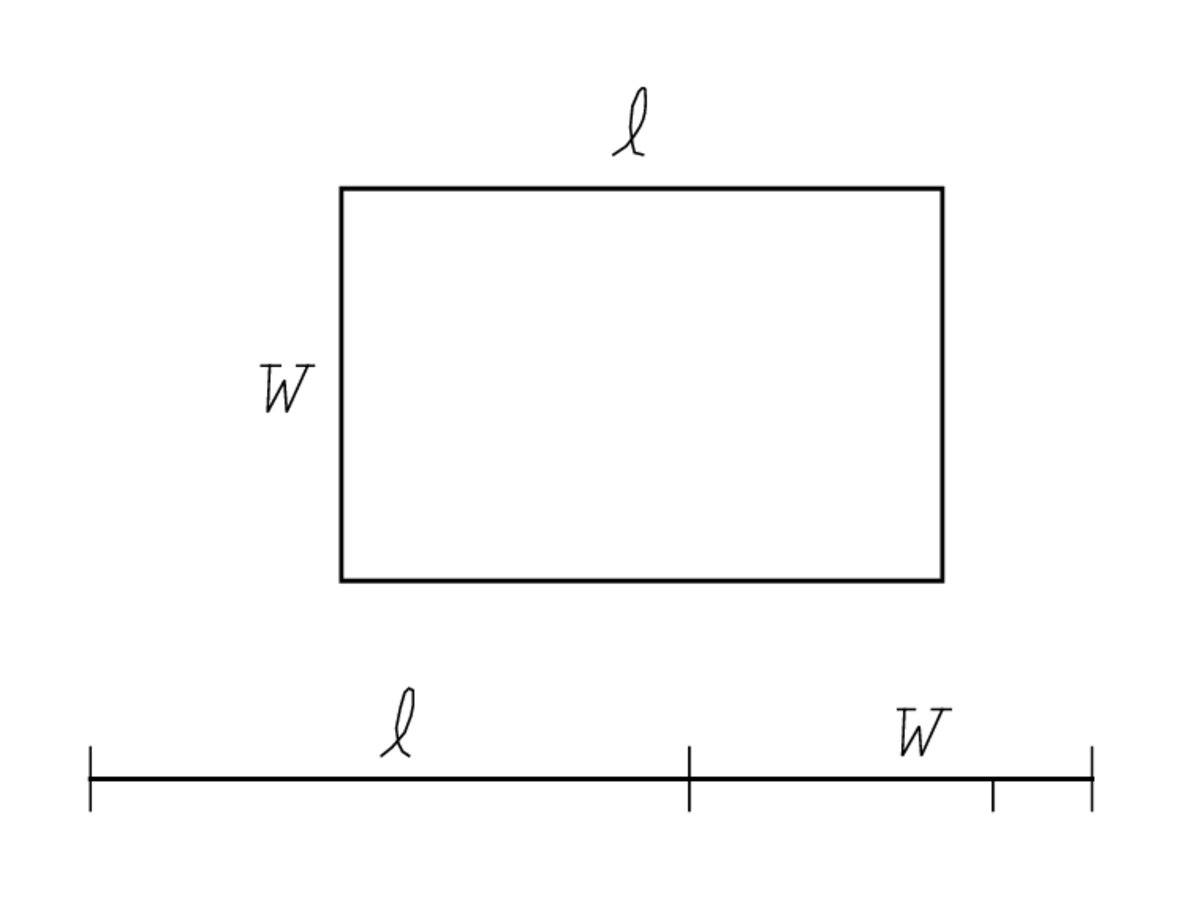
Figura2.1: La geometría del TMS XVI #1.
A pesar de que muchos de los términos que aparecen en la traducción ya fueron explicados en la sección “Una nueva interpretación”, puede ser útil pasar por el texto palabra por palabra.
La línea 1 formula una ecuación: El 4to del ancho, desde el largo y el ancho que he arrancado,45′.
Por lo tanto, la ecuación se refiere a una longitud y una anchura. Eso nos dice que el objeto es un rectángulo, desde el punto de vista babilónico antiguo, el rectángulo es la figura más simple determinada solo por una longitud y una anchura. 3 En cuanto a la notación numérica, véase el recuadro “El sistema sexagesimal”, página 14. Siℓ es la longitud yw el ancho, podemos expresar la ecuación en símbolos de esta manera:
(ℓ+w)−14w=45′.
Algo, sin embargo, se pierde en esta traducción. De hecho, la longitud y el ancho es una expresión condensada para un “amontonamiento”, la adición simétrica de dos magnitudes (o sus números de medición; ver página 18). Así, la longitud no se prolonga por la anchura, las dos magnitudes se combinan en pie de igualdad, independientemente del rectángulo. El único papel del rectángulo es poner sus dimensiones a disposición como magnitudes desconocidas (Figura 2.1).
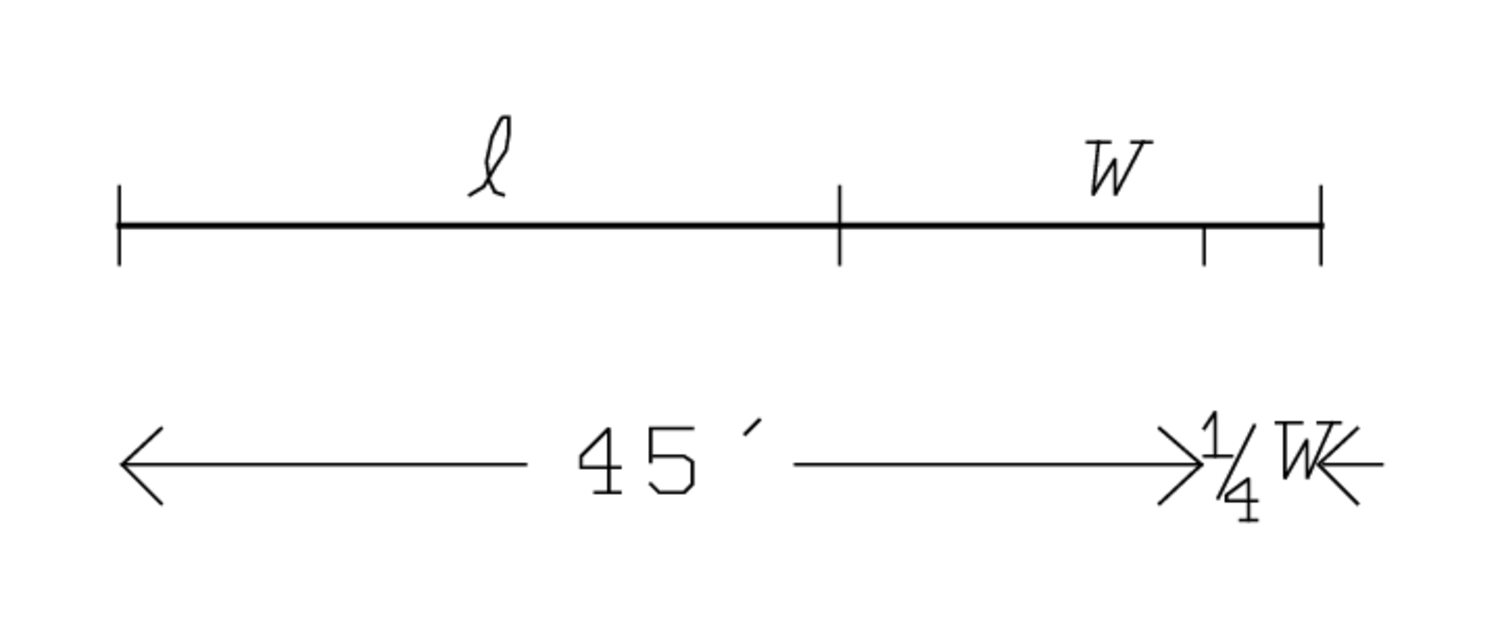
Figura2.2: “La ecuación” de TMS XVI #1.
Una vez que el largo y el ancho han sido “amontonados”, es posible “arrancar”14w, ya que esta entidad es parte del ancho y por lo tanto también del total. “arrancar” como recordamos, es la operación inversa de “unir”, y así la eliminación de una magnitud de otra de la que forma parte (Figura 2.2).
La línea 1 muestra la naturaleza de una ecuación babilónica: una combinación de magnitudes medibles (a menudo, como aquí, magnitudes geométricas), para las cuales se da el total. Alternativamente el texto establece que la medida de una combinación es igual a la de otra, o por cuanto una excede a la otra. Ese no es exactamente el tipo de ecuación que se enseña en las matemáticas escolares actuales, que normalmente se ocupa del número puro, sino que es bastante similar a las ecuaciones manipuladas por ingenieros, físicos o economistas. Hablar de “ecuaciones” en el contexto babilónico no es, pues, en absoluto anacrónico.
A continuación, las líneas 1 y 2 piden al alumno que multiplique el45′ (en el lado derecho de la versión en símbolos) por 4: Tú,45′ a 4 subir, 3 ves. Para “elevar”, recordamos de la página 13, significa multiplicar una magnitud concreta, aquí el número que representa un segmento de línea compuesto. El resultado de esta multiplicación es 3, y el texto plantea preguntas retóricas: 3, ¿qué es eso?
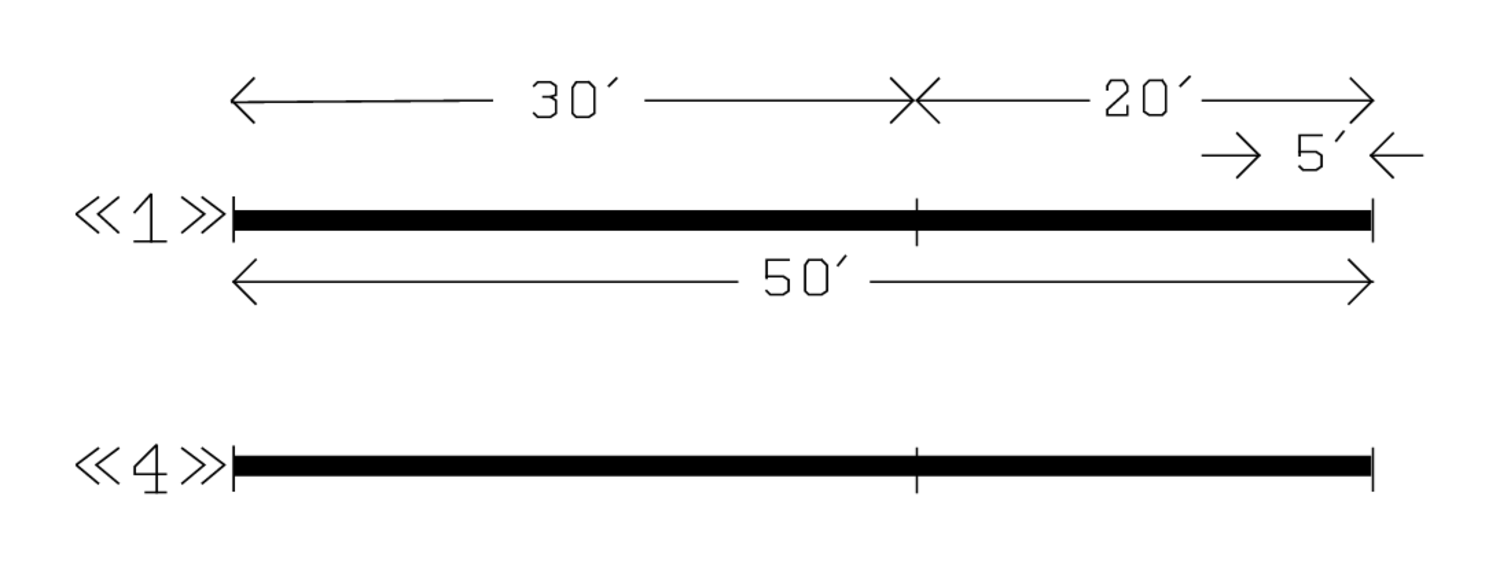
Figura2.3: Interpretación del TMS XVI, líneas 1—3.
La respuesta a esta pregunta se encuentra en las líneas 2—5. 4 y 1 postulado: Primero, el alumno debe “postular” 4 y 1. “Postular” significa dar una representación material; aquí, los números probablemente deben escribirse en el lugar apropiado en un diagrama (la Figura 2.3 es una posible interpretación). El número “1” corresponde al hecho de que el número45′ a la derecha en la ecuación inicial así como las magnitudes a la izquierda se utilizan todas una sola vez. El número “4” se “postula” porque estamos para explicar qué sucede cuando45′ y las magnitudes correspondientes se toman 4 veces.
50′y5′, para arrancar, postular: los números50′ y5′ se colocan en el nivel “1” del diagrama. Esto debería sorprendernos: demuestra que se supone que el alumno debe saber ya que el ancho es20′ y el largo es30′. Si no lo hacía, no entendería esoℓ+w=50′ y aquello14w (lo que se va a arrancar) lo es5′. En aras de la claridad no sólo los números50′ y5′ sino también30′ y20′ se indican en el nivel “1” en nuestro diagrama aunque el texto no hable de ellos.
Las líneas 3—5 demuestran aún más convincentemente que se supone que el estudiante ya conoce la solución al problema (que por lo tanto es solo un cuasi-problema). El objetivo del texto es, pues, no encontrar una solución. Como ya se dijo, es para explicar los conceptos y procedimientos que sirven para entender y reducir la ecuación.
Estas líneas explican cómo y por qué la ecuación inicial
(ℓ+w)−14w=45′
se transforma en
4ℓ+(4−1)w=3
a través de la multiplicación por 4.
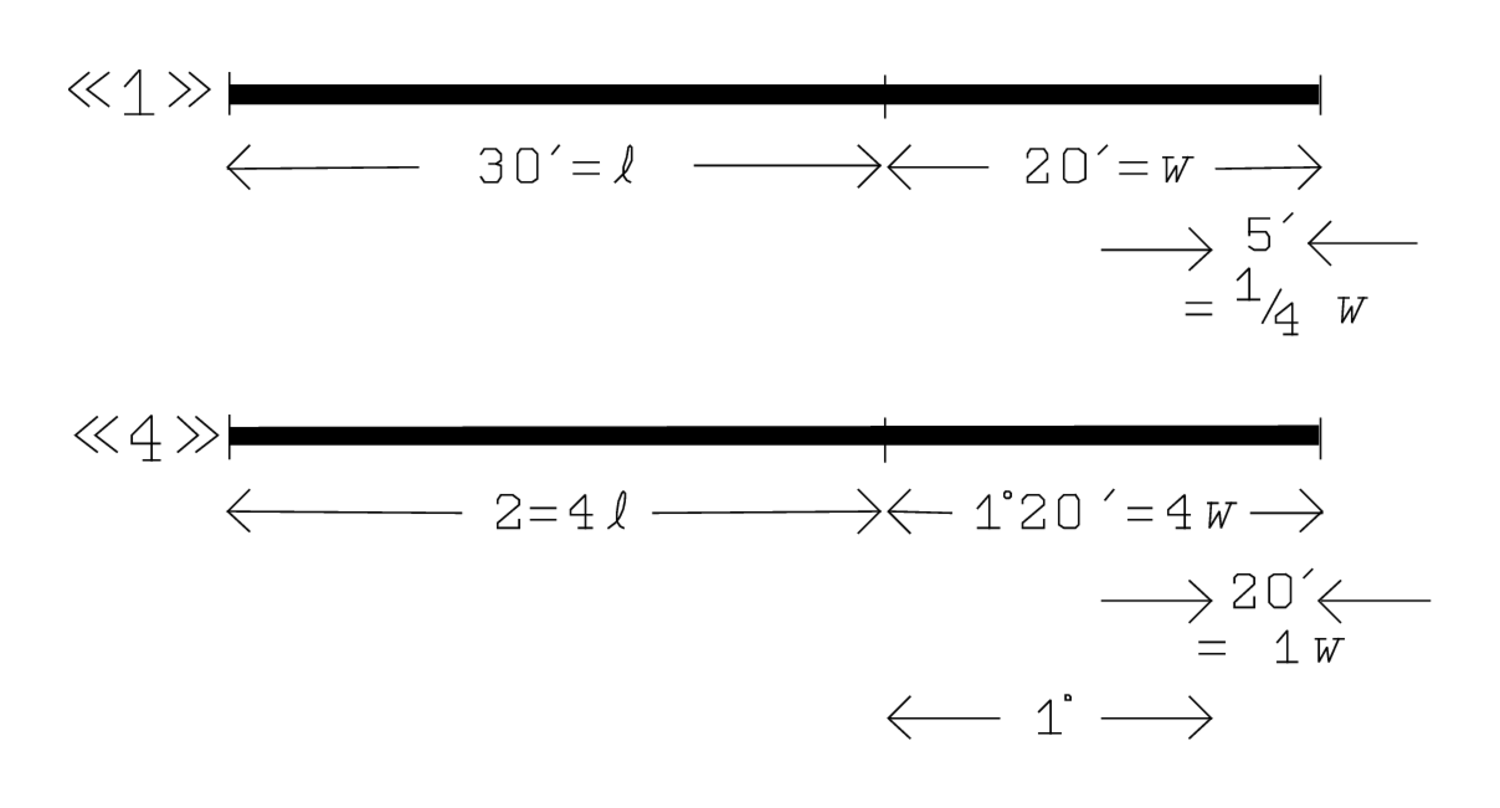
Figura2.4: Interpretación del TMS XVI, líneas 3—5.
Este cálculo se puede seguir en la Figura 2.4, donde los números en el nivel “1” se multiplican por 4, dando lugar con ello a los del nivel “4”:
5′a 4 subir, 1 ancho:5′, es decir, el14 del ancho, se multiplica por 4, de lo que resulta20′, es decir, un ancho.
20′a 4 subir,1∘20′ ya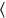 ves
ves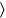 , 4 anchuras:20′, es decir, 1 ancho, se multiplica por 4, de la que proviene1∘20′, así 4 anchuras.
, 4 anchuras:20′, es decir, 1 ancho, se multiplica por 4, de la que proviene1∘20′, así 4 anchuras.
\(30′\) a 4 subir, 2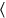 ves
ves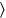 , 4 longitudes:\(30′\), es decir 1 longitud, se multiplica por 4. Esto da 2, 4 longitudes.
, 4 longitudes:\(30′\), es decir 1 longitud, se multiplica por 4. Esto da 2, 4 longitudes.
Después de haber multiplicado todos los números de nivel “1” por 4, y encontrar así sus contrapartes en el nivel “4”, el texto indica (líneas 4 y 5) lo que queda cuando se elimina 1 ancho de 4 anchuras:\(20′\), 1 ancho, para arrancar1∘20′, de, 4 anchuras, arrancar, 1 ya ves.
Finalmente,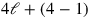
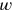 se identifican los constituyentes individuales de la suma, como se muestra en la Figura 2.5 2, se agregan las longitudes, y 1, 3 anchuras, montón, 3 ves: 2, es decir, 4 longitudes, y 1, es decir,
se identifican los constituyentes individuales de la suma, como se muestra en la Figura 2.5 2, se agregan las longitudes, y 1, 3 anchuras, montón, 3 ves: 2, es decir, 4 longitudes, y 1, es decir,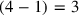 anchuras. Esto da el número 3. Ya hemos encontrado la respuesta a la pregunta de la línea 2, 3 ya ves. 3, ¿qué es eso?.
anchuras. Esto da el número 3. Ya hemos encontrado la respuesta a la pregunta de la línea 2, 3 ya ves. 3, ¿qué es eso?.
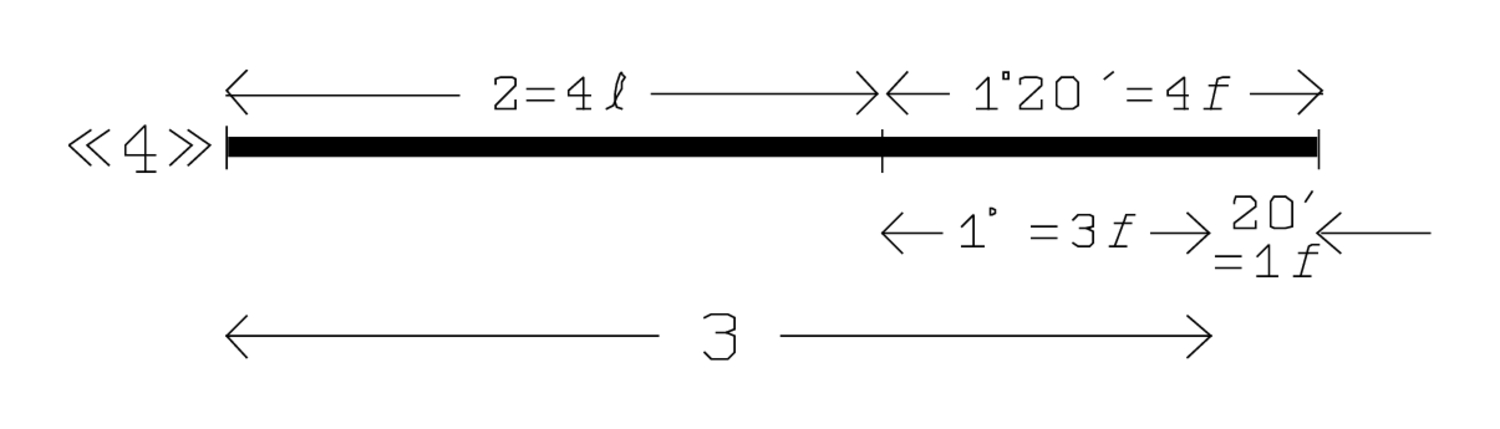
Figura2.5: Interpretación del TMS XVI, línea 5.
Pero la lección no se detiene aquí. Mientras que las líneas 1—5 explican cómo se(ℓ+w)−14w=45′ puede transformar la ecuación en4⋅ℓ+(4−1)⋅w=3, lo que sigue en las líneas 6-10 conduce, a través de la división por 4, a una transformación de esta ecuación en
1⋅ℓ+34⋅w=45′.
Para los babilonios, la división por 4 es efectivamente efectuada como una multiplicación por14. Por lo tanto, la línea 6 establece que14=15′: igi 4 desprender,15′ ya ve. igi 4 se puede encontrar en la tabla de igi, es decir, de reciprocales (ver página 20).
La Figura 2.6 muestra que esto corresponde a un retorno al nivel “1”:
15′a 2, longitudes, subir,30′ ya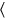 ves
ves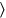 ,30′ la longitud: 2, es decir, 4 longitudes, cuando se multiplica por14 da30′, es decir, 1 longitud.
,30′ la longitud: 2, es decir, 4 longitudes, cuando se multiplica por14 da30′, es decir, 1 longitud.
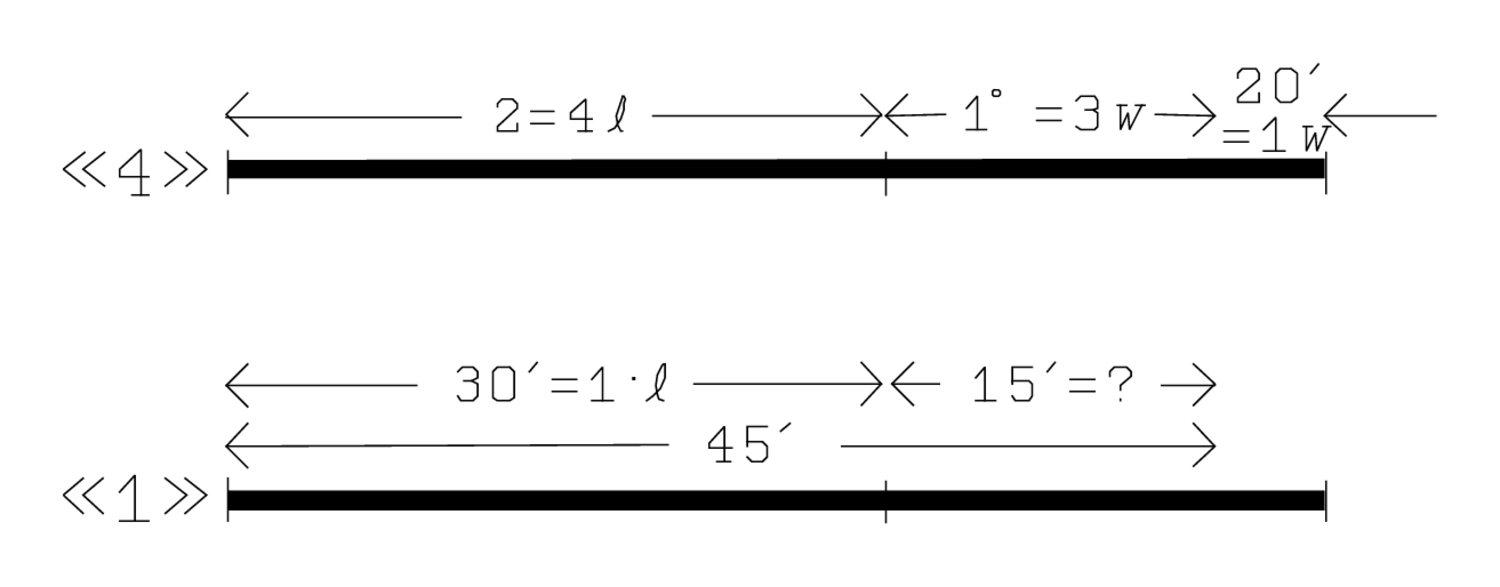
Figura2.6: Interpretación del TMS XVI, líneas 6—12.
15′a 1 aumento,15′ la contribución del ancho. (línea 7): 1, es decir, 3 anchuras, se multiplica por14, lo que da15′, la contribución del ancho a la suma45′. La cantidad de idths a que corresponde esta contribución se determina en las líneas 8 y 9. Mientras tanto, se memorizan las contribuciones de la longitud y el ancho:30′ y15′ hold —una expresión más corta para may you head hold, la formulación utilizada en otros textos. Notamos el contraste con el material tomando nota de los números 1, 4,50′ y5′ por “postulación” al principio.
El aporte de la anchura es así15′. El final de la línea 9 indica que el número de anchuras a las que eso corresponde —el coeficiente del ancho, en nuestro idioma— es34 (=45′): tanto45′ como (hay) de anchuras. el argumento que conduce a esto es de un tipo conocido como “posición falsa simple”. 4
La línea 8 cita la declaración del cuasi-problema como justificación de lo que se hace (tales justificaciones por cotización son estándar): Desde “El 4to de la anchura, para arrancar”, se le dice a usted. Por lo tanto, debemos averiguar cuánto queda del ancho cuando se14 ha eliminado.
Por conveniencia, se “postula” que la cantidad de anchos es 4 (esta es la “posición falsa”). 14de 4 es igual a 1 (el texto da este número sin cálculo). Cuando se elimina, quedan 3: de 4, 1 arranca, 3 ya ves.
Para ver a qué parte del falsamente postulado 4 este 3 corresponde, multiplicamos por14. A pesar de que esto ya se dijo en la línea 6, se repite en la línea 9 que14 corresponde a15′: igi 4 de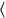 tach
tach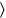 ,15′ ya ves.
,15′ ya ves.
Aún en la línea 9, la multiplicación por 3 da el coeficiente del ancho como45′ (=34):15′ a 3 subir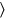 ,45′ ya45′
,45′ ya45′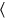 ves, tanto como (hay) de anchos.
ves, tanto como (hay) de anchos.
Sin calcularlo la línea 10 anuncia que el coeficiente de la longitud es 1. Sabemos efectivamente por la línea 1 que una única longitud entra en el45′, sin suma ni resta. Hemos explicado así cómo la ecuación4⋅ℓ+(4−1)⋅w=3 se transforma en
1⋅ℓ+34⋅w=45′.
El final de la línea 10 nos presenta un pequeño enigma: ¿cuál es la relación entre el “ancho verdadero” y el ancho que figura en las ecuaciones?
La explicación podría ser la siguiente: un campo verdadero podría medir 30 [NINDAN] por 20 [NINDAN] (c. 180 m por 120 m, es decir,13 bùr), pero ciertamente no30′ por20′ (3 m por 2 m). Por otro lado sería imposible dibujar un campo con las dimensiones30×20 en el patio de la casa del maestro (o cualquier otra escuela; en realidad, un patio sembrado de arena es el soporte más plausible para los diagramas utilizados en la enseñanza). Pero30′ por20′ encajaría perfectamente (sabemos por casas excavadas), y este orden de magnitud es el que normalmente aparece en problemas matemáticos. Dado que no hay diferencia en la escritura entre 20 y20′, esto no es más que una posible explicación —sino una plausible, ya que no parece haber alternativa disponible.
En cualquier caso, en la línea 11 se vuelve a encontrar que el ancho contribuye con15′, es decir multiplicando20′ (1 ancho) por el coeficiente45′:20′ 45′subir,15′ ya ves.
Al final, se elimina la contribución del ancho de45′ (ya escrito 30^ {15}, es decir, como la suma de30′ y15′, de acuerdo con la partición memorizada al final de la línea 7). 30′permanece, es decir, la longitud:15′ desde 30 15′ arranca,30′ ya ves,30′ la longitud.
Con todo, una agradable explicación pedagógica, que guía al alumno de la mano entrecruza a través de la asignatura “cómo transformar una ecuación de primer grado, y cómo entender lo que sucede”.
Antes de dejar el texto, podemos detenernos en los actores que aparecen, y que se repiten en la mayoría de aquellos textos que señalan un problema junto con el procedimiento que conduce a su solución. 5 En primer lugar, una “voz” que habla en primera persona singular describe la situación que ha establecido, y formula la pregunta. A continuación una voz diferente se dirige al alumno, dando órdenes en el imperativo o en la segunda persona singular, en tiempo presente; esta voz no puede ser idéntica a la que planteó el problema, ya que muchas veces la cita en tercera persona, “ya que ha dicho”.
En un contexto escolar, uno puede imaginar que la voz que afirma el problema es la del maestro de la escuela, y que la que se dirige al alumno es un asistente o instructor— “textos edubba”, 6 textos literarios sobre la escuela y sobre la vida escolar, a menudo se refieren a un” hermano mayor” cuya tarea es dar instrucciones. No obstante, el origen del esquema parece ser diferente. Ciertos textos de principios del siglo XVIII comienzan “Si alguien te pregunta así, 'tengo... '”. En estos textos el que pregunta es una persona hipotética que no pertenece a la situación didáctica, pretexto para un acertijo matemático. El guía anónimo es entonces el maestro, originalmente probablemente para ser identificado con un maestro-topógrafo explicando los métodos del oficio a su aprendiz.


