3.3: YBC 6967

Última actualización
Guardar como PDF

Page ID: 109648

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Obv.

1 El igibûm sobre el igûm, 7 va más allá

2 igûm e igibûm qué?

3 Usted, 7 que el igibûm

4 sobre el igûm va más allá

5 a dos descansos:\(3^{\circ} 30^{\prime}\);

6\(3^{\circ} 30^{\prime}\) junto con\(3^{\circ} 30^{\prime}\)

7 hacer bodega:\(12^{\circ} 15^{\prime}\).

8 A\(12^{\circ} 15^{\prime}\) lo que viene para ti

9\(1^{\prime}\) la superficie se une:\(1^{\prime} 12^{\circ} 15^{\prime}\).

10 ¿El igual de\(1^{\prime} 12^{\circ} 15^{\prime}\) qué? \(8^{\circ} 30^{\prime}\).

11\(8^{\circ} 30^{\prime}\) y\(8^{\circ} 30^{\prime}\), su contraparte, se acostó.

Rev.

1\(3^{\circ} 30^{\prime}\), el hecha-hold,

2 de una lágrima,

3 a uno unirse.

4 El primero es 12, el segundo es 5.

5 12 es el igibûm, 5 es el igûm.

Los problemas de segundo grado que tratan los rectángulos son más copiosos que los de los cuadrados. Dos tipos de problemas pertenecen a esta categoría; otros, más complejos, pueden reducirse a estos tipos básicos. En uno de estos se conoce el área y la suma de los lados; en el otro, se da el área y su diferencia.

El ejercicio anterior pertenece a este último tipo, si descuidamos el hecho de que no trata en absoluto de un rectángulo sino de un par de números que pertenecen juntos en la tabla de reciprocales (ver página 20 y figura 1.2). Igûm es la pronunciación babilónica de igi sumerio, e igibûm la de igi.bi, “su igi” (la relación entre los dos es ciertamente simétrica: si\(10^{\prime}\) es igi 6, entonces 6 es igi\(10^{\prime}\)).

Se podría esperar que el producto de igûm e igibûm sea 1; en el problema actual, sin embargo, este no es el caso, aquí se supone que el producto es\(1^{\prime}\), es decir, 60. Los dos números están representados por los lados de un rectángulo de área\(1^{\prime}\) (ver línea Obv. 9); la situación se representa en la Figura 3.4, A. Una vez más tenemos que ver con un rectángulo con área conocida y diferencia conocida entre la longitud y la anchura, respectivamente\(1^{\prime}\) y 7.

Figura\(3.4\): El procedimiento de YBC 6967

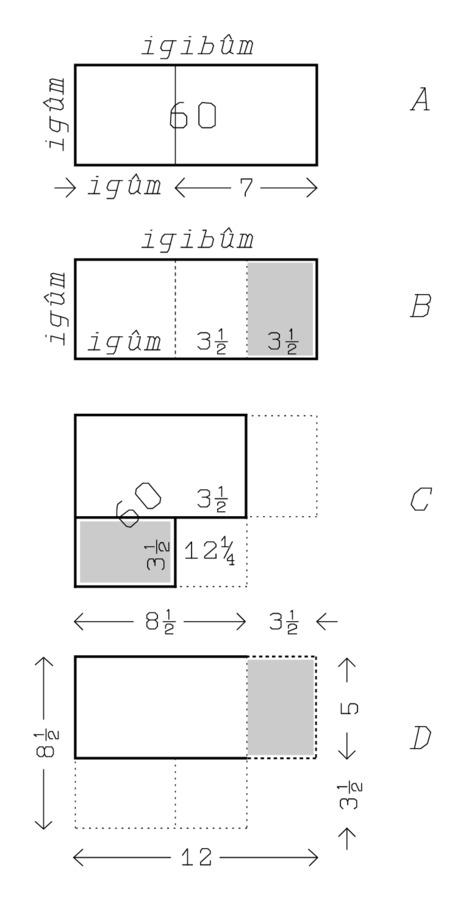
Es importante notar que aquí la “representación fundamental” (las cantidades geométricas medibles) sirve para representar magnitudes de un tipo diferente: los dos números igûm e igibûm. En nuestro álgebra, la situación es la inversa: nuestra representación fundamental la proporciona el reino de los números abstractos, que sirve para representar magnitudes de otro tipo: precios, pesos, velocidades, distancias, etc. (ver página 16).

Al igual que en los dos casos análogos que preceden, el rectángulo se transforma en un gnomón, y como suele ser el gnomón se completa como un cuadrado “sostenido” por los dos “fracciones” del exceso (líneas Obv. 3—10). El procedimiento se puede seguir en las Figuras 3.4, B y 3.4, C.

Los siguientes pasos son notables. El “resto” que se desprendió y se movió alrededor (el “heche-hold”, es decir, el que se “hizo sostener” el cuadrado complementario) en la formación del gnomon se vuelve a colocar en su lugar. Al tratarse de la misma pieza a la que se refiere, en principio debe estar disponible antes de que pueda ser “unida”. Eso tiene dos consecuencias. En primer lugar, el “igual”\(8^{\circ} 30^{\prime}\) debe ser “establecido” ³ dos veces, como vemos en la Figura 3.4, D: de esta manera, la pieza puede ser “arrancada” de una (dejando el ancho igûm) y “unida” a la otra (dando la longitud igibûm) . En segundo lugar, el “desgarro” debe preceder a la “unión” (líneas Av. 1—3), aunque los babilonios (como nosotros) normalmente preferirían sumar antes de restar—cf. BM 13901 #1 —2: el primer problema suma el lado, el segundo resta:\(3^{\circ} 30^{\prime}\), la retención hecha, de una lágrima, a una unión.

En BM 13901 #1 y #2, el complemento se “unió” al gnomón, aquí está el gnomón que se “une”. Dado que ambos permanecen en su lugar, cualquiera de los dos es posible. Cuando\(3^{\circ} 30^{\prime}\) se une\(8^{\circ} 30^{\prime}\) en la construcción del igibûm, este no es el caso: si una magnitud permanece en su lugar y la otra se desplaza siempre es esta última la que se “une”. A diferencia de nuestra adición y el “amontonamiento” de los babilonios, “unirse” no es una operación simétrica.