3.4: BM 13901 #10

Última actualización
Guardar como PDF

Page ID: 109661

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Obv. II

11 Las superficies de mis dos confrontaciones las he colmado:\(21^{\circ} 15^{\prime}\).

12 Confrontación (comparada) con la confrontación, la séptima se ha vuelto más pequeña.

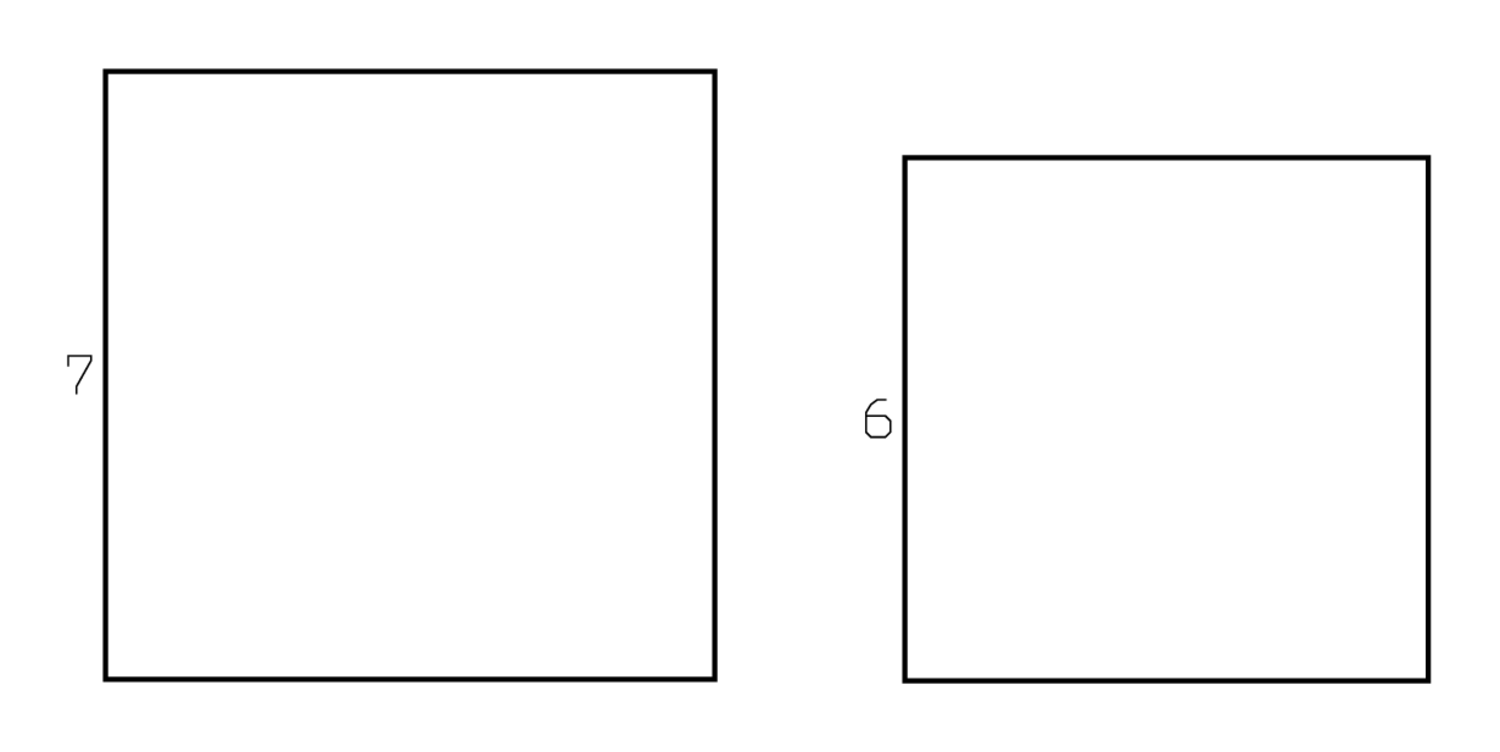
13 7 y 6 te inscribes. 7 y 7 haces bodega, 49.

14 6 y 6 haces bodega, 36 y 49 te apila:

15\(1‵25\). igi no\(1‵25\) está desapegado. Qué\(1‵25\)

16 ¿Puedo postular lo que me\(21^{\circ} 15^{\prime}\) da? Por\(30^{\prime}\),\(30^{\prime}\) es igual.

De 17\(30^{\prime}\) a 7 levantas:\(3^{\circ} 30^{\prime}\) el primer enfrentamiento.

18\(30^{\prime}\) a 6 levantas: 3 el segundo enfrentamiento.

Ahora volvemos a la tableta que contiene una colección de problemas sobre los cuadrados, mirando uno de los problemas más simples sobre dos cuadrados. Las líneas 11 y 12 contienen la declaración: se dice que la suma de las dos áreas sea\(21^{\circ} 15^{\prime}\), y se nos dice que el segundo “enfrentamiento” no llega a la primera por un séptimo. ⁴ En símbolos, si los dos lados están designados respectivamente\(c_{1}\) y\(c_{2}\):

\(\square\left(c_{1}\right)+\square\left(c_{2}\right)=21^{\circ} 15^{\prime} \quad, \quad c_{2}=c_{1}-\frac{1}{7} c_{1}\).

Formulado de manera diferente, la relación entre los dos lados es de 7 a 6. Esta es la base para una solución basada en una “posición falsa” (ver página 32). Las líneas 13 y 14 prescriben la construcción de dos “cuadrados modelo” con lados 7 y 6 (haciendo que estos lados se “sostengan”, ver Figura 3.5), y encuentra que su área total será\(49+36=1^{`} 25\). De acuerdo con el enunciado, sin embargo, el total debería ser\(21^{\circ} 15^{\prime}\); por lo tanto, la superficie debe reducirse por un factor\(21^{\circ} 15^{\prime} / 1^{`} 25\). Ahora no\(1^{`} 25\) hay un número “regular” (ver página 21) —es decir, no tiene igi: igi no\(1^{`} 25\) está separado. Debemos así sacar el cociente “de las mangas"—como se hace en las líneas 15-16, donde se dice que está\(15^{\prime}\) (es decir,\(\frac{1}{4}\)). Sin embargo, si el área se reduce en un factor\(15^{\prime}\), entonces los lados correspondientes deben reducirse por un factor\(30^{\prime}\): Por\(15^{\prime}\),\(30^{\prime}\) es igual. Queda finalmente (líneas 17 y 18) para “elevar” 7 y 6 a\(30^{\prime}\).

El primer “enfrentamiento” resulta así ser\(7 \cdot 30^{\prime}=3^{\circ} 30^{\prime}\), y el segundo\(6 \cdot 30^{\prime}=3\). ⁵

Figura\(3.5\): Los dos cuadrados de BM 13901 #10.