3.5: BM 13901 #14
- Page ID
- 109674
Obv. II
44 Las superficies de mis dos confrontaciones las he colmado:\(25^{\prime} 25^{\prime \prime}\).
45 El enfrentamiento, dos tercios del enfrentamiento y\(5^{\prime}\),\(\mathrm{NINDAN}\).
46 1 y\(40^{\prime}\) y\(5^{\prime}\) sobrepasando\(40^{\prime}\) te inscribes.
47\(5^{\prime}\) y\(5^{\prime}\) te aferras,\(25^{\prime \prime}\) dentro\(25^{\prime} 25^{\prime \prime}\) te arrancas:
Rev. I
1\(25^{\prime}\) te inscribes. 1 y 1 haces bodega, 1. \(40^{\prime}\)y\(40^{\prime}\) te aferras,
2\(26^{\prime} 40^{\prime \prime}\) a 1 te unes:\(1^{\circ} 26^{\prime} 40^{\prime \prime}\) a\(25^{\prime}\) levantas:
3\(36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\) te inscribes. \(5^{\prime}\)a\(40^{\prime}\) que subas:\(3^{\prime} 20^{\prime \prime}\)
4 y\(3^{\prime} 20^{\prime \prime}\) te aferras,\(11^{\prime \prime} 6^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\) a\(36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\) que te unes:
5 por\(36^{\prime} 17^{\prime \prime} 46^{\prime \prime \prime} 40^{\prime \prime \prime}\),\(46^{\prime} 40^{\prime \prime}\) es igual. \(3^{\prime} 20^{\prime \prime}\)que has hecho
6 adentro\(46^{\prime} 40^{\prime \prime}\) arrancas:\(43^{\prime} 20^{\prime \prime}\) te inscribes.
7 igi no\(1^{\circ} 26^{\prime} 40^{\prime \prime}\) está desapegado. Qué\(1^{\circ} 26^{\prime} 40^{\prime \prime}\)
8 ¿Puedo postular lo que me\(43^{\prime} 20^{\prime \prime}\) da? \(30^{\prime}\)su bandûm.
Del 9\(30^{\prime}\) al 1 se plantea:\(30^{\prime}\) el primer enfrentamiento.
10\(30^{\prime}\) a\(40^{\prime}\) que subas:\(20^{\prime}\), y\(5^{\prime}\) te unes a:
11\(25^{\prime}\) el segundo enfrentamiento.
Incluso este problema se ocupa de dos cuadrados (líneas Obv. II.44—45). 6 La formulación algo oscura en la línea 45 significa que el segundo “enfrentamiento” equivale a dos tercios de la primera, con adicional\(5^{\prime} \mathrm{NINDAN}\). Si\(c_{1}\) y\(c_{2}\) representa los dos “enfrentamientos”, la línea 44 nos informa que la suma de las áreas es\(\square\left(c_{1}\right)+\square\left(c_{2}\right)=25^{\prime} 25^{\prime \prime}\), mientras que la línea 45 lo señala\(c_{2}=40^{\prime} \cdot c_{1}+5^{\prime}\).
Este problema no puede resolverse por medio de una simple posición falsa en la que se asume provisionalmente un número hipotético como el valor de lo desconocido, que sólo funciona para problemas homogéneos. 7 Los números 1 y\(40^{\prime}\) en la línea 46 nos muestran la manera que realmente se elige:\(c_{1}\) y\(c_{2}\) se expresan en términos de una nueva magnitud, a la que podemos llamar\(c\):
\(c_{1}=1 \cdot c \quad, \quad c_{2}=40^{\prime} \cdot c+5^{\prime}\).
Eso corresponde a la Figura 3.6. Muestra cómo el problema se reduce a uno más simple tratando con un solo cuadrado\(\square(c)\). Es claro que el área del primero de los dos cuadrados originales (\(\square\left(c_{1}\right)\)) es igual\((1 \times 1) \square(c)\), pero ese cálculo tiene que esperar hasta la línea Rev. I.1. El texto comienza por considerar\(\square\left(c_{2}\right)\), que es más complicado y da lugar a varias aportaciones. Primero, el cuadrado\(\square\left(5^{\prime}\right)\) en la esquina inferior derecha:\(5^{\prime}\) y\(5^{\prime}\) haces bodega,\(25^{\prime \prime}\). Esta contribución se elimina de la suma\(25^{\prime} 25^{\prime \prime}\) de las dos áreas:\(25^{\prime \prime}\) dentro\(25^{\prime} 25^{\prime \prime}\) arrancas:\(25^{\prime}\) te inscribes. Lo\(25^{\prime}\) que queda ahora debe explicarse en términos de la zona y el costado de la nueva plaza\(\square(c)\).
\(\square\left(c_{1}\right)\), como ya se dijo, es\(1 \times 1=1\) veces el área\(\square(c)\): 1 y 1 haces bodega, 1. 8 Después de la eliminación de los\(5^{\prime} \times 5^{\prime}\) restos de\(\square\left(c_{2}\right)\) esquina de, por un lado\(\square\left(40^{\prime} c\right)\), un cuadrado, por el otro, dos “alas” a las que regresaremos inminentemente. El área de la plaza\(\square\left(40^{\prime} c\right)\) es\(\left(40^{\prime} \times 40^{\prime}\right) \square(c)=26^{\prime} 40^{\prime \prime} \square(c)\):\(40^{\prime}\) y\(40^{\prime}\) haces bodega,\(26^{\prime} 40^{\prime \prime}\). En total tenemos así\(1+26^{\prime} 40^{\prime \prime}=1^{\circ} 26^{\prime} 40^{\prime \prime}\) tiempos el área cuadrada\(\square(c)\):\(26^{\prime} 40^{\prime \prime}\) a 1 te unes:\(1^{\circ} 26^{\prime} 40^{\prime \prime}\).
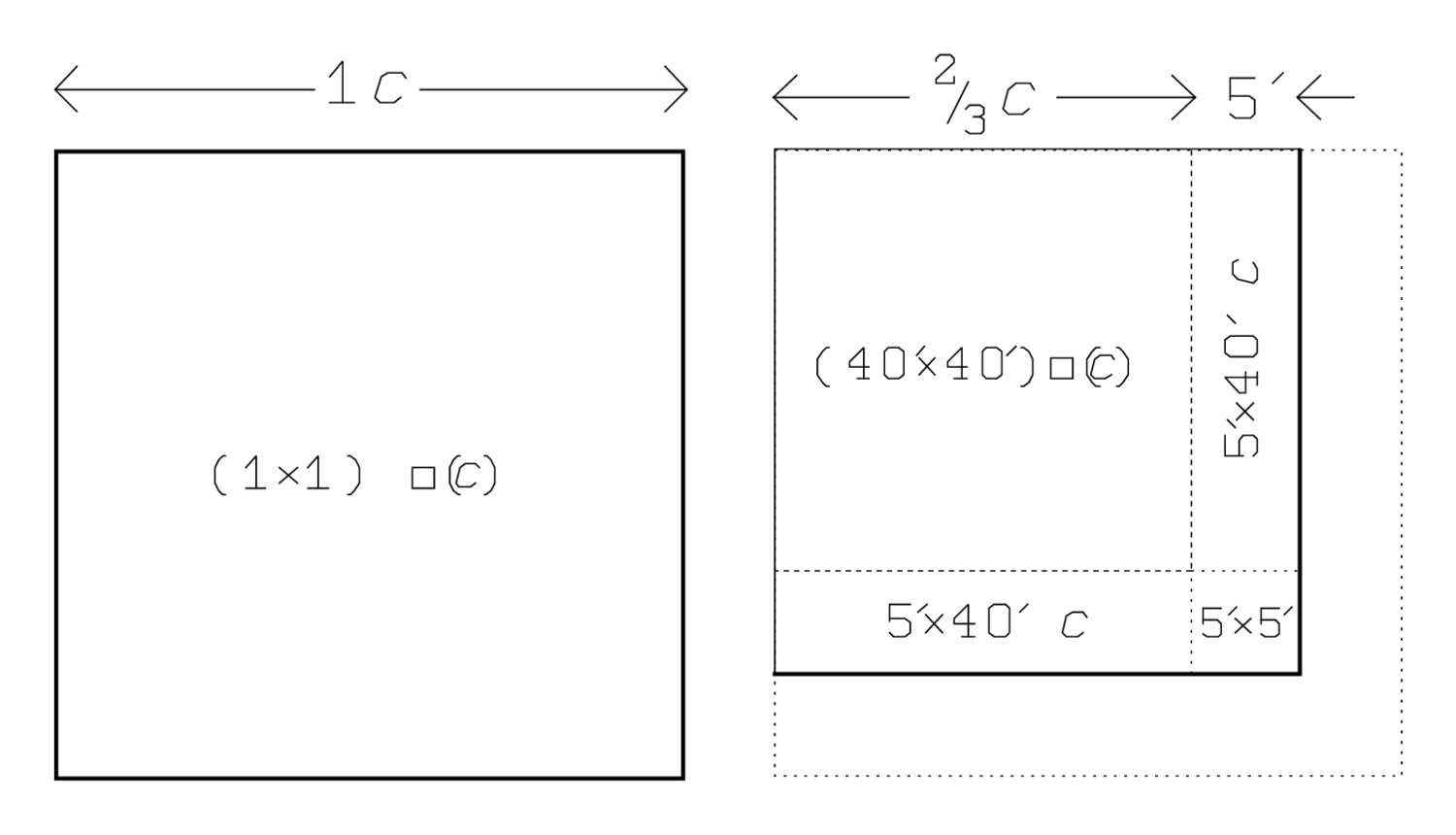
Cada “ala” es un rectángulo (\(5^{\prime}, 40^{\prime}c\), cuya área se puede escribir\(5^{\prime} \cdot 40^{\prime} c=3^{\prime} 20^{\prime \prime} c\):\(5^{\prime}\) a\(40^{\prime}\) usted levanta:\(3^{\prime} 20^{\prime \prime}\). En general tenemos así la ecuación
(\(5^{\prime}, 40^{\prime}c\), cuya área se puede escribir\(5^{\prime} \cdot 40^{\prime} c=3^{\prime} 20^{\prime \prime} c\):\(5^{\prime}\) a\(40^{\prime}\) usted levanta:\(3^{\prime} 20^{\prime \prime}\). En general tenemos así la ecuación
\(1^{\circ} 26^{\prime} 40^{\prime \prime} \square(c)+2 \cdot 3^{\prime} 20^{\prime \prime} c=25^{\prime}\)
Esta ecuación nos confronta con un problema que el antiguo autor babilónico ya ha previsto en la línea Rev. I.2, y que le ha llevado a posponer para más tarde el cálculo de las alas. En términos modernos, la ecuación no está “normalizada”, es decir, el coeficiente del término de segundo grado difiere de 1. La vieja calculadora babilónica podría haberlo explicado correspondientemente al afirmar en la terminología del TMS XVI que “tanto como (hay) de superficies” no es una, véase la parte izquierda de la Figura 3.7, donde tenemos una suma de áreas\(\alpha\) cuadradas (el rectángulo blanco ( \(c, \alpha c\))) y\(\beta\) los lados, es decir, el rectángulo sombreado
( \(c, \alpha c\))) y\(\beta\) los lados, es decir, el rectángulo sombreado (\(c, \beta\)), correspondiente a la ecuación
(\(c, \beta\)), correspondiente a la ecuación
\(\alpha \square(c)+\beta c=\Sigma\)
(en el caso real,\(\alpha=1^{\circ} 26^{\prime} 40^{\prime \prime}\),\(\beta=2 \cdot 3^{\prime} 20^{\prime \prime}\),\(\Sigma=25^{\prime}\)). Esto nos impide utilizar directamente nuestro conocido procedimiento de cortar y pegar. “Romper”\(\beta\) y hacer que las dos “fracciones” “sostengan” no nos daría un gnomon.
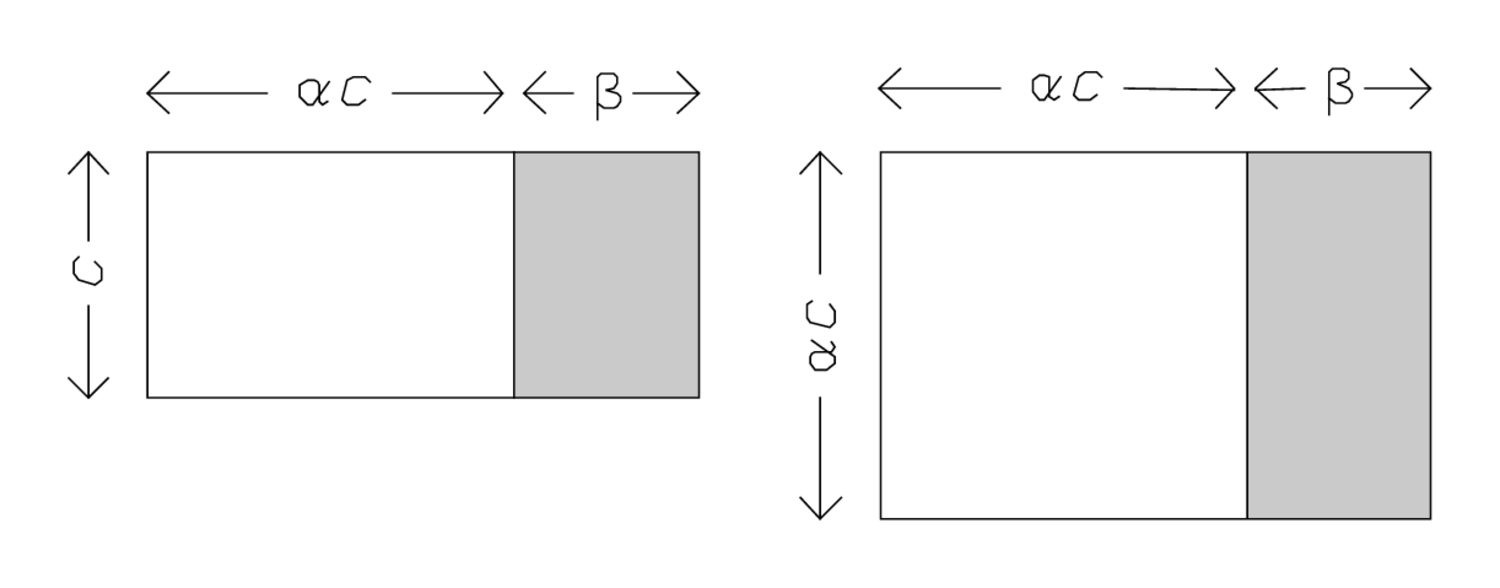
Los babilonios sortearon la dificultad por medio de un dispositivo mostrado en el lado derecho de la figura 3.7: la escala de la configuración se cambia en la dirección vertical, de tal manera que el lado vertical se convierte en\(\alpha c\) lugar de\(c\); en consecuencia, la suma de la dos áreas ya no es\(\Sigma\left(=25^{\prime}\right)\) sino\(\alpha \Sigma\left(=1^{\circ} 26^{\prime} 40^{\prime \prime} \cdot 25^{\prime}=36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\right)\):\(1^{\circ} 26^{\prime} 40^{\prime \prime}\) a\(25^{\prime}\) ti levantas:\(36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\) te inscribes. Como vemos, el número\(\beta\) de lados no se cambia en la operación, sólo el valor del lado, es decir, de\(c\) hacia\(\alpha c\). 9
En el lenguaje simbólico moderno, esta transformación corresponde a una multiplicación de los dos lados de la ecuación
\(\alpha c^{2}+\beta c=\Sigma\)
por\(\alpha\), lo que nos da una ecuación normalizada con lo desconocido\(\alpha c\):
\((\alpha c)^{2}+\beta \cdot(\alpha c)=\alpha \Sigma\),
una ecuación del tipo que hemos encontrado en BM 13901 #1. Por lo tanto, hemos llegado a un punto en el que podemos aplicar el método habitual: “romper” el rectángulo sombreado y hacer que los dos “restos” resultantes “sostengan” un complemento cuadrático (Figura 3.8); el “resto” externo está ligeramente sombreado en su posición original y más fuertemente en la posición de que se trae). Ahora, y solo ahora, la calculadora necesita conocer el número de lados en el rectángulo sombreado de la Figura 3.7 (es decir, para determinar\(\beta\)). Como ya se dijo, cada “ala” aporta\(5^{\prime} 40^{\prime \prime}=3^{\prime} 20^{\prime \prime}\) lados. Si la calculadora hubiera funcionado mecánicamente, según algoritmos fijos, ahora se habría multiplicado por 2 para poder encontrar\(beta\). ¡Pero no lo hace! Él sabe efectivamente que las dos alas constituyen el exceso que tiene que ser “roto” en dos “fracciones”. Por lo tanto, hace\(3^{\prime} 20^{\prime \prime}\) y\(3^{\prime} 20^{\prime \prime}\) “sostiene” directamente, lo que produce el complemento cuadrático, y “une” el área resultante\(11^{\prime \prime} 6^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\) a la del gnomón\(36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\):\(3^{\prime} 20^{\prime \prime}\) y\(3^{\prime} 20^{\prime \prime}\) haces bodega,\(11^{\prime \prime} 6^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\) a \(36^{\prime} 6^{\prime \prime} 40^{\prime \prime \prime}\)te unes a: [...] \(36^{\prime} 17^{\prime \prime} 46^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\).
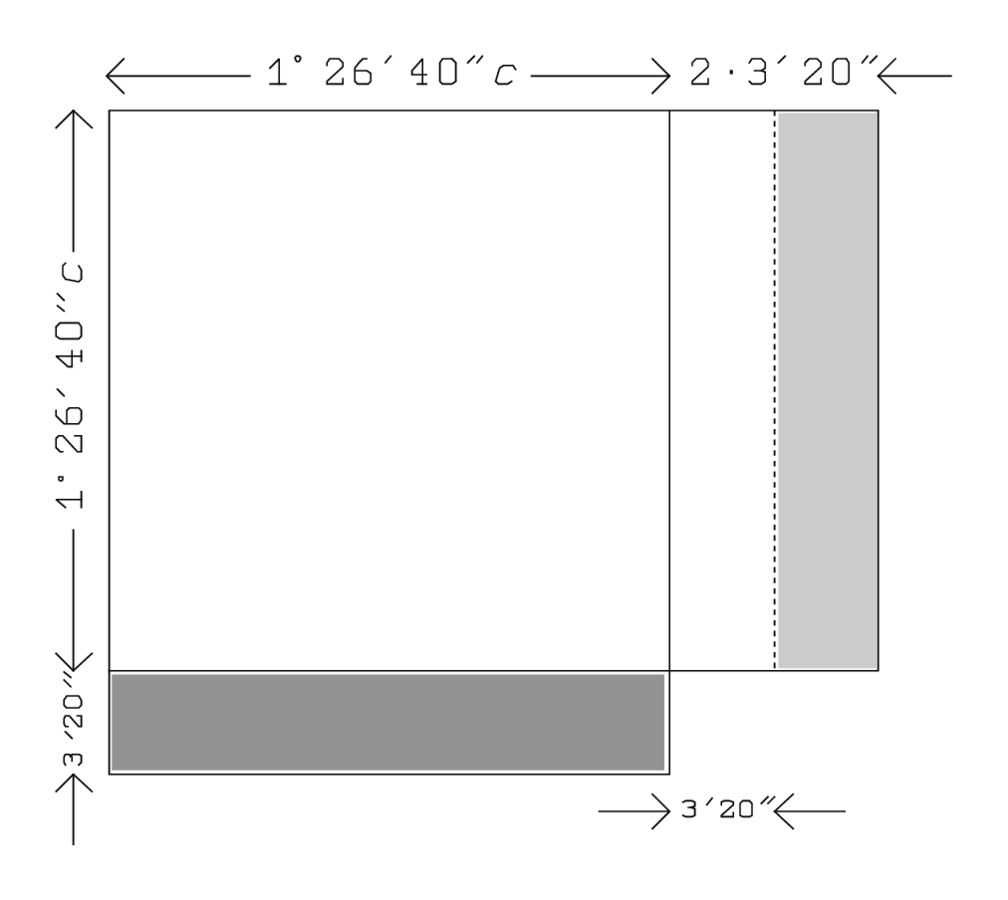
\(36^{\prime} 17^{\prime \prime} 46^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\)es así el área de la plaza terminada, y su lado\(\sqrt{36^{\prime} 17^{\prime \prime} 46^{\prime \prime \prime} 40^{\prime \prime \prime \prime}}=46^{\prime} 40^{\prime \prime}\): by\(36^{\prime} 17^{\prime \prime} 46^{\prime \prime \prime} 40^{\prime \prime \prime \prime}\),\(46^{\prime} 40^{\prime \prime}\) es igual. Este número representa\(1^{\circ} 26^{\prime} 40^{\prime \prime} \cdot c+3^{\prime} 20^{\prime \prime}\); por lo tanto,\(1^{\circ} 26^{\prime} 40^{\prime \prime} c\) es\(46^{\prime} 40^{\prime \prime}-3^{\prime} 20^{\prime \prime}=43^{\prime} 20^{\prime \prime}\):\(3^{\prime} 20^{\prime \prime}\) que has hecho\(46^{\prime} 40^{\prime \prime}\) aferrarte dentro arrancas:\(43^{\prime} 20^{\prime \prime}\) te inscribes. A continuación, debemos encontrar el valor de\(c\). \(1^{\circ} 26^{\prime} 40^{\prime \prime}\)es un número irregular, y el cociente\(46^{\prime} 40^{\prime \prime} / 1^{\circ} 26^{\prime} 40^{\prime \prime}\) se da directamente como\(30^{\prime}\): 10 igi no\(1^{\circ} 26^{\prime} 40^{\prime \prime}\) está separado. ¿Qué\(1^{\circ} 26^{\prime} 40^{\prime \prime}\) puedo postular lo que me\(43^{\prime} 20^{\prime \prime}\) da? \(30^{\prime}\)su bandûm.
Al final,\(c_{1}\) y\(c_{2}\) están determinados,\(c_{1}=1 \cdot c=30^{\prime}\),\(c_{2}=40^{\prime} \cdot c+5^{\prime}=25^{\prime}\): 11\(30^{\prime}\) a 1 levantas:\(30^{\prime}\) el primer enfrentamiento. \(30^{\prime}\)a\(40^{\prime}\) levantarte:\(20^{\prime}\) y\(5^{\prime}\) te unes:\(25^{\prime}\) el segundo enfrentamiento. El problema está resuelto.


