3.6: TMS IX #1 y #2

Última actualización
Guardar como PDF

Page ID: 109685

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

#1

1 La superficie y 1 longitud he colmado,\(40^{\prime}\). ^¿30, la longitud,^?\(20^{\prime}\)el ancho.

2 Como 1 longitud a\(10^{\prime}\) la superficie, se ha unido,

3 o 1 (como) base a\(20^{\prime}\), el ancho, se ha unido,

4 o\(1^{\circ} 20^{\prime}\) ′ ^¿se postula^?a la anchura que\(40^{\prime}\) junto con la longitud ^¿sostiene^?

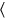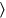5 o\(1^{\circ} 20^{\prime}\) toge alt ther alt con\(30^{\prime}\) la longitud sostiene,\(40^{\prime}\) (es) su nombre.

6 Ya que así, a\(20^{\prime}\) la anchura, que se le dice,

7 1 se une:\(1^{\circ} 20^{\prime}\) ya ves. Fuera de aquí

8 usted pregunta. \(40^{\prime}\)la superficie,\(1^{\circ} 20^{\prime}\) el ancho, el largo ¿qué?

9\(30^{\prime}\) la longitud. De ahí el procedimiento.

#2

10 Superficie, largo y ancho que he colmado, 1. Por el acadio (método).

11 1 a la unión de longitud. 1 a la unión de ancho. Dado que 1 a la longitud se une,

12 1 a la anchura se une, 1 y 1 hacen sujeción, 1 ya ves.

13 1 al montón de longitud, ancho y unión de superficie, 2 ya ves.

14 A\(20^{\prime}\) la anchura, 1 unirse,\(1^{\circ} 20^{\prime}\). A\(30^{\prime}\) la longitud, 1 unirse,\(1^{\circ} 30^{\prime}\).

15 ^¿Desde^?una superficie, la de\(1^{\circ} 20^{\prime}\) la anchura, la de\(1^{\circ} 30^{\prime}\) la longitud,

16 ^¿la longitud junto con^?el ancho, se hacen bodega, ¿cuál es su nombre?

17 2 la superficie.

18 Así el acadio (método).

Como TMS XVI #1, las secciones #1 y #2 del presente texto no resuelven ningún problema. ¹² En cambio, ofrecen una explicación pedagógica del significado a atribuir a la adición de áreas y líneas, y de las operaciones utilizadas para tratar problemas de segundo grado. Las Secciones #1 y #2 establecen dos situaciones distintas. En #1, se nos dice la suma del área y la longitud de un rectángulo; en #2, se da la suma de área, longitud y anchura. #3 (que se tratará en el siguiente capítulo) es entonces un problema genuino que se afirma y resuelve de acuerdo con los métodos enseñados en #1 y #2 y en TMS XVI #1.

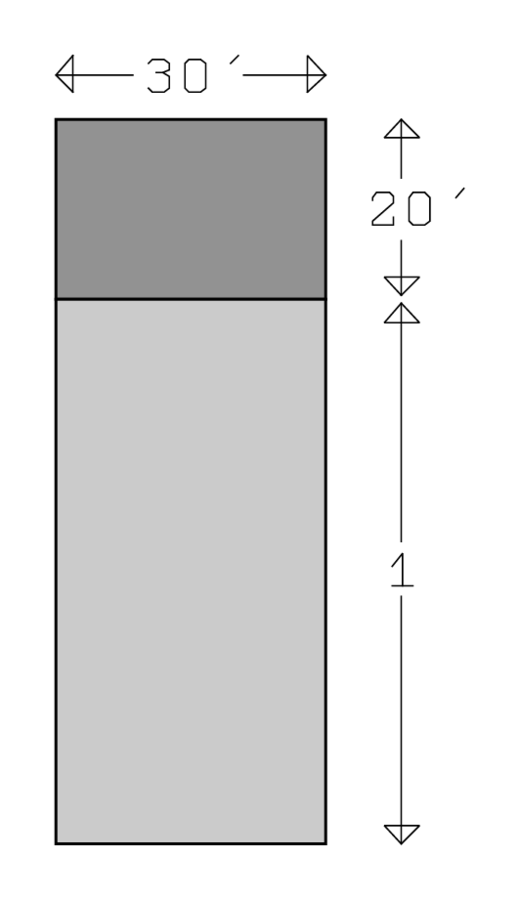
La figura (3.9) se dibuja de acuerdo con el texto de #1, en el que se conoce la suma de un área rectangular y la longitud correspondiente. Paralelamente a nuestra transformación simbólica

\(\ell \cdot w+\ell=\ell \cdot w+\ell \cdot 1=\ell \cdot(w+1)\),

el ancho se extiende por una “base”. ¹³ Eso lleva a toda una secuencia de explicaciones, mutuamente dependientes y unidas por “o... o... o”, curiosamente similar a como hablamos de las transformaciones de una ecuación, por ejemplo

\(" 2 a^{2}-4=4, \quad \text { or } \quad 2 a^{2}=4+4, \quad \text { or } \quad a^{2}=4, \quad \text { or } \quad a=\pm \sqrt{4}=\pm 2^{\prime \prime}\).

La línea 2 habla de la “superficie” como\(10^{\prime}\). Esto demuestra que se supone una vez más que el alumno sepa que la discusión trata del rectángulo alt (\(30^{\prime}\),\(20^{\prime}\)). La tablilla está rota, por lo que no podemos saber si la longitud se declaró explícitamente, pero la cita en la línea 6 muestra que el ancho estaba.

Al final, las líneas 7-9 muestran cómo encontrar la longitud una vez que se conoce el ancho junto con la suma de área y longitud (mediante una división que permanece implícita).

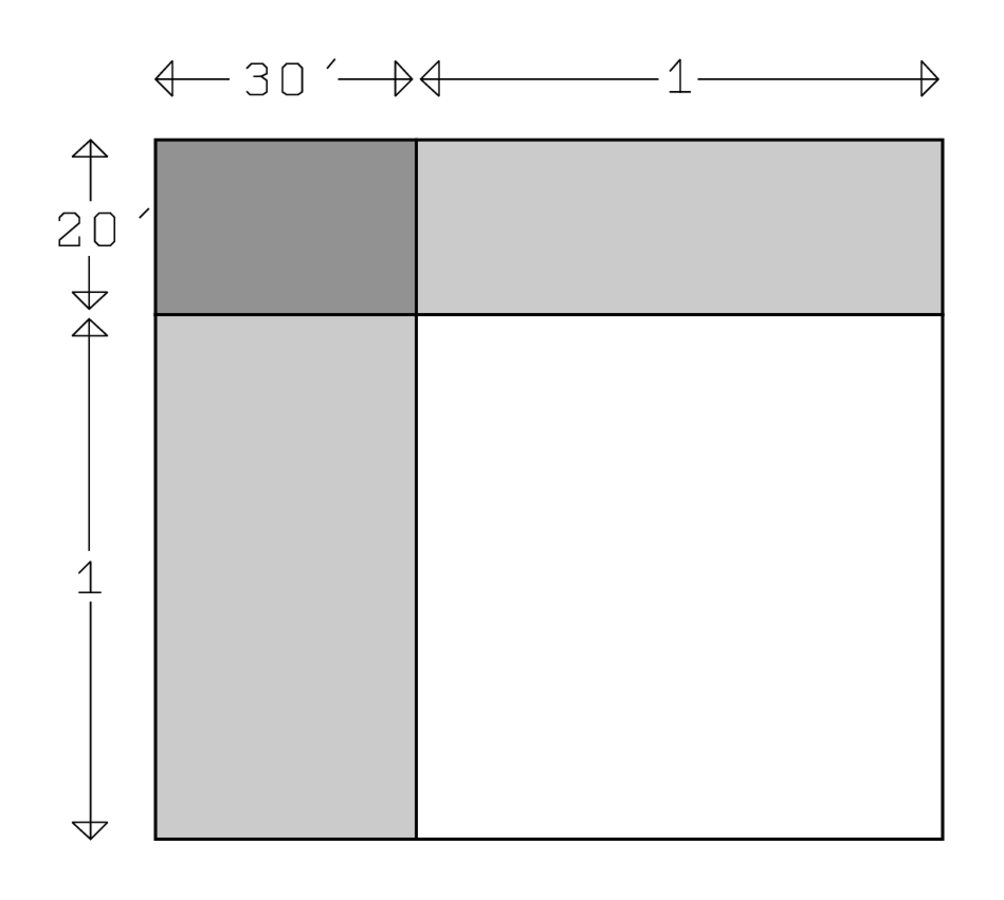
#2 enseña cómo enfrentar una situación más compleja; ahora se da la suma del área y ambos lados (Figura 3.10). Tanto el largo como el ancho se prolongan en 1; eso produce dos rectángulos alt (\(\ell\),1) y alt (\(w\),1), cuyas áreas, respectivamente, son la longitud y la anchura. Pero también produce una esquina cuadrada vacía alt (1,1). Cuando se llena tenemos un rectángulo mayor de largo\(\ell+1\left(=1^{\circ} 30^{\prime}\right)\), ancho\(w+1\left(=1^{\circ} 20^{\prime}\right)\) y área\(1+1=2\); una comprobación confirma que el rectángulo “sostenido” por estos dos lados es efectivamente del área 2.

Este método tiene un nombre, lo cual es muy raro en las matemáticas babilónicas antiguas (o al menos en sus huellas escritas). Se llama “el acadio (método)”. “acadio” es la designación común de la lengua cuyos principales dialectos son babilónicos y asirios (véase el recuadro “Rudimentos de la historia general”), y también del mayor componente no sumerio de la población durante el tercer milenio; hay evidencia (parte de la cual está constituida por el presente texto) que la vieja escuela de escribas babilónicos se inspiró para su “álgebra” a partir de la práctica de una profesión acadio de topógrafos (discutiremos este tema en la página 108). El método “acadio” no es más que una terminación cuadrática aunque sea una variante ligeramente atípica, es decir, la herramienta básica para la solución de todos los problemas mixtos de segundo grado (ya sean geométricos o, como con nosotros, expresados en álgebra numérica); y es precisamente esta herramienta básica la que es caracterizado como el “acadio (método).