4.2: AO 8862 #2
- Page ID
- 109547
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)I
30 Largo, ancho. Largo y ancho
31 He hecho bodega: Una superficie que he construido.
32 Me di la vuelta (eso). La mitad de la longitud
33 y el tercero de la anchura
34 al interior de mi superficie
35 Me he sumado: 15.
36 Me di la vuelta. Largo y ancho
37 He colmado: 7.
II
1 ¿Largo y ancho qué?
2 Usted, por su procedimiento,
3 2 (as) inscripción de la mitad
4 y 3 (como) inscripción
5 de la tercera te inscribe:
6 igi 2,\ (30^ {\ prime}\, desacoplas:
7\(30^{\prime}\ steps of 7, \(3^{\circ} 30^{\prime}\); a 7,
8 las cosas colmadas, largo y ancho,
9 Traigo:
10\(3^{\circ} 30^{\prime}\) de 15, mis cosas colmadas,
11 corte:
12\(11^{\circ} 30^{\prime}\) el resto.
13 No vayas más allá. 2 y 3 hacen bodega:
14 3 pasos de 2, 6.
15 igi 6,\ (10^ {\ prime}\ te da.
16\ (10^ {\ prime}\ de 7, tus cosas colmadas,
17 de largo y ancho, arranco:
18\(6^{\circ} 50^{\prime}\) el resto.
19 Su resto, el de\(6^{\circ} 50^{\prime}\), rompo:
20\(3^{\circ} 25^{\prime}\) te da.
21\(3^{\circ} 25^{\prime}\) hasta dos veces
22 te inscribe;\(3^{\circ} 25^{\prime}\) pasos de\(3^{\circ} 25^{\prime}\),
23\(11^{\circ} 40^{\prime} 25^{\prime \prime}\); desde el interior
24\(11^{\circ} 30^{\prime}\) Me arranco:
25\(10^{\prime} 25^{\prime \prime}\) el resto.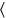 
Por\(10^{\prime} 25^{\prime \prime}\),\(25^{prime}\) es igual
.
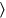26 A la primera\(3^{\circ} 25^{\prime}\)
27\(25^{prime}\) te unes a:\(3^{\circ} 50^{\prime}\),
28 y (aquello) que de las cosas colmadas de
29 de largo y ancho que he arrancado
30 para\(3^{\circ} 50^{\prime}\) unirte a:
31 4 la longitud. A partir de la segunda\(3^{\circ} 25^{\prime}\)
32\(25^{prime}\) Me arranco: 3 el ancho.
33 7 las cosas colmadas.
34 4, la longitud; 3, la anchura; 12, la superficie.
Las dos primeras palabras de la primera línea (I.30) nos dicen que estamos ante una figura que se caracteriza completamente por su longitud y su anchura, es decir, con un rectángulo (cf. página 28) —o más bien con un campo rectangular: las referencias a la práctica de la agrimensura se pueden encontrar en el texto (por ejemplo, giré a su alrededor en la línea I.32 probablemente significa que el topógrafo, después de haber tendido un campo, ha caminado alrededor de él; en el I.36 se dio la vuelta).
Antes de estudiar el procedimiento, podemos concentrarnos en ciertos aspectos de la formulación del texto. En la línea I.31 vemos que la operación “para aferrarse” no produce de inmediato un resultado numérico —ya que aún se desconocen las medidas de los bandos, eso sí sería difícil. El texto sólo dice que se ha “construido” una “superficie”; probablemente estamos destinados a entender que se ha trazado en el terreno. Posteriormente, cuando dos segmentos conocidos van a “retener” (líneas II.13—14, y quizás II.21—22), la determinación numérica del área aparece como una operación distinta, descrita con las palabras de la tabla de multiplicación. Por último, observamos que el texto define el resultado de una adición “colmada” como plural, traducido “las cosas colmadas”, y que no se respeta el patrón alternante normal de la persona gramatical.
El texto, casi con certeza de Larsa, parece ser de c. 1750 a. C. y así pertenecer a la fase temprana de la adopción del álgebra por parte de la escuela sureña de escribas (ver página 109). Estas particularidades pueden, por lo tanto, darnos información sobre las ideas en las que se basaba; tales ideas iban a ser menos visibles una vez que el lenguaje y el formato se estandarizaran.
El tema del problema es así un rectángulo. Las líneas I.36-37 nos dicen que el “montón” de su largo y ancho es de 7, mientras que las líneas I.32-35 indican que “unir” la mitad de la longitud y un tercio del ancho a la “superficie” produce 15: 2
\((\ell, w)+\frac{1}{2} \ell+\frac{1}{3} w=15 \quad, \quad \ell+w=7\).La solución podría haber seguido el patrón de TMS IX #3 (página 57). Al introducir una “longitud extendida”\(\lambda=\ell+\frac{1}{3}\) y una “anchura extendida”\(\phi=w+\frac{1}{2}\), y agregar (según el “método acadio”) el rectángulo\(\left(\frac{1}{2}, \frac{1}{3}\right)\) que falta en la esquina donde 2 y 3 están “inscritos”, habríamos reducido el problema a
\((\lambda, \phi)=15+\mathrm{C} \sqsupset\left(\frac{1}{2}, \frac{1}{3}\right)=15^{\circ} 10^{\prime}, \lambda+\phi=7+\frac{1}{2}+\frac{1}{3}=7^{\circ} 50^{\prime}\).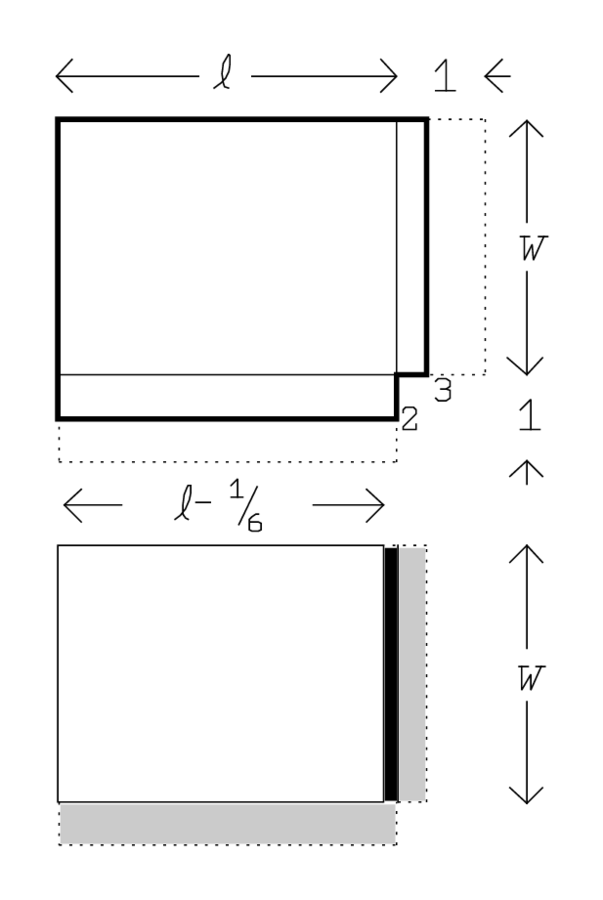
En esta operación, es obvio que se ha eliminado la mitad (sombreada) de la longitud que se había “unido” según el comunicado. Sin embargo, más del tercio (igualmente sombreado) del ancho ha desaparecido. ¿Cuánto más precisamente?
\((3,2)\)(tal vez uno debería imaginarlo en la esquina donde 2 y 3 están “inscritos” en la Figura 4.2; en cualquier caso la Figura 4.3 muestra la situación). Sin más argumento se ve que la mitad (tres cuadrados pequeños) supera al tercero (dos cuadrados pequeños) por uno de seis cuadrados pequeños, es decir, por un sexto, otro caso de razonamiento por “posición falsa”. Excepcionalmente, igi 6 no es “separado” sino “dado” (es decir, por la tabla de reciprocales).Figura\(4.3\)
Sabemos así que, además del tercio del ancho, hemos eliminado una pieza\(\left(w, 10^{\prime}\right)\) (dibujada en negro); si\(\lambda=\ell-10^{\prime}\), por lo tanto, tenemos
\((\lambda, w)=11^{\circ} 30^{\prime}\).Figura\(4.4\)
Por lo tanto, una vez más tenemos un rectángulo del que conocemos el área y la suma de largo y ancho. El procedimiento es el mismo que en la parte final del TMS IX #3 —Figura 4.4; el área que se va a desplazar se muestra nuevamente en sombreado ligero en la posición desde donde se va a tomar y en sombreado pesado donde se tiene que colocar. La única diferencia es terminológica: en TMS IX #3, los dos “restos” son “retenidos”, aquí están “inscritos” —pero como una multiplicación de un número por un número sigue inmediatamente, la construcción habitual de un rectángulo (aquí un cuadrado) debe ser intedneada (líneas II.13-14). 5
Al final, la suma final del lado del cuadrado precede a la resta, como en TMS IX #3. Una vez más, en efecto, no es la misma pieza la que está involucrada en las dos operaciones; por lo tanto, no hay necesidad de ponerla a disposición antes de agregarla.