4.3: IVA 7532
- Page ID
- 109562
Obv.
1 Un trapecio. He cortado una caña. He tomado la caña, por su integridad
2 1 sesenta (a lo largo) el largo me he ido. La 6ta parte
3 rompieron para mí:\(1‵12\) a la longitud que he hecho seguir.
4 Me di la vuelta. La tercera parte y\(\frac{1}{3}\) kùš se rompieron para mí:
5 3 sesenta (a lo largo) el ancho superior me he ido.
6 Con lo que se rompió para mí lo agrandé:
7 36 (a lo largo) el ancho fui. 1 bùr la superficie. La cabeza (magnitud inicial) de la caña ¿qué?
8 Usted, por su procedimiento, (por) la caña que no conoce,
9 1 puede postular. Su sexta parte hacen ruptura,\(50^{\prime}\) te vas.
10 igi\(50^{\prime}\) desprenden,\(1^{\circ} 12^{\prime}\) a 1 sesenta elevar:
11\(1‵12\) para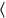
\(1‵12\)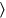
unir:\(2‵24\) la longitud falsa que te da.
12 (Para) la caña que no conoces, 1 puede postular. Su tercera parte hacen ruptura,
13\(40^{\prime}\) a 3 sesenta del aumento de ancho superior:
14\(2‵\) te da. \(2‵\)y 36 el montón de ancho inferior,
15\(2‵36\) a\(2‵24\) la falsa subida de longitud,\(6``14`24\) la superficie falsa.
16 La superficie a 2 repeticiones,\(1``\) para\(6``14`24\) elevar
17\(6````14```24``\) te da. Y\(\frac{1}{3}\) kùš que se rompió
18 a 3 sesenta elevar: 5 a\(2‵24\), la longitud falsa,
19 elevar:\(12‵\). \(\frac{1}{2}\)de\(12‵\) descanso,\(6‵\) hacer encuentro,
Rev.
1\(36``\) para\(6````14```24``\) unirte\(6````15```\), te da.
2 Por\(6````15```\),\(2``30^{\prime}\) es igual. \(6`\)que te queda
3 para\(2``30`\) unirte\(2``36`\), te da. igi\(6``14`24\),
4 la superficie falsa, no lo sé. Qué\(6``14`24\)
5 ¿Puedo postular lo que me\(2``36\) da? \(25^{\prime}\)postular.
6 Desde que la sexta parte se rompió antes,
7 6 inscribe: 1 make go away, 5 te vas.
8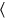
igi 5 despegar,\(12^{\prime}\) a 25 subir\(5^{\prime}\), te da
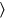. \(5^{\prime}\)para\(25^{\prime}\) unirte:\(\frac{1}{2} \mathrm{NINDAN}\), la cabeza de la caña te da.
Este problema también se refiere a un campo, pero a un campo que el topógrafo solo encontraría en sueños (o mejor dicho, en una pesadilla). “La vida real” entra a través de la referencia a la unidad bùr, una unidad perteneciente a la administración agrícola práctica, y a través de la referencia a medir por medio de un corte de caña para este fin; su longitud (\(\frac{1}{2} \mathrm{NINDAN}\)) corresponde efectivamente a una unidad de medida utilizada a menudo en la vida práctica y llamada precisamente una “caña” (gi en sumerio). También se puede imaginar que tales cañas se romperían fácilmente. Por último, el uso del numeral “sesenta” nos muestra una de las formas de expresar números sin ambigüedades.
Todo lo demás, sin embargo —es decir, que se conozca el área del campo antes de medirla, y también las formas de indicar las medidas de las piezas que se desprenden de la caña— muestra qué artimañas tuvieron que hacer uso los maestros de la vieja escuela babilónica para producir problemas de segundo grado teniendo cierto sabor de vida práctica.
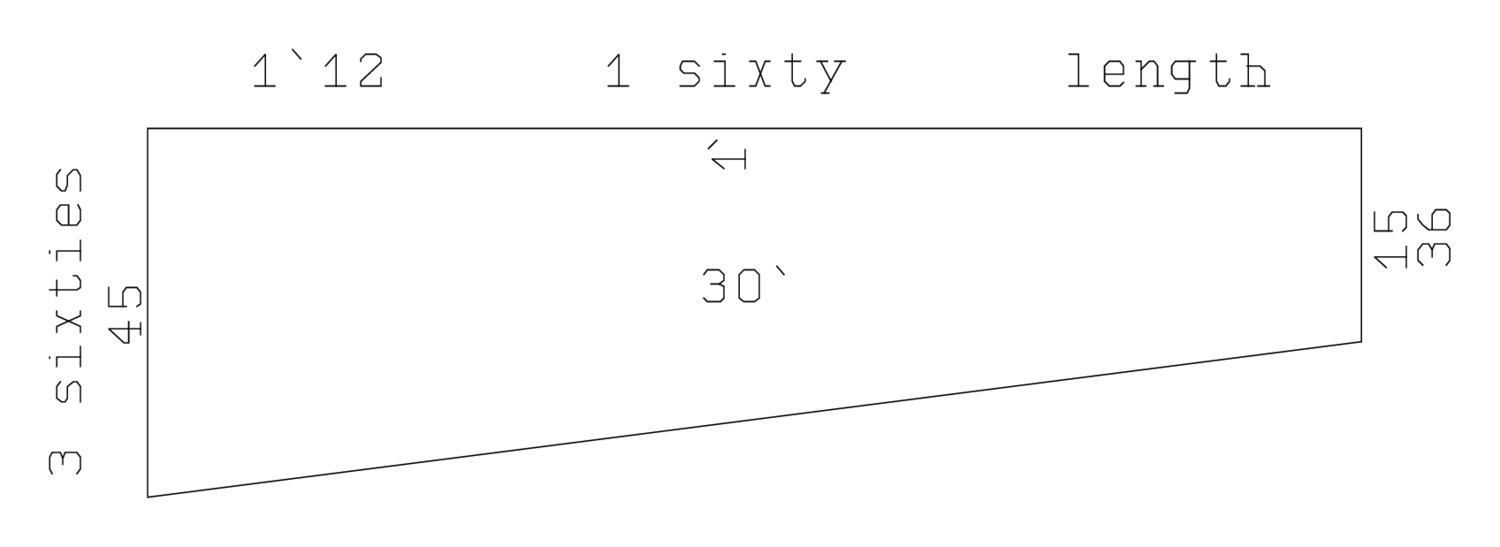
Por una vez, la Figura 4.5 reproduce un diagrama que se traza en la propia tableta. En general, como también aquí, los diagramas sólo se dibujan en las tablillas cuando sirven para aclarar el enunciado; nunca se utilizan para explicar el procedimiento. Por otro lado, la Figura 4.5 muestra una vez más que la solución se conoce de antemano: los números\(1‵\), 45 y 15 son efectivamente las medidas de los lados expresados en\(\mathrm{NINDAN}\).
Así, nos comprometemos a medir el trapecio por medio de una caña de longitud desconocida\(R\). Logramos medir longitudes de\(1`\) caña a lo largo del trapecio antes de que la caña pierda una sexta parte de su longitud y se reduzca a\(r=\frac{5}{6} R\). Lo que queda de la longitud resulta ser\(1^{\prime} 12 r\) (líneas Obv. 2-3).
Después la caña se rompe por segunda ocasión. Según las líneas Obv. 4 y 5, la medida del “ancho superior” (a la izquierda) 6 es\(3` z\), donde\(z=\frac{2}{3} r-\frac{1}{3}\) kùš es la longitud de la caña después de esta segunda reducción.
La pieza que se rompió en último lugar se vuelve a poner en su lugar, y el “ancho (inferior)” (evidentemente a la derecha) se estira (línea Obv. 7) como\(36 r\). Finalmente aprendemos que el área del archivado es 1 bùr =\(30`\) sar (1 sar = 1\(\mathrm{NINDAN}^{2}\)), ver página 17). Se nos pide encontrar la longitud original de la caña, su “cabeza” en el sentido de “principio”.
Las líneas Obv. 9-11 determinan la longitud en unidades\(r\) por medio de una posición falsa: si\(R\) hubiera sido igual a 1, entonces\(r\) habría sido\(50^{\prime}\); a la inversa,\(R\) debe corresponder a\(r\) multiplicar por igi\(50^{\prime}=1^{\circ} 12^{\prime}\). \(1`\)los pasos de\(R\) así corresponden a\(1`12 \cdot r\), y la longitud completa será
\(1` 12 \cdot r+1` 12 \cdot r=2` 24 \cdot r\).
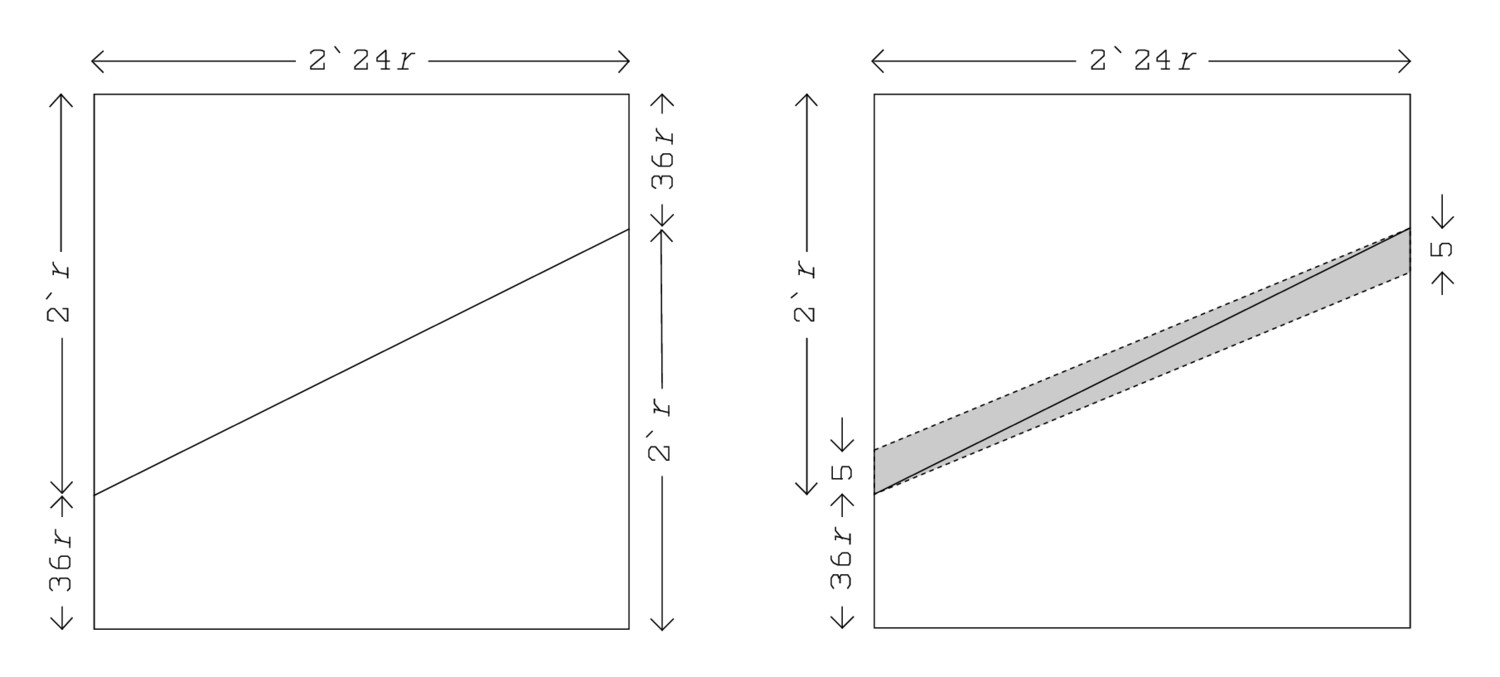
El texto habla\(2`24\) como la “longitud falsa”, es decir, la longitud expresada en unidades\(r\).
Otra posición falsa se aplica en la línea Obv. 12. El texto postula 1 para la longitud\(r\) de la caña una vez acortada, y deduce que lo que queda después de la pérdida de\(\frac{1}{3}\) debe ser igual a\(40^{\prime}\). Dejando a un lado la pérdida extra de\(\frac{1}{3}\) kùš, el falso ancho superior (el ancho superior medido en unidades\(r\)) es\(40^{\prime}\) así por 3 sesenta, es decir,\(40^{\prime} \cdot 3^{\prime}=2`\). En otras palabras, el ancho superior mide\(2` r\) —dejando a un lado la pieza faltante de\(\frac{1}{3}\) kùš.
Dado que la línea Obv. 7 indica que el ancho falso (inferior) es 36, así sabemos—con la misma reserva concerniente a la faltante\(\frac{1}{3}\) kùš—los tres lados que nos permitirán determinar el área del trapecio en unidades\(\square(r)\).
Sin embargo, el texto no calcula esta área: La superficie de 2 repiten. En cambio, dobla el trapecio para formar un rectángulo (ver la parte izquierda de la Figura 4.6), y las líneas Obv. 14—16 calculan el área de este rectángulo (la “superficie falsa”), encontrando\(6``14`24\) (en la unidad implícita\(\square(r)\)).
Si la caña no hubiera perdido una pieza ulterior de\(\frac{1}{3}\) kùš, ahora podríamos haber encontrado la solución por medio de una posición falsa final similar a la de BM 13901 #10 (ver página 46): según la línea Obv. 7, el área del campo es 1 bùr, el área duplicada de ahí 2 bùr =\(1`` \mathrm{NINDAN}^{2}\) (Obv. 16: La superficie a 2 repetir,\(1``\)). Sin embargo, las cosas son más complicadas aquí. Para cada uno de los\(3`\) pasos realizados por la caña dos veces acortada falta en nuestro cálculo un trozo de\(\frac{1}{3}\) kùš, en total así\(3` \cdot \frac{1}{3} \mathrm{kùš}=1` \mathrm{kùš}=5 \mathrm{NINDAN} \left(1 \mathrm{kùš}=\frac{1}{12} \mathrm{NINDAN}\right)\): Y\(\frac{1}{3}\) kùš que se rompió a 3 sesenta subir: 5 (Obv. 17-18). Por lo tanto, el área del campo real no corresponde a lo que vemos a la izquierda en la Figura 4.6 sino a la que queda tras la eliminación de la franja sombreada a la derecha. El área de esta franja es\(5 \cdot 2` 24 r=12` r\):\(5\) a\(2`24\), la longitud falsa, subir:\(12`\). La relación entre la “superficie falsa” y la del trapecio real duplicado ahora se puede expresar mediante la ecuación
\(6``14` 24 \square(r)-12` r=1``\).
Esta ecuación no normalizada se resuelve de la manera habitual. Primero se multiplica por\(6``14` 24\):\(1``\) para\(6``14` 24\) subir te\(6````14```24``\) da (Obv. 16-17). Eso lleva a la ecuación normalizada
\(\square\left(6`` 14` 24 r\right)-12` \cdot\left(6`` 14` 24 r\right)=6```` 14``` 24``\)
o, con\(s=6`` 14` 24 r\)\(r\) como desconocido,
\(\square(s)-12 s=6```` 14``` 24``\).
A partir de aquí, el procedimiento coincide con el de BM 13901 #2 (página 43), con una pequeña variación al final. Los cálculos se pueden seguir en la Figura 4.7.
El área\(6```` 14``` 24``\) corresponde al rectángulo de (altura)\(s\) y anchura\(s-12`\). La mitad del exceso de la altura sobre la anchura se “rompe” y se reposiciona como se ve en el diagrama: ligeramente sombreada en las posiciones originales, fuertemente sombreada donde se mueve. La construcción de la plaza concluyente se describe con uno de los sinónimos de “hacer bodega”, a saber, “hacer encuentro” (Obv. 19).
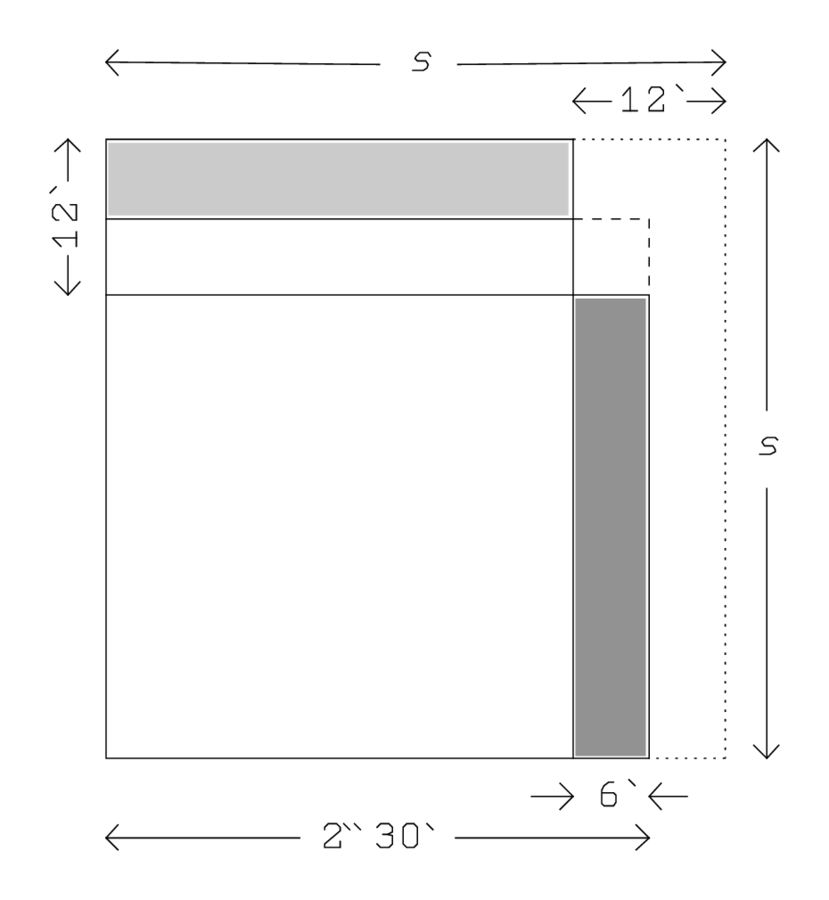
Después de las operaciones habituales nos encontramos con eso\(s=6`` 14` 24 r=2`` 36`\), y en la línea Rev. 5 eso\(r=25^{\prime}\). Observamos, sin embargo, que el “resto” que se movió alrededor no se vuelve a poner en su posición original, lo que se habría reconstituido\(s\) en dirección vertical. En cambio, el otro “resto”, originalmente dejado en su lugar, también se mueve, lo que permite una reconstitución horizontal\(s=6`` 14` 24 r=2`` 36\): a la\(6`\) que te queda\(2``30`\) unir,\(2``36`\) te da. 7
En las líneas Rev. 6-8, la calculadora introduce una tercera posición falsa: si\(R\) hubiera sido igual a 6, entonces\(r\) sería 5. La diferencia de 1 entre\(R\) y\(r\) es\(\frac{1}{5}\) de\(r\) o\(12^{\prime}\) veces\(r\). Ahora el verdadero valor de\(r\) es\(25^{\prime}\); para obtener\(R\) debemos de ahí “unirnos”\(12^{\prime} \cdot 25^{\prime}=5^{\prime}\) a él. Por lo tanto\(R=25^{\prime}+5^{\prime}=30^{\prime}=\frac{1}{2} \mathrm{NINDAN}\).
Uno podría creer que este tipo de problema es uno de los favoritos absolutos de los antiguos profesores babilónicos de matemáticas sofisticadas. Conocemos cuatro variantes de la misma que difieren en la elección de los parámetros numéricos. Sin embargo, todos pertenecen solo a dos tablillas que comparten una serie de particularidades terminológicas, por ejemplo, el uso del logograma\(\frac{1}{2}\) para la “fracción”, y el hábito de que los resultados se “dan”, no (por ejemplo) “vistos” o “subiendo”. Ambas tabletas son sin duda productos de la misma localidad y tradición local (según la ortografía basada en Uruk), y probablemente provienen de la misma escuela o incluso de la misma mano. Una variante más simple con un campo rectangular, sin embargo, se encuentra en un texto anterior de origen norteño, y también en un texto que pertenece junto a las variantes de trapecio; si no la favorita, la caña rota probablemente era una de las favoritas.