4.6: BM 13901 #23
- Page ID
- 109606
Rev. II
11 Alrededor de una superficie, las cuatro anchuras y la superficie que he amontonado,\(41^{\prime} 40^{\prime \prime}\).
12 4, los cuatro anchos, te inscribes. igi 4 es\(15^{\prime}\).
13\(15^{\prime}\) a\(41^{\prime} 40^{\prime \prime}\) que\(10^{\prime} 25^{\prime \prime}\) subas: te inscribes.
14 1, la proyección, te unes: por\(1^{\circ} 10^{\prime} 25^{\prime \prime}\),\(1^{\circ}5^{\prime}\) es igual.
15 1, la proyección, a la que te has unido, arrancas:\(5^{\prime}\) a dos
16 repites:\(10^{\prime}\),\(\mathrm{NINDAN}\), se enfrenta a sí mismo.
Mientras que el problema anterior ilustra el aspecto “moderno” de las matemáticas babilónicas antiguas, el presente parece ilustrar su lado arcaico, aunque provengan de la misma tablilla.
Esto no es una contradicción real. El problema actual #23 es intencionalmente arcaico. En otras palabras, es arcaico y no verdaderamente arcaico, lo que explica su aparición junto con los problemas “modernos” de una misma colección. El autor no es moderno y arcaico a la vez, muestra su virtuosismo jugando con arcaísmos. De varias maneras, las formulaciones que aquí se utilizan parecen imitar el lenguaje de los topógrafos acadios. El texto habla del ancho de un cuadrado, no de una “confrontación”; además, esta palabra aparece en la escritura silábica, lo cual es bastante excepcional (cf. nota 4, página 16). La frase introductoria “Sobre una superficie” 9 parece ser una versión abreviada de la fórmula característica que introduce un acertijo matemático: “si alguien te pregunta así sobre una superficie...” (cf. páginas 34, 110, 111 y 127). La expresión “los cuatro anchos” 10 refleja un interés por lo que realmente hay y por lo que llama la atención, un interés que caracteriza acertijos en general pero también los acertijos matemáticos que circularon entre los matemáticos practicantes del mundo premoderno (ver página 106). Incluso el método que se utiliza es típico de acertijos: el uso de un artificio asombroso que no invita a la generalización.
Así, el problema se puede expresar de la siguiente manera:
\(4 c+\square(c)=41^{\prime} 40^{\prime \prime}\).
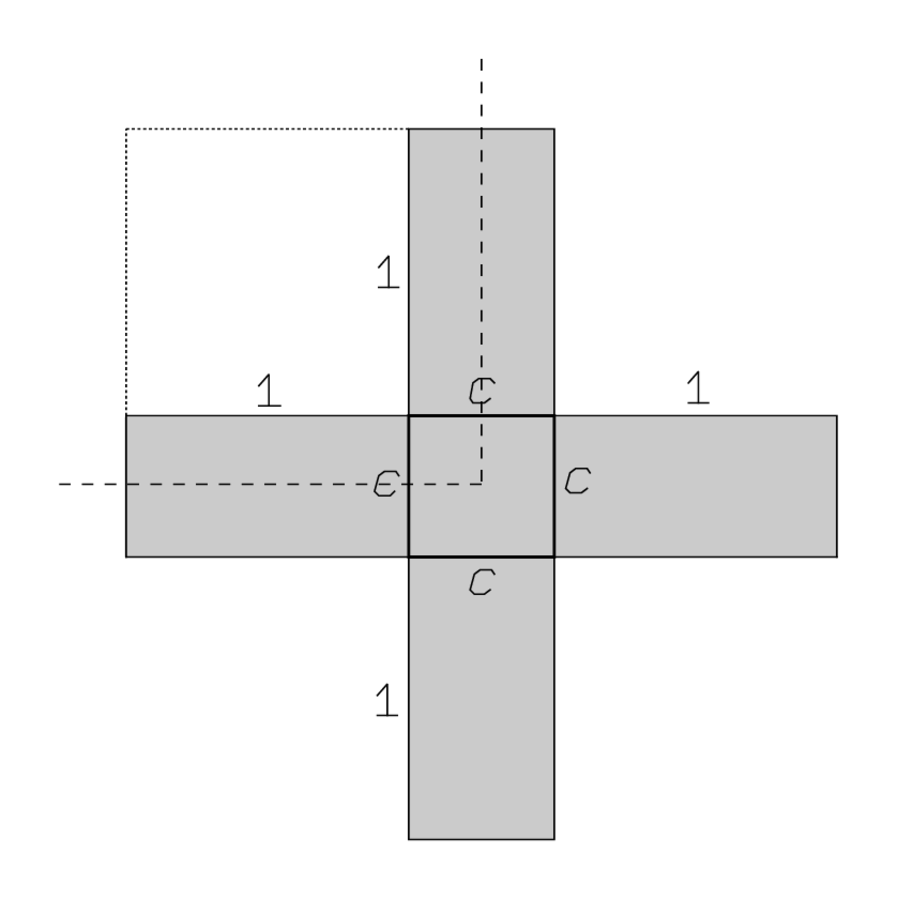
La Figura 4.12 deja claro el procedimiento: 4 c está representado por 4 rectángulos
\((1, c)\); el total corresponde\(41^{\prime} 40^{\prime \prime}\) así a la configuración en forma de cruz donde sobresale una “proyección” en cada una de las cuatro direcciones principales.
Las líneas 12—13 prescriben cortar\(\frac{1}{4}\) la cruz (demarcada por una línea punteada) y la “unión” de un complemento cuadrático\(\square(1)\) al gnomón que resulta. No hay necesidad de “aferrarse”, los lados del complemento ya están ahí en la posición correcta. Pero vale la pena notar que es la “proyección” misma la que se “une”: de ahí que no sea un mero número sino una configuración cuadrática identificada por su lado.
La terminación del gnomón da un cuadrado con área\(1^{\circ} 10^{\prime} 25^{\prime \prime}\) y por lo tanto lateral\(1^{\circ}5^{\prime}\). “Arrancando” la “proyección” —ahora como entidad unidimensional— nos encontramos\(5^{\prime}\). Duplicando el resultado, obtenemos el lado, que resulta ser\(10^{\prime}\). Aquí nuevamente, el texto evita el término habitual y no habla de un “enfrentamiento” como lo hacen los problemas “modernos” de la colección; en cambio dice que\(10^{\prime} \mathrm{NINDAN}\) “se enfrenta a sí mismo”.
Este método es tan diferente de cualquier otra cosa en el corpus total que Neugebauer creyó que era el resultado de la mezcla de un copista de dos problemas que pasa a tener sentido matemáticamente. Como veremos a continuación (página 109), la explicación es bastante diferente.
El aspecto arqueador, hay que añadir, no domina completamente. La línea 12, pidiendo primero la “inscripción” de 4 y señalando después su igi, parece describir el operativo en una tablilla para trabajos rudos que se impartieron en la escuela (ver nota 5, página 65, y página 120).