4.7: TMS VIII #1
- Page ID
- 109591
1 La superficie\(10^{\prime}\). El 4to del ancho al ancho me he unido, a 3 he ido... sobre
2 la longitud\(5^{\prime}\) fue más allá. Tú, 4, del cuarto, tanto como el ancho postular. El cuarto de 4 toma, 1 ya ves.
3 1 a 3 van, 3 ves. 4 cuartas partes del ancho a 3 se unen, 7 ves.
4 7 tanto como postulación de longitud. \(5^{\prime}\)el ir más allá a lo que va a ser arrancado de la posición de longitud. 7, de la longitud, a 4, ¿de la anchura? , elevar,
5 28 ves. 28, de las superficies, a\(10^{\prime}\) la superficie elevarse,\(4^{\circ}40^{\prime}\) ya ves.
6\(5^{\prime}\), el que va a ser arrancado de la longitud, a cuatro, del ancho, subir,\(20^{\prime}\) ya ves. \(\frac{1}{2}\)romper,\(10^{\prime}\) ya ves. \(10^{\prime}\)hacer bodega,
7\(1^{\prime} 40^{\prime \prime}\) ya ves. \(1^{\prime} 40^{\prime \prime}\)para\(4^{\circ}40^{\prime}\) unirse,\(4^{\circ} 41^{\prime} 40^{\prime \prime}\) ya ves. ¿Qué es igual? \(2^{\circ} 10^{\prime}\)ya ves.
8\(10^{\prime}\) ¿...? para\(2^{\circ} 10^{\prime}\) unirse,\(2^{\circ} 20^{\prime}\) ya ves. Qué al 28, de las superficies, ¿puedo postular cuál me\(2^{\circ} 10^{\prime}\) da?
9\(5^{\prime}\) postular. \(5^{\prime}\)a 7 subir,\(35^{\prime}\) ya ves. \(5^{\prime}\), el que va a ser arrancado de la longitud, de\(35^{\prime}\) arrancar,
10\(30^{\prime}\) ya ves,\(30^{\prime}\) la longitud. \(5^{\prime}\)la longitud a 4 del ancho subir,\(20^{\prime}\) ya ves, 20 el largo (error por ancho).
En BM 13901 #12 vimos cómo un problema sobre los cuadrados podría reducirse a un problema de rectángulo. Aquí, por el contrario, un problema sobre un rectángulo se reduce a un problema sobre cuadrados.
Traducido a símbolos, el problema es el siguiente;
\(\frac{7}{4} w-\ell=5^{\prime}\),
\((\ell, w)=10^{\prime}\)
(“a 3 he ido” en la línea 1 significa que la “unión” de\(\frac{1}{4} w\) en la línea 1 se repite tres veces). El problema podría haberse resuelto de acuerdo con los métodos utilizados en TMS IX #3 (página 57), es decir, de la siguiente manera:
\(7 w-4 \ell=4 \cdot 5^{\prime}\),\((\ell, w)=10^{\prime}\)
\(7 w-4 \ell=20^{\prime}\),\((7 w, 4 \ell)=(7 \cdot 4) \cdot 10^{\prime}=28 \cdot 10^{\prime}=4^{\circ} 40^{\prime}\)
\(7 w=\sqrt{4^{\circ} 40^{\prime}+\left(\frac{20^{\prime}}{2}\right)^{2}}+\frac{20^{\prime}}{2}=2^{\circ} 20\),
\ (\ begin {array} {l}
4\ ell=\ sqrt {4^ {\ circ} 40^ {\ prime} +\ left (\ frac {20^ {\ prime}} {2}\ derecha) ^ {2}} -\ frac {20^ {\ prime}} {2} =2\
w=20^ {\ prime},\ quad\ ell=30^ {prime}
\ end {array}\).
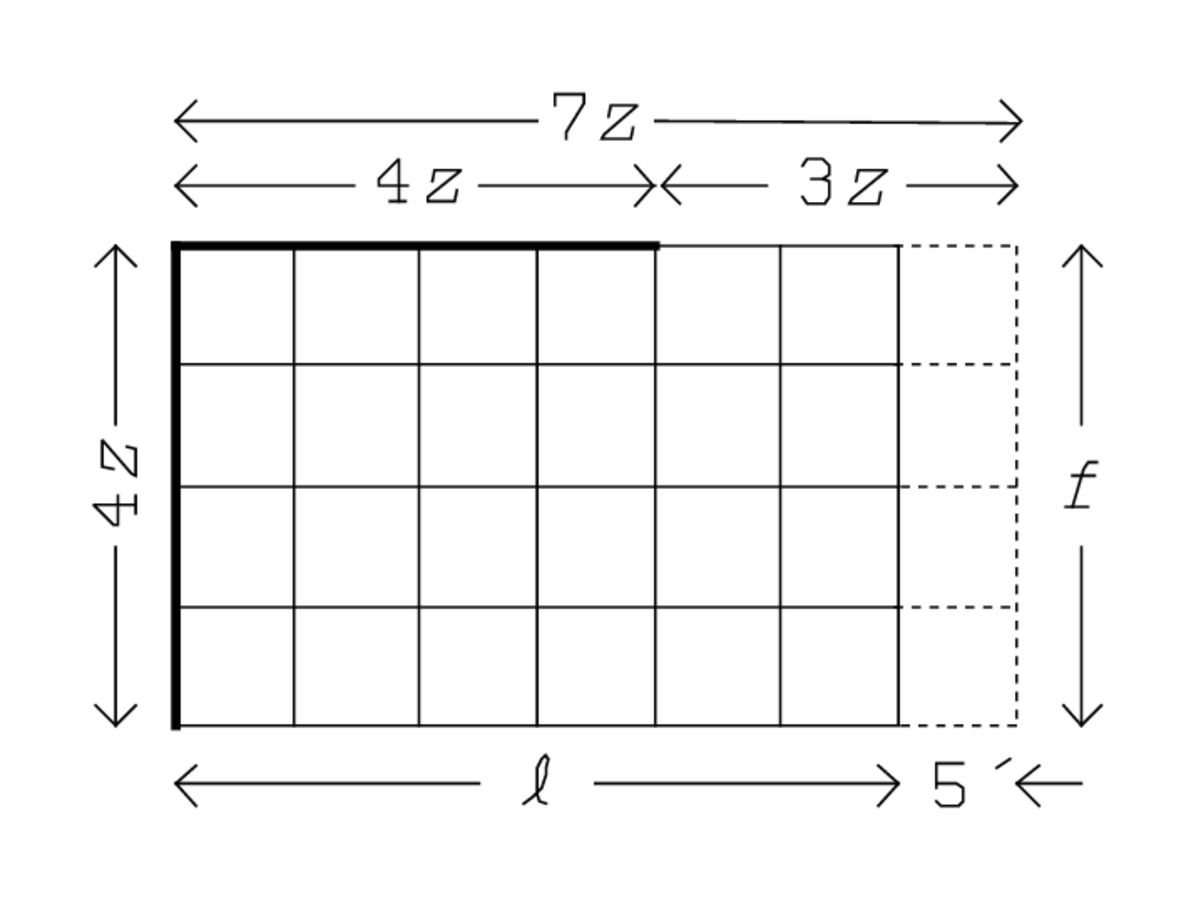
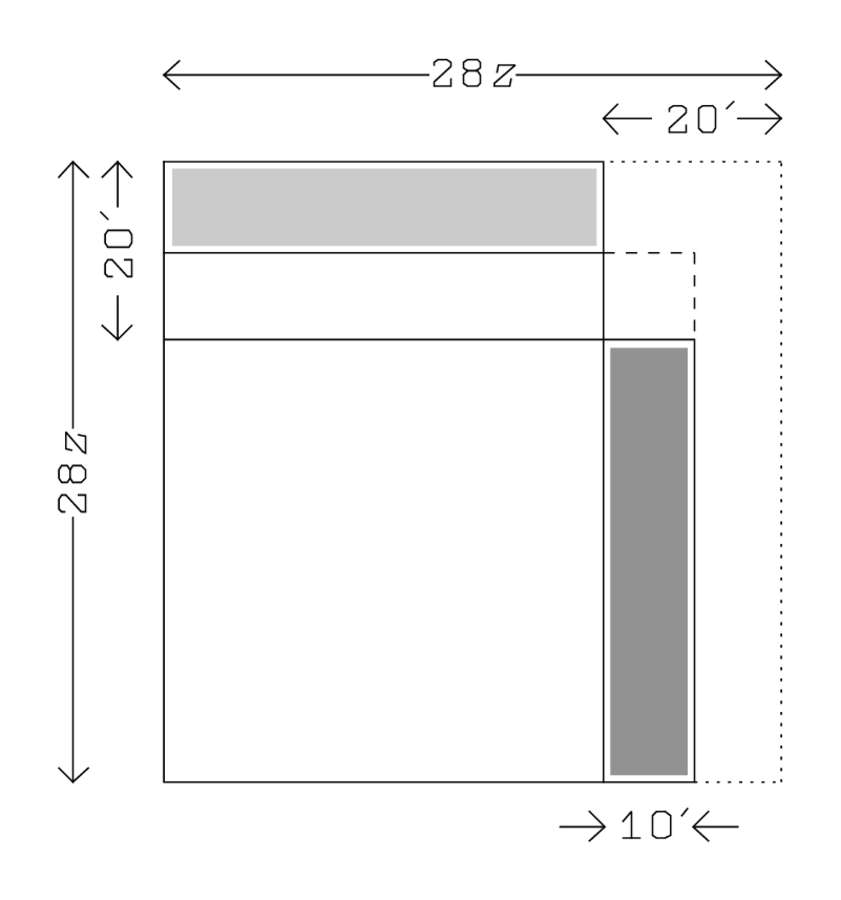
No obstante, una vez más la calculadora muestra que tiene varias cuerdas en su arco, y que puede elegir entre ellas como le parezca conveniente. Aquí construye su aproximación sobre un cuadrado cuyo lado\((z)\) es\(\frac{1}{4}\) del ancho (Figura 4.13). De esa manera, la anchura será igual a 4, entendida como 4\(z\) (Tú, 4, del cuarto, tanto como la anchura postular), y la longitud prolongada por\(5^{\prime}\) será igual a 7, entendida como\(7z\) (7 en la medida de lo posible). La línea 4 encuentra que el rectángulo con lados\(7z\) y\(4z\) —en otras palabras, el rectángulo inicial prolongado por\(5^{\prime}\) —consiste en\(7 \cdot 4=28\) pequeños cuadrados\(\square(z)\). 11 Estas 28 plazas rebasan el área\(10^{\prime}\) por cierto número de lados (\(n \cdot z\)), cuya determinación se aplaza hasta más tarde. Como de costumbre, de hecho, el problema no normalizado
\(28 \square(z)-n \cdot z=10^{\prime}\)
se transforma en
\(\square(28 z)-n \cdot(28 z)=28 \cdot 10^{\prime}=4^{\circ} 40^{\prime}\).
La línea 6 encuentra\(n=4 \cdot 5^{\prime}=20^{\prime}\), y de aquí en adelante todo sigue la rutina, como puede verse en la Figura 4.14: 28\(z\) será igual a\(2^{\circ} 20\), y\(z\) por lo tanto a\(5^{\prime}\). 12 Por lo tanto, la longitud\(\ell\) será\(7 \cdot 5^{\prime}-5^{\prime}=30^{\prime}\), y la anchura\(w\)\(4 \cdot 5^{\prime}=20^{\prime}\).
