4.8: YBC 6504 #4

Última actualización
Guardar como PDF

Page ID: 109548

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Rev.

11 Tanto como el largo sobre el ancho va más allá, hecho encuentro, desde el interior de la superficie he arrancado:

12\(8^{\prime} 20^{\prime \prime}\). \(20^{\prime}\)el ancho, su largo ¿qué?

13 encuentro\(20^{\prime}\) hecho:\(6^{\prime} 40^{\prime \prime}\) postula.

14\(6^{\prime} 40^{\prime \prime}\) a\(8^{\prime} 20^{\prime \prime}\) que te unes:\(15^{\prime}\) postulas.

15 Por\(15^{\prime}\),\(30^{\prime}\) es igual. \(30^{\prime}\), la longitud, usted postula.

Hasta el momento, todo lo que hemos mirado era matemáticamente correcto, aparte de algunos errores de cálculo y copia. Pero todos los que practican matemáticas a veces también cometen errores en el argumento; no es de extrañar entonces que los babilonios a veces lo hicieran.

El presente texto ofrece un ejemplo. Traducido a símbolos, el problema es el siguiente:

alt \((\ell, w)-\square(\ell-w)=8^{\prime} 20^{\prime \prime} \quad, \quad w=20^{\prime}\).

Sorprendentemente, la longitud se encuentra como aquella que “es igual por”
alt \((\ell, w)-\square(\ell-w)+\square(w)\) —es decir, después de una transformación y expresada en símbolos, como\(\sqrt{(3 w-\ell) \cdot \ell}\).

Figura\(4.15\): Las operaciones de cortar y pegar de YBC 6504 #4.

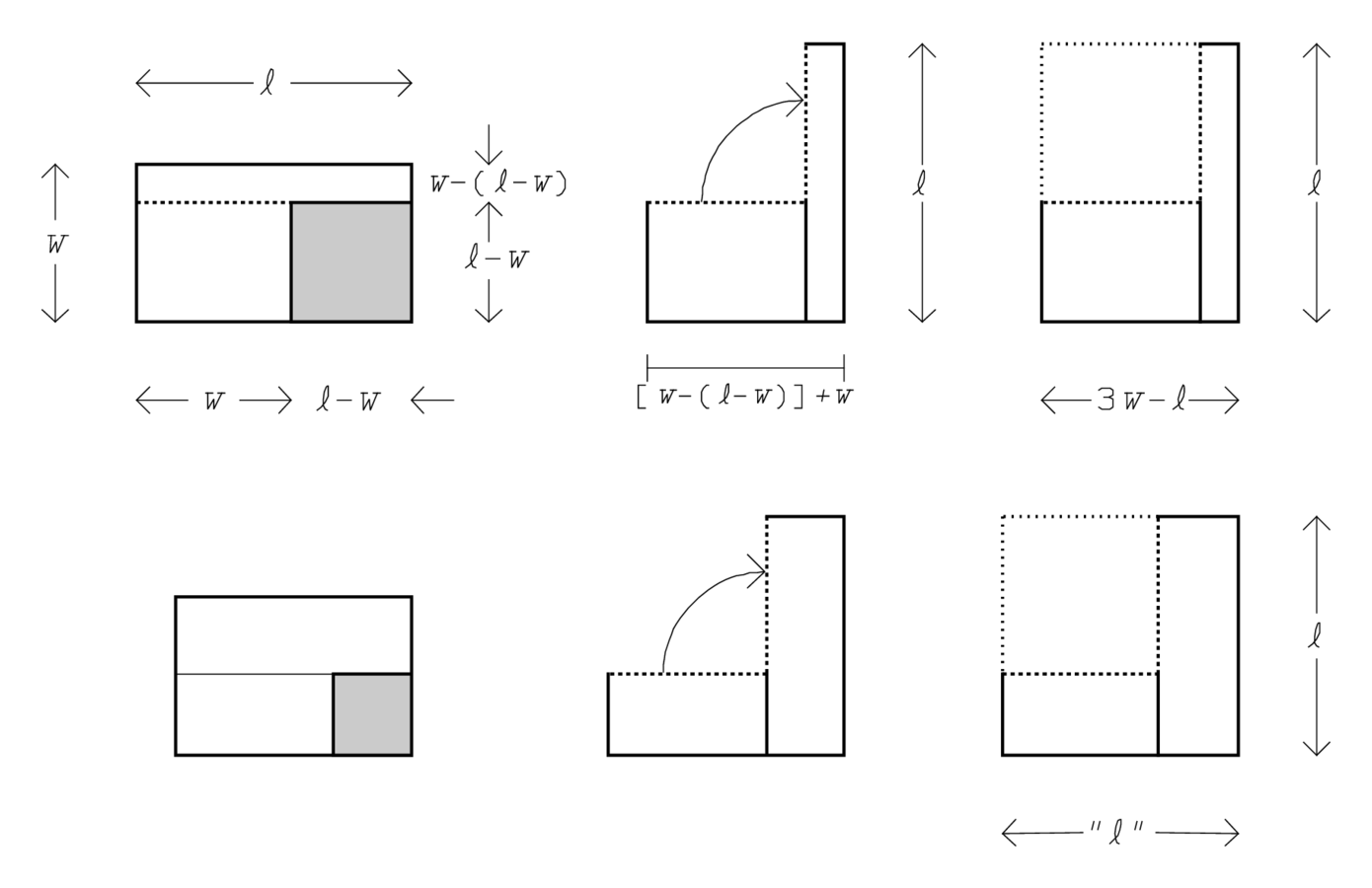
El error parece difícil de explicar, pero la inspección de la geometría del argumento revela su origen (Figura 4.15). Encima el procedimiento se presenta en proporciones distorsionadas; vemos que la “unión” de\(\square(w)\) presupone que el rectángulo mutilado se corte a lo largo de la línea punteada y se abra como un pseudo-gnomón. Es claro que lo que resulta de la finalización de esta configuración no es\(\square(\ell)\) sino en su lugar —si se cuenta bien— alt \((3 w-\ell, \ell)\). A continuación vemos lo mismo, pero ahora en las proporciones del problema real, y ahora el error ya no es evidente. Aquí,\(\ell = 30^{\prime}\) y\(2 = 20^{\prime}\), y por lo tanto\(\ell-w=w-(\ell-w)\). En consecuencia el rectángulo mutilado se abre como un verdadero gnomón, y la cifra completada corresponde a\ square (t) —pero sólo porque\(\ell=\frac{3}{2} w\).

Este error ilustra un aspecto importante de la geometría “ingenua”: como suele ser el caso de las demostraciones geométricas, se debe prestar una atención escrupulosa para que no se induzca al error por lo que se ve “inmediatamente”. La rareza de tales errores es evidencia de la alta competencia de la Antigua Babilonia calculadoras y muestra que casi siempre fueron capaces de distinguir las magnitudes dadas de un problema de lo que más sabían al respecto.