2.3: Los números de Fibonacci en un girasol

Considere la foto de un girasol que se muestra en la Fig. 2.1, y observe las espirales aparentes en los floretes que irradian desde el centro hasta el borde. Estas espirales parecen girar tanto en sentido horario como antihorario. Al contarlos, se encuentran 34 espirales en sentido horario y 21 espirales en sentido antihorario. Los números 21 y 34 son notables ya que son números consecutivos en la secuencia de Fibonacci.

¿Por qué aparecen los números de Fibonacci en la cabeza de girasol? Para responder a esta pregunta, construimos un modelo muy simple para la forma en que se desarrollan los floretes. Supongamos que durante el desarrollo, primero aparecen floretes cerca del centro de la cabeza y posteriormente se mueven radialmente hacia afuera con velocidad constante a medida que crece la cabeza de girasol. Para llenar la cabeza circular de girasol, suponemos que a medida que cada nuevo florete se crea en el centro, se gira en un ángulo constante antes de moverse radialmente. Asumiremos además que el ángulo de rotación es óptimo en el sentido de que la cabeza de girasol resultante consiste en floretes que están bien espaciados.

Figura 2.1: La cabeza en flor de un girasol.

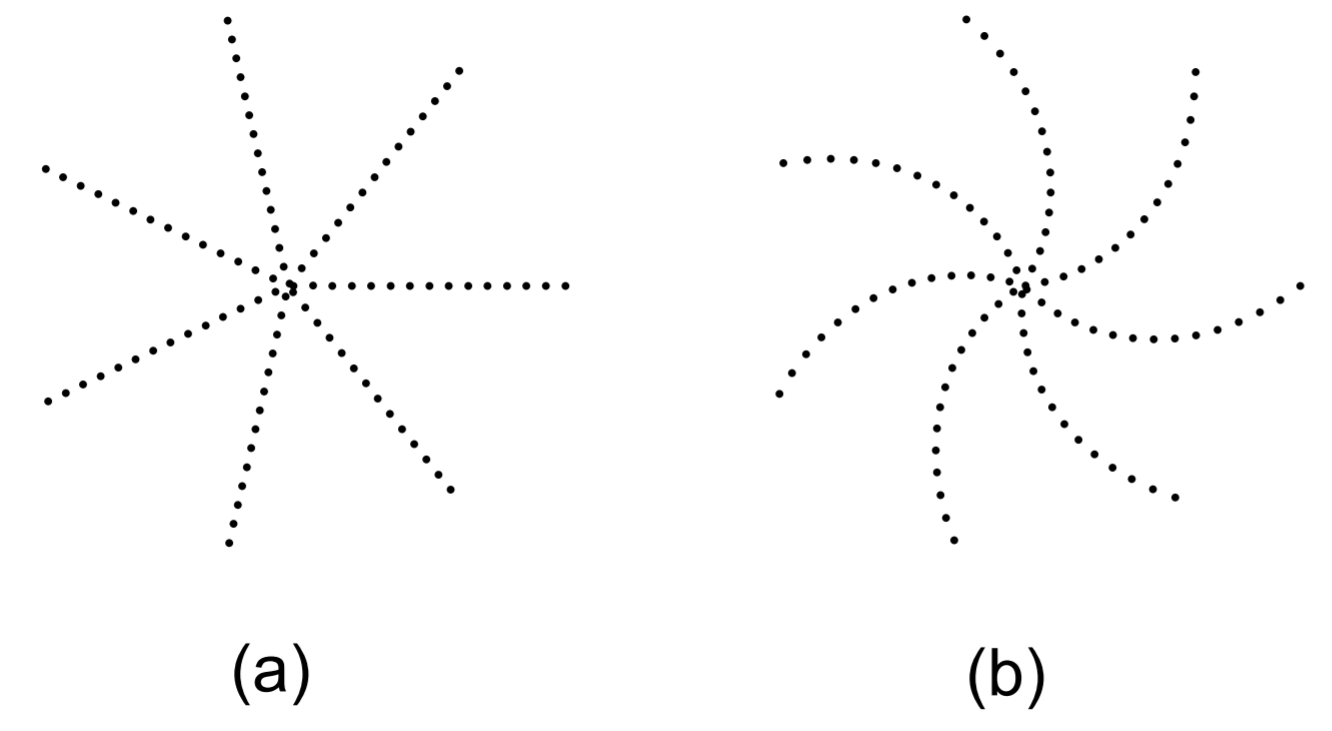
Denotemos el ángulo de rotación por\(2 \pi \alpha\). Primero consideramos la posibilidad de que\(\alpha\) sea un número racional, digamos\(n / m\), donde\(n\) y\(m\) sean enteros positivos sin factores comunes, y\(n<m\). Dado que después de\(m\) las rotaciones los floretes volverán a la línea radial sobre la que comenzaron, la cabeza de girasol resultante consiste en floretes tendidos a lo largo de líneas\(m\) rectas. Tal cabeza de girasol para\(\alpha=1 / 7\) se muestra en la Fig. \(2.2 \mathrm{a}\), donde se observan siete líneas rectas. Evidentemente, los valores racionales para\(\alpha\) no dan como resultado floretes bien espaciados. Esta figura y las posteriores se produjeron utilizando MATLAB, y el código de simulación se muestra al final de esta subsección.

¿Qué pasa con los valores irracionales? No importa cuántas rotaciones, los floretes nunca volverán a su línea radial inicial. Sin embargo, la cabeza de girasol resultante puede no tener floretes bien espaciados. Por ejemplo, si\(\alpha=\pi-3\), entonces la cabeza de girasol resultante se parece a la Fig. 2.2b. Ahí, se pueden ver siete espirales en sentido contrario a las agujas del reloj. Recordemos que una buena aproximación racional a\(\pi\) es\(22 / 7\), que es ligeramente mayor que\(\pi\). En cada séptima rotación en sentido antihorario, entonces, el nuevo florete cae justo por debajo de la línea radial seguida por el florete de hace siete rotaciones.

Los números irracionales que tienen más probabilidades de construir una cabeza de girasol con floretes bien espaciados son aquellos que no pueden aproximarse bien por números racionales. Aquí, elegimos el llamado ángulo dorado, tomando\(\alpha=1-\phi\), de modo que\(2 \pi(1-\phi) \approx 137.5^{\circ}\), y realizamos rotaciones en sentido horario. Las aproximaciones racionales a\(1-\phi\) están dadas por\(F_{n} / F_{n+2}\), de manera que el número de espirales observadas corresponderá a los números de Fibonacci.

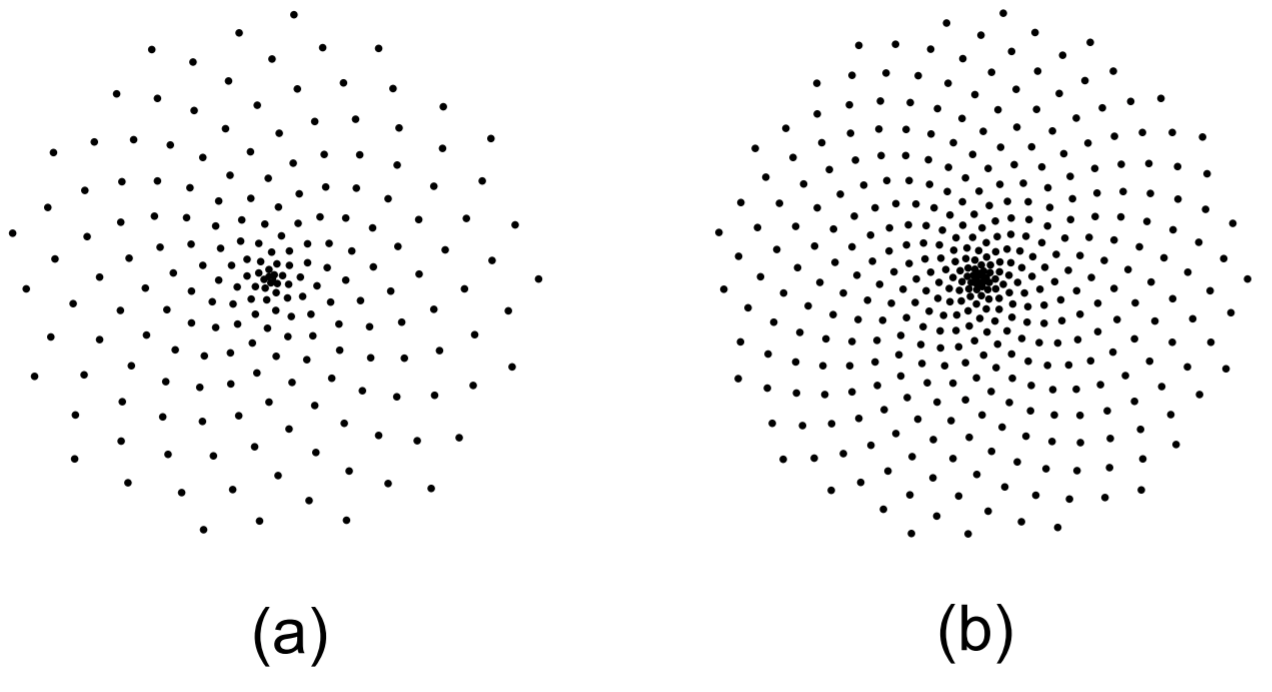
Dos simulaciones de la cabeza de girasol con\(\alpha=1-\phi\) se muestran en la Fig. \(2.3\). Estas simulaciones difieren solo por la elección de la velocidad radial. En la Fig. \(2.3 \mathrm{a}\), se pueden contar 13 espirales en sentido horario y 21 espirales en sentido contrario a las agujas del reloj; en la Fig. \(2.3 \mathrm{~b}\), hay 21 espirales en sentido antihorario y 34 espirales en sentido horario, al igual que la cabeza de girasol que se muestra en la Fig. 2.1.

Figura 2.2: Simulación de una cabeza de girasol para (a)\(\alpha=1 / 7 ;\) (b)\(\alpha=\pi-3 .\)

Figura 2.3: Simulación de una cabeza de girasol para\(\alpha=1-\phi\). a)\(v 0=1 / 2\); b)\(v 0=1 / 4\).