4.3: El modelo de enfermedad epidémica SIR
- Page ID
- 117596
El modelo SIR, publicado por primera vez por Kermack y McKendrick en 1927, es sin duda el modelo matemático más famoso para la propagación de una enfermedad infecciosa. Aquí, las personas se caracterizan en tres clases: susceptibles\(S\), infecciosas\(I\) y removidas R. Los individuos retirados ya no son susceptibles ni infecciosos por cualquier motivo; por ejemplo, se han recuperado de la enfermedad y ahora son inmunes, o han sido vacunados, o han sido aislados del resto de la población, o quizá hayan muerto a causa de la enfermedad. Al igual que en el modelo SIS, asumimos que los infecciosos abandonan la\(I\) clase con tasa constante\(\gamma\), pero en el modelo SIR se mueven directamente a la\(R\) clase. El modelo puede ser esquematizado como
\[S \stackrel{\beta S I}{\longrightarrow} I \stackrel{\gamma I}{\longrightarrow} R, \nonumber \]
y las ecuaciones diferenciales acopladas correspondientes son
\[\frac{d S}{d t}=-\beta S I, \quad \frac{d I}{d t}=\beta S I-\gamma I, \quad \frac{d R}{d t}=\gamma I, \nonumber \]
con la constante restricción poblacional\(S+I+R=N\). Por conveniencia, no dimensionalizamos (4.3.2) usando\(N\) para el tamaño de la población y\(\gamma^{-1}\) para el tiempo; es decir, vamos
\[\hat{S}=S / N, \quad \hat{I}=I / N, \quad \hat{R}=R / N, \quad \hat{t}=\gamma t \nonumber \]
y definir la relación reproductiva básica adimensional como
\[\mathcal{R}_{0}=\frac{\beta N}{\gamma} \nonumber \]
Las ecuaciones SIR adimensionales son dadas por
\[\frac{d \hat{S}}{d \hat{t}}=-\mathcal{R}_{0} \hat{S} \hat{I}, \quad \frac{d \hat{I}}{d \hat{t}}=\mathcal{R}_{0} \hat{S} \hat{I}-\hat{I}, \quad \frac{d \hat{R}}{d \hat{t}}=\hat{I}, \nonumber \]
con restricción adimensional\(\hat{S}+\hat{I}+\hat{R}=1\).
Utilizaremos el modelo SIR para abordar dos preguntas fundamentales: (1) ¿Bajo qué condiciones ocurre una epidemia? (2) Si ocurre una epidemia, ¿qué fracción de una población bien mezclada se enferma?
\(\left(\hat{S}_{*}, \hat{I}_{*}, \hat{R}_{*}\right)\)Dejen ser los puntos fijos de (4.3.5). Estableciendo\(d \hat{S} / d \hat{t}=d \hat{I} / d \hat{t}=d \hat{R} / d \hat{t}=0\), inmediatamente observamos a partir de la ecuación para\(d \hat{R} / d \hat{t}\) eso\(\hat{I}=0\), y este valor obliga a todos los derivados del tiempo a desvanecerse para cualquier\(\hat{S}\) y\(\hat{R}\). Ya que con\(\hat{I}=0\), tenemos\(\hat{R}=1-\hat{S}\), evidentemente todos los puntos fijos de (4.3.5) están dados por la familia de un parámetro\(\left(\hat{S}_{*}, \hat{I}_{*}, \hat{R}_{*}\right)=\left(\hat{S}_{*}, 0,1-\hat{S}_{*}\right) .\)
Una epidemia ocurre cuando un pequeño número de infecciosos introducidos en una población susceptible da como resultado un número creciente de infecciosos. Podemos asumir una población inicial en un punto fijo de\((4.3.5)\), perturbar este punto fijo introduciendo un pequeño número de infecciosos y determinar la estabilidad del punto fijo. Una epidemia ocurre cuando el punto fijo es inestable. El problema de estabilidad lineal puede resolverse considerando únicamente la ecuación para\(d \hat{I} / d \hat{t}\) in (4.3.5). Con\(\hat{I} \ll 1\) y\(\hat{S} \approx \hat{S}_{0}\), tenemos
\[\frac{d \hat{I}}{d \hat{t}}=\left(\mathcal{R}_{0} \hat{S}_{0}-1\right) \hat{I} \nonumber \]
para que ocurra una epidemia si\(\mathcal{R}_{0} \hat{S}_{0}-1>0\). Con la relación reproductiva básica dada por (4.3.4), y\(S_{0}=S_{0} / N\), donde\(S_{0}\) está el número de individuos susceptibles iniciales, se produce una epidemia si
\[\mathcal{R}_{0} \hat{S}_{0}=\frac{\beta S_{0}}{\gamma}>1 \nonumber \]
lo que podría haberse adivinado. Una epidemia ocurre si un individuo infeccioso introducido en una población de individuos\(S_{0}\) susceptibles infecta en promedio a más de otra persona. Si ocurre una epidemia, entonces inicialmente el número de individuos infecciosos aumenta exponencialmente con la tasa de crecimiento\(\beta S_{0}-\gamma\).
que tras la integración y simplificación, da como resultado la siguiente ecuación trascendental para\(\hat{R}_{\infty}\):
\[1-\hat{R}_{\infty}-e^{-\mathcal{R}_{0} \hat{R}_{\infty}}=0, \nonumber \]
una ecuación que se puede resolver numéricamente usando el método de Newton. Tenemos
\[\begin{aligned} &F\left(\hat{R}_{\infty}\right)=1-\hat{R}_{\infty}-e^{-\mathcal{R}_{0} \hat{R}_{\infty}} \\[4pt] &F^{\prime}\left(\hat{R}_{\infty}\right)=-1+\mathcal{R}_{0} e^{-\mathcal{R}_{0} \hat{R}_{\infty}} \end{aligned} \nonumber \]
y el método de Newton para resolver\(F\left(\hat{R}_{\infty}\right)=0\) iteraciones
\[\hat{R}_{\infty}^{(n+1)}=\hat{R}_{\infty}^{n}-\frac{F\left(\hat{R}_{\infty}^{(n)}\right)}{F^{\prime}\left(\hat{R}_{\infty}^{(n)}\right)} \nonumber \]
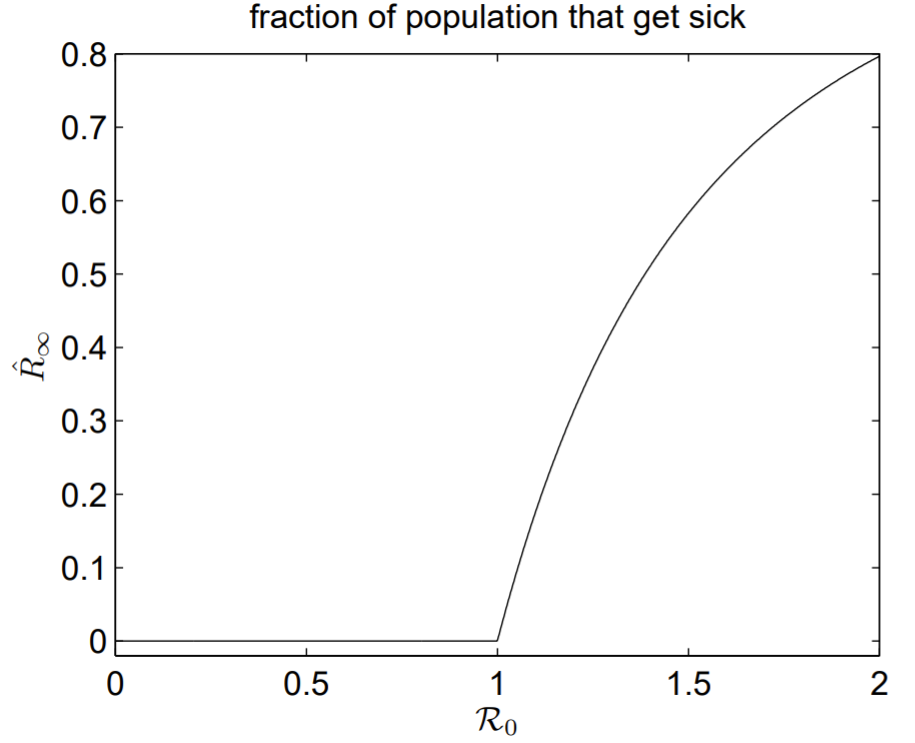
para fijo\(\mathcal{R}_{0}\) y una condición inicial adecuada para\(R_{\infty}^{(0)}\), que tomamos como unidad. Mi código para la computación\(R_{\infty}\) en función de\(\mathcal{R}_{0}\) se da a continuación, y el resultado se muestra en la Fig. 4.1. Hay una explosión en el número de infecciones a medida que\(\mathcal{R}_{0}\) aumenta desde la unidad, y este rápido incremento es un ejemplo clásico de lo que se conoce más generalmente como un fenómeno umbral.




