5.4: Equilibrio de Vinculación
- Page ID
- 117621
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al considerar un polimorfismo en un solo locus genético, asumimos dos alelos distintos,\(A\) y\(a\). El diploide se presenta entonces como uno de tres tipos:\(A A, A a\) y aa. Consideramos ahora un polimorfismo en dos loci genéticos, cada uno con dos alelos distintos. Si los alelos en los primeros loci genéticos son\(A\) y\(a\), y aquellos en el segundo\(B\) y\(b\), entonces son posibles cuatro gametos haploides distintos, a saber\(A B, A b, a B\) y\(a b\). Diez diplotipos distintos son posibles, obtenidos formando pares de todos los haplotipos posibles. Podemos escribir estos diez diplotipos como\(A B / A B, A B / A b, A B / a B, A B / a b\),\(A b / A b, A b / a B, A b / a b, a B / a B, a B / a b\), y\(a b / a b\), donde el numerador representa el haplotipo de un padre, el denominador representa el haplotipo del otro padre. No distinguimos aquí qué haplotipo vino de qué progenitor.
Para continuar, definimos las frecuencias alélicas y gaméticas para nuestro problema de dos loci en la Tabla 5.13. Si la probabilidad de que un gameto contenga alelo\(A\) o\(a\) no depende de si el gameto contiene alelo\(B\) o\(b\), entonces se dice que los dos loci son independientes. Bajo el supuesto de independencia, las frecuencias gaméticas son los productos de las frecuencias alélicas, es decir\(p_{A B}=p_{A} p_{B}, p_{A b}=p_{A} p_{b}\), etc.
A menudo, los dos loci no son independientes. Esto puede deberse a la selección epistática, o epistasis. Como ejemplo, supongamos que dos loci en humanos influyen en la altura, y que el genotipo más apto es el que resulta en una estatura promedio. La selección que favorece el valor poblacional promedio de un rasgo se denomina normalización o estabilización. Supongamos que\(A\) y\(B\) son alelos altos hipotéticos,\(a\) y\(b\) son alelos cortos, y una persona con dos alelos altos y dos cortos obtiene estatura promedio. Entonces la selección puede favorecer los genotipos específicos\(A B / a b, A b / A b, A b / a B\), y\(a B / a B\). La selección puede actuar contra ambos genotipos que producen alturas superiores a la media,\(A B / A B, A B / A b\), y\(A B / a B\), y aquellos que producen alturas por debajo del promedio,\(A b / a b, a B / a b\) y\(a b / a b\). La selección epistática ocurre porque la aptitud de los\(A, a\) loci depende de qué alelos estén presentes en los\(B, b\) loci. Aquí,\(A\) tiene mayor estado físico cuando se combina con\(b\) que cuando se empareja con\(B\).
Los dos loci también pueden no ser independientes debido a un tamaño de población finito (es decir, efectos estocásticos). Por ejemplo, supongamos que una mutación\(a \rightarrow A\) ocurre solo una vez en una población finita (en una población infinita, cualquier posible mutación ocurre un número infinito de veces), y eso\(A\) es fuertemente favorecido por la selección natural. La frecuencia de\(A\) puede entonces aumentar. Si un locus polimórfico cercano en el mismo cromosoma\(A\) que pasa a ser\(B\) (digamos, con un polimorfismo\(b\) en la población), entonces los\(A B\) gametos pueden aumentar sustancialmente en frecuencia, con\(A b\) ausentes. Decimos que el alelo\(B\) autoestopistas con el alelo favorecido\(A\).
Cuando los dos loci no son independientes, decimos que los loci están en desequilibrio de fase gamética, o más comúnmente desequilibrio de ligamiento, a veces abreviado como LD. Cuando los loci son independientes, decimos que están en equilibrio de vinculación. Aquí, modelaremos cómo dos loci, inicialmente en desequilibrio de ligamiento, abordan el equilibrio de ligamiento a través del proceso de recombinación.
Para comenzar, necesitamos una comprensión rudimentaria de la meiosis. Durante la meiosis,
| genotipo de alelo o gameto | \(A\) | \(a\) | \(B\) | \(b\) | \(A B\) | \(A b\) | \(a B\) | \(a b\) |
|---|---|---|---|---|---|---|---|---|
| frecuencia | \(p_{A}\) | \(p_{a}\) | \(p_{B}\) | \(p_{b}\) | \(p_{A B}\) | \(p_{A b}\) | \(p_{a B}\) | \(p_{a b}\) |
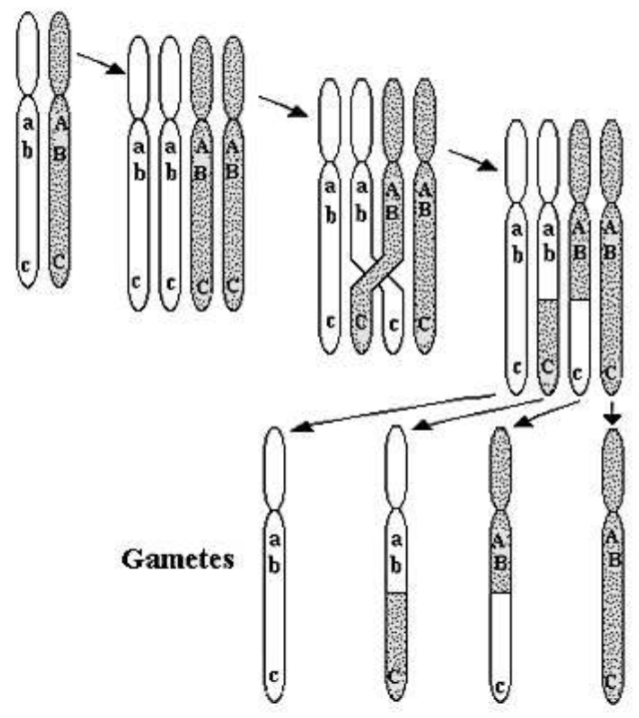
El ADN de la célula diploide, dispuesto en moléculas muy largas llamadas cromosomas, se replica una vez y se separa dos veces, produciendo cuatro células haploides, cada una conteniendo la mitad de los cromosomas de la célula original. La reproducción sexual da como resultado la singamia, la fusión de un óvulo haploide y un espermatozoide para formar una célula cigoto diploide.
Fig. \(5.2\)presenta un esquema de meiosis y el proceso de cruzamiento que resulta en recombinación. En un diploide, cada cromosoma tiene un cromosoma hermano correspondiente, un cromosoma originario del óvulo, uno del esperma. Estos cromosomas hermanos tienen los mismos genes, pero posiblemente diferentes alelos. En la Fig. 5.2, se muestran esquemáticamente los alelos\(a, b, c\) en el cromosoma claro y los alelos\(A, B, C\) en el cromosoma oscuro de su hermana. En el primer paso de la meiosis, cada cromosoma se replica exactamente. En el segundo paso, los cromosomas hermanos intercambian material genético por el proceso de cruce. Luego, los cuatro cromosomas se separan en células haploides. Observe desde el esquema que el proceso de cruce puede resultar en recombinación genética. Supongamos que el esquema de la Fig. \(5.2\)representa la producción de esperma por un macho. Si el cromosoma del padre del varón contiene los alelos\(A B C\) y el de la madre del varón\(a b c\), la recombinación puede dar como resultado que el esperma contenga un cromosoma con alelos\(A B c\) (el tercer gameto en la Fig. 5.2). Decimos que este cromosoma es un recombinante; contiene alelos tanto de su abuelo paterno como de su abuela paterna. Es probable que la combinación precisa de alelos en este cromosoma recombinante nunca haya existido antes en una sola persona. La recombinación es la razón por la que todos, a excepción de los gemelos idénticos, son genéticamente únicos.
Se dice que los genes que se presentan en el mismo cromosoma están vinculados. Cuanto más cerca estén los genes entre sí en el cromosoma, más estrecho será el enlace, y menos probable es que la recombinación los separe. Es probable que los genes estrechamente vinculados se hereden del mismo abuelo. Por definición, los genes en diferentes cromosomas están desvinculados; la variedad independiente de cromosomas da como resultado la\(50 \%\) posibilidad de que un gameto reciba los genes de cualquiera de los abuelos. Para definir y modelar la evolución del desequilibrio de ligamiento, primero obtenemos frecuencias alélicas a partir de frecuencias gaméticas mediante
\[\begin{array}{ll} p_{A}=p_{A B}+p_{A b}, & p_{a}=p_{a B}+p_{a b} \\[4pt] p_{B}=p_{A B}+p_{a B}, & p_{b}=p_{A b}+p_{a b} \end{array} \nonumber \]
Dado que las frecuencias suman a la unidad,
\[p_{A}+p_{a}=1, \quad p_{B}+p_{b}=1, \quad p_{A B}+p_{A b}+p_{a B}+p_{a b}=1 . \nonumber \]
Existen tres frecuencias gameticas independientes y solo dos frecuencias alélicas independientes, por lo que en general no es posible obtener las frecuencias gameticas a partir de las frecuencias alélicas sin asumir una restricción adicional como el equilibrio de ligamiento. Podemos, sin embargo, introducir una variable adicional\(D\), llamada el coeficiente de desequilibrio de ligamiento, y\(D\) definir como la diferencia entre la frecuencia gametica\(p_{A B}\) y lo que sería esta frecuencia gametica si los loci estuvieran en ligamiento equilibrio:
\[p_{A B}=p_{A} p_{B}+D \nonumber \]
Usando\(p_{A B}+p_{A b}=p_{A}\) para eliminar\(p_{A B}\) en (5.4.3), obtenemos
\[p_{A b}=p_{A} p_{b}-D \nonumber \]
Del mismo modo, utilizando\(p_{A B}+p_{a B}=p_{B}\)
\[p_{a B}=p_{a} p_{B}-D \nonumber \]
y usando\(p_{a b}+p_{a b}=p_{a}\)
\[p_{a b}=p_{a} p_{b}+D . \nonumber \]
Con nuestra definición, el desequilibrio de ligamiento positivo\((D>0)\) implica excesivo\(A B\) y\(a b\) gametos y deficientes\(A b\) y\(a B\) gametos; desequilibrio de ligamiento negativo\((D<0)\) implica lo contrario. \(D\)alcanza su valor máximo de\(1 / 4\) cuándo\(p_{A B}=\)\(p_{a b}=1 / 2\), y alcanza su valor mínimo de\(-1 / 4\) cuándo\(p_{A b}=p_{a B}=1 / 2\). Una igualdad obtenible de (5.4.3, 5.4.4, 5.4.5, 5.4.6) que más adelante encontraremos útil es
\[\begin{align} \nonumber p_{A B} p_{a b}-p_{A b} p_{a B} &=\left(p_{A} p_{B}+D\right)\left(p_{a} p_{b}+D\right)-\left(p_{A} p_{b}-D\right)\left(p_{a} p_{B}-D\right) \\[4pt] \nonumber &=D\left(p_{A} p_{B}+p_{a} p_{b}+p_{A} p_{b}+p_{a} p_{B}\right) \\[4pt] &=D \end{align} \nonumber \]
Sin selección y mutación,\(D\) evoluciona solo por recombinación. Con primos que representan los valores de la próxima generación, y utilizando\(p_{A}^{\prime}=p_{A}\) y\(p_{B}^{\prime}=p_{B}\) debido a que la reproducción sexual por sí misma no cambia las frecuencias alélicas,
\[\begin{aligned} D^{\prime} &=p_{A B}^{\prime}-p_{A}^{\prime} p_{B}^{\prime} \\[4pt] &=p_{A B}^{\prime}-p_{A} p_{B} \\[4pt] &=p_{A B}^{\prime}-\left(p_{A B}-D\right) \\[4pt] &=D+\left(p_{A B}^{\prime}-p_{A B}\right), \end{aligned} \nonumber \]
donde hemos utilizado (5.4.3) para obtener la tercera igualdad. Por lo tanto, el cambio en\(D\) es igual al cambio en la frecuencia de los\(A B\) gametos,
\[D^{\prime}-D=p_{A B}^{\prime}-p_{A B} \nonumber \]
| freq gameto/ freq diploide | |||||
| diploide | frecuencia de inmersión | AB | Ab | aB | ab |
| \(A B / A B\) | \(p_{A B}^{2}\) | 1 | 0 | 0 | 0 |
| \(A B / A b\) | \(2 p_{A B} p_{A b}\) | \(1 / 2\) | \(1 / 2\) | 0 | 0 |
| \(A B / a B\) | \(2 p_{A B} p_{a B}\) | \(1 / 2\) | 0 | \(1 / 2\) | 0 |
| \(A B / a b\) | \(2 p_{A B} p_{a b}\) | \((1-r) / 2\) | \(r / 2\) | \(r / 2\) | \((1-r) / 2\) |
| \(A b / A b\) | \(p_{A b}^{2}\) | 0 | 1 | 0 | 0 |
| \(A b / a B\) | \(2 p_{A b} p_{a B}\) | \(r / 2\) | \((1-r) / 2\) | \((1-r) / 2\) | \(r / 2\) |
| \(A b / a b\) | \(2 p_{A b} p_{a b}\) | 0 | \(1 / 2\) | 0 | \(1 / 2\) |
| \(a B / a B\) | \(p_{a B}^{2}\) | 0 | 0 | 1 | 0 |
| \(a B / a b\) | \(2 p_{a B} p_{a b}\) | 0 | 0 | \(1 / 2\) | \(1 / 2\) |
| \(a b / a b\) | \(p_{a b}^{2}\) | 0 | 0 | 0 | 1 |
Para entender por qué las frecuencias gaméticas cambian a través de las generaciones, primero debemos reconocer cuándo no cambian. Sin recombinación genética, los cromosomas mantienen su identidad exacta a través de generaciones. Por lo tanto, las frecuencias cromosómicas sin recombinación son constantes, y para los loci genéticos en el mismo cromosoma con alelos\(\mathrm{A}, \mathrm{a}\) y\(\mathrm{B}, \mathrm{b}\), digamos,\(p_{A B}^{\prime}=p_{A B} .\) en una población infinita sin selección ni mutación, las frecuencias gaméticas cambian solo para los loci genéticos en desequilibrio de ligamiento en diferentes cromosomas, o para loci genéticos en desequilibrio de ligamiento en el mismo cromosoma sometido a recombinación genética.
Calcularemos la frecuencia\(p_{A B}^{\prime}\) de los\(A B\) gametos en la próxima generación, dada la frecuencia\(p_{A B}\) de los\(A B\) gametos en la generación actual, utilizando dos métodos diferentes. El primer método utiliza una mesa de acoplamiento. El segundo método hace un argumento de probabilidad directa.
La tabla de acoplamiento se muestra en la Tabla 5.14. La primera columna es el diplotipo parental antes de la meiosis. La segunda columna es la frecuencia de diplotipos asumiendo apareamiento aleatorio. Las siguientes cuatro columnas son las frecuencias del genotipo haploide (normalizadas por las frecuencias diploides correspondientes para simplificar la presentación de la tabla). Aquí, definimos como la frecuencia\(r\) a la que el gameto surge de una combinación de genes de abuela y abuelo. Si los\(B, b\) loci\(A, a\) y ocurren en el mismo cromosoma, entonces\(r\) es la frecuencia de recombinación debido al cruce. Si los\(\mathrm{B}, \mathrm{b}\) loci\(\mathrm{A}, \mathrm{a}\) y ocurren en diferentes cromosomas, entonces debido al surtido independiente de cromosomas existe la misma probabilidad de que el gameto contenga todos los genes de abuelo o abuela, o contenga una combinación de genes de abuela y abuelo, para que\(r=1 / 2\). Observe que el cruce o el surtido independiente es de importancia para aquellos pares de genes para los que la contribución del abuelo y la abuela al genotipo diploide no comparten alelos comunes (es decir,\(A B / a b\) y\(A b / a B\) genotipos). La frecuencia\(p_{A B}^{\prime}\) en la siguiente generación viene dada por la suma de la\(A B\) columna (después de la multiplicación por las frecuencias diploides). Por lo tanto,
\[\begin{align} \nonumber p_{A B}^{\prime} &=p_{A B}^{2}+p_{A B} p_{A b}+p_{A B} p_{a B}+(1-r) p_{A B} p_{a b}+r p_{A b} p_{a B} \\[4pt] \nonumber &=p_{A B}\left(p_{A B}+p_{A b}+p_{a B}+p_{a b}\right)+r\left(p_{A b} p_{a B}-p_{A B} p_{a b}\right) \\[4pt] &=p_{A B}-r D \end{align} \nonumber \]
donde la igualdad final hace uso de\((5.4.2)\) y (5.4.7).
El segundo método para la computación\(p_{A B}^{\prime}\) es más directo. Un\(A B\) haplotipo puede surgir de un diploide de tipo general\(A B / X X\) sin recombinación, o un diploide de tipo\(A X / X B\) con recombinación. Por lo tanto,
\[p_{A B}^{\prime}=(1-r) p_{A B}+r p_{A} p_{B} \nonumber \]
donde el primer término es de no recombinantes y el segundo término de recombinantes. Con\(p_{A} p_{B}=p_{A B}-D\), tenemos
\[\begin{aligned} p_{A B}^{\prime} &=(1-r) p_{A B}+r\left(p_{A B}-D\right) \\[4pt] &=p_{A B}-r D \end{aligned} \nonumber \]
el mismo resultado que\((5.4.9)\).
Usando\((5.4.8)\) y\((5.4.9)\), derivamos
\[D^{\prime}=(1-r) D, \nonumber \]
con la solución
\[D_{n}=D_{0}(1-r)^{n} \nonumber \]
La recombinación disminuye el desequilibrio de ligamiento en cada generación por un factor de\((1-r)\). Los genes estrechamente vinculados en el mismo cromosoma tienen valores pequeños de\(r\); los genes no enlazados en diferentes cromosomas tienen\(r=1 / 2\). Para los genes no enlazados, el desequilibrio de ligamiento disminuye en un factor de dos en cada generación. Concluimos que se requiere una selección muy fuerte para mantener el desequilibrio de ligamiento para genes en diferentes cromosomas, mientras que una selección débil puede mantener el desequilibrio de ligamiento para genes estrechamente vinculados.


