4.1: Derivados elementales

Comenzamos recordando la definición formal, con un ligero ajuste en la notación para que coincida con las convenciones estándar:

Definición\(4.1.1\).

Para una función,\(f(x)\text{,}\) la tasa instantánea de cambio de\(f(x)\text{,}\) o la derivada de\(f(x)\), denotada como\(f'(x)\text{,}\) se define como

\[ f'(x )=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}. \nonumber \]

También queremos recordar algunas anotaciones alternativas que podamos usar.

Notación: Let\(y=f(x)\text{.}\)

La derivada de\(f(x)\) se denota como\(f'(x)\) o\(\frac{d}{dx} f(x) \) o\(dy/dx\text{.}\)

La derivada at\(x=x_0\) se denota como\(f'(x_0 )\) o\(\frac{dy}{dx}|_{x=x_0}\text{.}\)

Como es típico en las matemáticas, cuando hay varias formas, utilizamos la que tiene más sentido en el caso en el que estamos trabajando.

Derivados de los monomios

Nuestra primera regla para la diferenciación simbólica da la derivada de un monomio

Reclamación\(4.1.2\). Monomial Rule.

Si\(f(x)=a x^n\text{,}\) entonces\(f'(x)=n*a*x^{n-1}\text{.}\)

Esta regla es una generalización de la regla que encontramos en la sección 3.2 usando líneas de tendencia. Allí notamos que la derivada es lineal siempre que la función es cuadrática. La regla es válida para todos los valores de n, no solo para números enteros positivos. Ahora podemos encontrar derivados para expresiones que se pueden convertir en esta forma.

Ejemplo\(4.1.3.\) Derivatives of Monomials.

Utilizando nuestra primera regla de diferenciación simbólica, encontramos las derivadas de las siguientes funciones:

1. \(\displaystyle f(x)=3 x\)
2. \(\displaystyle g(x)=5 x^2\)
3. \(\displaystyle h(x)=7x^{25}\)
4. \(\displaystyle j(x)=6 \sqrt{x}\)
5. \(\displaystyle k(x)=\frac{4}{x^3} \)

Solución

Usando nuestra regla:

1. \(\displaystyle \frac{d}{dx} f(x)= \frac{d}{dx} (3 x^1)=1*3 x^0=3.\)
2. \(\displaystyle \frac{d}{dx} g(x)=\frac{d}{dx} (5 x^2 )=2*5 x^1=10 x.\)
3. \(\displaystyle \frac{d}{dx} h(x)=\frac{d}{dx} (7x^{25})=25*7 x^24=175x^{24}.\)
4. \(\displaystyle \frac{d}{dx} j(x)=\frac{d}{dx} (6 \sqrt{x})=\frac{d}{dx} (6x^{1/2} )=1/2*6x^{-1/2}=3x^{-1/2}\)
5. \(\displaystyle \frac{d}{dx} k(x)=\frac{d}{dx} \frac{4 }{x^3 }=d/dx (4 x^{(-3)} )=-3*4 x^{-4}=-12 x^{-4}\)

Para las partes (d) y (e), convertimos raíces y fracciones para que parecieran monomios con exponentes negativos o fraccionarios y aplicamos nuestra regla.

Probablemente la demostración más convincente de la verdad de esta regla es que usemos Excel y las técnicas del último capítulo para encontrar una función, sus derivadas numéricas y simbólicas y ver que las derivadas simbólicas y numéricas son las mismas hasta redondear el error. También nos gustaría ver cómo el derivado simbólico puede derivarse de la definición formal de derivado en casos simples.

Ejemplo 4.1.4: Derivadas de Funciones Lineales.

A partir de la definición formal de derivado, si\(f(x)=a x+b\text{,}\) entonces muestran\(f'(x)=a\text{.}\)

Solución

Usando nuestra definición:

\ begin {reunir*} f' (x) =lim_ {h\ to0}\ frac {f (x+h) -f (x)} {h} =lim_ {h\ to0}\ frac {(a (x+h) +b) - (a x+b)} {h}\\ = lim_ {h\ to0}\ frac {(a x+a h+b) - (a x+b)} {h}\\ = lim_ {h\ to0}\ frac {ah} {h} =lim_ {h\ to0} a=a.\ fin {reunir*}

El último paso se justifica al señalar que a medida que h se vuelve muy pequeño el valor de a simplemente permanece a.

Queremos mirar una función cuadrática, ya que tendremos que tomar un límite en ese caso.

Ejemplo 4.1.5: Una derivada cuadrática.

A partir de la definición formal de derivado, si\(f(x)=a x^2\text{,}\) entonces muestran\(f'(x)=2 a x\text{.}\)

Solución

Usando nuestra definición:

\ begin {reunir*} f' (x) =lim_ {h\ to0}\ frac {f (x+h) -f (x)} {h} =lim_ {h\ to0}\ frac {(a (x+h) ^2) - (a x^2)} {h}\\ = lim_ {h\ to0}\ frac {(a x^2+2 a h x +a h^2) - (a x^2)} {h}\\ =lim_ {h\ to0}\ frac {2 a h x +a h^2} {h} = lim_ {h\ to0} (2ax+h) =2ax. \ end {reunir*}

El último paso se justifica al señalar que a medida que h se vuelve muy pequeño el valor de a h también se vuelve muy pequeño.

Podemos modificar este último ejemplo para encontrar una fórmula para la derivada de\(f(x)=x^n\) para cualquier entero positivo\(n\text{.}\) Recordamos que

\((x+h)^n=x^n+n x^{(n-1)}h+terms\ involving\ h^2.\)

Estamos listos para generalizar.

Ejemplo 4.1.6: Derivada de la Función de Potencia.

A partir de la definición formal de derivado, si\(f(x)=a x^n\text{,}\) entonces muestran\(f'(x)=n a x^{(n-1)}\text{.}\)

Solución

Usando nuestra definición:

\ begin {reunir*} f' (x) =lim_ {h\ to0}\ frac {f (x+h) -f (x)} {h} =lim_ {h\ to0}\ frac {(a (x+h) ^n) - (a x^n)} {h}\\ = lim_ {h\ to0}\ frac {(a (x^n) +n x^ {n-1} h +términos\ que implican\ h^2) - (a x^n)} {h}\\ = lim_ {h\ to0}\ frac {(a (n x^ {n-1} h +términos\ que involucran\ h^2)} {h}\\ = lim_ {h\ to0} (a (n x^ {n-1} +términos\ que involucran\ h) =anx^ {n-1}. \ end {reunir*}

El último paso se justifica al señalar que a medida que h se vuelve muy pequeño el valor de h por un polinomio en h también se vuelve muy pequeño.

Derivadas de Funciones Exponenciales

Reclamación\(4.1.7\). Exponential Rule.

Si\(f(x)=a*e^x\text{,}\) entonces\(f'(x)=a*e^x\text{.}\)

La elegancia de esta regla es parte de la razón por la cual los matemáticos y los libros de matemáticas como base\(e\) para funciones exponenciales. Sin embargo, más típicamente queremos usar funciones exponenciales basadas en una tasa de crecimiento o decaimiento.

Reclamación\(4.1.8\). General Exponential Rule.

Si\(f(x)=b*a^x\text{,}\) entonces\(f'(x)=b*\ln(a)*a^x\text{.}\)

Ejemplo 4.1.9: Regla Exponencial General.

Utilizando las reglas exponenciales de diferenciación simbólica, encuentra las derivadas de las siguientes funciones:

1. \(\displaystyle f(x)=2 e^x\)
2. \(\displaystyle g(x)=\pi e^x\)
3. \(\displaystyle h(x)=7*2^x\)
4. \(\displaystyle j(x)=5*(1.06)^x\)
5. \(\displaystyle k(x)=9*(0.97)^x\)

Solución

Usando nuestra regla:

1. \(\displaystyle \frac{d}{dx} f(x)= \frac{d}{dx} (2 e^x)=2 e^x.\)
2. \(\displaystyle \frac{d}{dx} g(x)=\frac{d}{dx} (\pi e^x )=\pi e^x.\)
3. \(\displaystyle \frac{d}{dx} h(x)=\frac{d}{dx} (7*2^x )=7*\ln(2)*2^x\)
4. \(\displaystyle \frac{d}{dx} j(x)=\frac{d}{dx} (5*(1.06)^x) =5*\ln(1.06)*(1.06)^x \)
5. \(\displaystyle \frac{d}{dx} k(x)=\frac{d}{dx} (9*(0.97)^x) =9*\ln(0.97)*(0.97)^x \)

De alguna manera, el argumento más convincente para estas reglas es usar Excel para trazar la función, su derivada numérica y su derivada simbólica para una variedad de valores y ver que las derivadas numéricas y simbólicas son las mismas hasta el error de redondeo. También quisiéramos hacer un argumento a partir de la definición formal del derivado.

Ejemplo 4.1.10: Justificación de la Primera Regla Exponencial.

De la definición formal de derivado muestran que si\(f(x)=e^x\text{,}\) entonces\(f'(x)=e^x\text{.}\)

Solución

Usando nuestra definición:

\ begin {reunir*} f' (x) =lim_ {h\ to0}\ frac {f (x+h) -f (x)} {h} =lim_ {h\ to0}\ frac {e^ {(x+h)} -e^x} {h}\\ = lim_ {h\ to0}\ frac {e^x (e^h-1)} {h} =e^x\ izquierda (lim_ {h\ to0}\ frac {e^h-1} {h}\ derecha)\ end {reunir*}

.

Basta con mostrar que\(\left(lim_{h\to0}\frac{e^h-1}{h}\right) =1\text{.}\) Esto se puede hacer comenzando con una definición formal de\(e\text{.}\) Para esta clase también se puede hacer usando Excel para evaluar la expresión para valores cada vez más pequeños de h.

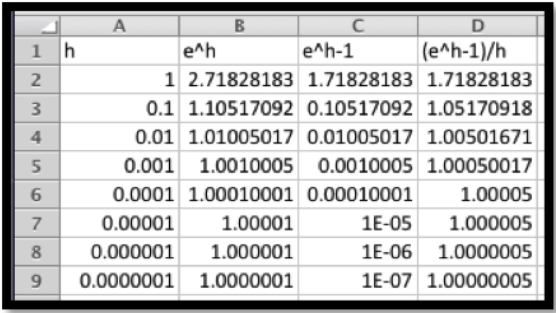
Parece claro que\(\left(lim_{h\to0}\frac{e^h-1}{h}\right) =1\text{.}\)

Ejemplo\(4.1.11.\) Justification of Second Exponential Rule.

A partir de la definición formal de derivado, si\(f(x)=a^x\text{,}\) entonces muestran\(f'(x)=\ln(a)*a^x\text{.}\)

Solución

Empezamos imitando el último problema. En un paso clave\(a^x=e^{x \ln(a)}\text{.}\) recordaremos que También queremos señalar que\(\left(lim_{h\ln(a) \to0}\frac{e^{h\ln(a)}-1}{h\ln(a)}\right) = \left(lim_{h\to0}\frac{e^h-1}{h}\right) =1\text{.}\)

Usando nuestra definición:

\ begin {reunir*} f' (x) =lim_ {h\ to0}\ frac {f (x+h) -f (x)} {h} =lim_ {h\ to0}\ frac {a^ {(x+h)} -a^x} {h}\\ = lim_ {h\ to0}\ frac {a^x (a^h-1)} {h} = (a^x)\ izquierda (lim_ {h\ to0}\ frac {a^h-1} {h}\ derecha)\\ = (a^x)\ izquierda (lim_ {h\ to0} (\ ln (a))\ frac {e^ {h\ ln (a)} -1} {h\ ln (a)}\ derecha)\\ = (a^x\ ln (a))\ izquierda (lim_ {h\ ln (a)\ to0}\ frac {e^ {h\ ln (a)} -1} {h\ ln (a)}\ derecha )\\ = (a^x\ ln (a))\ izquierda (lim_ {h\ to0}\ frac {e^ {h} -1} {h}\ derecha) =a^x\ ln (a)\ end {reunir*}

.

Lo más probable es que veamos funciones exponenciales en el contexto de interés continuamente compuesto.

Ejemplo 4.1.12: Cálculo de la Tasa de Cambio Futura.

Si tengo un dólar en el banco a una tasa de interés anual efectiva del 6%, compuesta continuamente, a qué tasa está aumentando el principal después de años,

Solución

Sabemos\(f(x)=(1.06)^x\text{.}\) Así\(f'(x)=\ln(1.06)(1.06)^x\text{.}\) Evaluamos esto a los 10 años y obtenemos\(f'(10)=\ln(1.06)(1.06)^{10}=.10435074\text{.}\) Así después de 10 años, estoy ganando un poco más de 10 centavos al año.

Derivadas de funciones logarítmicas

Para una última regla para esta sección queremos encontrar la derivada de\(f(x)=a \ln(x)\)

Reclamación\(4.1.13\). Logarithmic Rule.

Si\(f(x)=a \ln(x)\text{,}\) entonces\(f'(x)=a/x\text{.}\)

Ejemplo 4.1.14: Derivadas de Funciones Logarítmicas.

Usando la regla logarítmica de diferenciación simbólica, encuentra las derivadas de las siguientes funciones:

1. \(\displaystyle f(x)=2 \ln(x)\)
2. \(\displaystyle g(x)=3 \ln(x^2)\)
3. \(\displaystyle h(x)=5 \ln(1/x)\)

Solución

Usando nuestra regla:

1. \(\displaystyle \frac{d}{dx} f(x)= \frac{d}{dx} (2 \ln(x))=2/x.\)
2. \(\displaystyle \frac{d}{dx} g(x)=\frac{d}{dx} (3 \ln(x^2))= \frac{d}{dx} (3*2\ln(x))=6/x.\)
3. \(\displaystyle \frac{d}{dx} h(x)=\frac{d}{dx} (5 \ln(1/x))= \frac{d}{dx} (-1*5\ln(x))=-5/x.\)

Nuestro argumento a favor de esta regla derivada será más geométrico.

Ejemplo 4.1.15: Justificación de la regla logarítmica.

Si\(f(x)=\ln(x)\text{,}\) entonces mostrar\(f'(x)=1/x\text{.}\)

Solución

Empezamos notando eso\(y=e^x\) y\(y=\ln(x)\) son funciones inversas. Eso significa que sus gráficos se pueden obtener reflejando a través de la línea\(y=x\text{.}\)

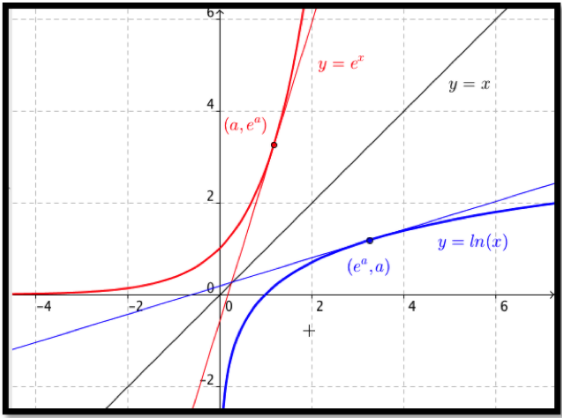
La pendiente de la línea tangente en\((a,e^a)\) es\(e^a\) por la regla exponencial. La simetría nos dice que la pendiente de la línea tangente a\(y=\ln(x)\) at\((e^a,a)\) es\(1⁄e^a\text{.}\) Dejar que\(b=e^a\text{,}\) la pendiente de la línea tangente a\(y=\ln(x)\) at\((b,\ln(b))\) es\(1⁄b\text{.}\) Así\(\frac{d}{dx}(\ln(x))=1/x\text{.}\)

Ejemplo 4.1.16: Pendiente de una Línea Tangente.

Encuentra la pendiente de la línea tangente a\(y=\ln(x)\) al\(x=10\text{.}\) Compara tu respuesta a la estimación dada por las técnicas de aproximación del último capítulo.

Solución

Desde\(f(x)=\ln(x)\text{,}\)\(f'(10) =1/10=.1\text{.}\) Cuando uso Excel para computar\((f(10.001)-f(9.999))/.002\) obtengo\(0.1000000003\text{.}\)

Ejercicios: Problemas de Derivados Elementales

clase=”

Para los ejercicios 1-12, utilice las reglas simbólicas para encontrar la derivada de la función.

Ejercicio 1:

\(f(x)=x^5\text{.}\)

Responder

\[ f(x)=5x^4 \nonumber \]

Ejercicio 2:

\(g(x)=7/x^3\text{.}\)

Ejercicio 3:

\(h(x)=3\sqrt{(x^7)}\text{.}\)

Responder

Reescribir\(h(x)=3x^{7/2}\text{.}\)

\[ h'(x)=\frac{21}{2}(x^{5/2}) \nonumber \]

Ejercicio 4:

\(f(x)=2x^{\pi}\text{.}\)

Ejercicio 5:

\(k(x)=17\text{.}\)

Responder

\[ k'(x)=0 \nonumber \]

Ejercicio 6:

\(m(x)=9x^{-5}\text{.}\)

Ejercicio 7:

\(f(x)=x^2 \sqrt{x}\text{.}\)

Responder

Reescribir\(f(x)=x^{5/2}\text{.}\)

\[ f'(x)=\frac{5}{2}x^{3/2} \text{.} \nonumber \]

Ejercicio 8:

\(g(x)=\ln(x)\text{.}\)

Ejercicio 9:

\(h(x)=e^x\text{.}\)

Responder

\[ h'(x)=e^x \nonumber \]

Ejercicio 10:

\(k(x)=5^x\text{.}\)

Ejercicio 11:

\(m(x)=1.03^x\text{.}\)

Responder

\[ m'(x)=1.03^x\ln(1.03) \nonumber \]

Ejercicio 12:

\(n(x)=(0.9)^x\text{.}\)

Para los ejercicios 13-18, utilice las reglas simbólicas para encontrar la derivada en el punto especificado. Usa Excel para encontrar la aproximación numérica usando la “fórmula de la calculadora”. ¿A cuántos dígitos coinciden los dos métodos?

Ejercicio 13:

\(f(x)=x^2\text{.}\)Evaluar en\(x=2\text{.}\)

Responder

\(f'(x)=2x\text{,}\)entonces\(f'(2)=4\text{.}\) La derivada numérica está de acuerdo con 12 dígitos decimales.

Ejercicio 14:

\(g(x)=5x\text{.}\)Evaluar en\(x=7\text{.}\)

Ejercicio 15:

\(h(x)=1.06^x\text{.}\)Evaluar en\(x=10\text{.}\)

Responder

\(h'(x)=\ln(1.06)(1.06)^x\text{.}\)Entonces\(h'(10)=\ln(1.06)(1.06)^{10}\ (\approx 0.104)\text{.}\) La derivada numérica está de acuerdo con 10 dígitos decimales.

Ejercicio 16:

\(f(x)=e^x\text{.}\)Evaluar en\(x=5\text{.}\)

Ejercicio 17:

\(k(x)=\ln(x)\text{.}\)Evaluar en\(x=100\text{.}\)

Responder

\(k'(x)=1/x\text{.}\)Entonces\(k'(100)=0.01\text{.}\) La derivada numérica está de acuerdo con 13 dígitos decimales.

Ejercicio 18:

\(m(x)=3/x\text{.}\)Evaluar en\(x=\pi\text{.}\)

Encuentra líneas tangentes a las curvas dadas en los puntos indicados.

Ejercicio 19:

\(f(x)=3x^4\text{.}\)En\(x=1\text{.}\)

Responder

Necesitamos un punto: si\(x =1\) entonces\(y=f(1)=3\text{.}\)

Necesitamos una pendiente:\(f'(x)=12 x^3\text{.}\) De ahí\(m=f'(1)=12\text{.}\)

Encuentra la línea:\(y-y_0=m(x-x_0 )\text{,}\) so\(y-3=12(x-1)\text{,}\)

Comentarios

• Podemos reescribir la línea tangente como\(y=12x-9\)
• También podríamos haber usado la versión de intercepción de pendiente de la línea para resolver el problema. Entonces\(y=mx-b\text{.}\) sabemos\(m = 12\text{,}\) y podemos resolver\(b\) por dejar\(x = 1\) y\(y = 3\text{.}\)

Ejercicio 20:

\(g(x)=a x\text{.}\)En\(x=b\text{.}\)

Ejercicio 21:

\(h(x)=1.05^x\text{.}\)En\(x=20\text{.}\)

Responder

Necesitamos un punto: si\(x =20\) entonces\(y=h(20)=(1.05)^20\approx 2.6533\text{.}\)

Necesitamos una pendiente:\(h'(x)=\ln(1.05) (1.05)^x\text{.}\)

De ahí\(m=\ln(1.05) (1.05)^{20}=0.12945\)

Encuentra la línea:\(y-y_0=m(x-x_0 )\text{,}\) so\(y-2.6533=0.12945(x-20)\text{.}\)

Ejercicio 22:

\(f(x)=e^x\text{.}\)En\(x=1\text{.}\)