6.2: Marcos de Alambre, Derivadas Parciales y Planos Tangentes

Última actualización
Guardar como PDF

Page ID: 115941

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una técnica estándar en los cursos de matemáticas es tratar de romper un problema complicado en problemas más pequeños y fáciles. Para funciones de varias variables esto se puede hacer mirando las variables una a la vez, y tratando las otras variables como constantes. Entonces volvemos a considerar funciones de una sola variable. Comenzamos volviendo al Ejemplo 5 de la sección anterior, y viendo qué información se puede obtener mirando una variable a la vez.

Ejemplo 6.2.1: Optimización de Ingresos con Dos Productos.

Tengo una empresa que produce 2 productos, widgets y artilugios. Las dos funciones de demanda son:

\[ PriceGizmos=10-\frac{QuantityGizmos}{50}=10-\frac{QG}{50} \nonumber \]

\[ PriceWidgets=20-\frac{QuantityWidgets}{40}=20-\frac{QW}{40} \nonumber \]

Esto me da la siguiente función de ingresos:

\[ Revenue(QG,QW)=10QG-\frac{QG^2}{50}+20QW-\frac{QW^2}{40}. \nonumber \]

Observa las funciones de una variable obtenida al tratar QG o QW como una constante. Utilice esta información para encontrar dónde maximizamos los ingresos.

Solución

En términos del último ejemplo, queremos comenzar con una tabla y una gráfica de marco de alambre.

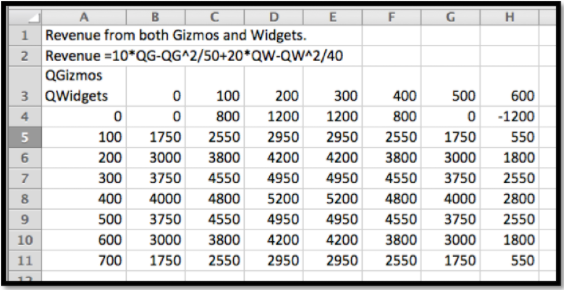
$clipboard_ec126fed0f549653e18c0714ec9d17318.png$

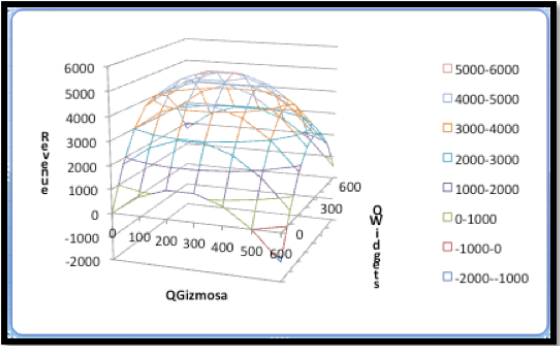
$clipboard_e20c2696feda932ef595e3033db91b45e.png$

Los cables se obtienen intersecando la gráfica de la función con un plano donde QW o QG se mantiene constante.

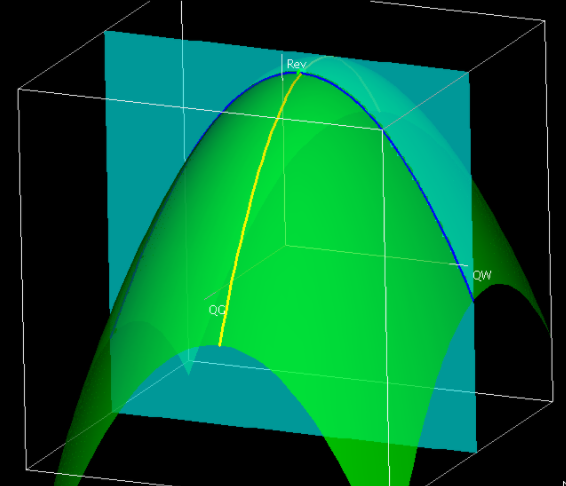
$clipboard_e2e84f8763e0f6f6b008c09b5418a7147.png$

Por lo tanto, cuando tratamos QW o QG como una constante, efectivamente estamos mirando uno de los cables del marco de alambre. Para ilustrar esto, veremos los cables correspondientes a$QW=400$ y$QG=300\text{.}$ Cuando$QG=300\text{,}$ nuestra función de ingresos se simplifica a

\[ \begin{aligned} Revenue(300,QW) \amp =3000-1800+20QW-\frac{QW^2}{40}\\ \amp =1200+20QW-\frac{QW^2}{40}.\end{aligned} \nonumber \]

Así, el alambre correspondiente a$QG=300$ es una parábola que se dobla hacia abajo.

El siguiente interactivo muestra cómo se construye la estructura alámbrica a partir de cubas definidas por curvas de corte definidas por planos de corte.

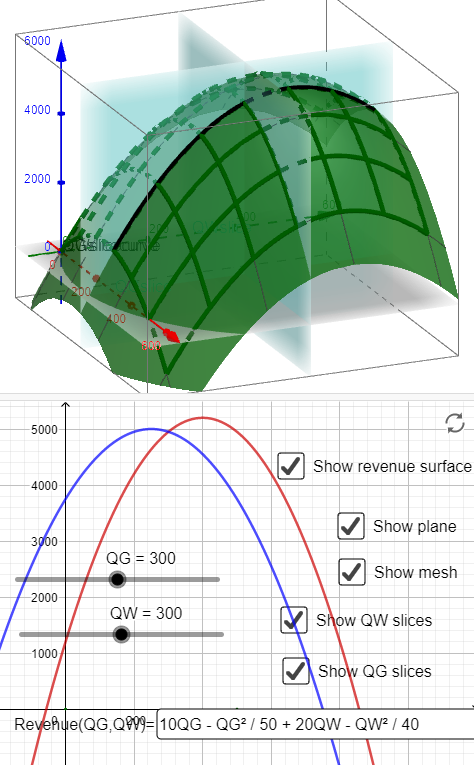
$clipboard_e3b2a36546355fd68ee6ee522548c838a.png$

Figura Malla$6.2.2.$ de alambre

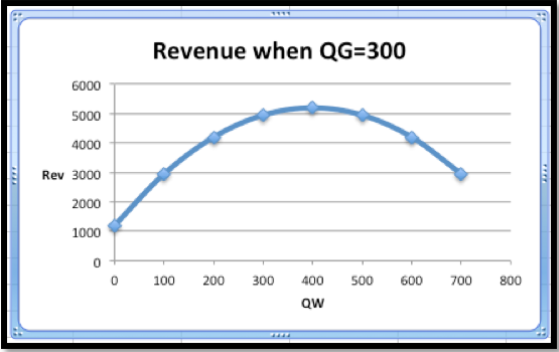
$clipboard_eb4f46c5fed85bca504072a9c491e0d7c.png$

Para encontrar el vértice de la parábola, tomamos la derivada de nuestra función de QW y la ponemos igual a cero.

\[ \frac{d}{d\ QW} Revenue(300,QW)=20-\frac{QW}{20}. \nonumber \]

Esta derivada es cero cuando$QW=400\text{.}$ Ese es el único lugar posible en este cable donde podamos tener un máximo.

Del mismo modo, cuando$QW=400\text{,}$

\[ Revenue(QG,400)=10QG-\frac{QG^2}{50}+4000, \nonumber \]

\[ \frac{d}{d\ QG} Revenue(QG,400)=10-\frac{QG}{25}. \nonumber \]

Esta derivada es cero cuando$QG=250\text{.}$ Ese es el único lugar posible en este cable donde podamos tener un máximo.

Al juntar la información, el máximo debe ocurrir en (250,400). Volver a poner estos valores en la ecuación original da un máximo de 5250 dólares para la función de ingresos.

Derivadas Parciales

El procedimiento que usamos en el primer ejemplo de reemplazar una variable por una constante y luego tomar la derivada de la función de variable única resultante es un poco engorroso. Podemos simplificar el proceso tomando la derivada de la función original con respecto a una variable mientras tratamos las otras variables como constantes. Esto se conoce como tomar una derivada parcial. También hay un cambio en la notación. La derivada familiar de$f$ con respecto a$x$ usa el símbolo$\frac{d}{dx} f$ mientras que la derivada parcial con respecto a$x$ usa el símbolo$\frac{\partial }{\partial x} f\text{,}$ o$f_x\text{.}$ De manera similar, la derivada parcial con respecto a$y$ usa el símbolo$\frac{\partial }{\partial y} f\text{,}$ o$f_y\text{.}$

Ejemplo 6.2.3: Encontrar e Interpretar Derivadas Parciales.

Encuentra las derivadas parciales de$f(x,y)=x^2+ 2xy+3y^2-4x-3y$ en$(x,y)=(3.5,-0.5)\text{.}$ Explicar qué significan las derivadas parciales en términos de la gráfica.

Solución

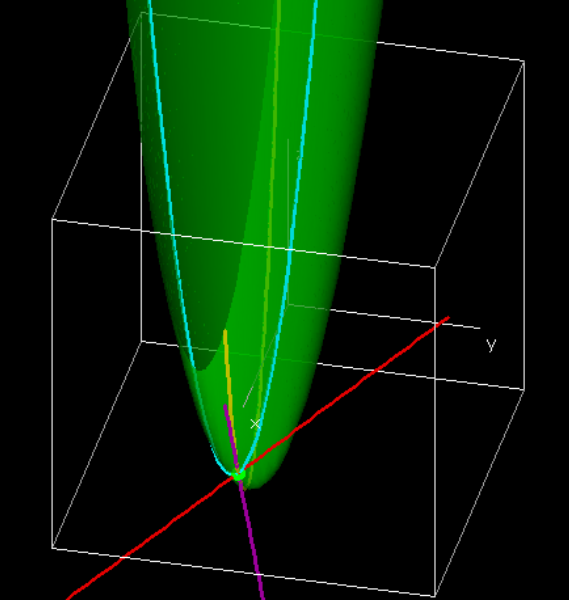
Es útil observar una imagen con la gráfica, las dos curvas obtenidas manteniendo$x=3.5$ y$y=1.5\text{,}$ y las líneas tangentes a esas curvas.

$clipboard_edf523e588895ec9ecc95823ea4a72e3c.png$

También queremos ver las rebanadas correspondientes manteniendo$x=-3.5$ y$y=.5\text{.}$

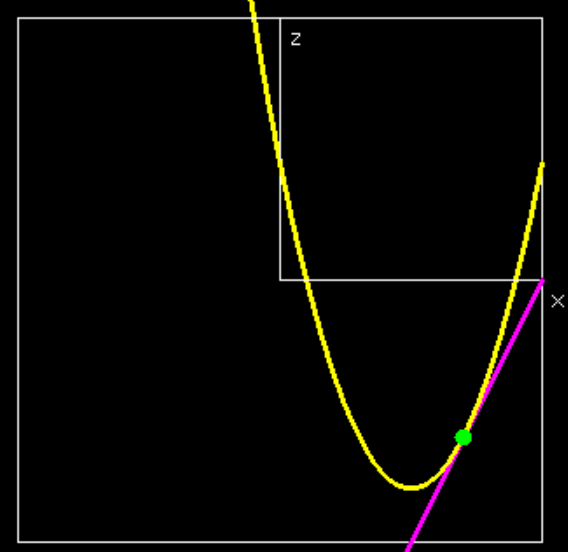
$clipboard_e9d3d2c9d9012b8577444d37c424cbec2.png$

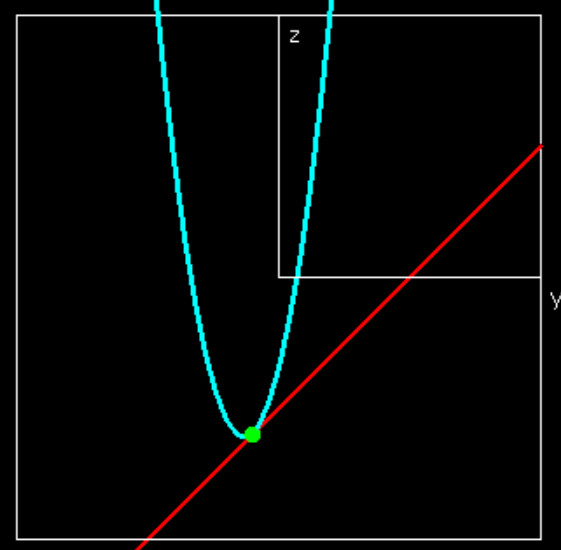
$clipboard_e9ceb678342cd1ddfa8f0efc4b3966104.png$

La curva amarilla se obtiene fijando$y$ y dejando$x$ variar. La curva azul se obtiene fijando$y$ y dejando$x$ variar. Ahora tomamos las derivadas parciales con respecto a ambas variables.

\[ \frac{\partial }{\partial x} f(x,y)=2x+ 2y+0-4-0=2x+2y-4. \nonumber \]

\[ \frac{\partial }{\partial x} f(3.5,-0.5)=7- 1-4=2. \nonumber \]

\[ \frac{\partial }{\partial y} f(x,y)=0+2x+6y+0-3=2x+6y-3. \nonumber \]

\[ \frac{\partial }{\partial y} f(3.5,-0.5)=7-3-3=1. \nonumber \]

Las derivadas parciales dan las pendientes de las líneas púrpura y roja arriba. En el punto$(3.5,-0.5)\text{,}$ las curvas (amarillas) obtenidas al tratar y como una constante y dejar$x$ variar tiene una línea tangente (magenta) con una pendiente$2\text{,}$ del valor$\frac{\partial }{\partial x} f(3.5,-0.5)\text{.}$ En el punto$(3.5,-0.5)\text{,}$ las curvas (azules) obtenidas al tratar$x$ como una constante y dejar$y$ variar tiene un (roja) línea tangente con una pendiente de 1, el valor$\frac{\partial }{\partial y} f(3.5,-0.5)\text{.}$

Planos tangentes y aproximación lineal

Para las funciones de una variable, tuvimos dos usos principales de la derivada. Una fue identificar puntos candidatos para máximos y mínimos. Veremos puntos críticos y extremos en la siguiente sección. El otro uso de la derivada fue producir una aproximación lineal o línea tangente. Podemos generalizar la línea tangente para una variable a un plano tangente para dos variables. Para una función$f(x)\text{,}$ usamos el valor del punto,$(x_0,f(x_0))$ y la pendiente$f(x_0)$ para obtener la ecuación de la aproximación de la línea tangente cerca$x_0\text{.}$

Línea tangente:

\[ Linear f(x)=f' (x_0 )(x-x_0 )+f(x_0 ). \nonumber \]

Para una función,$f(x,y)\text{,}$ de dos variables, simplemente usamos parciales para las pendientes.

Plano tangente:

\[ Linear f(x ,y)=f_x (x_0,y_0 )(x-x_0 )+f_y (x_0,y_0 )(y-y_0)+f(x_0,y_0 ). \nonumber \]

Ejemplo 6.2.4: Aproximación con un Plano Tangente.

La función general de producción Cobb-Douglas determina la Producción (P), en términos de las variables Trabajo (L) y Capital (C):

\[ Production(Labor,Capital)=c Labor^{\alpha} Capital^{\beta}, \nonumber \]

o usando notación de mano corta:

\[ P(L,C)=c L^{\alpha} C^\beta, \nonumber \]

donde$c\text{,}$$\alpha\text{,}$ y$\beta$ son constantes. Para nuestra fábrica de widgets, esto se convierte en

\[ Production(Labor,Capital)=10 L^{0.75} C^{0.25} \nonumber \]

con producción de mano de obra y capital en las unidades correspondientes. Buscar$Production(81,16)\text{.}$ Usar una aproximación lineal para estimar$Production(85,14)\text{.}$

Solución

Respondemos a la primera pregunta sustituyendo los valores en la ecuación.

\[ Production(81,16)=10*81^{0.75}*16^{0.25}=10*27*2=540. \nonumber \]

Para producir el plano tangente tomamos las derivadas parciales y las evaluamos en nuestro punto base.

\[ Production_{Labor} (Labor,Capital)=10*.75 Labor^{-0.25} Capital^{0.25} \nonumber \]

\[ Production_{Labor} (81,16)=10*.75 (1/3) *2=5 \nonumber \]

\[ Production_{Capital} (Labor,Capital)=10*{0.25} Labor^{0.75 } Capital^{-0.75} \nonumber \]

\[ Production_{Capital} (81,16)=10*.25 *27 (1/8)=8.4375 \nonumber \]

Esto nos da nuestro plano tangente.

\[ Production(Labor,Capital)\approx5(Labor-81)+8.4375(Capital-16)+540. \nonumber \]

Sustituir en valores da nuestra estimación.

\[ Production(85,14)\approx 5(85-81)+8.4375(14-16)+540=543.125. \nonumber \]

En el caso del último ejemplo, evaluar la aproximación lineal fue mejor que evaluar la función directamente porque las 4tas raíces de 16 y 81 son números enteros, mientras que las 4tas raíces de 85 y 14 son más difíciles de calcular. Para las funciones del mundo real, evaluar funciones puede implicar una inversión sustancial de tiempo y dinero, dependiendo de la naturaleza de la función.

Aproximaciones lineales de funciones de más de dos variables

En esta sección nos hemos centrado en funciones de 2 variables ya que sus gráficas son superficies en 3 dimensiones, lo cual es un concepto familiar. Para las funciones del mundo real, a menudo nos preocupan funciones de muchas variables. El concepto de derivada parcial se extiende fácilmente, con una variable y múltiples parámetros. Encontrar la aproximación lineal también se extiende sin dificultad. Simplemente tenemos un término lineal para cada variable.

clase=”

Ejercicios: Problemas de Marcos de Alambre, Derivadas Parciales y Planos Tangentes

Para los ejercicios 1-7, para las funciones y puntos dados$P_1$ y$P_2\text{:}$

Dar las 2 funciones de una variable a través de$P_1$ obtenidas manteniendo cada variable constante.
Encuentra las derivadas parciales de la función original.
Evaluar las derivadas parciales en$P_1\text{.}$
Dar la ecuación del plano tangente a través de$P_1\text{.}$
La aproximación a$P_2$ obtenida del plano tangente.

Ejercicio 1:

La función es$f(x,y)=x^2+3xy+4y^2\text{,}$$P_1=(4,2)\text{,}$ y$P_2=(3,2.5)\text{.}$

Contestar

Dar las 2 funciones de una variable a través de$P_1$ obtenidas manteniendo cada variable constante.
\[ f(4,y)=16+12y+4y^2 \nonumber \]

\[ f(x,2)=x^2+6x+16 \nonumber \]