6.3: Puntos Críticos y Extremos
- Page ID
- 115947
Con funciones de una variable nos interesaron los lugares donde la derivada es cero, ya que hicieron puntos candidatos para el máximo o mínimo de una función. Si la derivada no es cero, tenemos una dirección que es cuesta abajo y moverse un poco en esa dirección da un menor valor de la función. De igual manera, con funciones de dos variables solo podemos encontrar un mínimo o máximo para una función si ambas derivadas parciales son 0 al mismo tiempo. Tales puntos se denominan puntos críticos.
El punto\((a,b)\) es un punto crítico para la función multivariable\(f(x,y)\text{,}\) si ambas derivadas parciales son 0 al mismo tiempo.
En otras palabras
\[ \frac{\partial }{\partial x} f(x,y)|_{x=a,y=b}=0 \nonumber \]
y
\[ \frac{\partial }{\partial y} f(x,y)|_{x=a,y=b}=0 \nonumber \]
Utilice las derivadas parciales de\(f(x,y)=x^2+ 2xy+3y^2-4x-3y\) para encontrar el mínimo de la gráfica.
Solución
Punto Crítico por Álgebra: En la sección anterior, ya calculamos
\[ \frac{\partial }{\partial x} f(x,y)=2x+2y-4 \nonumber \]
\[ \frac{\partial }{\partial y} f(x,y)=2x+6y-3. \nonumber \]
Necesitamos encontrar los lugares donde ambas derivadas parciales son 0. Con este sencillo sistema, puedo resolver este sistema algebraicamente y encontrar el único punto crítico es\((9/4, -1/4)\text{.}\)
\[ 0=2x+2y-4 \nonumber \]
\[ 0=2x+6y-3 \nonumber \]
Restar las ecuaciones para eliminar\(x\text{.}\)
\[ 0=0-4y-1 \nonumber \]
Resolver para\(y\text{.}\)
\[ 4y=-1 \nonumber \]
\[ y=-1/4 \nonumber \]
Sustituir la espalda y resolver\(x\text{.}\)
\[ 0=2x+2(-1/4)-4 \nonumber \]
\[ 2x=9/2 \nonumber \]
\[ x=9/4 \nonumber \]
Punto Crítico por Solver: Sin embargo, si los parciales son más complicados, voy a querer encontrar los puntos críticos de otra manera. Puedo encontrar el punto con Solver.
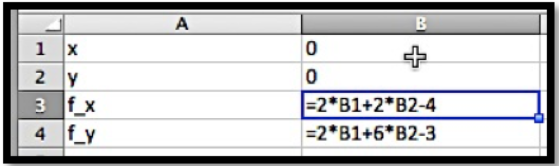

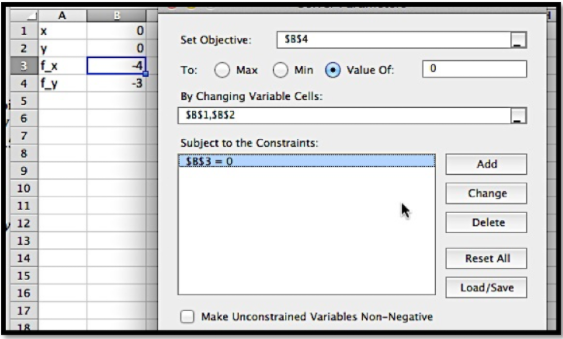
Para que solver establezca ambos parciales en 0 al mismo tiempo, le pido que resuelva por\(f_y=0\text{,}\) mientras establece\(f_x=0\) como restricción. Asegúrese de desmarcar la casilla que hace que las variables no restringidas no sean negativas.

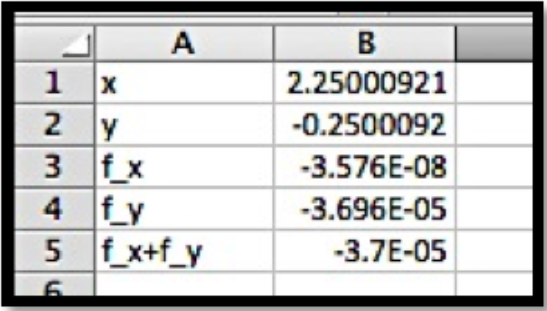
Esto encuentra nuestro punto crítico dentro de nuestra tolerancia a errores.

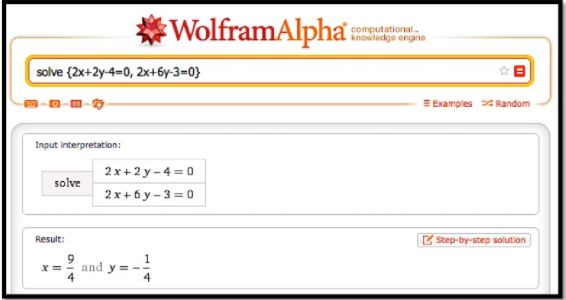
Critical Point by CAS: También podemos usar Wolfram|Alpha para encontrar la solución a nuestro sistema de ecuaciones.

Determinar el Punto Crítico es un Mínimo Obtenemos así un punto crítico en (9/4, -1/4) con cualquiera de los tres métodos de resolución para ambas derivadas parciales siendo cero al mismo tiempo. Una vez que tenemos un punto crítico queremos determinar si es un máximo, mínimo, o algo más. La forma más fácil es mirar la gráfica cerca del punto crítico.

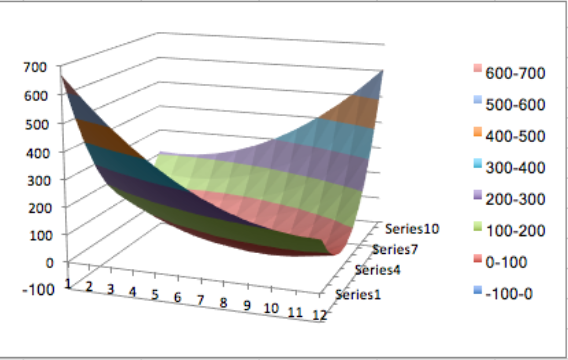
De la gráfica queda claro que este punto crítico es un mínimo local.
Es fácil ver que\(f(x,y)=x^2+y^2\) tiene un punto crítico en\((0,0)\) y que ese punto es mínimo para la función. De igual manera,\(f(x,y)=-x^2-y^2\) tiene un punto crítico en\((0,0)\) y ese punto es un máximo para la función. Para algunas funciones, como\(f(x,y)=x^2-y^2\text{,}\) que tiene un punto crítico en\((0,0)\text{,}\) podemos tener un máximo en una dirección y un mínimo en otra dirección. Tal punto se llama punto de silla de montar. Observamos que podemos tener un punto de sillín aunque las curvas\(x\) y\(y\) slice indiquen un mínimo.
Mostrar que\(f(x,y)=x^2-3xy+y^2\) tiene un punto crítico en el\((0,0)\text{,}\) que es un mínimo de ambas curvas de corte, pero no es un mínimo local.
Solución
Observamos las dos derivadas parciales, y notamos que ambas son cero en el origen.
\[ \frac{\partial }{\partial x} f(x,y)=2x-3y \nonumber \]
\[ \frac{\partial }{\partial x} f(x,y)=-3x+2y. \nonumber \]
Entonces vemos que ambas curvas de corte son parábolas que se doblan hacia arriba, con un mínimo a 0.
\[ f(x,0)=x^2 \nonumber \]
\[ f(0,y)=y^2. \nonumber \]
Sin embargo si llevamos la rebanada con\(x=y\text{,}\) obtenemos una parábola agachándose, así no tenemos un mínimo.
\[ f(x,-x)=x^2-3x x+x^2=-x^2. \nonumber \]
Al mirar la gráfica, vemos que esta gráfica no tiene un mínimo.

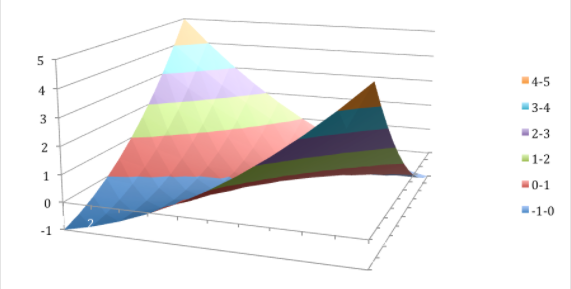
Con solo primeras derivadas, solo podemos encontrar los puntos críticos. Para verificar si un punto crítico es máximo, mínimo o punto de sillín, usando solo la primera derivada, el mejor método es mirar una gráfica para determinar el tipo de punto crítico. Para algunas aplicaciones queremos categorizar simbólicamente los puntos críticos.
Segunda Derivadas Parciales
Con funciones de una variable se utilizó la segunda derivada para probar si un punto crítico era máximo o mínimo. En el caso de dos variables necesitamos definir las segundas derivadas y utilizarlas para definir el discriminante de una función para probar si un punto crítico es mínimo, máximo o punto de sillín. Primero necesitamos definir segundas derivadas parciales.
Segundos parciales:
\[ f_{ab}=(f_a )_b=\frac{\partial}{\partial b}(\frac{\partial}{\partial a} f). \nonumber \]
Tenga en cuenta que\(f_{xx}\) es simplemente la segunda derivada antigua de la curva\(f(x,y_0)\) y\(f_{yy}\) es simplemente la segunda derivada antigua de la curva\(f(x_0,y)\text{.}\) Para las curvas con segundas derivadas parciales continuas, las parciales mixtas,\(f_{yx}\) y\(f_{xy}\) son las mismas.
Encuentra las segundas derivadas parciales de
\[ f(x,y)=x^2+ 3xy+5y^3-7x-11y. \nonumber \]
Solución
Comenzamos por computar las primeras derivadas parciales.
\[ f_x=\frac{\partial}{\partial x} f(x,y)=2x+3y-7 \nonumber \]
\[ f_y=\frac{\partial}{\partial y} f(x,y)=3x+15y^2-11. \nonumber \]
Después calculamos las segundas derivadas parciales.
\[ f_{xx}=\frac{\partial}{\partial x} f_x=2 \nonumber \]
\[ f_{xy}=\frac{\partial}{\partial y} f_x=3 \nonumber \]
\[ f_{yx}=\frac{\partial}{\partial x} f_y=3 \nonumber \]
\[ f_{yy}=\frac{\partial}{\partial y} f_y=30y \nonumber \]
Como era de esperar, los parciales mixtos son los mismos.
Uso del discriminante para probar puntos críticos
Para probar si un punto crítico es un punto máximo, mínimo o sillín calculamos el discriminante de la función.
Discriminante:
\[ D(f(x,y))=f_{xx} f_{yy}-f_{xy}^2. \nonumber \]
Encuentra al discriminante de
\[ f(x,y)=x^2+ 3xy+5y^3-7x-11y. \nonumber \]
Solución
Ya hemos calculado las segundas derivadas parciales.
\[ f_xx=2,\quad f_xy=3,\quad f_yy=30y. \nonumber \]
Sustituyendo en la fórmula
\[ D=(2)(30y)-3^2=60y-9. \nonumber \]
Prueba discriminante: Dejar\((a,b)\) ser un punto crítico de\(f(x,y)\text{.}\)
Si\(D(a,b)>0\) y\(f_{xx} (a,b)>0\) entonces\((a,b)\) es un mínimo local de\(f(x,y)\text{.}\)
Si\(D(a,b)>0 \) y\(f_{xx} (a,b)\lt 0\) entonces\((a,b)\) es un máximo local de\(f(x,y)\text{.}\)
Si\(D(a,b)\lt 0\) entonces\((a,b)\) es un punto de sillín de\(f(x,y)\text{.}\)
Si no\(D(a,b)=0\) tenemos suficiente información para clasificar el punto.
Con base en la información proporcionada, clasifique cada uno de los siguientes puntos como máximo local, mínimo local, punto de sillín, no punto crítico, o no suficiente información para clasificar.
| p | \({f_x}\) | \({f_y}\) | \(f_{xx}\) | \(f_{xy}\) | \(f_{yy}\) |
| A | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 1 | 3 | 2 | 4 |
| C | 1 | 0 | 0 | 2 | 3 |
| D | 0 | 0 | 1 | 2 | 0 |
| E | 0 | 0 | -1 | 2 | 3 |
| F | 0 | 0 | -3 | 1 | -2 |
| G | 0 | 0 | 3 | 3 | 3 |
Solución
Necesitamos calcular el discriminante y aplicar la prueba.
| p | \(f_x\) | \(f_y\) | \(f_{xx}\) | \(f_{xy}\) | \(f_{yy}\) | Discriminante | Clasificación |
| A | 0 | 0 | 0 | 0 | 1 | 0 | No hay suficiente información |
| B | 0 | 1 | 3 | 2 | 4 | 8 | No es un punto crítico |
| C | 1 | 0 | 0 | 2 | 3 | -4 | No es un punto crítico |
| D | 0 | 0 | 1 | 2 | 0 | -4 | Punto de sillín |
| E | 0 | 0 | -1 | 2 | 3 | -7 | Punto de sillín |
| F | 0 | 0 | -3 | 1 | -2 | 5 | Máximo |
| G | 0 | 0 | 3 | 3 | 3 | 0 | No hay suficiente información |
Vamos a\(f(x,y)=x^3-3x+y^3-3y^2\text{.}\) encontrar los puntos críticos y clasificarlos usando el discriminante.
Solución
Comenzamos por computar las primeras derivadas parciales.
\[ f_x=3x^2-3=3(x-1)(x+1) \nonumber \]
\[ f_y=3y^2-6y=3(y-2)(y). \nonumber \]
Después calculamos las segundas derivadas parciales y las discriminantes.
\[ f_{xx}=6x,\quad f_{xy}=0,\quad f_{yy}=6y-6,\quad D=(6x)(6y-6)-0^2=36xy-36x. \nonumber \]
Tenemos puntos críticos cuando ambos primeros parciales son 0, entonces at\((1,2)\text{,}\)\((-1,2)\text{,}\)\((1,0)\text{,}\) y\((-1,0)\text{.}\)
En\((1,2)\text{,}\) ambos\(D\) y\(f_{xx}\) son positivos, por lo que tenemos un mínimo local.
En\((-1,2)\) y\((1,0)\text{,}\)\(D\) es negativo, así que tenemos un punto de sillín.
At (\((-1,0)\text{,}\)\(D\)es positivo y\(f_{xx}\) es negativo, por lo que tenemos un máximo local.
Ejercicios: Puntos Críticos y Problemas Extremos
clase=”Para los ejercicios 1-6, para las funciones y región dadas:
- Encuentra las derivadas parciales de la función original.
- Encuentra cualquier punto crítico en la región.
- Produzca una pequeña gráfica alrededor de cualquier punto crítico.
- Determine si los puntos críticos son máximos, mínimos o puntos de sillín.
La función es\(f(x,y)=x^2+2xy+4y^2+5x-6y\text{,}\) para la región\(-10\le x\le 10\text{,}\) y\(-10\le y\le 10\text{.}\)
- Contestar
-
- \[ f_x (x,y)=2x+2y+5 \nonumber \]


