6.4: Optimización y mejor ajuste de curvas
- Page ID
- 115948
En la última sección analizamos el uso de las derivadas parciales para encontrar el máximo o mínimo de una función en varias variables. Esto es una extensión de los problemas de optimización que hicimos con funciones de una sola variable. Vale la pena echar otro vistazo a las curvas o líneas de tendencia que mejor se ajustan, un proceso que Excel ha estado haciendo a lo largo del curso y ver que es un ejemplo particular de optimización. Esto nos permitirá ajustar mejor las curvas que utilizan modelos distintos a los utilizados por el comando de línea de tendencia.
Definición de la mejor curva de ajuste
Antes de que podamos encontrar la curva que mejor se ajuste a un conjunto de datos, necesitamos entender cómo se define el “mejor ajuste”. Comenzamos con el ejemplo no trivial más simple. Consideramos un conjunto de datos de 3 puntos,\({(1,0),(3,5),(6,5)}\) y una línea que usaremos para predecir el valor y dado el valor x,\(predicted(x)=x/2 +1\text{.}\) queremos determinar qué tan bien coincide la línea con esos datos. Para cada punto,\((x_0,y_0)\text{,}\) en el conjunto comenzamos por encontrar el punto correspondiente,\((x_0,predicted(x_0 ))\text{,}\) en la línea. Esto nos da un conjunto de puntos predichos,\({(1,1.5),(3,2.5),(6,4)}\text{.}\)

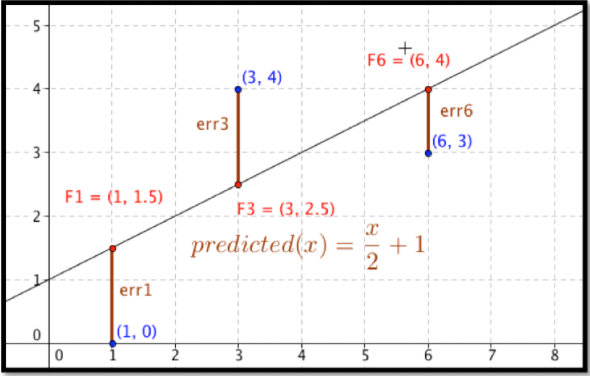
Para cada punto ahora calculamos la diferencia entre los valores y reales y los valores y predichos. Nuestros errores son las longitudes de los segmentos marrones en la imagen, en este caso\({3/2,3/2,1}\text{.}\) Finalmente agregamos los cuadrados de los errores,\(9/4+9/4+1=11/2\text{.}\)
La línea de mejor ajuste se define como la línea que minimiza la suma de los cuadrados del error. Si estamos tratando de ajustar los datos con un modelo diferente queremos elegir la ecuación de ese modelo que minimice la suma de los cuadrados del error.
Ahora que tenemos una definición queremos mirar ajustar una línea a un conjunto de datos simple de tres maneras. Comenzaremos con el conjunto de datos de tres puntos:
| x | 2 | 4 | 8 |
| y | 1 | 15 | 15 |
Queremos comenzar con el método familiar, usando el comando trendline de una gráfica. Entonces queremos usar solver para minimizar la suma de errores cuadrados. Finalmente queremos mirar la función para suma de errores cuadrados para ver cómo encontramos la línea usando derivadas parciales. Después de haber mirado los tres enfoques para este primer ejemplo consideraremos ejemplos más complicados.
Utilice el comando de línea de tendencia para encontrar la mejor línea de ajuste para los datos:
| x | 2 | 4 | 8 |
| y | 1 | 15 | 15 |
Solución
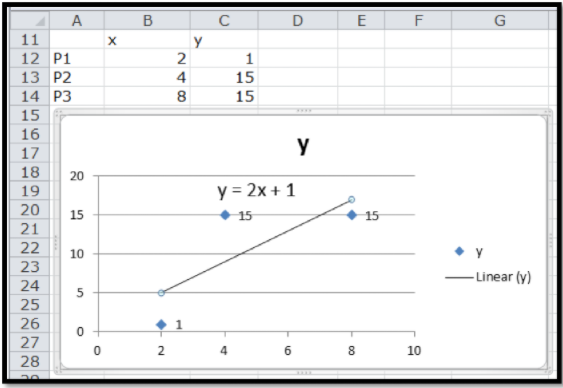
Comenzamos haciendo una tabla agregando una gráfica de dispersión y agregando una línea de tendencia a la gráfica. Recordamos seleccionar la opción para hacer visible la fórmula. El comando de línea de tendencia nos dice que la pendiente debe ser 2 y la intercepción debe ser 1.
Utilice el solucionador y la definición de mejor ajuste para encontrar la mejor línea de ajuste para los datos:
| x | 2 | 4 | 8 |
| y | 1 | 15 | 15 |
Solución
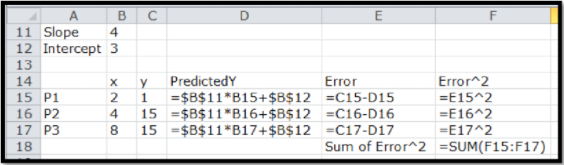
Para usar solver necesitamos agregar la ecuación predictora. Comenzamos con una pendiente escogida aleatoriamente e interceptamos para nuestra línea de predicción. Nuestra tabla tiene una columna PredicteDy, que da el valor que estaría en la línea con nuestra pendiente e intercepción. Agregamos en el error, que es la diferencia entre la y predicha y y real, y el cuadrado del error. Luego tomamos la suma de los cuadrados de los errores.

Nuestro uso de Solver es similar a cuando buscábamos un mínimo de una función de una variable. Necesitamos designar la celda con el valor que queremos minimizar. Seleccionamos el botón para minimizar. Ahora designamos dos celdas que representan variables que podemos cambiar.

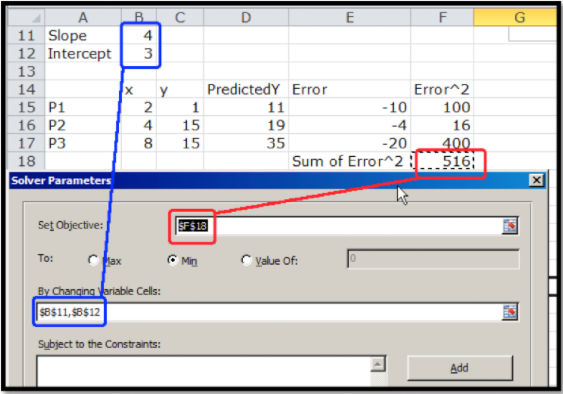
Solver produce la misma respuesta. La mejor línea de ajuste es
\[ y=2x+1. \nonumber \]
Utilice el cálculo, las derivadas parciales y la definición de mejor ajuste para encontrar la mejor línea de ajuste para los datos:
| x | 2 | 4 | 8 |
| y | 1 | 15 | 15 |
Solución
Antes de que podamos usar derivadas parciales para encontrar una línea de mejor ajuste, necesitamos una función cuyas derivadas estamos tomando. Comenzamos con el gráfico que producimos cuando estábamos usando solver. Esto da una fórmula para el error cuadrado en cada punto en términos de la pendiente e intercepción de la línea.
| Punto | x | y | Y Predictado | \(error\) | \(error^2\) |
| \(P1\) | \(2\) | \(1\) | \(m*2+b\) | \(m*2+b-1\) | \((m*2+b-1)^2\) |
| P2 | 4 | 15 | m*4+b | m*4+b-15 | (m*4+b-15) |
| P3 | 8 | 15 | m*8+b | m*8+b-15 | \((m*8+b-15)^2\) |
Podemos ampliar el término de error al cuadrado y sumar esos valores. Después de un cálculo sencillo pero tedioso, vemos que estamos tratando de minimizar
\[ SumErrorSq(m,b)=84m^2+28mb+3b^2-62b-364m+451. \nonumber \]
Tomamos la derivada parcial de esta función con respecto a la pendiente\(m\) y la intercepción\(b\text{.}\)
\[ SumErrorSq_m (m,b)=168m+28b-364. \nonumber \]
\[ SumErrorSq_b (m,b)=28m+6b-62. \nonumber \]
Estableciendo los dos parciales a cero y resolviendo vemos que los parciales son ambos cero cuando\(m=2\) y\(b=1\text{.}\) One nuevamente, este método produce la misma línea de mejor ajuste.
Podemos usar los mismos métodos con un problema mayor.
En la siguiente tabla se dan datos censales para una colección de 10 estados. Encuentre la mejor línea de ajuste para predecir la población del 2010 con base en la población de 2000.
| Pop 2000 | Pop 2010 | |
| Wyoming | 493,782 | 563,62 |
| Delaware | 783,600 | 897,934 |
| Maine | 1,274,923 | 1,328,361 |
| Nevada | 1,998,257 | 2,700,551 |
| Iowa | 2,926,324 | 3,046,355 |
| Kentucky | 4,041,769 | 4,339,367 |
| Arizona | 5,130,632 | 6,392,017 |
| Washington | 5,894,121 | 6,724,540 |
| Nueva Jersey | 8,414,350 | 8,791,894 |
| California | 33,871,648 | 37,253,956 |
Solución
Configuramos una hoja de cálculo de la misma manera que la configuramos en el último ejemplo. Para una pendiente inicial comenzaremos con 1.1 para un crecimiento del 10%. Para un punto de partida adivinaremos una intercepción de 0. Como hicimos en el último ejemplo, la población pronosticada en 2010 es la pendiente multiplicada por la población en 2000 más la intercepción. Agregamos columnas adicionales para la población pronosticada, el error entre la predicción y la población real, el cuadrado del error. En la parte inferior de la última columna, agregamos los errores al cuadrado. Esto da el valor que queremos minimizar.

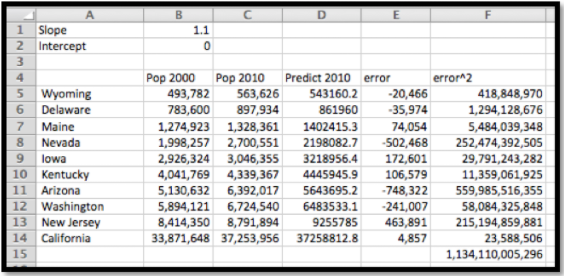
Cuando usamos solver, la mejor línea de ajuste es
\[ 2010population=1.096*2000population+98,154. \nonumber \]
La ventaja de usar la definición de suma de cuadrados es que podemos encontrar una curva de mejor ajuste usando un modelo no soportado por Excel. Por ejemplo, si tenemos dinero invertido con intereses, pero una porción del capital mantenido disponible como efectivo sin ganar intereses, estamos buscando una curva de la forma:
\[ TotalValue(time)=CashAmount+DepositAmount*rate^{time}. \nonumber \]
El comando de línea de tendencia no nos permite elegir dicho modelo para encontrar la mejor curva de ajuste. Es sencillo usar la construcción de mejor ajuste.
Se nos dan los siguientes datos sobre el valor de una cartera a lo largo del tiempo:
| Año | Monto |
| 0 | $10,000 |
| 2 | 10,920 |
| 5 | $12,490 |
| 8 | 14,300 |
| 9 | $14,960 |
| 12 | $17,169 |
| 14 | $18,820 |
| 17 | 21,630 |
| 19 | 23,740 |
| 20 | $24,880 |
Pensamos que el inversionista puso algo de dinero en una cuenta segura que no da intereses (una lata de café) y el resto del dinero en una cuenta que tenía intereses (una cuenta de inversión). Encuentra el monto depositado en cada cuenta y la tasa de interés de la cuenta de inversión.
Solución
Configuramos esto como lo hicimos para el modelo lineal, excepto de la ecuación del modelo es ahora
\[ TotalValue(time)=CashAmount+DepositAmount*rate^{time}. \nonumber \]

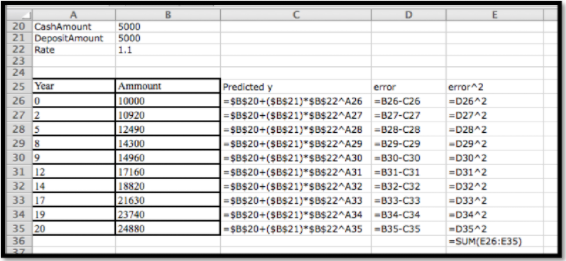
Luego usamos Solver para minimizar la celda E26, cambiando las celdas B20:B22. Nuestra solución indica que Cashamount=$997.76, Depositamount=$9,005.51, y tasa=1.05.
Cuando usamos esta técnica con otros modelos matemáticos, el único cambio está en la fórmula utilizada para el valor y predicho.
Estamos manejando un negocio de cosecha de madera. El número de árboles disponibles en una parcela se modela como crecimiento restringido. Eso significa que esperamos que sea modelada por una ecuación logística.
\[ AvailableTrees(time)=Capacity/(1+C*e^((-rate*time)) ) \nonumber \]
Tenemos la siguiente información. Encuentra la mejor curva de ajuste.
| Tiempo | Árboles |
| 0 | 150 |
| 5 | 400 |
| 10 | 1030 |
| 20 | 5300 |
| 30 | 12020 |
| 40 | 14510 |
Solución
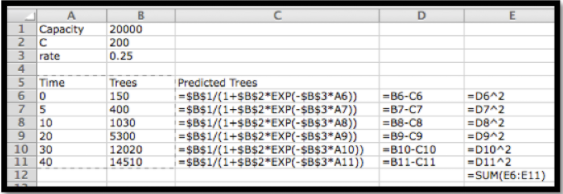
Configuramos esto como lo hicimos para el modelo lineal, pero usando el modelo logístico.
Luego usamos Solver para minimizar la celda E12, cambiando las celdas B1:B3. Nuestra solución indica que Capacidad=14996, C=99.93, y tasa=0.200.

Fortalezas y debilidades de los tres métodos de ajuste de curvas:
Hemos examinado tres métodos para encontrar una curva de mejor ajuste. Del capítulo 1, revisamos el método de trazar puntos y agregar una línea de tendencia. Usando la suma de la definición de error mínimo cuadrado de mejor ajuste, analizamos la creación de una función de error y el uso de Solver para minimizar el error. También analizamos el uso de derivadas parciales para encontrar puntos críticos de la función de error. Vale la pena mirar algunas de las fortalezas y debilidades de cada método.
El método de graficar puntos y usar el comando trendline tiene la ventaja de ser el método más simple cuando funciona. La mayor desventaja de este método es que sólo funciona con una pequeña colección de modelos matemáticos. (Podemos utilizar este método si nuestra ecuación deseada es lineal,\(y=mx+b\text{,}\) logarítmica,\(y=a \log(x)+b\text{,}\) polinomio de grado no superior a 6, potencia,\(y=ax^b\text{,}\) o exponencial\(y=ae^{bx}\text{.}\)) Como hemos visto en esta sección, no es difícil encontrar situaciones en las que deba usarse algún otro modelo. Este método también tiene la desventaja de simplemente dar una respuesta sin mostrar pasos intermedios que podrían proporcionar otra información útil.
El método de uso de derivados parciales tiene la ventaja de ser matemáticamente claro. Nos muestra lo que sucede cuando encontramos una curva de mejor ajuste. Sin embargo, en todos los casos menos en los más simples, este método tiene la desventaja de involucrar una desalentadora avalada de cálculos. Este método es bueno para informarnos sobre cómo funciona el método, pero no un método que queremos usar en la práctica para los problemas más realistas.
El método medio, usando Solver es un híbrido de los otros dos métodos. Comenzamos por decidir sobre el modelo matemático que debe ajustarse a nuestra situación. Como vimos, el método es sencillo para adaptarse a cualquier tipo de ecuación. Es sencillo construir explícitamente nuestra función de error. Este método también tiene la ventaja de hacer visible el error atribuido a cada punto. Podemos ver si otra curva es casi tan buena como la solución que encontramos.
Las desventajas del método Solver son las desventajas estándar de usar Solver para encontrar un mínimo. Recordemos que Solver simplemente encuentra un mínimo local desde un punto de partida. Dado que solver utiliza métodos numéricos busca lugares donde las derivadas parciales se encuentran dentro de nuestros límites de tolerancia de cero. No podemos esperar que Solver dé una respuesta más precisa que los límites de tolerancia. Con todos los métodos debemos ser conscientes de que necesitamos suficientes puntos para obtener un ajuste razonable de la curva. Intuitivamente un pequeño cambio en cualquier punto no debería provocar un gran cambio en la curva.
Como regla general, usaremos el comando trendline cuando funcione con el tipo de ecuación que hemos decidido usar como nuestro modelo.
clase=”Ejercicios: Optimización y problemas de curvas de mejor ajuste
Para los ejercicios 1-4, para los conjuntos de datos dados:
- Trace los puntos y agregue una línea de tendencia lineal. Mostrar la ecuación de la línea.
- Cree una hoja de cálculo para comparar los datos con una función lineal.
- Agrega error a tu hoja de cálculo. Encuentra la mejor línea de ajuste, usando Solver.
- Buscar explícitamente la suma de errores cuadrados funcionan como una función cuadrática de la pendiente m, y la intercepción b.
- Encuentra los valores de m y b que minimizan la función de error tomando derivadas parciales y poniéndolas iguales a 0.
Los puntos dados son:
| x | -2 | 0 | 6 |
| y | -7 | 5 | 15 |
- Contestar
-
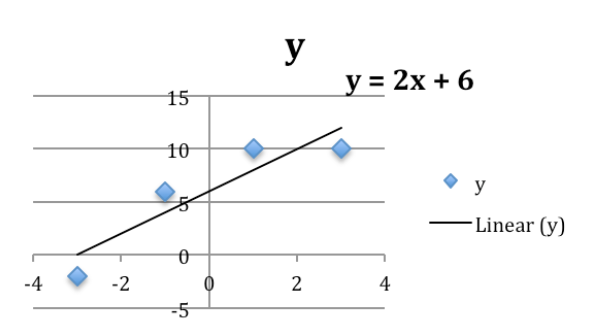
Con líneas de tendencia conseguimos la mejor línea de ajuste:
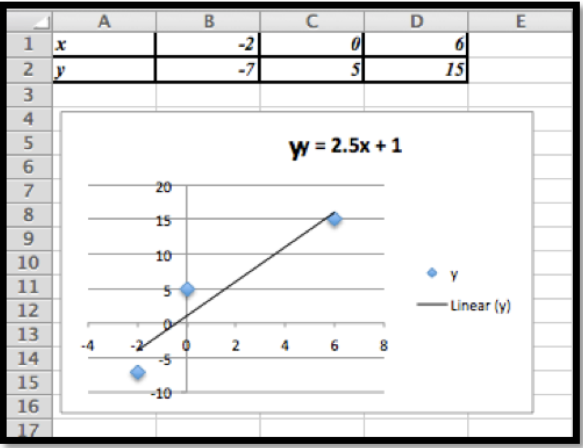

La línea que nos da la mejor curva de ajuste es\(y=2.5 x+1\text{.}\)
Usando el método de error de mínimos cuadrados tenemos los siguientes valores.
Podemos configurar la información como filas o como columnas. Usando las filas forman el problema inicial que tenemos

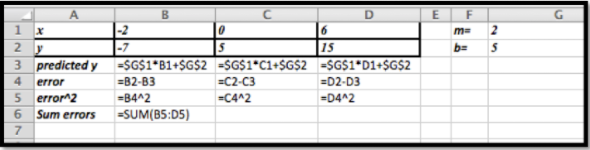
A continuación usamos Solver para minimizar la suma de los errores

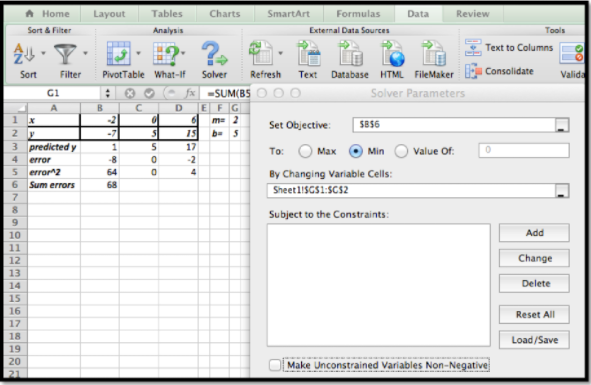
Empezamos con\(m=2\) y\(b=5\) (opciones algo arbitrarias)
Desmarcamos la restricción de que las variables deben ser no negativas (\(m\)y/o teóricamente\(b\) podrían ser negativas)

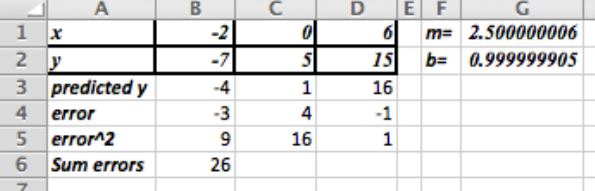
El método de mínimos cuadrados nos da la función\(y=2.5x+1\)
(Comentario: esto muestra que el método de mínimos cuadrados da la misma respuesta que el método de línea de tendencia. Sin embargo, el método de los mínimos cuadrados es una técnica más general y se puede utilizar en los casos en que las líneas de tendencia no sean suficientes).
Los puntos dados son:
| x | -2 | 0 | 6 |
| y | 24 | 10 | 20 |
Los puntos dados son:
| x | -3 | -1 | 1 | 3 |
| y | -2 | 6 | 10 | 10 |
- Contestar
-

Definiríamos\(m\)\(b\) y usaríamos estos para crear
\[ predicted\ y=mx+b \nonumber \]
Si no hubiéramos hecho la línea de tendencia, la pregunta sería: ¿para qué deberían los valores iniciales\(m\) y
Los datos van desde\((-3,-2)\) lo\((3,10)\) que sugiere una pendiente de\(m\approx (10-(-2))/(3-(-3) )=12/6=2\text{.}\)
Mirar los datos cerca del\(y\) eje sugiere una suposición inicial de\(b\approx 7.5\text{.}\)
Entonces empezaríamos con una hoja de Excel como esta:

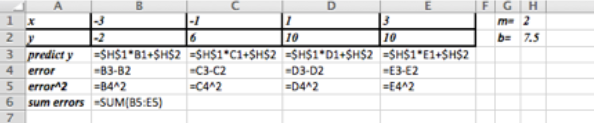

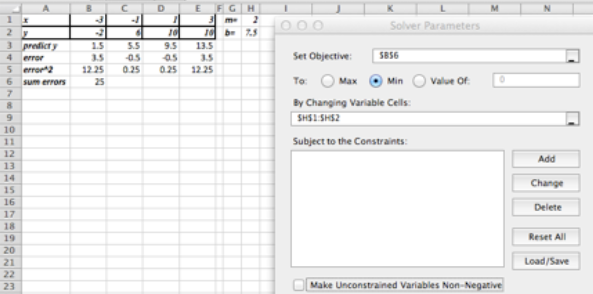
Configurando Solver como se muestra arriba obtenemos\(m = 2\) y\(b = 6\text{.}\)
Los puntos dados son:
| x | -2 | 0 | 2 | 4 |
| y | -7 | 5 | 11 | 11 |
Para los ejercicios 5-8, encuentra la curva del tipo indicado que da el mejor ajuste para los datos.
Sally tiene dinero invertido en una sola cuenta que agrava el retorno a la cuenta. Así, el modelo que queremos utilizar para la cantidad es:
\[ Amount(time)=InitialAmount* rate^{time} \nonumber \]
Con los datos:
| Tiempo | 0 | 2 | 5 | 10 | 15 | 20 |
| Monto | $5000 | $5600 | $6700 | $9000 | $12000 | $16000 |
Encuentre la mejor curva de ajuste del modelo dado.
- Contestar
-
Un diagrama de dispersión de los datos nos ayudará a encontrar algunas buenas conjeturas iniciales para la cantidad inicial y la tasa.

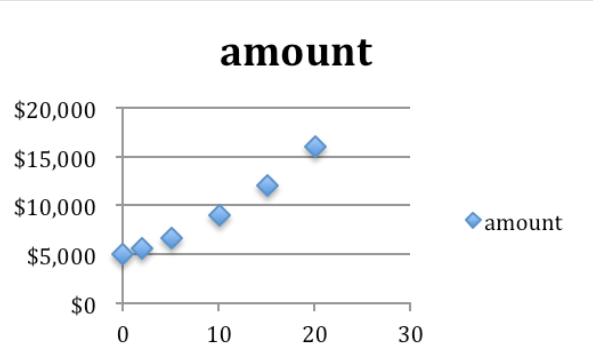
El\(y\) -intercepto es de alrededor de $5000. Esto ocurre cuando tiempo = 0, por lo que la suposición inicial para la cantidad inicial será de 5,000. El gráfico es una función creciente, por lo que sabemos tasa\(\gt 1\text{.}\)
Elegir tasa = 1 causará problemas (la base de una función exponencial no debe ser 1). Asumiendo que este es un problema de inversión razonable asumiremos un crecimiento de 5$, entonces\(r = 1.05\)
La configuración inicial se ve así. Hemos incluido una gráfica de los datos dados frente a los números pronosticados. Las conjeturas iniciales no son malas, pero claramente podemos hacerlo mejor.

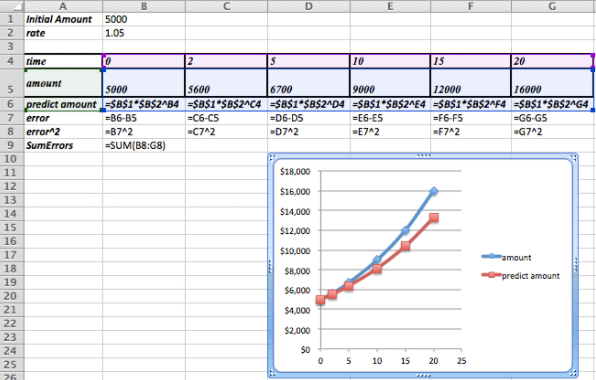
Después de usar Solver determinamos que la mejor función de modelo para nuestros datos es la siguiente:

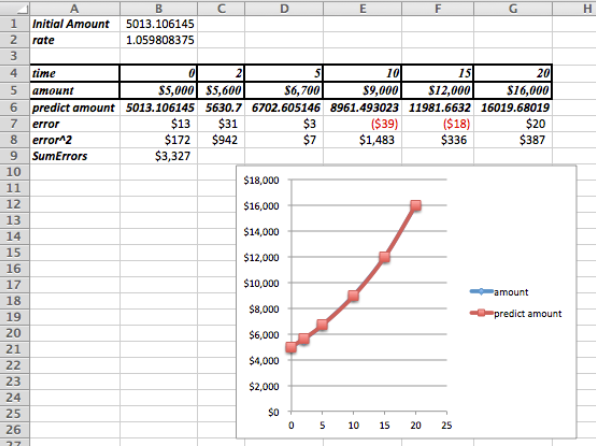
\[ Amount(time)=5,013.11* (1.06)^{time} \nonumber \]
Observe que los datos ahora son indistinguibles de la función de modelo en la gráfica.
Observación: Si usamos Trendlines para encontrar una función exponencial que se ajuste a los datos, obtendríamos\(y=5001 e^{0.0583*time}\)
El análisis de errores mínimos cuadrados muestra que esta no es una aproximación tan buena como la que acabamos de encontrar usando Solver! El error de mínimos cuadrados para la línea de tendencia es aproximadamente 30% mayor que para el valor que encontramos usando Solver.
Fred ha puesto parte de su dinero en una cuenta de efectivo que no paga intereses y el resto de su dinero una sola cuenta que agrava el retorno de vuelta a la cuenta. Así, el modelo que queremos utilizar para la cantidad es
\[ Amount(time)=CashAmount+InvestmentAmount*rate^{time} \nonumber \]
Con los datos:
| Tiempo | 0 | 2 | 5 | 10 | 15 | 20 |
| Monto | $10000 | $11000 | $14000 | $19000 | $27000 | $39000 |
Encuentre la mejor curva de ajuste del modelo dado.
Mary ha puesto parte de su dinero en una inversión que paga simple y el resto de su dinero en una sola cuenta que agrava el retorno de vuelta a la cuenta. Así, el modelo que queremos utilizar para la cantidad es
\[ Amount(time)=Amount1+Return1*time+Amount2*rate2^{time} \nonumber \]
Con los datos:
| Tiempo | 0 | 2 | 5 | 10 | 15 | 20 | 30 | 40 |
| Monto | $10000 | $11300 | $13500 | $18300 | $24700 | $33500 | $62600 | $118800 |
Encuentre la mejor curva de ajuste del modelo dado.
- Contestar
-
La función que estamos buscando tiene un componente lineal (amount1+return1*time), y un componente exponencial. No hay una línea de tendencia que haga esto por nosotros.
¿Qué sabemos de estos valores?
- Tenemos $10,000 al principio y esto se divide en dos inversiones diferentes, por lo que Monto 1 + Monto 2 = $10,000.
- ¿Qué es Return 1? Debe ser el retorno de la primera parte de la inversión. Entonces debería ser alguna cantidad que recibamos en una inversión de como máximo 10,000 dólares. Una primera conjetura sería que el valor está en los cientos de dólares, pero ¿tal vez cerca de $150 o $200?
- La tasa es nuestro parámetro final. Este es el crecimiento debido a los intereses. Empezaremos con una conjetura de\(rate = 1.05\text{.}\)
Los comandos de Excel utilizados para generar la tabla son los siguientes:

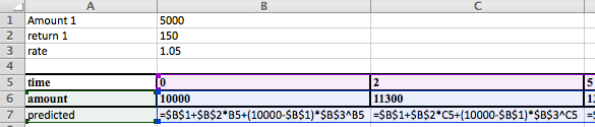
Vale la pena graficar tanto los datos reales como los datos predichos para ver si estamos configurando el problema correctamente.

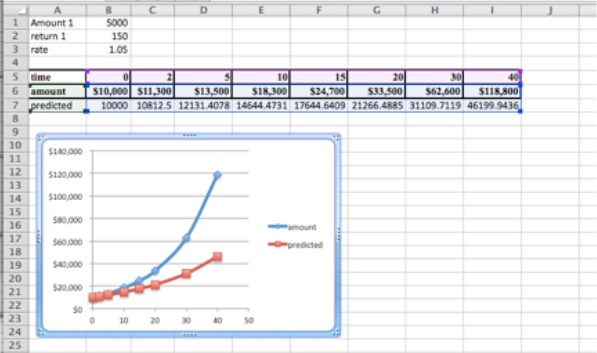
La forma general de la gráfica de valores predichos parece estar bien. Los valores están apagados, pero Solver podrá reducir el error.

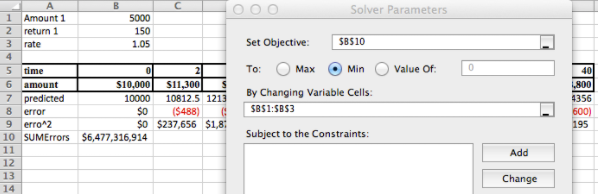
La solución es:
Monto 1 3317.59 retorno 1 163.19 tasa 1.07 De ahí\(Amount 2 = 10,000 – 3,317.59 = 6,682.41\text{,}\) y tenemos que
\[ Amount(time)=\$3,317.59+\$163.19*time+\$6,682.41* (1.07)^{time} \nonumber \]
En Excel los datos y los valores predichos ahora se alinean muy bien.
John ha dividido su dinero entre dos cuentas. Ambos agravan sus rendimientos, pero pagan tarifas diferentes. Así, la fórmula que modela la inversión es:
\[ Amount(time)=Amount1*rate1^{time}+Amount2*rate2^{time} \nonumber \]
Con los datos:
| Tiempo | 0 | 2 | 5 | 10 | 15 | 20 | 30 | 40 |
| Monto | $10000 | $11500 | $14000 | $20000 | $29000 | $41500 | $87000 | $183500 |
Encuentre la mejor curva de ajuste del modelo dado.


