7.3: Antidiferenciación básica
- Page ID
- 115980
En la última sección nos fijamos en el teorema fundamental del cálculo y vimos que se podía utilizar para encontrar integrales definidas. Vimos
Teorema Fundamental del Cálculo (segunda versión) Dejar\(f(x)\) ser una función continua en el intervalo\([a, b]\text{.}\) Supongamos que\(F(x)\) es cualquier función continua, diferenciable con\(\frac{d}{dx} F(x)=f(x)\text{.}\) Entonces\(\int_a^b f(t)\ dt=F(b)-F(a)\text{.}\)
Por lo tanto, nos parece muy útil poder encontrar sistemáticamente un antiderivado de una función. La notación estándar es usar un signo integral sin los límites de integración para denotar el anti-derivado general. Por lo tanto,\(\int_a^b f(t)dt\) se conoce como la integral definitiva\(f(x)\) de de\(a\) a\(b\text{,}\) y es un número. En contraste,\(\int f(x) dx\) es la integral indefinida de\(f(x)\) y es una función. Utilizamos integrales indefinidas o antiderivados para evaluar integrales o áreas definidas.
Encontramos anti-derivados comenzando con las fórmulas de diferenciación de funciones básicas y manipulándolas para que la derivada sea una función agradable
Elemental Anti-derivado 1 — Encuentra una fórmula para\(\int x^n\ dx\text{.}\) Empezamos con la fórmula de diferenciación más cercana\(\frac{d}{dx} x^n=nx^{n-1}\text{,}\) y la manipulamos así\(x^n\) está en el lado derecho. Primero\(n\) reemplazamos por\(n+1\) para obtener\(\frac{d}{dx} x^{n+1}=(n+1)x^n\text{.}\) Luego dividimos ambos lados por\(n+1\) para obtener\(x^n=\frac{d}{dx} x^{n+1}/(n+1)\text{.}\) Finalmente, observamos que agregar una constante\(C\) no cambia la derivada, entonces\(x^n=\frac{d}{dx} (x^{n+1}/(n+1)+C)\text{.}\) ya que hemos dividido por\(n+1\text{,}\) tenemos que insistir en que\(n+1\ne 0\text{.}\) Usando el notación de integrales indefinidas obtenemos nuestra fórmula de regla de poder:
\[ \int x^n\ dx=\frac{x^{n+1}}{n+1}+C, \hbox{assuming }n\ne -1. \nonumber \]
Tenga en cuenta que esto coincide con el patrón que encontramos en la última sección.
Elemental Anti-derivado 2 — Encuentra una fórmula para\(\int 1/x \ dx\text{.}\) Comenzamos con la fórmula de diferenciación más cercana\(\frac{d}{dx} \ln (x)=1/x\text{.}\) En este caso debemos tener en cuenta que los logaritmos naturales solo se definen números positivos y nos gustaría una fórmula que sea verdadera para números positivos y negativos. Podemos hacer esto con un uso apropiado de barras de valor absoluto. Así\(\frac{d}{dx} (\ln(|x|)+C)=1/x\text{,}\) y tenemos nuestra segunda fórmula:
\[ \int 1/x\ dx=\ln |x|+C. \nonumber \]
Elemental Anti-derivado 3 — Encuentra una fórmula para\(\int e^x\ dx\text{.}\) Una vez más, comenzamos con la fórmula de diferenciación más cercana\(\frac{d}{dx} e^x=e^x\text{.}\) En este caso no tenemos que hacer ninguna manipulación, y tenemos nuestra fórmula:
\[ \int e^x \ dx=e^x+C. \nonumber \]
Elemental Anti-derivado 4 — Encuentra una fórmula\(\int a^x\ dx\) para un número positivo a Esta fórmula requiere un poco más de trabajo. Comenzamos con la fórmula\(\frac{d}{dx} a^x=\ln (a) a^x\text{.}\) Dividiendo ambos lados por la constante ln (a) da\(a^x=\frac{d}{dx} (a^x/\ln (a) +C)\) Así nuestra integral es:
\[ \int a^x dx=\frac{a^x}{\ln (a)} +C. \nonumber \]
Reglas Suma, Diferencia y Múltiple Constante — Las reglas que teníamos para tomar derivadas de sumas, diferencias y múltiplos constantes de funciones se traducen en reglas similares para integrales.
Las derivadas de una regla de suma,\(\frac{d}{dx}(f(x)+g(x))=\frac{d}{dx}f(x)+\frac{d}{dx}g(x) \text{,}\) se convierte en
Integral de una Regla de Suma:
\[ \int (f(x)+g(x))\ dx=\int f(x)\ dx+\int g(x)\ dx \nonumber \]
Los derivados de una regla de diferencia,\(\frac{d}{dx}(f(x)-g(x))=\frac{d}{dx}f(x)-\frac{d}{dx}g(x) \text{,}\) se convierte en el
Integral de una Regla de Diferencia:
\[ \int (f(x)-g(x))\ dx=\int f(x)\ dx-\int g(x)\ dx \nonumber \]
Integral de una Regla Múltiple Constante:
\[ \int cf(x) dx=c\int f(x)\ dx \nonumber \]
Podemos usar estas reglas para encontrar las integrales indefinidas en muchas funciones. Cubren todos los polinomios.
Encuentra la integral\(\int 3x^5+4x^2+5+\frac{7}{x}\ dx\text{.}\)
Solución
\[ \int 3x^5+4x^2+5+\frac{7}{x}\ dx \nonumber \]
\[ =\int 3x^5\ dx+\int 4x^2\ dx+\int 5\ dx+\int \frac{7}{x}\ dx\qquad\hbox{(sum rule)} \nonumber \]
\[ =3\int x^5\ dx+4\int x^2\ dx+5\int \ dx+\int 7\frac{1}{x}\ dx\qquad\hbox{(constant multiple rule)} \nonumber \]
\[ =3\int x^5\ dx+4\int x^2\ dx+5\int \ dx+ 7\ln|x|+C\qquad\hbox{(natural log rule)} \nonumber \]
\[ =\frac{3}{6} x^6+\frac{4}{3}x^3+5x+ 7\ln|x|+C\qquad\hbox{(power rule)} \nonumber \]
Se podría argumentar que la última línea debería haber sido
\[ =\frac{3}{6} x^6+C_1+\frac{4}{3}x^3+C_2+5x+C_3+ 7\ln|x|+C_4 \nonumber \]
ya que cada integral indefinida obtiene una constante C. Sin embargo, todas las\(C_i\) que se usan aquí son constantes arbitrarias y pueden colapsarse juntas en una sola constante C.
También podemos usar estas reglas para encontrar integrales indefinidas para raíces.
Encuentra la integral\(\int \sqrt{2x}+\sqrt[3]{4x}\ dx\text{.}\)
Solución
\[ \int \sqrt{2x}+\sqrt[3]{4x}\ dx =\int \sqrt{2x}\ dx+\int \sqrt[3]{4x}\ dx\qquad\hbox{(sum rule)} \nonumber \]
\[ =\sqrt{2}\int \sqrt{x}\ dx+\sqrt[3]{4}\int \sqrt[3]{x}\ dx \qquad\hbox{(constant multiple rule)} \nonumber \]
\[ =\sqrt{2}\int x^{(1/2)}\ dx+\sqrt[3]{4}\int x^{(1/3)}\ dx\qquad\hbox{(rules of exponents)} \nonumber \]
\[ =\sqrt{2} x^{(3/2)}(2/3)+\sqrt[3]{4}x^{(4/3)}(3/4)+C\qquad\hbox{(power rule)} \nonumber \]
También podemos encontrar anti-derivados de funciones exponenciales y de potencia.
Encuentra la integral\(\int 2*3^x+4e^x\ dx\text{.}\)
Solución
\[ \int 2*3^x+4e^x\ dx=\int 2*3^x\ dx+\int 4e^x\ dx\qquad\hbox{(sum rule)} \nonumber \]
\[ =2\int 3^x\ dx+4\int e^x\ dx\qquad\hbox{(constant multiple rule)} \nonumber \]
\[ =\frac{2}{\ln(3)} 3^x+4 e^x+C\qquad\hbox{(exponential rules)} \nonumber \]
Como mencionamos anteriormente en la sección, la razón normal para querer encontrar integrales indefinidas es poder utilizarlas con el teorema fundamental del cálculo para encontrar integrales definidas.
Evaluar la integral definida\(\int_1^3 6x^2+2\ dx\text{.}\)
Solución
Primero evaluamos la integral indefinida para encontrar un anti-derivado.
\[ \int 6x^2+2\ dx=2x^3+2x+C. \nonumber \]
Como podemos usar cualquier anti-derivado, simplificamos fijando\(C = 0\) y eligiendo el anti-derivado\(F(x)=2x^3+2x\text{.}\)
\[ \int_1^3 6x^2+2\ dx=F(3)-F(1)=60-4=56. \nonumber \]
Evaluar la integral definida\(\int_1^{100}\frac{1}{x} dx\text{.}\)
Solución
Primero evaluamos la integral indefinida para encontrar un antiderivado.
\[ \int \frac{1}{x}\ dx=\ln(|x|)+C \nonumber \]
Como podemos usar cualquier antiderivado, simplificamos configurando\(C = 0\) y eligiendo ese anti-derivado\(F(x)=\ln(|x|)\text{.}\)
\[ \int_1^{100}\frac{1}{x}\ dx=F(100)-F(1)=\ln(100)-\ln(1)=\ln(100). \nonumber \]
Por experiencia, sé que la salida de un pozo petrolero sigue un modelo de decaimiento exponencial. Tengo los siguientes datos para la producción, en barriles, para los primeros 5 meses.
| Mes | Ene | Feb | Mar | Abr | Mayo |
| Producción | 1000 | 971 | 925 | 887 | 859 |
Encuentra la producción durante los primeros 5 años.
Solución
La producción total por 5 años será la integral definitiva de la función de producción durante los primeros 60 meses. Primero usamos Excel para encontrar una función exponencial que mejor se ajuste.

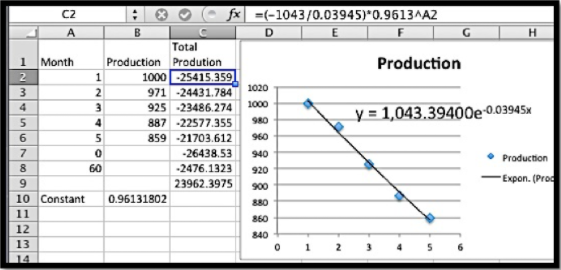
La función de producción (P) en términos del número de meses (x) viene dada por
\[ P(x)=1043 e^{-0.03945 x} \nonumber \]
Nos gustaría tomar un anti-derivado, pero aún no tenemos una fórmula para este antiderivado. Sin embargo, observamos
\[ e^{-0.03945 x}= (e^{-0.03945} )^x=0.9613^x \nonumber \]
y sabemos que ahora\(\ln (0.9613)=-0.03945\text{.}\) podemos usar nuestra regla exponencial, y
\[ AntiderivP(x)=\frac{(1043*0.9613^x)}{(-0.03945)}+C \nonumber \]
Ya que podemos usar cualquier anti-derivado,\(C = 0\text{.}\) simplificamos configurando Podemos hacer esto sin crear ningún problema porque estamos usando la ecuación donde dos valores de la anti-derivada se restarán uno del otro, y de ahí los valores C cancelarían de todos modos. Ahora evaluamos nuestra integral.
\[ TotalP(60)= ArtiderivP(60)– AntiderivP(0) \nonumber \]
\[ = (-2467) – (-26438) = 23962 \nonumber \]
Así, a lo largo de 5 años el pozo producirá 23,962 barriles.
Otra aplicación para los antiderivados es resolver un problema de valor inicial. En ese caso queremos un anti-derivado particular que tenga un valor particular para una x especificada. En esta situación no podemos establecer C en cero. De hecho, parte del problema será encontrar el valor apropiado de C.
El costo marginal (MC) de producir una cierta cantidad (q) de widgets viene dado por
\[ MC(q)=5-0.002 q \nonumber \]
El costo de producir 1000 widgets es de $6,000. Supongamos que la derivada de la función de costo se aproxima lo suficientemente cerca por el costo marginal para ser utilizada indistintamente. Encuentre una función de costo para producir widgets.
Solución
Dado que el Costo es un antiderivado del Costo Marginal tenemos\(Cost(q) = 5q - 0.001*q^2 + C\)
También sabemos\(Cost(1000) = 6000\text{.}\) Plugging que en da
\[ Cost(1000)= 5*1000 - 0.001*1000^2 + C=6000 \nonumber \]
Resolviendo para C da\(C = 2000\text{.}\) Así nuestra función de costo es
\[ Cost(q) = 5q - 0.001*q^2 + 2000 \nonumber \]
La experiencia me dice que el beneficio marginal de producir gadgets es una función lineal. Mis costos iniciales son de 2 millones de dólares. Tengo los siguientes datos siendo mis unidades miles de dólares por millones de unidades.
| Producción | 0 | 1 | 2 | 3 | 4 |
| Beneficio marginal | 3,3967 | $3,603 | $3,236 | $2,795 | $2,384 |
Producir una función de ganancia, encontrar el número de unidades que maximiza el beneficio y encuentra el beneficio máximo
Solución
Empiezo por encontrar una línea de mejor ajuste a los datos.

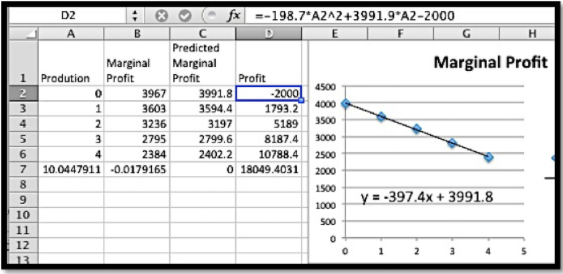
Excel me dice que la función de beneficio marginal es
\[ MP(x) = -397.4 x + 3991.8 \nonumber \]
Tenemos el máximo beneficio cuando el beneficio marginal es cero. Usando Goal Seek, el Beneficio Marginal es cero con una producción de 10.0448 millones de unidades. El anti-derivado de esta función es
\[ P(x)= -198.7 x^2 + 3991.8x + C \nonumber \]
Conectando los costos iniciales al modelo de producción, recordando que nuestra función está escrita en miles de dólares por millón de widgets, da
\[ P(0) = -2000 = C \nonumber \]
Entonces nuestra función de ganancia es
\[ P(x)= -198.7 x^2 + 3991.8 x-2000 \nonumber \]
Vimos que\(MP(x) = 0\text{,}\) cuando\(x = 10.0448\text{.}\) La ganancia máxima es la calculada evaluando\(P(x)\) en\(x = 10.0448\text{.}\) Un cálculo rápido muestra que la ganancia máxima es de $18,049 miles de dólares, o un poco más de 18 millones de dólares.
Vale la pena resumir nuestra lista de fórmulas de integración.
| \(f(x)\) | \(\int f(x)\ dx\) |
| \(\displaystyle x^n\hbox{, assuming }n\ne 1\) | \(\displaystyle \frac{x^{n+1}}{n+1}+C\) |
| \(\displaystyle \frac{1}{x}\) | \(\displaystyle \ln|x|+C\) |
| \(\displaystyle e^x\) | \(\displaystyle e^x+C\) |
| \(\displaystyle a^x\) | \(\displaystyle \frac{a^x}{\ln(a)}+C\) |
| \(\displaystyle (f+g)(x)\) | \(\displaystyle \int f(x)dx+\int g(x)dx\) |
| \(\displaystyle (f-g)(x)\) | \(\displaystyle \int f(x)dx-\int g(x)dx\) |
| \(\displaystyle c*f(x)\) | \(\displaystyle c*\int f(x)dx\) |
Una advertencia — Las fórmulas antidiferenciación que hemos producido sólo funcionan para las funciones dadas, permitiendo cambios en las variables. En este punto la única manera que tenemos para encontrar\(\int(3x+5)^2 dx\) es ampliar el integrand consiguiendo\(\int(9x^2+30x+25)dx\) antes de aplicar nuestras reglas. En general el proceso de encontrar simbólicamente antiderivados es una forma de arte con la que solo comenzamos a trabajar en este curso.
clase=”Ejercicios: Problemas Básicos de Antidiferenciación
Encuentra antiderivados para las funciones dadas.
\[ f(x)=3x+5. \nonumber \]
- Contestar
-
\[ F(x)=\frac{3x^2}{2}+5x+Constant \nonumber \]
\[ f(x)=5x^3+4x+3. \nonumber \]
\[ f(x)=x^{3,124,567}+2x^{473}+327 x^{-2,786,534}. \nonumber \]
- Contestar
-
\[ F(x)=\frac{x^{3,124,568}}{3,124,568}+2 \frac{x^{474}}{474}+327 \frac{x^{-2,786,533}}{-2,786,533}+Constant \nonumber \]
\[ f(x)=\sqrt{11x}+\frac{5}{x}. \nonumber \]
\[ f(x)=e^x+\left(\frac{1}{2}\right)^x. \nonumber \]
- Contestar
-
\[ F(x)=e^x+\frac{\left(\frac{1}{2}\right)^x}{\ln\left(\frac{1}{2}\right)}+Constant \nonumber \]
\(f(x)=\pi^x+\pi^\pi+x^\pi.\)
Evaluar las integrales definidas encontrando primero un antiderivado.
\[ \int_0^5 x+7\ dx \nonumber \]
- Contestar
-
\[ \int_0^5 (x+7)dx=F(5)- F(0)=\frac{25}{2}+35-0=\frac{95}{2} \nonumber \]
\[ \int_1^{10}\frac{1}{x}\ dx \nonumber \]
\[ \int_2^{10} 3x+\frac{5}{x}\ dx \nonumber \]
- Contestar
-
El anti-derivado es:\(F(x)=(3x^2)/2+5 \ln|x|\)
\[ \int_2^{10} 3x+\frac{5}{x} dx =F(10)-F(2) =\frac{300}{2}+5 \ln(10)-\left(\frac{12}{2}+5 \ln(2) \right) \nonumber \]
\[ =150+5 \ln(10)-6-5 \ln(2)=144+5(\ln(10)-\ln(2) ) \nonumber \]
\[ = 144+5 \ln\left(\frac{10}{2}\right)=144+5 \ln(5) \nonumber \]
\[ \int_1^{100}\left(\frac{1}{2}\right)^x\ dx. \nonumber \]
\[ \int_{-10}^2 e^x+e \ dx \nonumber \]
- Contestar
-
El anti-derivado es:\(F(x)=e^x+e x\)
\[ \int_{-10}^2 e^x+e dx =F(2)-F(-10)=e^2+2e-(e^{-10}-10 e) \nonumber \]
\[ = e^2-\frac{1}{e^{10}} -8 e \nonumber \]
\[ \int_{-2}^5 x^{-2}+x^{-1} \ dx \nonumber \]
Resolver el problema del valor inicial.
Let\(f(x)=4x+3\text{.}\) La función\(F(x)\) es un antiderivado, y\(F(0)=7\text{.}\)
- Contestar
-
El anti-derivado es:\(F(x)=2x^2+3x+C\text{.}\)
\(F(0)= 7\)implica\(F(0)=0+C=7\text{,}\) que\(C = 7\)
Entonces\(F(x)=2x^2+3x+7\text{.}\)
Let\(f(x)=3x^2-6x+5\text{.}\) La función\(F(x)\) es un antiderivado, y\(F(3)=17\text{.}\)
Let\(f(x)=100(0.95)^x\text{.}\) La función\(F(x)\) es un antiderivado, y\(F(5)=9\text{.}\)
- Contestar
-
El anti-derivado es:
\[ F(x)=\frac{100 (0.95)^x }{\ln(0.95)} +C \nonumber \]
\(F(5)= 9\)implica que
\[ F(5)=\frac{100 (0.95^5 )}{\ln(0.95)} +C=9 \nonumber \]
\[ C=9-\frac{100 (0.95^5 )}{\ln(0.95)}\approx 9+1508.54=1517.54 \nonumber \]
Entonces
\[ F(x)\approx\frac{100 (0.95^x )}{\ln(0.95)} +1517.54 \nonumber \]
Let\(f(x)=7/x+x^2\text{.}\) La función\(F(x)\) es un antiderivado, y\(F(1)=11\text{.}\)
Una inversión proporciona un flujo de ingresos de\(1000 (0.95)^t\) dólares por año. ¿Cuánto se recibe en los primeros 10 años?
- Contestar
-
\[ Income=\int_0^{10}1000(0.95)^t dt =\left.\frac{1000(0.95)^t)}{\ln(0.95)} \right|_{t=0}^{t=10} \nonumber \]
\[ =\frac{1000(0.95)^{10}}{\ln(0.95)} -\frac{1000(0.95)^0)}{\ln(0.95)} \nonumber \]
\[ \approx -11672.81+19495.73=7822.91 \nonumber \]
Una firma tiene una función de ganancia marginal\(MP(x) = 50 – 3 x\) de miles de dólares por miles de unidades. ¿Cuánto se incrementa el beneficio si la producción se desplaza de 10 a 15 mil unidades?
Después del primer año, la tasa de ventas de un producto de moda son\(sales(t) = \frac{1000}{t}\) con el tiempo en años. ¿Cuántas unidades se venden desde el final del primer año hasta el final del décimo año?
- Contestar
-
\[ sales=\int_1^{10}\frac{1000}{t} dt=1000 \ln(t) |_{t=1}^{t=10} \nonumber \]
\[ =1000(\ln(10)-\ln(0) ) \nonumber \]
\[ =1000\ln(10)\approx 2302.58 \nonumber \]
Una empresa de software permite a su empresa ampliar el número de licencias que posee su empresa cobrando una tasa marginal de\(MR(licenses)=\frac{200}{\sqrt{licenses}}\text{.}\) ¿Cuánto cuesta aumentar su licencia de 1000 a 2000 licencias?
La función de producción para un pozo petrolero dado es\(rate(t) = 400(0.9)^t\) con el tiempo medido en años y la producción medida en millones de barriles de petróleo.
- ¿Cuánto aceite se produce en el primer año?
- ¿Cuánto petróleo se produce en el décimo año?
- Si necesito producir 75 mil barriles de petróleo al año para que el pozo sea financieramente viable, ¿cuál es la vida del pozo?
- ¿Cuánto petróleo producirá el pozo antes de ser cerrado?
- Contestar
-
- \[ Production=\int_0^{1}400(0.9)^t dt =\left.\frac{400}{\ln(0.9)} (0.9)^t \right|_{t=0}^{t=1} \nonumber \]


