7.6: La distribución normal- Un ejemplo numérico extendido

Última actualización
Guardar como PDF

Page ID: 115987

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Queremos mirar un ejemplo extendido donde de manera realista queremos encontrar una integral definida, pero necesitamos usar métodos numéricos en lugar de resolver para la antiderivada y usar el teorema fundamental del cálculo. La mayoría de los estudiantes están familiarizados con el concepto de un curso que se califica en una curva. Formalmente eso significa que hay una distribución preestablecida de las calificaciones disponibles en la clase, con un cierto porcentaje de los estudiantes obteniendo una A, un cierto porcentaje obteniendo una B, y así sucesivamente. La mayoría de los estudiantes universitarios también están familiarizados con las pruebas ACT, SAT u otras pruebas estandarizadas, donde las calificaciones suelen seguir una curva normal o de campana. El resultado que sacamos de las matemáticas más avanzadas es que muchos fenómenos como la altura, el peso y el tamaño del sombrero, también siguen una curva de campana. En un entorno de negocios, a menudo nos preocupa si una parte de un mercado será lo suficientemente grande como para soportar una tienda especializada. También queremos saber qué parte de mi producción debe destinarse a una gama de tamaños de un producto. Esta pregunta a menudo se reduce a encontrar el área bajo una porción específica de la curva normal.

Antecedentes de probabilidad

Queremos sacar algunas definiciones y resultados de la teoría de la probabilidad. En particular queremos una descripción de la función en la que estamos encontrando el área bajo y también de la función de área relacionada.

Definición: Función de densidad de probabilidad

Una Función de Densidad de Probabilidad es una función que extiende el área 1 sobre toda la línea real, con el entendimiento obvio de que ningún valor puede tener una probabilidad negativa.

En términos de cálculo, una Función de Densidad de Probabilidad es una función$f(x)$ definida para$-\infty\lt x \lt \infty $ tal que$f(x)\ge 0$ y$\int_{-\infty}^{\infty}f(x)dx=1\text{.}$

Una función de densidad de probabilidad también se denomina función de distribución continua. La función de densidad de probabilidad que más nos interesa es la distribución normal. La función de densidad normal viene dada por

\[ f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right) \nonumber \]

donde sigma$\sigma\text{,}$ y mu$\mu\text{,}$ son respectivamente la desviación estándar y la media de la distribución. Para este curso la media es el centro de la distribución y la desviación estándar es una medida de cuán apretada está la distribución. Si establecemos la media en 0 y la desviación estándar en 1 tenemos la distribución normal estandarizada, o la curva de campana familiar.

Así, cuando observo que los hombres adultos en Estados Unidos tienen una distribución de altura que es normal con una media de 70 pulgadas y una desviación estándar de 3 pulgadas, la distribución es

\[ f(x)=\frac{1}{3\sqrt{2\pi}}\exp\left(\frac{-(x-70)^2}{2*3^2}\right) \nonumber \]

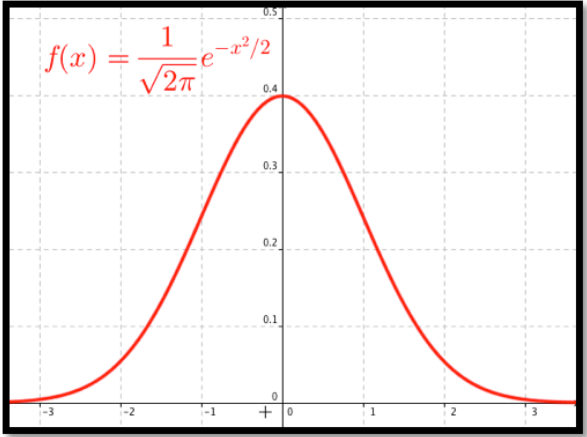
$clipboard_e27993c7294ca2e8be3f49d78e2876358.png$

De esta manera, encontrar el porcentaje de hombres menores de 5 pies de altura, se reduce a evaluar la integral adecuada. Dado que encontrar el porcentaje de la población que cabe en nuestro mercado se reduce a encontrar el área bajo una porción específica de esta curva, también nos interesa el antiderivado de la distribución.

Definición: Función de distribución acumulativa

Dada una función de densidad de probabilidad$f(x)$, la función de distribución acumulativa relacionada,$CDFf(x)\text{,}$ es una función que mide cuánta área hay en el intervalo$(-\infty,x]\text{.}$

En términos de cálculo,$CDFf(x)\text{,}$ la función de distribución acumulativa de$f(x)\text{,}$ es$\int_{-\infty}^x f(t)dt\text{.}$

Notarás que las técnicas que tenemos para la antidiferenciación no funcionarán con la distribución normal. De hecho, la distribución normal no tiene forma cerrada anti-derivada utilizando las funciones con las que estamos familiarizados. Por lo tanto, necesitamos usar métodos numéricos.

Ejemplo 7.6.1: Hombres altos en una zona

En Estados Unidos, la estatura de los hombres sigue una distribución normal con una media de 70 pulgadas (5' 10") y una desviación estándar de 3 pulgadas. Quiero montar una tienda especializada para hombres que midan al menos 6' de altura, pero no más de 7' de estatura. En una zona con 100 mil hombres adultos, ¿qué tan grande es mi mercado potencial?

Configura la solución. Mi función de distribución es$\frac{1}{3\sqrt{2\pi}}\exp\left(\frac{-(x-70)^2}{2*3^3}\right)\text{.}$ Dado que tengo una población de 100,000 y estoy interesado en los hombres que miden entre 72 y 84 pulgadas de alto, mi mercado potencial es

\[ 100000\int_{72}^{84} \frac{1}{3\sqrt{2\pi}} \exp\left(\frac{-(x-70)^2}{2*3^2} \right)dx. \nonumber \]

Como alternativa, puedo convertir el problema por lo que se expresa en términos de desviaciones estándar. Luego utilizo la distribución normal estandarizada y mis límites de integración son

\[ low\ bound\ in\ SD = (low\ bound-mean)/(SD) = (72-70)/3 = 2/3 \nonumber \]

\[ upper\ bound\ in\ SD = (upper\ bound-mean)/(SD) = (84-70)/3 = 14/3. \nonumber \]

Entonces mi mercado potencial es

\[ 100000\int_{2/3}^{14/3} \frac{1}{\sqrt{2\pi}} \exp(-x^2/2)dx. \nonumber \]

Solución

1, usando Excel y Riemann Sumas: Quiero configurar una hoja de cálculo para encontrar el área bajo la curva. Como creo que puedo hacer esto por varios problemas, quiero configurar la hoja de trabajo como una plantilla que simplemente pueda rellenar. Me hará la vida más fácil si reformulo el problema en términos de desviaciones estándar. Mi mercado potencial es$100000\int_{2/3}^{14/3} \frac{1}{\sqrt{2\pi}} \exp(-x^2/2)dx\text{.}$ que estoy listo para configurar una hoja de trabajo de suma de Riemann como lo hicimos en la sección$7.1$

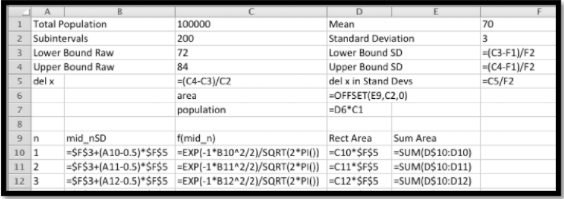
$clipboard_e7d9377e8119207b63c599ed2ba5a9edc.png$

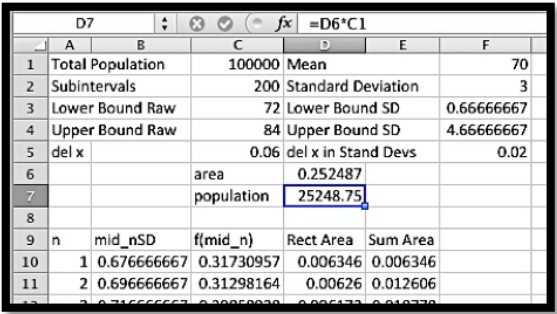
En las celdas F3 a F5 convertimos el límite inferior, el límite superior y del x en desviaciones estándar. Recordamos que obtenemos mejor precisión al evaluar los rectángulos con un punto medio. El punto medio del rectángulo enésimo es (n-0.5) *del x por encima del límite inferior. Como hicimos en secciones anteriores, utilizamos el comando offset para llevar nuestra respuesta a la región superior. Cuando miramos los números vemos que el mercado potencial es de 25,249.

$clipboard_e89fca458c3a48b34512396e6706eadb6.png$

Solución 1a, usando Comandos de Estadísticas de Excel: En este punto del curso debes esperar que si afirmamos que un cálculo es importante y hecho por negocios muchas veces, que haya un comando de Excel para hacer el cálculo.

La función que nos interesa es

\[ \hbox{NORM.DIST(x, mean, standard deviation, cumulative).} \nonumber \]

Donde$x\text{,}$ media, y desviación estándar tienen los significados obvios. El parámetro acumulativo es verdadero o falso. Si es cierto obtenemos la función de distribución acumulativa. Si es falso obtenemos la función de densidad de probabilidad. Si estamos trabajando con la distribución normal estandarizada, donde la media es 0 y la desviación estándar es 1, el comando es

\[ \hbox{NORM.S.DIST(x, cumulative).} \nonumber \]

(Si está utilizando versiones anteriores de Excel, la sintaxis del comando es un poco diferente. Consulte la página de ayuda correspondiente si está utilizando una versión anterior de Excel.) Con estos comandos, nuestra hoja de cálculo es notablemente más sencilla.

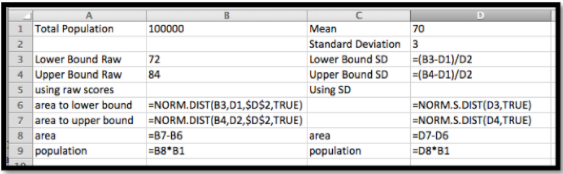
$clipboard_e270fec1cfe3ac8e8cf38aa5d0c0776d8.png$

Cuando miramos los valores, obtenemos una población objetivo de 25.249. Esto concuerda con nuestra estimación a 5 cifras significativas.

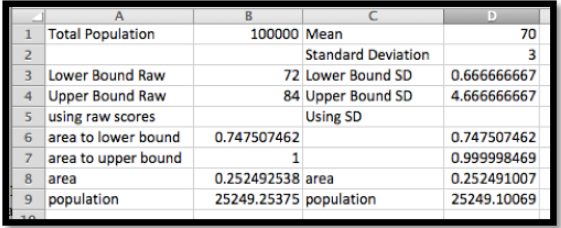
$clipboard_e2d57a1fb2553b171bb74d11688b47bfb.png$

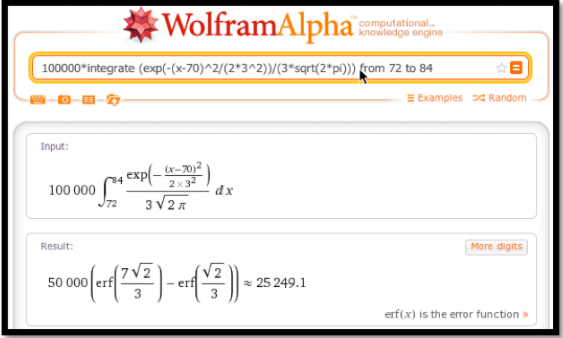
Solución 1b, usando Wolfram alpha: Una vez que he reducido el problema a evaluar una integral definida, puedo encontrar una solución numérica con un paquete CAS como Wolfram|Alpha.

\[ 100000\int_{72}^{84} \frac{1}{3\sqrt{2\pi}} \exp\left(\frac{-(x-70)^2}{2*3^2 }\right)dx \nonumber \]

se convierte

100000*integrar (exp (- (x-70) ^2/ (2*3^2))/(3*sqrt (2*pi))) de 72 a 84.

Obtenemos nuestra respuesta familiar de 25,249.

$clipboard_e37b8d70efd29bbe81f29f7f4653507ce.png$

Cuando calculamos una población objetivo, a veces queremos incluir la cola de la distribución. Podríamos, por ejemplo, preocuparnos por todas las mujeres que midan 5 pies de altura o menos. Esto configura una integral a lo largo de un intervalo infinito, lo que no podemos hacer como suma de Riemann. La primera solución señala que las colas son muy pequeñas. Si todos los humanos que alguna vez han vivido están normalmente distribuidos, menos de 1 es más de 7 desviaciones estándar de la media. Bajar la integral a -7 será prácticamente lo mismo que integrar hasta$-\infty\text{.}$ La segunda solución alternativa utiliza la simetría de la distribución normal.

\[ \int_{-\infty}^a SND(x)dx=\int_{-\infty}^0 SND(x)dx+\int_0^a SND(x)dx=.5+\int_0^a SND(x)dx. \nonumber \]

Ejemplo 7.6.2: Encontrar mujeres de baja estatura.

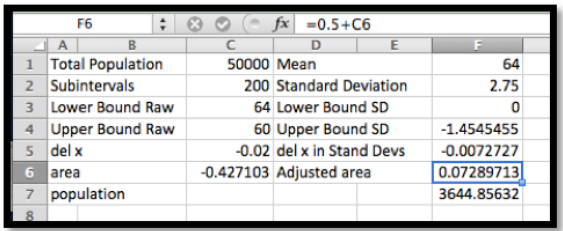
En Estados Unidos, la estatura de las mujeres sigue una distribución normal con una media de 64 pulgadas (5' 4") y una desviación estándar de 2.75 pulgadas. Quiero montar una tienda especializada para mujeres de no más de 5' de altura. En una zona con 500 mil mujeres adultas, ¿qué tan grande es mi mercado potencial?

Solución Configurar: Utilizando el razonamiento anterior, quiero estimar mi mercado si es 50% de la población más el porcentaje entre 0 y (-4/2.75) desviaciones estándar por debajo de la media.

Solución

Usando Excel y Riemann Sumas: Una ventaja de haber configurado bien el primer ejercicio, es que el problema de la suma de Riemann ahora es cuestión de cambiar los parámetros y restar de 0.5 antes de multiplicar por el tamaño del mercado.

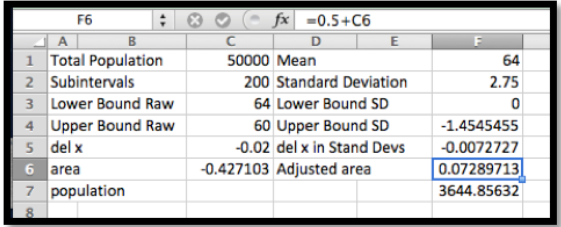
$clipboard_e35df68a17990359dbb63393d7e2b9cc9.png$

Observamos que ya que estamos encontrando el área bajo la distribución normal estandarizada de 0 a un número negativo, obtenemos un área negativa. Nuestro mercado potencial está compuesto por 3,645 mujeres.

Uso de comandos de estadísticas de Excel: Al usar los comandos de estadísticas, la función de área es cero en$-\infty\text{.}$ Así simplemente tenemos que evaluar

NORM.S.DIST (límite derecho, acumulativo).

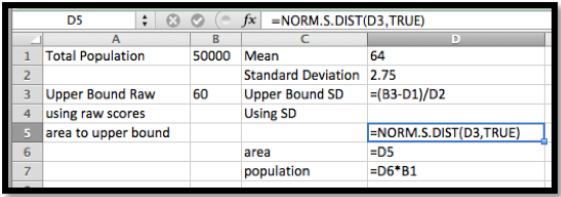
$clipboard_ec197e8d40cb302701c7a8f50c1a0d4ee.png$

Una vez más, conseguimos un mercado potencial de 3,645 mujeres.

Mientras que la distribución normal extiende una población sobre los números reales, la mayoría de los objetos vienen en tamaños discretos. Dependiendo del tipo de zapatos, las tallas son números enteros o medios. No se puede comprar un zapato de la talla 8.764. El procedimiento normal es dividir la población a la mitad entre los tamaños.

Ejemplo 7.6.3: Zapatos de Mujer.

En Estados Unidos, las tallas de zapatos de las mujeres siguen una distribución normal con una media de 8 y una desviación estándar de 1.5. Quiero pedir 1000 pares de zapatos. Si los zapatos solo están disponibles en tallas completas, ¿cuántos pares debo pedir de talla 7?

Solución

Quiero la porción de la población entre la talla 6.5 y 7.5. Lo meto en mi hoja de trabajo para sumas de Riemann.

$clipboard_e03b897f8cbc015de4a9f469cc174d1c6.png$

De los 1000 pares de zapatos, 211 deben ser la talla 7.

Hemos analizado tres métodos para encontrar una porción de una población normalmente distribuida, que describimos como Excel con sumas de Riemann, Excel con comandos estadísticos y CAS. Vale la pena considerar las ventajas y desventajas de los métodos. El método de sumas de Riemann toma más trabajo para configurar. También es conceptualmente el más directo y el más flexible. Es lo más fácil de adaptar si estamos haciendo alguna distribución no estándar de una población. También muestra valores intermedios si tenemos una pregunta menos aguda y estamos tratando de ver qué está pasando y todavía estamos decidiendo sobre la cuestión de negocios que queremos hacer. El enfoque de comandos de Excel con estadísticas requiere que aprendamos comandos especiales. También es menos trabajo. Probablemente sería el método favorecido si estuviéramos haciendo muchos de estos cálculos. Cabe señalar que Excel tiene los comandos correspondientes para las otras distribuciones de probabilidad estándar. El método CAS no requiere comandos especiales, pero nos saca de nuestro entorno Excel. No nos deja dejar una hoja de trabajo que esté bien documentada y que pueda ser fácilmente modificada por otra persona haciendo preguntas similares.

clase=”

Ejercicios: Problemas de distribución normal

Ejercicio 1:

Supongamos que las tallas de zapatos de mujer normalmente se distribuyen con una media de 8 y una desviación estándar de 1.5. Un estilo particular de zapatos disponible en tallas completas y medias. Planeo hacer 10 mil pares de este estilo.

Expresar, como integral, el número de pares que debo hacer de talla 9.
¿Cuántos pares de zapatos talla 9 debo hacer?
¿Cómo cambian tus respuestas si los zapatos solo se hacen en tallas completas?

Contestar

\[ \hbox{pairs size 9}=10000\int_{8.75}^{9.25} \frac{1}{1.5\sqrt{2\pi}}e^{\left({\frac{-(x-9)^2}{2*1.5^2}}\right)}\ dx \nonumber \]