4.12: Ejemplos Aplicados de Funciones
- Page ID
- 112558
Ejemplos aplicados de función (¡AKA word problems!) puede tomar muchas formas.
Esté preparado para utilizar cualquier tipo de función que haya sido revisada en este capítulo.
Un trabajo de verano paga tiempo y medio por horas extras si un trabajador trabaja más de 40 horas. Después de 40 horas, al trabajador se le paga 1.5 veces la tarifa horaria de\($12.00\) por hora.
- Escribir y graficar una función por partes que da el pago semanal P en cuanto al número de horas trabajadas h. SUMINISTRO: Esto puede ser complicado, piensa en cómo expresar el número de horas por encima de 40.
- ¿Cuánto se ganará trabajando 45 horas?
Solución
- Para escribir la función por partes:
\(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)
Para graficar esta función, haz una tabla de soluciones:
|
Tabla de soluciones para\(P (h) = 12h \) Dominio\(0 < h \leq 40\) |
|
| \(h\) | \(P(h)\) |
| 1 | \($12.00\) |
| 10 | \($120.00\) |
| 40 | \($480.00\) |
|
Tabla de soluciones para\(P (h) = 12(40) + 1.5(7)(h − 40) \) Simplificado\(P (h) = 18h − 240 \) Dominio\(h > 40\) |
|
| \(h\) | \(P(h)\) |
| 41 | 498 |
| 45 | 570 |
| 50 | 660 |
| 60 | 840 |
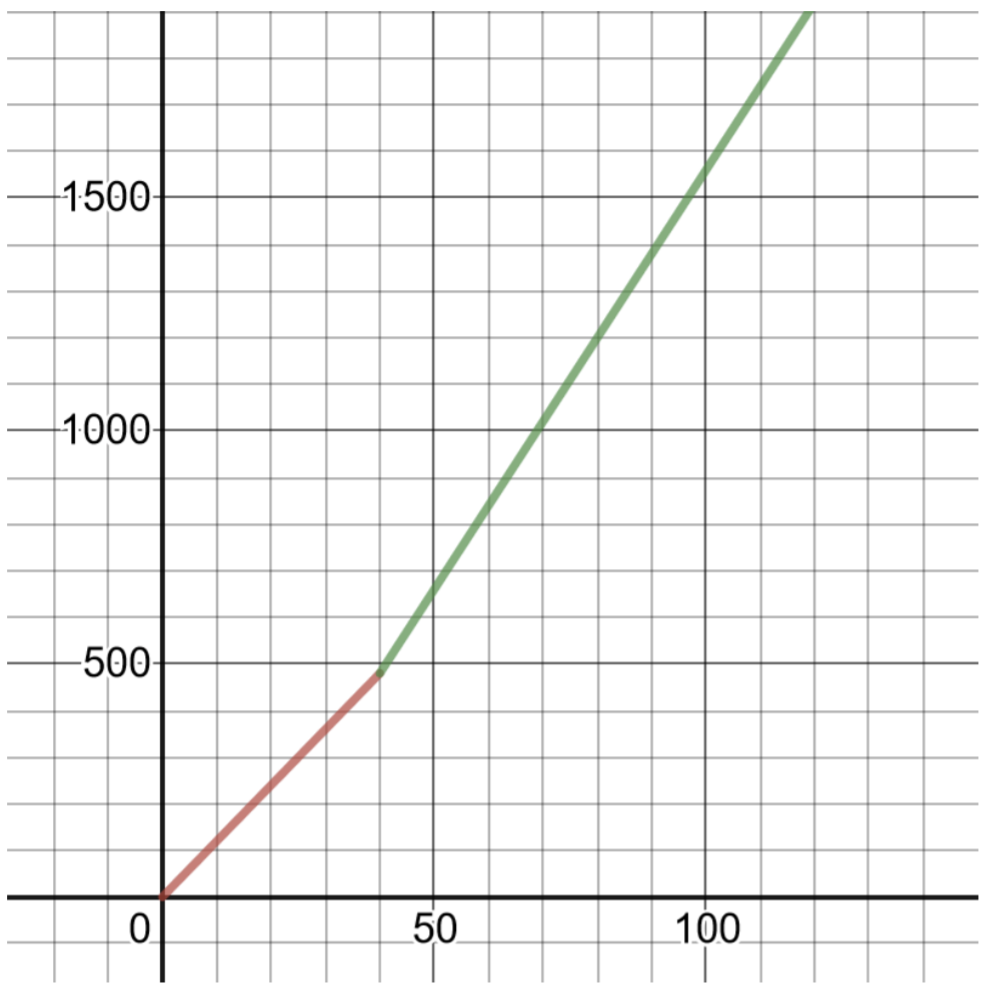
- \($570.00\)por 45 horas de trabajo (ver Tabla de Soluciones)
La NASA lanza un cohete a los\(t=0\) segundos. Su altura, en metros sobre el nivel del mar, en función del tiempo viene dada por\(h(t) = −4.9t^2 + 46t + 227\).
- Suponiendo que el cohete salpique hacia el océano, ¿a qué hora ocurre el chapoteo?
- ¿Qué tan alto por encima del nivel del mar llega el cohete en su apogeo?
Solución
- Al chapotear hacia abajo\(h(t) = 0\),, así que establece la función igual a 0 y resuelve para\(t\).
\(0 = −4.9t 2 + 46t + 227\)
Usa la Fórmula Cuadrática para resolver esta ecuación, con\(a = −4.9\)\(b = 46\),\(c = 227\)
\(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)
- ¿Qué tan alto por encima del nivel del mar llega el cohete en su apogeo?
El signo del coeficiente del término principal de la función cuadrática\(h(t) = −4.9t^2 + 46t + 227\) muestra en qué dirección se abre la parábola. El coeficiente es\(−4.9\), y como es negativo, la función cuadrática se abre hacia abajo.
Ahora necesitamos encontrar el vértice. El valor y del par ordenado de vértices mostrará dónde comienza el rango.
El vértice es\(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\), con\(a = −4.9\) y\(b = 46\)
El vértice es\(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)
El vértice es\((4.694, f (4.694))\) que es\((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\) o\((4.694, 334.959)\)
La altura del cohete en su pico es de\(334.959\) metros sobre el nivel del mar.
Para promover las ventas grupales para un crucero por Alaska, una agencia de viajes reduce el precio regular de los boletos\($4500\)\($5\) por cada persona del grupo.
- Escribe una ecuación lineal que dé el costo por persona\(f(p)\), si la\(p\) gente viaja en el grupo.
- Usa la ecuación para determinar el costo para 50 personas.
Solución
- Dado que el costo por persona se reduce la misma cantidad para cada persona, esta es una ecuación lineal.
\(f(x) = mx + b\)Utilízalo, o vamos a escribirlo como\(f(p) = mp + b\), con\(f(p)\) el costo por persona.
\(f(p) = mp + b\)
Dado que el costo por persona se reduce en $5 por cada persona del grupo, esa es la pendiente de la línea.
\(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)
- Usa la ecuación para determinar el costo para 50 personas.
\(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)
Complete los siguientes problemas de función aplicada:
- Un sastre cobra una tarifa básica de\($20\) más\($5\) por letra para coser el nombre de un atleta en la parte posterior de una chaqueta.
- Escribe una ecuación lineal que encuentre el costo de tener un nombre que contenga x letras cosidas en la parte posterior de una chaqueta.
- ¿Cuál es el costo de un nombre con 11 letras?
- En Acapulco, México, una atracción turística popular es ver a los hombres bucear desde un acantilado hasta el agua a 75 pies debajo. La altura de un buceador\(f(t)\) por encima del agua (en pies),\(t\) segundos después del buceo, es dada por\(f(t) = −16t^2+75\).
- ¿Cuánto dura una inmersión?
- En un determinado país, el impuesto sobre la renta se evalúa de la siguiente manera: No hay impuesto sobre la renta hasta\($15000\). Los ingresos superiores\($15000\) y superiores\($30000\) se gravan a\(12%\). Los ingresos superiores\($30000\) se gravan a\(18%\).
- Escriba la función por partes de la información anterior y esboce su gráfica.
- Determinar la cantidad de impuesto a pagar sobre un ingreso de\($18000\).


