2.1: Números y Números
- Page ID
- 113194
Necesitará: Bloques A (Tarjetas de Material 2A, 2B, 2C, 2D, 2E)
Imagina que te encontraste con una persona de una remota colonia angloparlante donde todos tenían tres dedos en cada mano. A pesar de que la gente de esta colonia era inteligente, nunca habían oído hablar de contar y no sabían qué era, qué significaba ni cómo hacerlo. No sabían nada de números, cómo eran, cómo se les llamaba o cómo se veían. Piensa en cómo podrías enseñarle a esta persona sobre el conteo y los números para que pueda regresar y compartir este maravilloso conocimiento con sus amigos. ¿Qué herramientas usarías para enseñar? ¿Cuáles son algunos de los conceptos que tendrías que transmitir? ¿Qué dificultades pueden surgir? ¿Crees que esto sería una tarea fácil o difícil? Escribe algunas de tus ideas, estrategias y conclusiones.
¿Qué recuerdas de aprender sobre números o cómo contar? ¿Alguna vez has ayudado a enseñarle a un niño pequeño a contar? Si es así, ¿cómo fue? ¿Cuánto tiempo crees que le toma a alguien aprender a contar por primera vez?
La mayoría de nosotros en el mundo moderno prácticamente damos por sentado el concepto de números y contar. De hecho, damos por sentado el lenguaje, pero ese tema está demasiado involucrado para entrar en este momento. Imagínese el gran avance que fue cuando la gente pensó por primera vez en dar nombres a los objetos. Eventualmente usaron palabras, a las que llamaremos nombres de números, para describir conjuntos de objetos (¿recuerdas conjuntos?!) en términos de su tamaño. Esto fue un avance matemático considerable. Aunque todavía hay algunas culturas que no han asignado nombres para números mayores a tres, la mayoría de las culturas han desarrollado este concepto. Algunas tribus incluso tienen diferentes nombres de números para diferentes tipos de objetos.
Una dificultad con el concepto de números tal como los usamos hoy en día es que son conceptos y no necesariamente utilizados sólo para contar objetos. El número cuatro, por ejemplo, se usa de muchas maneras —cuatro años, cuarto 4, cuatro pies de altura, 4 niños, cuatro horas, cuatro minutos después de las ocho, estación de correo 4, 4 dedos, un grado de 4 en un quiz, contar hasta 4, cuatro veces más grande que algo, 4to lugar, cuatro deseos, cuarto en línea, llamada 444-4444, código 44, etc.
Entonces, ¿qué es un número?
Bueno, un número es una idea abstracta que representa una cantidad. No puedes ver ni tocar un número. Los símbolos que vemos y tocamos que se utilizan para representar números son en realidad números. Un numeral se compone de uno o más símbolos. En el sistema hindu-árabe que utilizamos, los números están conformados por uno o más de estos diez símbolos —0,1,2,3,4,5,6,7,8 y 9. Por ejemplo, en el sistema hindu-árabe, el número tres se representa escribiendo el número tres que escribimos así: 3 y el número dos millones se representa escribiendo el número dos millones que escribimos así: 2 millones. Observe, se necesitó un símbolo para escribir el número de tres y siete símbolos para escribir el número por dos millones (no contamos las comas como símbolos porque no son esenciales para escribir el número). Aunque se necesitaron siete símbolos para escribir el número dos millones, tenga en cuenta que solo hay dos símbolos diferentes utilizados para escribir ese número: dos (2) y un cero (0).
En sus propias palabras, describa la palabra número.
En sus propias palabras, describa la palabra numeral.
Hay tres usos comunes de los números. Describir cuántos elementos hay en un conjunto finito es el uso más común de los números de conteo. Cuando se usa de esta manera, el número se denomina número cardinal. Otra forma en que se usan los números se refiere al orden. Por ejemplo, alguien podría ser el ganador del quinto lugar o tú podrías ser el octavo en la fila. Cuando se usan de esta manera, los números se denominan números ordinales. También hay números utilizados para identificación como su número de teléfono, código postal, número de seguro social o número de tarjeta de crédito. Estos se llaman números de identificación y es el orden real de los símbolos lo que es importante, no el valor del número
Cuando la gente reconoció que una colección de cuatro guijarros y una colección de cuatro plátanos tenían una propiedad común, estaban aprendiendo el concepto de emparejar. Saca tus bloques A y divídalos en subconjuntos según el color. Tome el subconjunto de bloques A rojos y el subconjunto de bloques A azules. Haremos coincidir cada elemento en los bloques A azules con un elemento en los bloques A rojos. Hay varias formas de hacer esto. Voy a mostrar dos formas de igualarlos. Muestra una manera diferente de emparejarlos en Coincidencia #3 a continuación.
| COINCIDENCIA #1 | COINCIDENCIA #2 | COINCIDENCIA #3 |
|---|---|---|
| SBT\(\leftrightarrow\) LRT | SBT\(\leftrightarrow\) SRQ | |
| \(\leftrightarrow\)SRT LBT | LBT\(\leftrightarrow\) LRQ | |
| SBQ\(\leftrightarrow\) LRQ | SBQ\(\leftrightarrow\) SRC | |
| LBQ\(\leftrightarrow\) SRQ | LBQ\(\leftrightarrow\) LRC | |
| SBC\(\leftrightarrow\) LRC | SBC\(\leftrightarrow\) SRT | |
| LBC\(\leftrightarrow\) SRC | LBC\(\leftrightarrow\) LRT |
Las imágenes se pueden usar para representar una coincidencia. A continuación se muestra otra forma de mostrar Matching #1:
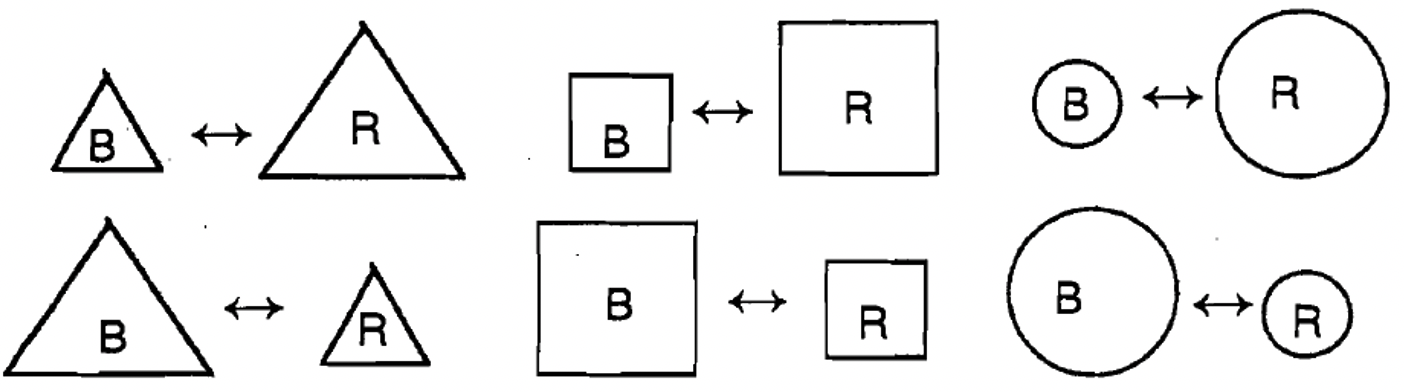
Decimos que el conjunto de bloques A azules coincide con el conjunto de bloques A rojos porque podemos emparejar cada elemento de los bloques A azules con exactamente un elemento de los bloques A rojos.
Usando imágenes, se muestra una coincidencia entre los triángulos grandes y los círculos pequeños. Hay más de una manera posible de emparejarlos. Asegúrate de que cada triángulo grande esté “bailando” con uno de los círculos pequeños.
NOTA: Dos conjuntos que combinan NO tienen que combinar de una manera natural o agradable la forma en que podríamos combinar los colores de nuestra ropa juntos. Podría ser más fácil pensar en la palabra emparejamiento en su lugar. Piensa en mostrar una coincidencia entre dos sets tomando un elemento en el primer set y emparejándolo para bailar con un elemento en el segundo set. Ahora que están “bailando” juntos, toma otro elemento del primer set y elige a alguien del segundo set para que baile con él. ¡Sigue haciendo esto hasta que todos los elementos estén emparejados y bailando! Esto es un emparejamiento. Si tu primer set tuviera 5 chicas y tu segundo set tuviera 4 chicos, no coincidirían porque una chica se quedaría sin pareja. Es por ello que es necesario tener el mismo número de elementos en cada conjunto para poder representar una coincidencia.
Ahora emparejemos el subconjunto de Círculos con el subconjunto de Cuadrados. A continuación se muestran dos emparejamientos diferentes. Nota He utilizado diferentes formatos que en el ejercicio 5.
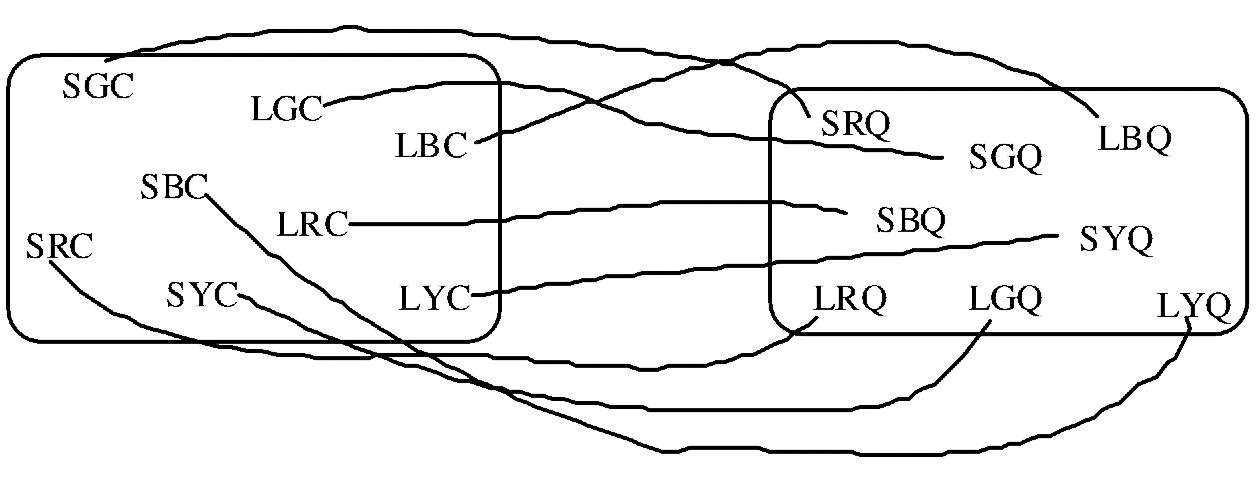
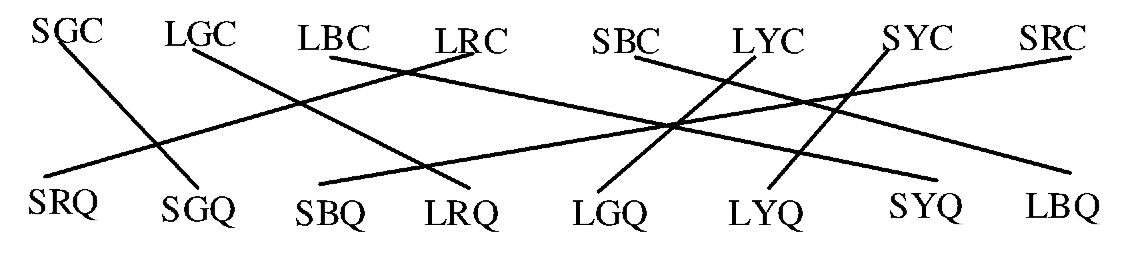
Mostrar dos formas diferentes de hacer coincidir el conjunto de triángulos pequeños con el conjunto de cuadrados grandes.
Cada una de las parejas que hemos emparejado hasta ahora ilustra una correspondencia uno a uno (1-1) entre dos conjuntos. Decimos que dos conjuntos coinciden si hay una correspondencia uno a uno entre sus elementos.
Si existe una correspondencia 1-1 entre dos conjuntos, ¿qué implica eso sobre la cardinalidad de los dos conjuntos?
Dibuja una correspondencia uno a uno entre los elementos de los conjuntos a continuación.
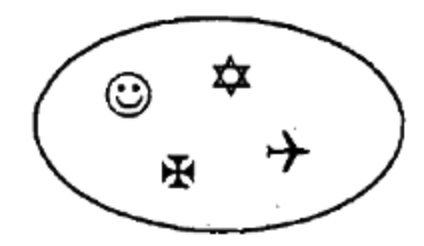 |
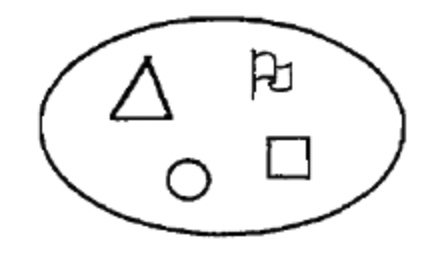 |
Para mostrar todas las correspondencias 1-1, o emparejamientos entre dos sets, pienso en todas las formas en que dos sets podrían asociarse para hacer un solo baile en la pista de baile. Todos de cada set obtienen exactamente una pareja del otro set con la que bailar, y todos llegan a bailar. Por ejemplo, piensa en un grupo de 4 chicos —A, B, C y D y 4 chicas— W, X, Y y Z. Cada chico necesita ser emparejado con una chica para un baile, así que habrá cuatro parejas bailando para un baile. Una coincidencia sería mostrar cómo se emparejan para ese baile: tal vez A con X, B con Z, C con W y D con Y —es decir Matching 11, como se muestra a continuación. Eso es sólo una coincidencia. Tenga en cuenta que no empareja un elemento de un conjunto con un elemento del mismo conjunto. Para este ejemplo, eso significa que una niña solo baila con un niño. Para mostrar TODAS las posibilidades para este ejemplo, tendrías que enumerar todas las diferentes formas en que podrían terminar como parejas en la pista de baile para un baile. Cada coincidencia muestra a las cuatro parejas, ya que están emparejadas para un baile. Para ser un emparejamiento diferente, al menos dos parejas habrían cambiado de pareja. En realidad hay 24 posibles correspondencias 1-1 (o diferentes emparejamientos) para este ejemplo de cuatro niños y cuatro niñas. A continuación se muestra una forma de enumerar todas estas posibilidades:
|
Coincidencia 1 A\(\leftrightarrow\) W B\(\leftrightarrow\) X C\(\leftrightarrow\) Y D\(\leftrightarrow\) Z |
Coincidencia 2 A\(\leftrightarrow\) W B\(\leftrightarrow\) X C\(\leftrightarrow\) X D\(\leftrightarrow\) Y |
Coincidencia 3 A\(\leftrightarrow\) W B\(\leftrightarrow\) Y C\(\leftrightarrow\) X D\(\leftrightarrow\) Z |
Coincidencia 4 A\(\leftrightarrow\) W B\(\leftrightarrow\) Y C\(\leftrightarrow\) Z D\(\leftrightarrow\) X |
Coincidencia 5 A\(\leftrightarrow\) W B\(\leftrightarrow\) Z C\(\leftrightarrow\) X D\(\leftrightarrow\) Y |
Coincidencia 6 A\(\leftrightarrow\) W B\(\leftrightarrow\) Z C\(\leftrightarrow\) Y D\(\leftrightarrow\) X |
|
Coincidencia 7 A\(\leftrightarrow\) X B\(\leftrightarrow\) W C\(\leftrightarrow\) Y D\(\leftrightarrow\) Z |
Coincidencia 8 A\(\leftrightarrow\) X B\(\leftrightarrow\) W C\(\leftrightarrow\) Z D\(\leftrightarrow\) Y |
Coincidencia 9 A\(\leftrightarrow\) X B\(\leftrightarrow\) Y C\(\leftrightarrow\) W D\(\leftrightarrow\) Z |
Coincidencia 10 A\(\leftrightarrow\) B\(\leftrightarrow\) Y C\(\leftrightarrow\) W D\(\leftrightarrow\) Z |
Coincidencia 11 A\(\leftrightarrow\) X B\(\leftrightarrow\) Z C\(\leftrightarrow\) W D\(\leftrightarrow\) Y |
Coincidencia 12 A\(\leftrightarrow\) X B\(\leftrightarrow\) Z C\(\leftrightarrow\) Y D\(\leftrightarrow\) W |
|
Coincidencia 13 A\(\leftrightarrow\) Y B\(\leftrightarrow\) W C\(\leftrightarrow\) X D\(\leftrightarrow\) Z |
Coincidencia 14 A\(\leftrightarrow\) Y B\(\leftrightarrow\) W C\(\leftrightarrow\) Z D\(\leftrightarrow\) X |
Coincidencia 15 A\(\leftrightarrow\) Y B\(\leftrightarrow\) X C\(\leftrightarrow\) W D\(\leftrightarrow\) Z |
Coincidencia 16 A\(\leftrightarrow\) Y B\(\leftrightarrow\) X C\(\leftrightarrow\) Z D\(\leftrightarrow\) W |
Coincidencia 17 A\(\leftrightarrow\) Y B\(\leftrightarrow\) Z C\(\leftrightarrow\) W D\(\leftrightarrow\) X |
Coincidencia 18 A\(\leftrightarrow\) Y B\(\leftrightarrow\) Z C\(\leftrightarrow\) X D\(\leftrightarrow\) W |
|
Coincidencia 19 A\(\leftrightarrow\) Z B\(\leftrightarrow\) W C\(\leftrightarrow\) Y D\(\leftrightarrow\) X |
Coincidencia 20 A\(\leftrightarrow\) Z B\(\leftrightarrow\) W C\(\leftrightarrow\) X D\(\leftrightarrow\) Y |
Coincidencia 21 A\(\leftrightarrow\) Z B\(\leftrightarrow\) X C\(\leftrightarrow\) W D\(\leftrightarrow\) Y |
Coincidencia 22 A\(\leftrightarrow\) Z B\(\leftrightarrow\) X C\(\leftrightarrow\) Y D\(\leftrightarrow\) W |
Coincidencia 23 A\(\leftrightarrow\) Z B\(\leftrightarrow\) Y C\(\leftrightarrow\) W D\(\leftrightarrow\) X |
Coincidencia 24 A\(\leftrightarrow\) Z B\(\leftrightarrow\) Y C\(\leftrightarrow\) X D\(\leftrightarrow\) W |
Si se le pidió que enumerara una coincidencia entre dos conjuntos {A, B, C, D} y {W, X, Y, Z}, cualquiera de los 24 emparejamientos mostrados arriba estaría bien. No obstante, si se le pide que enumere TODAS las posibilidades, debe tener muy claro qué constituye una coincidencia, como he ilustrado anteriormente. En cada coincidencia, anotar los emparejamientos individuales (quien esta bailando con quien) deben mostrarse. Si los conjuntos tienen un elemento cada uno, entonces cada coincidencia tiene un emparejamiento. Si los conjuntos tienen dos elementos cada uno, entonces cada coincidencia tiene dos emparejamientos. Si los conjuntos tienen tres elementos cada uno, entonces cada coincidencia tiene tres emparejamientos. Y, si los conjuntos tienen cuatro elementos cada uno (como en el ejemplo anterior), entonces cada coincidencia tiene cuatro emparejamientos.
Consulta si notas algún patrón arriba antes de continuar. Es mucho más fácil mostrar los emparejamientos cuando hay menos elementos en los sets. Si hay un elemento en cada conjunto, entonces es como estar en una isla desierta, un hombre y una mujer. No hay mucha elección, ¿verdad?
Mostrar cada correspondencia (o coincidencia) 1-1 posible entre los conjuntos.
| a. {1} y {A} | b. {2,3} y {B, C} | c. {4,5,6} y {D, E, F} |
Es importante darse cuenta de que los dos conjuntos que se están emparejando pueden contener uno, algunos o todos los mismos elementos. Estudia los siguientes ejemplos, donde cada conjunto contiene exactamente los mismos elementos.
Ejemplos: Mostrar cada correspondencia (o coincidencia) 1-1 posible entre los conjuntos enumerados.
{3} y {3}
Solución
Coincidencia 1
3\(\leftrightarrow\) 3
{6, 7} y {6, 7}
Solución
|
Coincidencia 1 6\(\leftrightarrow\) 6 7\(\leftrightarrow\) 7 |
Coincidencia 2 6\(\leftrightarrow\) 7 7\(\leftrightarrow\) 6 |
{a, b, c} y {a, b, c}
Solución
|
Coincidencia 1 a\(\leftrightarrow\) a b\(\leftrightarrow\) b c\(\leftrightarrow\) c |
Coincidencia 2 a\(\leftrightarrow\) a b\(\leftrightarrow\) c c\(\leftrightarrow\) b |
Coincidencia 1 a\(\leftrightarrow\) b b\(\leftrightarrow\) a c\(\leftrightarrow\) c |
Coincidencia 1 a\(\leftrightarrow\) a b\(\leftrightarrow\) b c\(\leftrightarrow\) c |
Coincidencia 1 a\(\leftrightarrow\) a b\(\leftrightarrow\) b c\(\leftrightarrow\) c |
Coincidencia 1 a\(\leftrightarrow\) a b\(\leftrightarrow\) b c\(\leftrightarrow\) c |
Mostrar cada correspondencia (o coincidencia) 1-1 posible entre los conjuntos enumerados. Este ejercicio continúa en la página siguiente. Etiquetar los emparejamientos, así queda claro cuántos emparejamientos hay, y qué pares hay en cada coincidencia.
| a. {M} y {M} | b. {x, y} y {x, z} | c. {1, 2} y {1, 2} | d. {1, 2, 3} y {1, 2, 3} | e. {1, 2, 3} y {3, 4, 5} |
Si debes enumerar todas las correspondencias 1-1 posibles entre 2 series, cada una teniendo la cardinalidad listada a continuación, ¿cuántos emparejamientos posibles hay?
| a. 1 elemento cada uno: ___ | b. 2 elementos cada uno: ___ | c. 3 elementos cada uno: ___ |
La fórmula para averiguar el número de correspondencias 1-1 entre conjuntos que tienen n elementos es n! (esto se lee “n factorial”). ¡Para averiguar qué número n! es, multiplicar todo el número de conteo juntos hasta n. ¡Por ejemplo, 1! = ¡1, 2! = 1\(\cdot\) 2 = 2, 3! = 1\(\cdot\) 2\(\cdot\) 3 = 6, ¡y 4! = 1\(\cdot\) 2\(\cdot\) 3\(\cdot\) 4 = 24. En el primer ejemplo donde enumeré todos los emparejamientos posibles para dos conjuntos, cada uno con 4 elementos, había 24 posibilidades. ¿Obtuviste el número correcto de posibilidades para todas las que hiciste?
Es hora de señalar algunas propiedades sencillas pero importantes de la coincidencia.
Un conjunto siempre coincide con sí mismo.
Dos conjuntos que coinciden no tienen por qué ser diferentes entre sí. Por ejemplo, podrías hacer coincidir {X, Y, Z} con {X, Y, Z} mostrando esta correspondencia natural uno-a-uno: X “X, Y “Y y Z “Z. (O puedes emparejarlos de alguna otra manera. Aquí hay otras dos formas de mostrar una coincidencia: X “Z, Y “X y Z “Y O X “X, Y “Z y Z “Y.)
Para cualquiera de dos conjuntos A y B, si A coincide con B, entonces B coincide con A.
Esta propiedad enfatiza que el orden en que se mencionan los conjuntos es irrelevante.
Para tres conjuntos cualesquiera, si A coincide con B y B coincide con C, entonces A coincide con C.
Ilustra la Propiedad 3 dejando que A sea el conjunto de círculos pequeños, B sea el conjunto de triángulos pequeños y C sea el conjunto de cuadrados pequeños. ¡Enumere las abreviaturas (SRC, etc.) o dibuje el cuadro para cada uno de los elementos individuales de cada conjunto! Deberían mostrarse tres emparejamientos separados, cada uno con 4 emparejamientos. La primera coincidencia debe mostrar una coincidencia entre A y B, luego debe haber otra coincidencia mostrada entre B y C. Por último, debe haber una coincidencia mostrada entre A y C.
|
Coincidencia entre A y B: |
Coincidencia entre B y C: |
Coincidencia entre A y C: |
Hoy en día, la mayoría pero no todas las civilizaciones alrededor del mundo utilizan el sistema hindu-árabe de conteo y números 1,2,3,4,5,6,7,8,9,10,11,12,... Hay muchas ventajas en este sistema de números. Si bien podría pensar que este sistema común y ampliamente utilizado de contar la elección obvia, podría considerar tanto las ventajas como las desventajas del hindu-árabe a medida que aprendemos sobre otros sistemas de numeración.
Considera el sistema Stroke donde solo había un símbolo, un simple trazo vertical, para expresar un número. Un trazo vertical como este, |, expresó uno. Para expresar el número siete, escribirías siete trazos: | | | | | | |
a. Muestra cómo escribirías el numeral once en TROCHE:
b. Describa con palabras cómo escribir los números quinientos doce; y dos millones en TROQUEO. No intente escribir los trazos reales!! ¡Solo tenemos un semestre!
Nombra algunas ventajas y desventajas del sistema STROTE, en comparación con el sistema Hindu-Árabe.
El sistema de conteo mejoró el sistema STROTE al introducir el concepto de agrupación. Probablemente estés familiarizado con este sistema donde se colocó el quinto trazo a través de los cuatro anteriores por lo que sería más fácil de leer ya que puedes contar por cinco. Stroke es un sistema de símbolo único, pero Tally se puede considerar como un sistema de dos símbolos, aunque el segundo símbolo en realidad solo está compuesto por cinco trazos. Observe la diferencia en escribir el número veintiocho en los dos sistemas.
|
Sistema Stroke: ||||||||||||||||||||||||||||||| |
Sistema Tally: \(\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}|||\) |
a. Escriba el numeral para 17 en TROCHE.
b. Escribe el número para 17 en Tally.
Si piensas en un solo trazo (|) como un símbolo y el conteo de 5 tiempos (\(\cancel{||||}\)) como un símbolo separado, entonces se necesitan ocho símbolos para expresar el número para 28 como se muestra arriba Ejercicio 13. En TROCHE, se necesitaron 28 símbolos para escribir el mismo número. ¿Cuántos símbolos se necesitan para expresar el numeral para 172 en TALY?
El antiguo sistema numérico egipcio que se desarrolló alrededor del 3400 a.C., emplea un sistema aditivo de conteo, donde los símbolos del numeral no tienen que estar en ningún orden especial o incluso en una línea que va de izquierda a derecha. A continuación se enumeran los siete símbolos de este antiguo sistema, junto con sus equivalentes hindu-árabes.
 |
 |
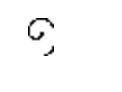 |
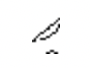 |
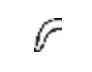 |
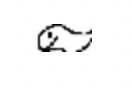 |
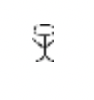 |
| Staff | Hueso del talón | Scroll | Flor de loto | Dedo señalador | Polliwog | Hombre asombrado |
| Uno | Diez | Cien | Mil | Diez mil | Cien mil | Millones |
| 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1,000,000 |
Aquí hay tres formas diferentes de escribir el número sesenta y cinco en el antiguo sistema egipcio:
| \(\cap\cap\cap\cap\cap\cap\)|||||| | o | \(\cap\cap\||\cap|\cap\cap||\cap\) |
o como se muestra a continuación con todos los símbolos encerrados en un conjunto visual
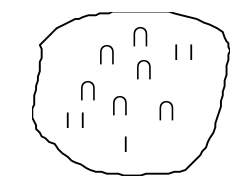
Simplemente se suman los valores de cada uno de los símbolos para obtener la respuesta.
El principio aditivo establece que el valor de un conjunto de símbolos es la suma del valor de los símbolos
En este sistema aditivo, el número egipcio representa
1,000,000 + 10,000 + 1,000 + 1,000 + 1,000 + 100 + 100 + 1 + 1 + 1 + 1 = 1,013,204.
Recuerde: El orden en que se escriben los símbolos es irrelevante en un sistema aditivo.
Además de poder escribir los símbolos del numeral en cualquier orden, también puede usar una combinación diferente de símbolos utilizados para representar el mismo número. Aquí hay dos formas diferentes de escribir el número para ciento veintitrés:
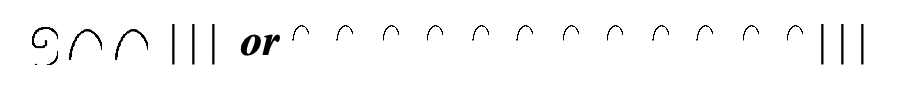
Explica con palabras dos formas más en las que podrías escribir el número ciento veintitrés usando una combinación de símbolos diferente a la mostrada arriba.
A continuación se muestra un recordatorio de lo que representa cada símbolo para poder hacer los siguientes ejercicios.
 |
 |
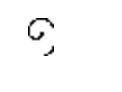 |
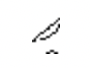 |
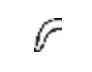 |
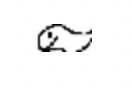 |
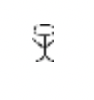 |
| Staff | Hueso del talón | Scroll | Flor de loto | Dedo señalador | Polliwog | Hombre asombrado |
| Uno | Diez | Cien | Mil | Diez mil | Cien mil | Millones |
| 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1,000,000 |
Exprese cada número egipcio a continuación como un número hindu-árabe. Mostrar trabajo.
|
a.  |
|
b.  |
|
c. 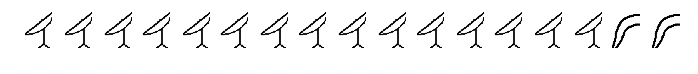 |
|
d.  |
Exprese cada número hindu-árabe a continuación como un número egipcio usando el menor número de símbolos posible. Mostrar trabajo.
| a. 407 |
| b. 3,051,040 |
| c. 232,501 |
| d. 4,000,000 |
| e. 1,111,111 |
El sistema egipcio emplea la técnica de agrupación, donde un cierto número de los mismos símbolos se agrupan y se reemplazan por un nuevo símbolo. Esto es necesario para simbolizar números muy grandes de manera eficiente. Se dice que los sistemas que utilizan este principio de agrupación son de cierta base dependiendo de cuántos símbolos se necesitan para intercambiar a un nuevo símbolo. Por ejemplo, se dice que un sistema que agrupa seis símbolos y luego los reemplaza por un nuevo símbolo es un sistema Base Seis.
¿En qué base está el sistema egipcio? ¿Cuál es la limitación de este sistema en lo que respecta a la agrupación? (¡Piensa en cómo escribir cuatro billones!)
Nombra algunas ventajas y desventajas del sistema del Antiguo Egipto en comparación con el sistema Hindu-Árabe, el sistema Stroke y el sistema Tally.
Aquí hay ejemplos de algunos números romanos: XVI, MCMLX, XIX, xii, iv, iii. Nombra algunos lugares que todavía veas números romanos hoy en día.
Crédito Extra: Publica una foto en el Foro de Números Romanos en el mundo real. Debe ser tu propia foto no una copiada de internet u otra fuente. Asegúrate de estar en la imagen e incluir el valor como un número hindu-árabe.
El sistema de numeración romana estuvo en uso por 300 a.C. A continuación se listan los números romanos básicos y sus valores correspondientes. Estaremos escribiendo con letras mayúsculas.
| I: 1 | V: 5 | X: 10 | L: 50 | C: 100 | D: 500 | M: 1000 |
Originalmente, el Sistema de Numeración Romana era un sistema aditivo simple —por ejemplo, DCCCLXXXVII = 500 + 100 + 100 + 100 + 50 + 10 + 10 + 10 + 5 + 1 + 1 = 887. En realidad es un sistema Base Diez con símbolos adicionales para 5, 50 y 500. Estos símbolos adicionales reducen significativamente la cantidad de escritura que uno debe hacer. Por ejemplo, escribir el número romano ochocientos ochenta y siete sin el uso de los símbolos adicionales se vería así: CCCCCCXXXXXXXXIIIIIIII. Escribir este mismo numeral usando los símbolos adicionales se vería así: DCCCLXXXVII. Sin la V, L y D, se necesitaría escribir más del doble de símbolos para este numeral en particular.
Escribe cada número Hindu-Árabe como un número romano usando la menor cantidad de símbolos:
| a. 32: | b. 561: |
| c. 708: | d. 2053: |
Escribe cada número romano como un número hindu-árabe y muestra el trabajo:
| a. MMDCLXXXV11: ____ | b. MCCXXXII:_____ |
El sistema de numeración romana desarrolló e incorporó cambios a lo largo del tiempo. Una limitación de un sistema aditivo simple es que eventualmente te quedas sin símbolos para números muy grandes. ¿Ya lo averiguaste al responder al ejercicio 19? Los romanos idearon una manera inteligente de encargarse de este problema. Si se colocaba una barra sobre un símbolo o conjunto de símbolos, indicaba que ese número se iba a multiplicar por mil. Se podría usar más de una barra en cualquier símbolo o conjunto de números dados. Por ejemplo, dos barras indicaron que el número se iba a multiplicar por 1000 1000 (o un millón). En pocas palabras, los símbolos con una barra sobre ellos están en miles, los que tienen dos barras sobre ellos están en millones, los que tienen tres barras sobre ellos están en los miles de millones y así sucesivamente. Así, el sistema de numeración romana es multiplicativo así como aditivo. Estudie esta característica en los siguientes ejemplos:
\(\bar{\text{CCLVI}}\)CCX = (100 + 100 + 50 + 5 + 1) 1000 + 100 + 100 + 10 = 256,210
\(\bar{\bar{\text{V}}\text{LX}}\)DX = 5 1000000 + (50 + 10) 1000 + 500 + 10 = 5,060,510
Escribe cada número hindu-árabe como un número romano usando la menor cantidad de símbolos posible.
| a. 330,802 ____ | b. 70,001,651 ____ |
Escribe cada número romano como un número hindu-árabe: Mostrar obra.
| a.\(\bar{\text{III}}\) CCXII | b.\(\bar{\text{LX}}\) DCL |
Con el tiempo, el sistema de numeración romana desarrolló un principio sustractivo. Si un símbolo que representa un número menor está a la izquierda de un símbolo que representa un número mayor, entonces el valor total de esos dos símbolos juntos representa el valor del símbolo más grande menos el valor del símbolo más pequeño. Hubo condiciones específicas. Solo los símbolos que representan potencias de diez (I, X, C, M) podrían restarse y cada uno de estos cuatro solo podría emparejarse con los siguientes dos símbolos más grandes. Entonces, las siguientes son las únicas posibilidades para usar el principio sustractivo:
| IV: 4 | IX: 9 | XL: 40 | XC: 90 | CD: 400 | CM: 900 |
Al leer un número romano de izquierda a derecha, use el principio aditivo. Si un símbolo que denota un valor menor precede a un símbolo que denota un valor mayor, use el principio sustractivo al leer esos dos símbolos. Estudie los siguientes ejemplos:
CMXXXIX = (1000-100) + 10 + 10 + (10 - 1) = 939
\(\bar{\text{XCIV}}\)CCXCII = (100-10 + 5-1) 1000 + 100 + 100 + (100-10) + 1 + 1 = 94,292
Reescribe cada número romano sin usar el principio sustractivo:
| a. CMXLIV: ____ |
| b. CDXCIX: ____ |
Reescribe cada número romano usando el menor número de símbolos posibles y el principio sustractivo cuando corresponda:
| a. CCCCCCCXXXIIIIIII ____ |
| b. MMMMMMMMMMMMCCCCXXXXXXXX ____ |
| c. CCCCCCCXXXXXXIIIIIIIIII ____ |
| d. CCCCXXXXII ____ |
Escriba cada número hindu-árabe como un número romano usando el menor número de símbolos posibles y el principio sustractivo cuando corresponda:
| a. 19,453 ____ |
| b. 2,849 ____ |
| c. 1,996 ____ |
A partir de ahora, porque así es como se usan hoy en día, escribe todos los números romanos usando el menor número de símbolos posibles y el principio sustractivo en su caso a menos que se le indique lo contrario.
Mi fecha de nacimiento es el 15 de julio de 1958. Si tuviera que escribir esta fecha como un número de seis dígitos (los dos primeros para el mes, los dos segundos para el día y los dos últimos para el año), escribiría 071558. Así se escribe 71,558 como número romano:\(\bar{\text{LXXI}}\) DLVIII.
Escribe tu fecha de nacimiento como un número de seis dígitos como lo hice para el mío arriba. Después, escríbelo en números romanos. Si lo prefieres, ¡puedes mentir o usar la fecha de nacimiento de alguien que amas!
Para números menores de mil, indique la mayor cantidad de veces que cada símbolo a continuación puede repetirse en una fila cuando se escribe como parte de un número romano. Supongamos que se utiliza el principio sustractivo.
En este conjunto de ejercicios, has aprendido algunos conceptos básicos de contar y también has aprendido sobre algunos sistemas de numeración. En el siguiente set, aprenderás sobre dos sistemas de numeración más. Terminaremos estos ejercicios comparando los sistemas con los que hemos trabajado hasta ahora. Primero, consideraremos el número de símbolos que uno tiene que memorizar para entender cada sistema individual. Luego determinaremos cuántos símbolos hay que anotar para representar varios números en los diferentes sistemas.
Para cada uno de los sistemas de numeración que hemos aprendido hasta ahora, indique cuántos símbolos diferentes tiene que memorizar una persona para entender el sistema. Para Roman, no consideres símbolos con barras sobre ellos como símbolos diferentes.
| a. Hindu-árabe: _____ | b. apoplejía: ____ | c. Contador: ____ | d. egipcio: ____ | e. Romano: ____ |
Escribamos el numeral 67 en los diferentes sistemas y anotemos cuántos símbolos totales (no necesariamente símbolos diferentes) se necesitan para expresar el número 67 en cada sistema.
| Hindu-Árabe: | Escribimos: 67 | 2 símbolos |
| TRAZO: |
Escribimos 67 trazos, se muestran a continuación ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| |
67 símbolos |
| Contador: |
Escribimos 13 grupos de conteo y 2 trazos, que se muestran a continuación \(\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||} ||\) |
15 símbolos |
| Egipcia: | Escribimos: | 13 símbolos |
| Romano: | Escribimos: LXVII | 5 símbolos |
Escriba el número para 900 en cada uno de los cinco sistemas siguientes y indique cuántos símbolos se necesitan para escribir el número completo. En lugar de escribir los números en STROCK y Tally, explica con palabras cómo los escribirías, indicando aún el número total de símbolos que tendrían que escribirse.
| a. Hindu-árabe: _____ | b. apoplejía: ____ | c. Contador: ____ | d. egipcio: ____ | e. Romano: ____ |
Por cada número hindu-árabe en la fila superior, indique el menor número de símbolos que se necesita para escribir el número en cada uno de los sistemas de numeración dados a la izquierda. Algunas respuestas son rellenadas para ti. No necesitas escribir realmente el numeral, solo determina cuántos símbolos tendrías que escribir si vas a escribir el número. Escribe tu respuesta en hindu-árabe.
| 143 | 400 | 1,000,000 | 30,009 | 2,124 | |
| Hindu-Árabe | 3 | 7 | |||
| Stroke | 30,009 | ||||
| Tally | 31 | 200,000 | |||
| Egipcia | 9 | ||||
| Roman | 2 |


