8.1: Raíces digitales y divisibilidad
- Page ID
- 113310
Es útil entender lo que se entiende por la RAÍZ DIGITAL de un número porque se utilizan en pruebas de divisibilidad, y también se utilizan para verificar problemas aritméticos. Una RAÍZ DIGITAL de un número es uno de estos dígitos: 0, 1, 2, 3, 4, 5, 6, 7 u 8.
Definición: La RAÍZ DIGITAL de un número es el resto obtenido cuando un número se divide por 9.
Divide cada uno de los siguientes números por 9. Después, escribe el resto.
| a. 25 | h. 8 |
| b. 48 | i. 54 |
| c. 53 | j. 74 |
| d. 829 | k. 481 |
| e. 5402 | l. 936 |
| f. 3455 | m. 8314 |
| g. 47522 | n. 647 |
A continuación se muestra otra forma más fácil de encontrar la raíz digital de un número.
Paso 1: Añadir los dígitos individuales del número.
Paso 2: Si hay más de un dígito después de sumar todos los dígitos, repita este proceso hasta obtener un solo dígito. Si la suma final es 9, escriba 0, porque 9 y 0 son equivalentes en raíces digitales (ya que el resto es un número menor que 9). Es por ello que la raíz digital de un número es sólo uno de estos dígitos: 0, 1, 2, 3, 4, 5, 6, 7 u 8. ¡Esos son los únicos restos posibles que se pueden obtener cuando un número se divide por 9! No puede ser 9. El único dígito con el que finalmente terminas es la RAÍZ DIGITAL del número.
Ejemplos: Encuentra las raíces digitales de los siguientes números.
34: Suma los dígitos: 3 + 4 = 7
La raíz digital de 34 es 7
321: Suma los dígitos: 3 + 2 + 1 = 6
La raíz digital de 321 es 6
58: Suma los dígitos: 5 + 8 = 13 Vuelva a sumar los dígitos: 1 + 3 = 4
La raíz digital de 58 es 4
97: Suma los dígitos: 9 + 7 = 16 Vuelva a sumar los dígitos: 1 + 6 = 7
La raíz digital de 97 es 7
72: Suma los dígitos: 7 + 2 = 9 En raíces digitales, 9 es lo mismo que 0
La raíz digital de 72 es 0
346,721: Suma los dígitos, obtenemos 3 + 4 + 6 + 7 + 2 + 1= 23 Vuelve a
sumar los dígitos: 2 + 3 = 5
La raíz digital de 346.725 es 5
Tenga en cuenta que no debe escribir 97 = 16 = 7. 97 NO ES IGUAL A 7!! La raíz digital de 97 es igual a 7. Yo uso guiones, dos puntos o flechas para grabar la raíz digital, así se ve algo así: 346,721\(\rightarrow\) 23\(\rightarrow\) 5. ¡¡¡¡¡¡¡¡No uses signos iguales!
Otro método para encontrar raíces digitales utiliza el hecho de que 9 y 0 son equivalentes en raíces digitales. El proceso de búsqueda de raíces digitales también se llama Casting out Nines. Cuando agregas los dígitos, no tienes que sumar el dígito 9 ni ninguna combinación de números que sumen 9 (como 2 y 7, o 5 y 4, o 2 y 3 y 4, etc.); puedes “desechar” todos los 9's. tacharlos; luego sumar los dígitos restantes juntos. El siguiente ejemplo ilustra cómo “echar nueves” simplifica el proceso de encontrar la raíz digital de un gran número.
Encuentra la raíz digital de 5.624.398.
Sin lanzar nueves: 5 + 6 + 2 + 4 + 3 + 9 + 8 = 37. Añadir de nuevo: 3 + 7 = 10. Añadir de nuevo: 1 + 0 = 1.
Fundición de nueves: Desde 5 y 4 suman hasta 9, tacharlos:\(\not{5}, 6, \not{24}, \not{398}\). Desde 6 y 3 suman hasta 9, también tacharlos:\(\not{5}, \not{6}, \not{24}, \not{398}\). También tachar el 9:\(\not{5}, \not{6}, \not{24}, \not{398}\). Los únicos dígitos a sumar son el 2 y el 8, que es 10. La raíz digital de 10 es 1. Entonces 1 es la raíz digital de 5,624,398 que es la misma respuesta obtenida sin primero echar nueves.
A continuación, las raíces digitales para los ejemplos 4, 5 y 6 de la página anterior se computan nuevamente utilizando el casting out nueves. Tenga en cuenta que la raíz digital sigue siendo la misma.
97: Tache el 9. Sólo queda el 7. La raíz digital es 7.
72:7 + 2 = 9, así que tacharlos. Por lo tanto, la raíz digital es 0.
346,721: Tocar el 3 y el 6, y también el 7 y 2. Los únicos dígitos a sumar son los 4 y 1. Por lo tanto, la raíz digital es 5.
Encuentra las raíces digitales de los siguientes números, usando cualquiera de los dos métodos. Recuerda que 9 no es una raíz digital. Escribe cero (0) si la suma es 9 (echa fuera el 9).
| a. 25 | h. 8 |
| b. 48 | i. 54 |
| c. 53 | j. 74 |
| d. 829 | k. 481 |
| e. 5402 | l. 936 |
| f. 3455 | m. 8314 |
| g. 47522 | n. 647 |
¿Obtuviste las mismas respuestas para los ejercicios 1 y 2?
Nota: Este método de encontrar la raíz digital solo tiene que ver con el número 9. No se puede encontrar el resto de un número al dividir por 7 sumando los dígitos.
El uso de Raíces Digitales es Verificar Problemas de Adición y Multiplicación.
Para verificar un problema de adición, agregue las raíces digitales de las adiciones. Entonces, verifique si la raíz digital de esa suma es la misma que la raíz digital de la suma real de las adiciones. Esto funciona si sólo hay dos adiciones, o varias adiciones.
A continuación se presentan algunos ejemplos de cómo verificar la adición. La suma real se muestra a la izquierda. Las flechas se utilizan para mostrar las raíces digitales de los apéndices y la suma. Para verificar, se suman las raíces digitales de los agregados, y luego se calcula la raíz digital de esa suma. Compárela con la raíz digital de la suma real. Si son iguales, ponga un cheque para indicar que la respuesta es probablemente correcta. NOTA: Existe una ligera posibilidad de que las raíces digitales coincidan, pero la respuesta aún no es correcta debido a algún otro error, como transponer dígitos. Por ejemplo, en el ejemplo 1 a continuación, es posible que alguien escriba 1153 para la respuesta. Las raíces digitales en el cheque coincidirían. La posibilidad de que esto suceda es leve, por lo que generalmente asumimos que el problema se hizo correctamente si las raíces digitales revisan. Por otro lado, si las raíces digitales no revisan, sabes que está mal.
\(\begin{aligned} 723 & \rightarrow 3 \\ \underline{+ 412} & \rightarrow 7 \\ 1135 & \rightarrow 1 \end{aligned}\)
Ck: 3 + 7 = 10\(\rightarrow\) 1 ¡\(\surd\)Correcto!
Explicación: Para verificar, agregue la raíz digital de las adiciones (3 + 7 = 10); luego busque la raíz digital de 10 (1). Verificar que esto sea igual a la raíz digital de la suma, 1135 (1). Como lo hace, el problema de adición probablemente se hizo correctamente.
\(\begin{aligned} 463 & \rightarrow 4 \\ \underline{+ 529} & \rightarrow 7 \\ 1630 & \rightarrow 1 \end{aligned}\)
Ck: 4 + 7 = 11\(\rightarrow\) 2 ¡Mal!
Explicación: Para verificar, agregue la raíz digital de las adiciones (4 + 7 = 11); luego busque la raíz digital de 11 (2). Esto debería ser igual a la raíz digital de la suma, 1630 (1). Como no lo hace, hay un error y el problema de adición se hizo incorrectamente.
Alguien hizo los siguientes problemas de adición, pero solo anotó las respuestas. Consulta la respuesta a cada problema mediante el uso de raíces digitales. Obsérvese que el procedimiento es el mismo si hay más de dos adiciones. Añadir las raíces digitales de todos los apéndices. ¡Muestra el trabajo!
| a.\(\begin{aligned} 4983 \\ \underline{+ 6829} \\ 10802 \end{aligned}\) | b.\(\begin{aligned} 5567 \\ \underline{+ 4987} \\ 10554 \end{aligned}\) | c.\(\begin{aligned} 3467 \\ \underline{+ 2541} \\ 5908 \end{aligned}\) |
| d.\(\begin{aligned} 8972 \\ 8876 \\ \underline{+ 5873} \\ 23721 \end{aligned}\) | e.\(\begin{aligned} 5873 \\ 3674 \\ \underline{+ 4763} \\ 13260 \end{aligned}\) | f.\(\begin{aligned} 4789 \\ 9835 \\ \underline{+ 5301} \\ 19925 \end{aligned}\) |
Para un problema de multiplicación, el cheque es similar, excepto para verificar, multiplicas las raíces digitales de los números que estás multiplicando. Para verificar la suma, AGREGAS las raíces digitales de las adiciones y se comprueba con la raíz digital de la suma. Para verificar la multiplicación, se MULTIPLICA la raíz digital de los números que se multiplican y se compara con la raíz digital del producto. Aquí hay algunos ejemplos que proporcionan una respuesta que alguien podría haber escrito después de hacer el problema de multiplicación en otra hoja de papel.
\(\begin{aligned} 85 & \rightarrow 13 \rightarrow 4 \\ \underline{\times 63} & \rightarrow 0 \\ 5355 & \rightarrow 18 \rightarrow 0 \end{aligned}\)
Ck: ¡\(4 \times 0 = 0\)Correcto!
Explicación: Para verificar, multiplica las raíces digitales de los números que estás multiplicando (\(4 \times 0 = 0\)); luego encuentra la raíz digital de 0 (0). Verificar que sea igual a la raíz digital del producto, 5355 (0). Como lo hace, el problema de multiplicación probablemente se hizo correctamente.
\(\begin{aligned} 43 & \rightarrow 7 \\ \underline{\times 52} & \rightarrow 7 \\ 2136 & \rightarrow 3 \end{aligned}\)
Ck:\(7 \times 7 = 49\)\(\rightarrow\) 4 ¡Incorrecto!
Explicación: Para verificar, multiplica las raíces digitales de los números que estás multiplicando (\(7 \times 7 = 49\)); luego encuentra la raíz digital de 49 (4). Esto debe ser igual a la raíz digital del producto, 2136 (3). Como no lo hace, hay un error. Por lo tanto, el problema de multiplicación se hizo incorrectamente.
Alguien hizo los siguientes problemas de multiplicación, pero solo anotó las respuestas. Consulta la respuesta a cada problema mediante el uso de raíces digitales. ¡Muestra el trabajo!
| a.\(\begin{aligned} 74 \\ \underline{\times 53} \\ 3922 \end{aligned}\) | b.\(\begin{aligned} 29 \\ \underline{\times 36} \\ 944 \end{aligned}\) | c.\(\begin{aligned} 68 \\ \underline{\times 28} \\ 1904 \end{aligned}\) |
| d.\(\begin{aligned} 65 \\ \underline{\times 79} \\ 5125 \end{aligned}\) | e.\(\begin{aligned} 81 \\ \underline{\times 55} \\ 4455 \end{aligned}\) | f.\(\begin{aligned} 48 \\ \underline{\times 52} \\ 2596 \end{aligned}\) |
| g.\(\begin{aligned} 569 \\ \underline{\times 61} \\ 34709 \end{aligned}\) | h.\(\begin{aligned} 653 \\ \underline{\times 524} \\ 242172 \end{aligned}\) | i.\(\begin{aligned} 2333 \\ \underline{\times 1203} \\ 2806599 \end{aligned}\) |
Agrega o multiplica lo siguiente como se indica, luego usa raíces digitales para verificar la respuesta a cada problema. ¡Muestra el trabajo!
| a.\(\begin{aligned} 7362 \\ \underline{+ 5732} \end{aligned}\) | b.\(\begin{aligned} 8308 \\ \underline{ + 956} \end{aligned}\) |
| d.\(\begin{aligned} 6784 \\ \underline{ + 6835} \end{aligned}\) | e.\(\begin{aligned} 9994 \\ \underline{ + 8721} \end{aligned}\) |
| f.\(\begin{aligned} 57 \\ \underline{\times 8} \end{aligned}\) | g.\(\begin{aligned} 34 \\ \underline{\times 7} \end{aligned}\) |
| g.\(\begin{aligned} 87 \\ \underline{\times 52} \end{aligned}\) | h.\(\begin{aligned} 825 \\ \underline{\times 13} \end{aligned}\) |
El uso de Raíces Digitales es Verificar Problemas de Resta.
Para verificar la resta, normalmente se suma la diferencia (la respuesta) al sustraendo (el número que se le restó) y se ve si obtiene el minuendo (el número del que le restó). Es decir, para comprobar que 215 — 134 = 81 se hizo correctamente, simplemente agregue 81 y 134, que es 215. Para verificar la resta usando raíces digitales, simplemente agregue la raíz digital de la diferencia a la raíz digital del sustraendo y vea si obtiene la raíz digital del minuendo. Para comprobar que 215 — 134 = 81 se hizo correctamente, basta con agregar las raíces digitales 81 y 134:0 + 8 = 8. Verificar que 8 sea la raíz digital del minuendo, 215. ¡Lo es! Aquí hay otro ejemplo. Digamos que alguien hizo el siguiente problema de resta: 5462 — 2873 = 2589. Para verificar, agregue las raíces digitales de 2589 y 2873, o 6 + 2 para obtener 8. Dado que 8 es también la raíz digital de 5462, la respuesta probablemente sea correcta.
Aquí hay algunos ejemplos más de cómo verificar la resta usando raíces digitales.
\(\begin{aligned} 7362 & \rightarrow 0 \\ \underline{ – 5732} & \rightarrow 8 \\ 1630 & \rightarrow 1 \end{aligned}\)
Ck: 1 + 8 = 9\(\rightarrow\) 0 ¡\(\surd\)Correcto!
Explicación: Para verificar, agregar la raíz digital de la diferencia y restar (1 + 8 = 9). La raíz digital de 9 es 0. Verificar que esto sea igual a la raíz digital del minuendo, 7632 (0). Como lo hace, la resta probablemente se hizo correctamente.
\(\begin{aligned} 5073 & \rightarrow 6 \\ \underline{ – 878} & \rightarrow 5 \\ 4205 & \rightarrow 2 \end{aligned}\)
Ck: 2 + 5 = 7 ¡INCORRECTO!
Explicación: Para verificar, agregar la raíz digital de la diferencia y restar (2 + 5 = 7). Esto debería igualar la raíz digital del minuendo, 5073 (6). Como no lo hace, la resta no se hizo correctamente.
Alguien hizo los siguientes problemas de sustracciones, pero solo anotó las respuestas. Consulta la respuesta a cada problema mediante el uso de raíces digitales. ¡Muestra el trabajo!
| a.\(\begin{aligned} 572 \\ \underline{– 356} \\ 216 \end{aligned}\) | b.\(\begin{aligned} 296 \\ \underline{– 189} \\ 107 \end{aligned}\) | c.\(\begin{aligned} 501 \\ \underline{– 327} \\ 284 \end{aligned}\) |
| d.\(\begin{aligned} 3217 \\ \underline{– 2391} \\ 926 \end{aligned}\) | e.\(\begin{aligned} 3546 \\ \underline{– 1138} \\ 2408 \end{aligned}\) | f.\(\begin{aligned} 7502 \\ \underline{– 4729} \\ 2773 \end{aligned}\) |
Resta, suma o multiplica lo siguiente como se indica, luego usa raíces digitales para verificar la respuesta a cada problema. ¡Muestra el trabajo!
| a.\(\begin{aligned} 7362 \\ \underline{– 5732} \end{aligned}\) | b.\(\begin{aligned} 8308 \\ \underline{– 956} \end{aligned}\) |
| d.\(\begin{aligned} 6784 \\ \underline{– 6335} \end{aligned}\) | e.\(\begin{aligned} 9994 \\ \underline{– 8721} \end{aligned}\) |
| f.\(\begin{aligned} 557 \\ \underline{+ 348} \end{aligned}\) | g.\(\begin{aligned} 834 \\ \underline{+ 767} \end{aligned}\) |
| h.\(\begin{aligned} 48 \\ \underline{\times 6} \end{aligned}\) | i.\(\begin{aligned} 13 \\ \underline{\times 29} \end{aligned}\) |
El uso de Raíces Digitales es Verificar Problemas de División.
Para verificar la división, multiplicas el divisor (el número por el que estás dividiendo) por el cociente (la respuesta), y luego agregas el resto. Es correcto si la respuesta obtenida es igual al dividendo (el número en el que dividiste). En otras palabras, aquí es cómo verificar esta división,\(431 \div 34 = 12\) r. 23: Multiplica 34 por 12 y agrega 23. Aquí están los pasos:\(34 \times 12 + 23 = 408 + 23 = 431\). Ya que 431 es el dividendo, este problema se hizo correctamente. Para verificar la división usando raíces digitales, simplemente multiplique la raíz digital del divisor por la raíz digital del cociente, y agregue la raíz digital del resto. Si la raíz digital de ese número es igual a la raíz digital del dividendo, probablemente sea correcta.
Nota: Después de multiplicar las raíces digitales del divisor y el cociente, primero puede encontrar la raíz digital de ese producto antes de agregar la raíz digital del resto.
Aquí se explica cómo verificar el problema de división que hicimos anteriormente mediante el uso de raíces digitales. Multiplicar la raíz digital del divisor, 34, por la raíz digital del cociente, 12:\(7 \times 3 = 21\). Después agrega la raíz digital del resto, 23:21 + 5 = 26. Determinar la raíz digital de ese número, 26, que es 8. Comprueba si 8 coincide con la raíz digital del dividendo, 431. Lo hace. Como se indica en la nota, se podría determinar la raíz digital de 21 antes de agregar la raíz digital del resto. En este caso, se habría visto así:\(7 \times 3 = 21 \rightarrow 3\). Después agrega la raíz digital del resto, 23:3 + 5 = 8. Verificar que esto sea igual a la raíz digital del dividendo, 431. Lo hace. Por lo tanto, la división probablemente se hizo correctamente. Siguen más ejemplos. El cheque sin raíces digitales se muestra a la derecha. La comprobación raíz digital se muestra bajo el problema de división.

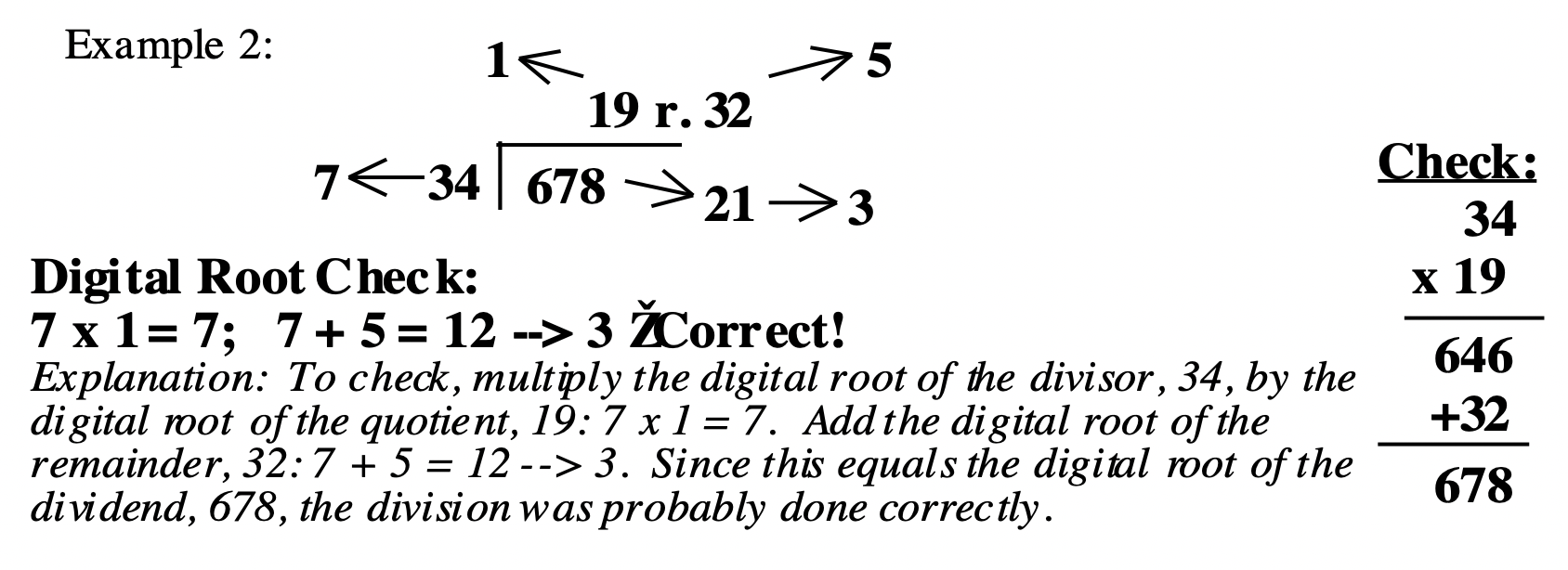
A continuación se muestra un ejemplo más para que estudies.

Alguien hizo los siguientes problemas de división, pero solo anotó las respuestas. Consulta la respuesta a cada problema mediante el uso de raíces digitales. Mostrar trabajo. No es necesario hacer la comprobación real como se muestra a la derecha de los tres últimos ejemplos. ¡Mostrar trabajo!
|
a. 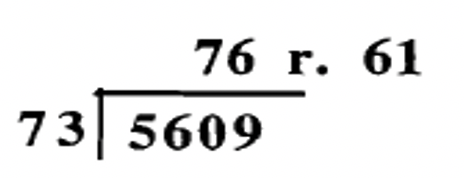 |
b. 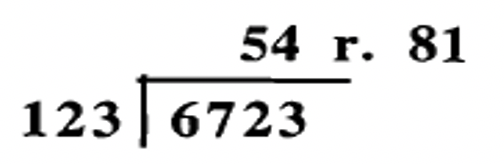 |
|
c. 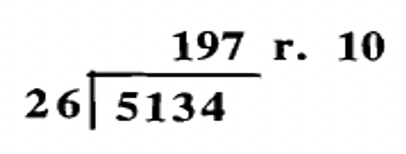 |
d. 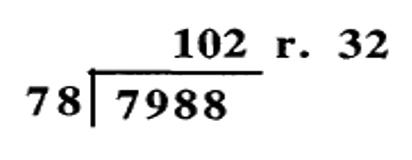 |
Una nota más de precaución sobre el uso de raíces digitales:
En el problema 9d, un error común que algunas personas cometen es olvidar poner el cero en el cociente, 102. En cambio, la respuesta podría haberse escrito como 12 r. 32. Usando raíces digitales, la respuesta verificaría. Entonces, también debes verificar la razonabilidad de la respuesta aproximando. Por ejemplo,\(78 \times 12\) es alrededor de 80 veces 10 u 800, lo que ni siquiera está cerca de igualar el dividendo, 7988. Otra vez que las raíces digitales podrían fallar es cuando alguien transpone los dígitos de un número. Si la respuesta a un problema era 465, y se escribía como 456, el uso de raíces digitales no detectaría el error.
Haga el siguiente problema de división, y verifique la respuesta usando raíces digitales. Mostrar trabajo.
\(23972 \div 156\)= ____________
Más adelante en este módulo, exploraremos los números primos, los números compuestos, el mayor factor común de dos o más números, y el múltiplo menos común de dos o más números. Factorización es el método utilizado para encontrar la factorización primo de un número compuesto, y también se puede utilizar para encontrar el mayor factor común y el mínimo común múltiplo de un conjunto de números. Uno de los problemas en la factorización de grandes números es que a veces no está claro si es primo o compuesto. En otras palabras, no está claro si tiene algún factor distinto al 1 o a sí mismo. La mayoría de nosotros sabemos que si el último dígito de un número es par, entonces 2 se dividirá en él; o si termina en 0, 10 se dividirá en él; o si termina en 0 o 5, ese 5 dividirá en él. A veces, las personas incluso tienen problemas para determinar si los números relativamente pequeños son primos. Por ejemplo, mucha gente piensa que 91 es prime, pero de hecho no lo es. Conocer algunas pruebas de divisibilidad facilita la tarea, por lo que pronto nos tomaremos un tiempo para discutir las pruebas de divisibilidad para varios números. Primero, tenemos que repasar alguna notación referente a la divisibilidad.
Cuando veas 12/3, esto significa 12 "dividido por" 3. El corte que se inclina hacia la derecha es otra forma de escribir el letrero de división,\(\div\). 12/3 (o\(12 \div 3\)) es un problema de división, y la respuesta es 4.
Aquí hay algo completamente diferente. Si digo “3 divide 12", estoy haciendo una declaración. “3 divide 12" no es un problema de división que deba hacerse. Es una afirmación que pasa a ser cierta. El símbolo utilizado para representar la palabra “divide” es una línea vertical. Entonces, “3 divide 12" se puede escribir “3|12". Nuevamente, esto es una declaración, un hecho, no un problema de división. La forma de expresar “no divide” es poner una barra a través del símbolo:\(\not{l}\)
Entonces, ¿cómo sé que “3 divide 12" es una afirmación verdadera? La definición de “divide” sigue:
Definición: “a divide b” si existe un número entero, n, tal que an = b ¡Esto es simplemente decir que “a divide b” significa a es un factor de b! En notación abreviada, esto se escribe “a | b si existe un número entero, n, tal que an = b, o a | b significa que a es un factor de b”.
Bien, entonces, ¿qué significa exactamente “existe un número entero, n, tal que an = b” significa? Bueno, significa que el primer número multiplicado por algún número entero equivale al segundo número. O se puede pensar que “a divide b” es cierto si\(b \div a\) es un número entero.
Volvamos a por qué “3 divide 12" es una verdadera declaración. Hmmm... puedes ser formal y preguntarte: ¿Hay un número entero n tal que 3n = 12? O, simplemente puedes preguntarte: ¿3 es un factor (o divisor) de 12? En cualquier caso, la respuesta es sí, por lo que la afirmación es cierta.
Trabajemos un poco más en la diferencia entre una declaración usando “divide”, y un problema de división real.
Ejemplos: Determinar si cada uno de los siguientes es una declaración o si es un problema de división. Si se trata de una declaración, indica si es verdadera o falsa y respalda tu respuesta. Si se trata de un problema de división, exponer la respuesta al problema de división.
4|20
Solución
Esta es una afirmación verdadera, porque 4 es un factor de 20 (ya que\(4 \cdot 5 = 20\))
20/6
Solución
Esto es un problema de división. La respuesta es 3 r. 2
15|3
Solución
Esta es una declaración falsa porque 15 no es un factor de 3
6 divide 20
Solución
Esta es una declaración falsa porque 6 no es un factor de 20
3 divide 21
Solución
Esta es una afirmación verdadera porque 3 es un factor de 21 (ya que\(3 \cdot 7 = 21\))
Determinar si cada uno de los siguientes es una declaración o si se trata de un problema de división. Si se trata de una declaración, entonces decide si es verdadera o falsa y respalde tu respuesta. Si se trata de un problema de división, exponer la respuesta al problema de división. Estudia los ejemplos de la página anterior si necesitas ayuda para comenzar.
| a. 35/7 |
| b. 35|7 |
| c. 7|35: |
| d. 40/7 |
| e. 56|8 |
| f. 7|40: |
| g. 12 divide 60 |
| h. 80 dividido por 30 |
| i. 70 dividido por 5 |
| j. 42 divide 3 |
| k. 6 divide 42 |
| l. 80 dividido por 10 |
| m. 100/2 |
| n. 4|100 |
| o. 4|90: |
| p. 25|5 |
Volvamos a la definición formal de “divide”:
Definición: a|b si existe un número entero, n, tal que an = b.
Necesitamos usar esta notación formal para poder hacer algunas pruebas. Considera lo siguiente:
¿Es cierta la siguiente afirmación? Si a|b y a|c, entonces a| (b+c).
a|b y a|c significa que a es un factor de b y a es también un factor de c. Debemos determinar si eso implica necesariamente que a es también un factor de la suma, b + c. La primera línea de estrategia es probarla en unos pocos números, y ver si se puede encontrar un contraejemplo. Si encuentras un contraejemplo, la respuesta es no y ya terminaste. Si no encuentras un contraejemplo, a lo mejor es cierto. Si crees que es cierto, debes PROBARLO siendo general y formal.
Comenzaría escogiendo cualquier número para a, como a = 3, y luego elegiría números para b y c para los cuales 3 es un factor, como 15 y 18. Conéctelos: “Si 3|15 y 3|18, ¿3| (15+18)?” Desde 3|33, la respuesta es sí. Parece que esta afirmación podría ser cierta.
Elija diferentes números para a, b y c en “Si a|b y a|c, entonces a| (b+c)” para ver si la afirmación parece ser verdadera.
La afirmación, “Si a|b y a|c, entonces a| (b+c)”, pasa a ser cierta. Debes escribir un comprobante para demostrar que siempre es cierto. Aquí hay una manera de escribir una prueba formal:
¿Es cierta la siguiente afirmación? : Si a|b y a|c, entonces a| (b+c).
Solución
Si a|b, entonces an = b para algún número entero, n. Si a|c, entonces am = c para algún número entero, m. Usando estas sustituciones para b y c, obtenemos que a| (b + c) es verdadero si a| (an + am) que es cierto si a es un factor de un + am. Factor: an + am = a (n + m). Esto demuestra claramente que a es efectivamente un factor de una + am. Por lo tanto, si a|b y a|c, entonces a| (b+c).
Escriba una prueba formal para demostrar que lo siguiente es cierto: Si x|y y x|z, entonces x| (y + z).
¿Es cierta la siguiente afirmación? Si a| (b+c), entonces a|b y a|c.
a| (b + c) significa que a es un factor de la suma, b + c. La pregunta pregunta si eso implica necesariamente que a es un factor de b y también un factor de c. La primera línea de estrategia es probarla en unos pocos números, y ver si puedes encontrar un contraejemplo, o si parece que es cierto. Si encuentras un contraejemplo, la respuesta es no y ya terminaste. Si crees que es cierto, debes PROBARLO siendo general y formal.
Comienza escogiendo cualquier número para a, como a = 3 y escogiendo un número para la suma b + c, para lo cual 3 es un factor, como 15 o 18, etc. Vamos b + c = 15. Tenga en cuenta que hay muchas combinaciones de números que suman 15:1 + 14, 2 + 13, 3 + 12, 7 + 8, etc. Se le está preguntando si 3 divide en la suma de dos números enteros cualesquiera, ¿necesariamente se dividirá también en cada adenda individual? Por ejemplo, si rompiste 15 como la suma de 9 y 6, esta sería la declaración: “Si 3| (9 + 6), entonces 3|9 y 3|6”. Usando estos números, es cierto y no has encontrado un contraejemplo. Intenta dividir 15 de otra manera, tal vez como la suma de 10 y 5. Entonces, el enunciado se convierte en: “Si 3| (10 + 5), entonces 3|10 y 3|5”. La respuesta es no, y por lo tanto estos números pueden ser utilizados como contraejemplo, lo que demuestra que la afirmación es falsa. Recuerde: Para que una declaración sea cierta, debe ser para todos los valores de a y b. Por otra parte, sólo un contraejemplo que muestre que no es cierto es suficiente para probar que una declaración es falsa.
Considera la afirmación: “Si a| (b+c), entonces a|b y a|c”. Proporcione un ejemplo usando números distintos a a = 3, b = 9 y c = 6 que haga que parezca que esta afirmación podría ser cierta.
Considera la afirmación: “Si a| (b+c), entonces a|b y a|c”. Proporcione un contraejemplo usando números distintos de a = 3, b = 10 y c = 5 para mostrar que esta declaración es falsa.
Considera la afirmación: “Si a|c y b|c, entonces (a + b) |c.” Proporcionar un contraejemplo para mostrar que esta declaración es falsa.
Considera la afirmación: “Si (a + b) |c, entonces a|c y b|c”. Proporcionar un contraejemplo para mostrar que esta declaración es falsa.
Demostrar que la siguiente afirmación es cierta: “Si a|b y a|c, entonces a| (bc)”
Demostrar que la siguiente afirmación es cierta: “Si a|b y a| (b + c), entonces a|c”
Solución
Si a|b, entonces am = b para algún número entero, m. Si a| (b + c), entonces an = b + c para algún número entero, n. Tenga en cuenta que como b y c son positivos, entonces (b + c) > b, que significa n > m. Estamos tratando de demostrar que a es un factor de c. Puesto que am = b, podemos sustituir am por b en la ecuación an = b + c, que significa an = am + c. Resolviendo para c, esto equivale a an — am = c. Entonces, si a es un factor de an — am, entonces a es un factor de c. Factor: an — am = a (n — m). Esto muestra claramente que a es un factor de an — am, lo que significa que a es un factor de c. Por lo tanto, la afirmación “Si a|b y a| (b + c), entonces a|c” es verdadera. (Nota: n — m debe ser un número entero ya que n y m son números enteros y n > m.)
Demostrar que la siguiente afirmación es verdadera: “Si c|a y c| (a + b), entonces c|b”
Bien, finalmente a las pruebas de divisibilidad. Usaremos nuestra nueva notación para divides (|).
Todos los números de conteo pueden considerarse factores de cero. En otras palabras, para todos los números de conteo, m, m|0 siempre es cierto ya que siempre hay algún número por m que es igual a cero, es decir, el cero mismo.
Supongamos que n es un número entero positivo. Las siguientes son pruebas de divisibilidad para determinar qué números se dividen en n, o qué números son factores de n.
Prueba de divisibilidad para 2:2|n si el último dígito de n es par (0, 2, 4, 6 u 8)
Utilice la prueba de divisibilidad para 2 para determinar si lo siguiente es verdadero o falso
1. 2|97
Esto es falso porque el último dígito (7) no es par
2. 2|356
Esto es cierto porque el último dígito (6) es par
Prueba de divisibilidad para 4: (piense en 4 como\(2^{\mathbf{2}}\))
4|n si 4| (el número representado por los dos últimos dígitos de n)
Utilice la prueba de divisibilidad para 4 para determinar si lo siguiente es verdadero o falso.
1. 4|527
Esto es falso porque 4 no divide 27, (ya que 4 no es un factor de 27).
2. 4|25,356
Esto es cierto porque 4|56.
3. 4|624
Esto es cierto porque 4|24.
Prueba de divisibilidad para 8: (piense en 8 como\(2^{\mathbf{3}}\))
8|n si 8| (el número representado por los últimos tres dígitos de n)
Utilice la prueba de divisibilidad para 8 para determinar si lo siguiente es verdadero o falso.
1. 8|42,527
Esto es falso porque 8 no divide 527
2. 8|25,336
Esto es cierto porque 8|336
3. 8|7,624
Esto es cierto porque 8 sí divide 624, (ya que 8 es un factor de 624)
Te debe quedar claro que si un número no es divisible por 2, no es divisible por 4 o 8; y si no es divisible por 4, no es divisible por 8. A la inversa, si un número es divisible por 8, entonces es divisible por 2 y 4; y si es divisible por 4, es divisible por 2.
Utilice las pruebas de divisibilidad para 2, 4 y 8 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad adecuada.
| a. 2|9,712 _____ |
| b. 2|5,643 _____ |
| c. 4|5,690 _____ |
| d. 4|63,868 _____ |
| e. 4|854.100 _____ |
| f. 8|12,345,248 _____ |
| g. 8| 54,094,422 _____ |
Prueba de divisibilidad para 5:5|n si el último dígito de n es 0 o 5
Utilice la prueba de divisibilidad para 5 para determinar si lo siguiente es verdadero o falso.
1. 5|527
Esto es falso porque 7 es el último dígito de 527
2. 5|25,335
Esto es cierto porque 5 es el último dígito de 25,335
3. 5|7,620
Esto es cierto porque 0 es el último dígito de 7,620
Prueba de divisibilidad para 10:10|n si el último dígito de n es 0
Utilice la prueba de divisibilidad para 10 para determinar si lo siguiente es verdadero o falso.
1. 10|527
Esto es falso porque 7 es el último dígito de 527
2. 10|25,335
Esto es falso porque 5 es el último dígito de 25,335
3. 10|7,620
Esto es cierto porque 0 es el último dígito de 7,620
Utilice las pruebas de divisibilidad para 5 y 10 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad adecuada.
| a. 5|9,750 _____ |
| b. 5|5,645 _____ |
| c. 5|5,696 _____ |
| d. 10|63,860 _____ |
| e. 10|854,105 _____ |
Prueba de divisibilidad para 3:3|n si 3| (la raíz digital de n)
Nota: Esto equivale a decir 3|n si la raíz digital de n es 0, 3 o 6
Utilice la prueba de divisibilidad para 3 para determinar si lo siguiente es verdadero o falso.
1. 3|97
Esto es falso porque 3 no divide 7, que es la raíz digital de 97
2. 3|356
Esto es falso porque 3 no divide 5, que es la raíz digital del 356
3. 3|738
Esto es cierto porque 3|0, donde 0 es la raíz digital de 738
Utilice la prueba de divisibilidad para 3 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 3. Mostrar trabajo.
| a. 3|9,750 ______ |
| b. 3|5,645 ______ |
| c. 3|5,696 ______ |
| d. 3|63,860 ______ |
| e. 3|854.115 ______ |
Prueba de divisibilidad para 9:9|n si 9| (la raíz digital de n)
Nota: Esto equivale a decir que la raíz digital de n debe ser igual a cero. Tómate un momento para pensar en esta prueba de divisibilidad para 9. En el ejercicio 16, descubrimos que la raíz digital de un número es la misma que el resto que obtienes cuando divides un número por 9. Para que un número sea divisible por 9, el resto sería cero, que es exactamente lo que sería la raíz digital.
Utilice la prueba de divisibilidad para 9 para determinar si lo siguiente es verdadero o falso.
1. 9|627
Esto es falso porque 9 no divide 6, que es la raíz digital de 627.
2. 9|25,334
Esto es falso ya que 9 no divide 8, que es la raíz digital de 25,334.
3. 9|7,533
Esto es cierto porque la raíz digital de 9 es 0.
Utilice la prueba de divisibilidad para 9 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 9. Mostrar trabajo.
| a. 9|9,753 ______ |
| b. 9|5,646 ______ |
| c. 9|5,697 ______ |
| d. 9|63,576 ______ |
| e. 9|854,103 ______ |
Prueba de divisibilidad para 6:6|n si 2|n Y 3|n. (Piense en 6 como\(2 \cdot 3\))
Nota Importante: Un número es divisible por 6 solo si pasa la prueba de divisibilidad tanto para 2 como para 3. Si no pasa una de las pruebas, entonces no es divisible por 6. Para mostrar que es divisible por 6, debes demostrar que pasa ambas pruebas.
Utilice la prueba de divisibilidad para 6 para determinar si lo siguiente es verdadero o falso.
1. 6|627
Esto es falso porque 2 no divide 7 (el último dígito, que no es par).
2. 6|25,334
Esto es falso porque 3 no divide 25,334, ya que 3 no divide la raíz digital, que es 8.
3. 6|7,620
Esto es cierto porque 2|7,620 (desde el último dígito, 0, es par) Y 3|7,620 (desde 3|6, donde 6 es la raíz digital de 7,620).
Utilice la prueba de divisibilidad para 6 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 6.
| a. 6|9,753 |
| b. 6|5,645 |
| c. 6|5,696 |
| d. 6|63,876 |
| e. 6|854,103 |
Prueba de divisibilidad para 15:15|n si 5|n Y 3|n. (Piense en 15 como\(5 \cdot 3\))
Nota Importante: Un número es divisible por 15 solo si pasa la prueba de divisibilidad tanto para 5 como para 3. Si no pasa una de las pruebas, entonces no es divisible por 15. Para mostrar que es divisible por 15, debes demostrar que pasa ambas pruebas.
Utilice la prueba de divisibilidad para 15 para determinar si lo siguiente es verdadero o falso.
1. 15|623: Esto es falso porque 5 no divide 623 (ya que el último dígito no es 0 o 5).
2. 15|24,335: Esto es falso porque 3 no divide 24,335, ya que 3 no divide la raíz digital, que es 8.
3. 15|7,620: Esto es cierto porque 5|7,620 (ya que el último dígito es 0) Y 3|7,620 (desde 3|6, donde 6 es la raíz digital de 7,620).
Utilice la prueba de divisibilidad para 15 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 15.
| a. 15|9.753 |
| b. 15|6,645 |
| c. 15|5,690 |
| d. 15|63,872 |
| e. 15|654,105 |
Prueba de divisibilidad para 7 : Esta prueba no es fácil de describir. A continuación se presentan los pasos.
Paso 1: Tocar el dígito del número para obtener un número con un valor posicional menos.
Paso 2: Duplica el dígito que tachaste y resta del nuevo número obtenido al faltar el dígito de uno.
Paso 3: Si 7 divide el número que obtienes después de restar, divide el número original. De lo contrario, no lo hace. Si no está seguro, repita el procedimiento en el nuevo número volviendo al paso 1.
Utilice la prueba de divisibilidad para 7 para determinar si lo siguiente es verdadero o falso. La forma en que mostrarías los pasos usando los números se muestra a la derecha de la explicación.
|
1. 7|91: Tachar el 1, duplicarlo (2), y restar de lo que queda (9). La respuesta es 7 (9 — 2 = 7). Desde 7|7, 7|91 es cierto. 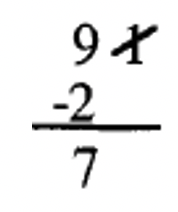 |
|
2. 7|96: Tachar el 6, duplicarlo (12), y restar de lo que queda (9). Cuando restes, ignora el signo (solo haz 12 — 9 = 3). Dado que 7 no divide 3, 7|96 es falso. 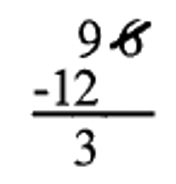 |
|
3. 7|638: Tachar el 8, duplicarlo (16) y restar de lo que queda (63). La respuesta es 47 (63 — 16 = 47). Ya que 7 no divide 47, entonces 7|638 es falso. (Si no estabas seguro de si 7 dividido o no 47, puedes llevarlo un paso más allá; esto se muestra a la derecha). 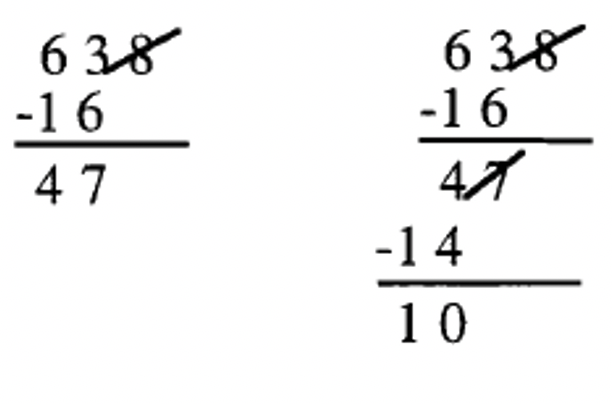 |
|
4. 7|4564: Tocar el 4, doblarlo (8) y restar de lo que queda (456). La respuesta es 448 (456 — 8 = 456). Tocar el 8, doblarlo (16) y restar de lo que queda (44). La respuesta es 28 (44 — 16 = 28). Desde 7|28, entonces 7|4564 es cierto. 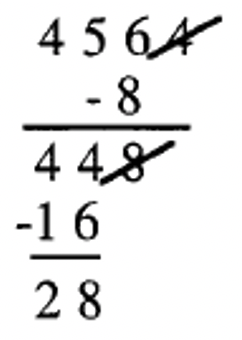 |
|
5. 7|56161: Tocar el 1, duplicarlo (2) y restar de lo que queda (5616 — 2 = 5614). Tachar el 4, duplicarlo (8) y restarlo de lo que queda (561 — 8 = 553). Tachar el 3, duplicarlo (6) y restar de lo que queda (55 — 6 = 49). Desde 7|49, entonces 7|56161 es cierto. 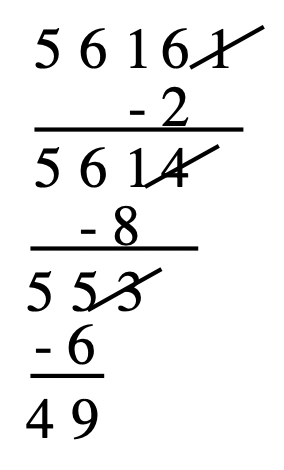 |
Utilice la prueba de divisibilidad para 7 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 7. Mostrar trabajo.
| a. 7|833 |
| b. 7|5,645 |
| c. 7|4,795 |
| d. 7|14,763 |
Prueba de divisibilidad para 11:11|n si la diferencia entre la suma de los dígitos en los lugares que son potencias pares de 10 y la suma de los dígitos en los lugares que son potencias impares de 10 es divisible por 11.
Esta prueba es más confusa de describir que de hacer. Lo que haces es sumar cada dos dígitos. Entonces, suma los que te salteaste. Entonces, restar estos dos números y ver si 11 divide este número.
Utilice la prueba de divisibilidad para 11 para determinar si lo siguiente es verdadero o falso.
a. 11|4,365: Sumar 4 + 6 = 10 Sumar 3 + 5 = 8 Restar 10 — 8 = 2 Ya que 11 no divide 2, entonces 11 no divide 4365. Por lo tanto, 11|4365 es falso.
b. 11|540,879,216: Sumar 5 + 0 + 7 + 2 + 6 = 20. Agregar 4 + 8 + 9 + 1 = 22. Restar 22 — 20 = 2 Dado que 11 no divide 2, 11|540,879,216 es falso.
c. 11|542,879,216: Suma 5 + 2 + 7 + 2 + 6 = 22 Sumar 4 + 8 + 9 + 1 = 22 Restar 22 — 22 = 0 Desde 11|0, entonces 11|542,879,216 es cierto.
d. 11|4,052,631: Suma 4 + 5 + 6 + 1 = 16 Sumar 0 + 2 + 3 = 5 Restar 16 — 5 = 11 Desde 11|11, entonces 11|4,052,631 es cierto.
Utilice la prueba de divisibilidad para 11 para determinar si lo siguiente es verdadero o falso. Apoye tu respuesta con una razón usando la prueba de divisibilidad para 11. Mostrar trabajo.
| a. 11|9,053 |
| b. 11|63,920,876 |
| c. 11|568,696 |
| d. 11|513,645 |
| e. 11|803,003,808 |
A continuación se enumeran las pruebas de divisibilidad que debes conocer. Es importante darse cuenta de que cada una de las pruebas sólo funciona para el número especificado. En otras palabras, no se puede usar la prueba de divisibilidad para 3 para determinar si 7 divide un número. ¡La prueba de divisibilidad para 7 no tiene nada que ver con raíces digitales!
Prueba de divisibilidad para 2:2|n si el último dígito de n es par (0, 2, 4, 6 u 8)
Prueba de divisibilidad para 3:3|n si 3| (la raíz digital de n); O 3|n si la raíz digital de n es 0, 3 o 6
Prueba de divisibilidad para 4:4|n si 4| (el número representado por los dos últimos dígitos de n)
Prueba de divisibilidad para 5:5|n si el último dígito de n es 0 o 5
Prueba de divisibilidad para 6:6|n si 2|n Y 3|n. (Piense en 6 como\(2 \cdot 3\))
Prueba de Divisibilidad para 7: A continuación se describen los pasos de esta prueba.
- Paso 1: Tocar el dígito del número para obtener un número con un valor posicional menos.
- Paso 2: Duplica el dígito que tachaste y resta del nuevo número sin el dígito del uno.
- Paso 3: Si 7 divide el número que obtienes después de restar, divide el número original. De lo contrario, no lo hace. Si no está seguro, repita el procedimiento en el nuevo número volviendo al paso 1.
Prueba de divisibilidad para 8:8|n si 8| (el número representado por los últimos tres dígitos de n)
Prueba de divisibilidad para 9:9|n si 9| (la raíz digital de n); O 9|n si la raíz digital de n es cero
Prueba de divisibilidad para 10:10|n si el último dígito de n es 0
Prueba de divisibilidad para 11:11|n si la diferencia entre la suma de los dígitos en los lugares que son potencias pares de 10 y la suma de los dígitos en los lugares que son potencias impares de 10 es divisible por 11
Prueba de divisibilidad para 15:15|n si 5|n Y 3|n


