6.6: La serie armónica

El gran fundamento de las matemáticas es el principio de contradicción, o de identidad, es decir que una afirmación no puede ser verdadera y falsa al mismo tiempo, y que así A es A, y no puede ser no A. Y este principio único es suficiente para probar la totalidad de la aritmética y la totalidad de la geometría, es decir, todos los principios matemáticos.

Gottfried W. Leibniz (1646-1716)

Hemos visto como a algunas series infinitas, o sumas que siguen para siempre, se les puede asignar un valor finito para su suma:

$$1+r+r^2+r^3+\cdots (\text{para siempre})=\frac{1}{1-r}$$ $$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots +\frac{1}{n(n+1)}+\cdots (\text{para siempre})=1$$ $$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +$$1n2+⋯ (para siempre)=π26$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{para siempre})=e.$$

Decimos que estas series convergen (es decir, que se les puede asignar un valor finito).

Esta sección se refiere a otra serie muy natural, la llamada serie armónica

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots (\text{para siempre}).$$

No está del todo claro por qué a esto se le llama la serie armónica. Los armónicos naturales que surgen en relación con el desplume de una cuerda estirada (como con una guitarra o un arpa) tienen longitudes de onda que son$\genfrac{}{}{0.1ex}{}{1}{2}$la longitud de onda básica, o$\genfrac{}{}{0.1ex}{}{1}{3}$de la longitud de onda básica, y así sucesivamente. También es cierto que, así como cada término de una serie aritmética es la media aritmética de sus dos vecinos, y cada término de una serie geométrica es la media geométrica de sus dos vecinos, así cada término de la serie armónica después de la primera es igual a la media armónica (ver Problemas 85., 89.) de sus dos vecinos:

$$\frac{1}{k}=\frac{2}{{\left(\frac{1}{k-1}\right)}^{-1}+{\left(\frac{1}{k+1}\right)}^{-1}}.$$

A diferencia de las dos primeras series anteriores, no hay una fórmula cerrada obvia para la suma finita

$$s_n=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}.$$

Ciertamente la secuencia de sumas sucesivas

$$s_1=1,s_2=\frac{3}{2},s_3=\frac{11}{6},s_4=\frac{25}{12},s_5=\frac{137}{60},...$$

no sugiere ningún patrón general.

Problema 252 Supongamos que denotamos por S el “valor” de la suma sin fin

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(para siempre)}$$

(i) Escribir la suma interminable correspondiente a”$\frac{1}{2}S$”.

ii) Eliminar los términos de esta suma interminable de la suma interminable S, para obtener otra suma interminable correspondiente a”$S-\frac{1}{2}S$”$=$12S.

iii) Comparar el primer término de la serie del inciso i) (a saber,$\genfrac{}{}{0.1ex}{}{1}{2}$) con el primer término de la serie en (ii) (a saber, 1); comparar el segundo término de la serie en (i) con el segundo término de la serie en (ii); y así sucesivamente. ¿Qué notas?

La cita anterior de Leibniz enfatiza que la confiabilidad de las matemáticas deriva de un solo principio, a saber, la negativa a tolerar una contradicción. Ya hemos hecho uso explícito de este principio de vez en cuando (véase, por ejemplo, la solución al Problema 125.). El mensaje es simple: cada vez que golpeamos una contradicción, sabemos que nos hemos “equivocado” —ya sea cometiendo un error de cálculo o lógica, o comenzando con una suposición falsa. En Problema 252. las observaciones que se esperaba que hicieras son paradójicas: obtuviste dos series distintas, que ambas corresponden a”$\frac{1}{2}S$”, ¡pero cada término en una serie es mayor que el término correspondiente en la otra! Lo que se puede concluir puede no estar del todo claro. Pero ciertamente está claro que algo anda mal: de alguna manera hemos creado una contradicción. Los tres pasos (i), (ii), (iii)) parecen ser relativamente sensatos. Pero la observación final”$\frac{1}{2}S<\frac{1}{2}S$” (desde$\frac{1}{2}<1$,$\frac{1}{4}<\frac{1}{3}$, etc.) no tiene sentido. Y la única suposición obvia que hemos hecho es asumir que la suma interminable

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(para siempre)}$$

se le puede asignar un valor “S”, que luego se puede manipular como si se tratara de un número.

La conclusión parecería ser que, tenga o no sentido la suma interminable, no se le puede asignar un valor de esta manera. Decimos que la serie diverge. Cada suma finita

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}$$

tiene un valor, y estos valores “crecen cada vez más lentamente” a medida que n aumenta:

• el primer término inmediatamente hace que la suma = 1
• se necesitan 4 términos para obtener una suma > 2;
• se necesitan 11 términos para obtener una suma > 3; y
• se necesita$12367$términos antes de que la serie alcance una suma > 10.

Sin embargo, este lento crecimiento no es suficiente para garantizar que la suma interminable correspondiente corresponda a un valor numérico finito.

Las señales de peligro ya deberían haber sido evidentes en el Problema 249., donde demostró que

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}\ge \sqrt{n}$$

El$n^{\mathrm{th}}$término$\frac{1}{\sqrt{n}}$tiende a 0 a medida que n aumenta; así las sumas finitas crecen cada vez más lentamente a medida que n aumenta. Sin embargo, el LHS se puede hacer más grande que cualquier entero K simplemente tomando K ² términos. De ahí que no haya manera de asignar un valor finito a la suma sin fin

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}+\cdots (\text{para siempre}).$$

Problema 253.

a) i) Explicar por qué

$$\frac{1}{2}+\frac{1}{3}<1.$$ii) Explicar por qué$$$$

14+15+16+17<1.

$$\mathrm{<span\; style="display:\; none;"></span>}$$

$$$$

iii) Ampliar las partes i) y ii) para demostrar que$$$$

11+12+13+⋯+12n−1<n, para todos n≥2.

iv) Por último, utilizar el hecho de que, cuando$n\ge 3$,

$$\frac{}{}$$

12n<12−13

modificar ligeramente la prueba en (iii) y, por lo tanto, demostrar que$$\frac{1}{1}$$$$+\frac{1}{2}+\frac{1}{3}+\cdots +$$12n<n, para todos n≥3.

b) i) Explicar por qué

$$\frac{1}{3}+\frac{1}{4}>\frac{1}{2}.$$

ii) Explicar por qué

$$\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{2}.$$

iii) Ampliar las partes i) y ii) para demostrar que$$$$

11+12+13+⋯+12n>1+n2, para todos n≥2.

$$\mathrm{<span\; style="display:\; none;"></span>}$$

$$$$

(c) Combinar las partes (a) y (b) para demostrar que, para todos$n\ge 2$, tenemos las dos desigualdades$$$$

1+n2<11+12+13+⋯+12n<n.

$$<span\; style="display:\; none;"></span>$$

$$$$Concluye que la suma sin fin

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(para siempre)}$$

no se puede asignar un valor finito.

El resultado en Problema 253. c) tenga una consecuencia inesperada.

Problema 254 Imagina que tienes un suministro ilimitado de tiras rectangulares idénticas de longitud 2. (Estuches de plástico vacíos idénticos para CD pueden servir de ilustración útil, siempre que uno se centre en su perfil lateral rectangular, en lugar de la sección transversal frontal casi cuadrada). El objetivo es construir una 'pila' de tal manera que sobresalga lo más lejos posible más allá del borde de una mesa. Una tira se equilibra exactamente en su punto medio, por lo que puede sobresalir una distancia total de 1 sin volcarse.

(a) Organizar una pila de n tiras de longitud 2, una encima de la otra, con la tira inferior sobresaliendo a distancia$\frac{1}{n}$más allá del borde de la mesa, la segunda tira de la parte inferior sobresale$\frac{1}{n-1}$más allá del borde de ataque de la tira inferior, la tercera tira de la parte inferior sobresale$\frac{1}{n-2}$más allá del borde de ataque de la tira debajo de ella, y así sucesivamente hasta que el${(n-1)}^{\text{th}}$tira de la parte inferior sobresale distancia$\genfrac{}{}{0.1ex}{}{1}{2}$más allá del borde de ataque de la tira debajo de ella, y la tira superior sobresale la distancia 1 más allá del borde de ataque de la tira debajo de ella (ver Figura 10). Demostrar que una pila de n tiras idénticas dispuestas de esta manera solo evitará volcar sobre el borde de la mesa.

(b) Concluir que podemos elegir n para que una disposición de n tiras pueda (en teoría) sobresalir tanto más allá del borde de la mesa como queramos, sin volcar.

El siguiente problema ilustra, en el contexto de la serie armónica, lo que de hecho es un fenómeno completamente general: una suma interminable de términos positivos decrecientes de manera constante puede converger o divergir; pero siempre que los propios términos converjan a 0, luego los correspondientes “alternantes” sum” —donde se combinan los mismos términos pero con signos alternativamente positivos y negativos— siempre converge.

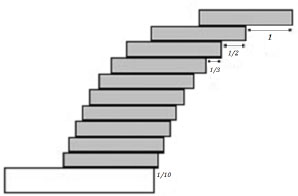
Figura 10: Tiras sobresalientes, n = 10.

Problema 255

(a) Dejar

$$s_n=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \pm \frac{1}{n}$$

(donde la operación final es “+” si n es impar y “-” si n es par).

i) Demostrar que

$$s_{2n-2}<$$s2n<s2m+1<s2m−1,para todos$m,n\ge 1$.

ii) Concluir que la suma alterna sin fin$$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \text{(para siempre)}$$

se le puede asignar un valor s que se encuentra en algún lugar entre$s_6=\frac{37}{60}$y$s_5=\frac{47}{60}$.

b) Dejar

$$a_1,a_2,a_3,...$$

ser una secuencia interminable y decreciente de términos positivos (es decir,$a_{n+1}<a_n$para todos$n\ge 1$). Supongamos que la secuencia de términos$a_n$converge a 0 como$n\to \infty$.

(i) Dejar

$$s_n=a_1-a_2+a_3-a_4+a_5-\cdots \pm a_n$$

(donde la operación final es “+” si n es impar y “−” si n es par). Demostrar que$$s_{2n-2}<s2n<s2m+1<s_{2m-1},\text{para todos}m,n\ge 1.$$

ii) Concluir que la suma alterna sin fin

$$a_1-a_2+a_3-a_4+a_5-\cdots \text{(para siempre)}$$

se le puede asignar un valor s que se encuentra en algún lugar entre$s_2=a_1-a_2$y$s_3=a_1-a_2+a_3$.

Al igual que con la serie

$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +1n^2+\cdots (\text{para siempre})$$$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{para siempre}),$$

podemos mostrar con relativa facilidad que

$$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots (\text{para siempre})$$

se le puede asignar un valor s. ¡Está mucho menos claro si este valor tiene un nombre familiar! (De hecho, es igual al logaritmo natural de 2:”${\mathrm{registro}}_{e}2$”.) Una serie igualmente intrigante es la serie alterna de términos impares de la serie armónica:$$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots (\text{para siempre})$$

Deberías poder demostrar que a esta serie interminable se le puede asignar un valor en algún lugar entre$s_2=\frac{2}{3}$y$s_3=\frac{13}{15}$; pero es muy poco probable que adivine que su valor es igual a$\frac{\pi }{4}$. Éste fue descubierto por primera vez en 1674 por Leibniz (1646-1716). Una forma de obtener el resultado es utilizar la integral de${(1+x^2)}^{-1}$de 0 a 1: por un lado la integral es igual a$$arctanxevaluado cuando$x=1$(es decir,$\frac{\pi }{4}$); por otro lado, podemos expandir el integrando como una serie de potencia$1-x^2+x^4-x^6+\cdots$, integrar término por término y demostrar que la serie resultante converge cuando$x=1$. (De hecho converge, aunque lo hace muy, muy lentamente).

El hecho de que la serie armónica alterna tenga el valor$$registroe2parece haber sido mostrado por primera vez por Euler (1707-1783), utilizando la expansión de la serie de potencia para$\mathrm{registro}(1+x)$.