16.5: Criptografía de Clave Pública
- Page ID
- 110454
Supongamos que se está conectando al sitio web de su banco. Es posible que alguien pueda interceptar cualquier comunicación entre usted y su banco, por lo que querrá cifrar la comunicación. El problema es que todos los métodos de cifrado que hemos discutido requieren que ambas partes ya hayan acordado una clave de cifrado secreta compartida. ¿Cómo pueden usted y su banco acordar una clave si aún no lo han hecho?
Esto se convierte en el objetivo de la criptografía de clave pública —proporcionar una forma para que dos partes acuerden una clave sin que un tercero fisgoneando pueda determinar la clave. El método se basa en una función unidireccional; algo que es fácil de hacer de una manera, pero difícil de revertir. Exploraremos el método de intercambio de claves Diffie-Hellman-Merkle.
Como ejemplo, consideremos mezclar pintura. Es fácil mezclar pintura para hacer un nuevo color, pero mucho más difícil separar una pintura mixta en los dos colores originales utilizados. [1] [2]
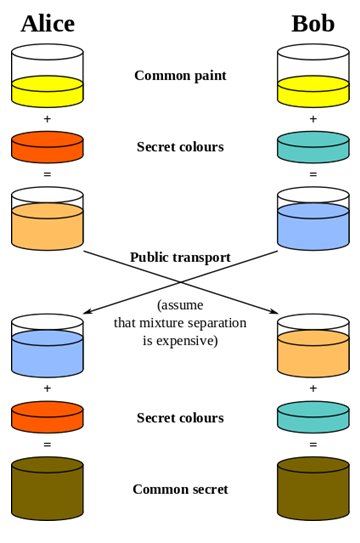Usando esta analogía, Alice y Bob coinciden públicamente en un color inicial común. Cada uno luego se mezcla en algo de su propio color secreto. Luego intercambian sus colores mezclados.
Dado que separar los colores es difícil, aunque un fisgón obtuviera estos colores mezclados, sería difícil obtener los colores secretos originales.
Una vez que han intercambiado sus colores mezclados, Alice y Bob agregan su color secreto a la mezcla que obtuvieron de la otra persona. Al hacerlo, tanto Alice como Bob tienen ahora el mismo color secreto común, ya que contiene una mezcla del color común original, el color secreto de Alice y el color secreto de Bob.
Ahora tienen un color secreto común que pueden usar como su clave de cifrado, a pesar de que ni Alice ni Bob conocen el color secreto del otro.
De igual manera, no hay manera de que un fisgón obtenga el color secreto común sin separar uno de los colores mezclados.
Para que este proceso funcione para la comunicación por computadora, necesitamos que el proceso dé como resultado un número común compartido para que actúe como la clave de cifrado secreta común. Para ello, necesitamos una función numérica unidireccional.
Aritmética modular
Si piensas en hacer división con números enteros, tal vez recuerdes haber encontrado el resultado del número entero y el resto después de la división.
Módulo [3]
El módulo es otro nombre para el resto después de la división.
Por ejemplo, 17 mod 5 = 2, ya que si dividimos 17 por 5, obtenemos 3 con resto 2.
La aritmética modular a veces se llama aritmética de reloj, ya que los relojes analógicos se envuelven los tiempos pasados las 12, lo que significa que funcionan en un módulo de Si la manecilla horaria de un reloj actualmente apunta a 8, entonces en 5 horas apuntará a 1. Mientras que\(8+5 = 13\), el reloj gira después de las 12, por lo que todos los tiempos pueden considerarse como el módulo 12. Matemáticamente, 13 mod 12 = 1.
Computación: a) 10 mod 3 b) 15 mod 5 c)\(2^{7}\) mod 5
Solución
a) Ya que 10 dividido por 3 es 3 con resto 1,10 mod\(3=1\)
b) Ya que 15 dividido por 5 es 3 sin resto, 15 mod\(5=0\)
c)\(2^{7}=128.128\) dividir por 5 es 25 con resto\(3,\) así\(2^{7}\) mod\(5=3\)
Computación: a) 23 mod 7 b) 15 mod 7 c) 2034 mod 7
- Contestar
-
a) 2 b) 1 c) 4
Recordemos que cuando dividimos 17 por 5, podríamos representar el resultado como 3 resto 2, como el número mixto\(3\frac{2}{5}\), o como el decimal 3.4. Observe que el módulo, 2, es el mismo que el numerador de la parte fraccionaria del número mixto, y que la parte decimal 0.4 es equivalente a la fracción. Podemos usar estas conversiones para calcular el módulo de números no demasiado grandes en una calculadora estándar.
Para calcular\(a\) mod\(n\) en una calculadora estándar
- Dividir\(a\) por\(n\)
- Restar toda la parte de la cantidad resultante
- \(n\)Multiplicar por para obtener el módulo
Calcular 31345 mod 419
Solución
\(\begin{array}{ll} 31345 / 419=74.8090692 & \text{Now subtract 74 to get just the decimal remainder} \\ 74.8090692-74=0.8090692 & \text{Multiply this by 419 to get the modulus} \\ 0.8090692 \times 419=339 & \text{This tells us 0.8090692 was equivalent to }\frac{339}{419} \end{array}\)
En el texto anterior, sólo se anotó una porción del valor decimal. En la práctica, debes tratar de evitar anotar los pasos intermedios, y en su lugar permitir que tu calculadora retenga tantos valores decimales como pueda.
La función unidireccional
Cuando usas un número primo\(p\) como módulo, puedes encontrar un número especial llamado generador, de\(g,\) modo que\(g^{n}\) mod\(p\) dará como resultado todos los valores de 1 a\(p-1\)
\ (\ begin {array} {|l|l|l|}
\ hline n & 3^ {n} & 3^ {n}\ mathrm {mod} 7
\\\ hline 1 & 3 & 3
\\ hline 2 & 9 & 2
\\ hline 3 & 27 & 6\
\ hline 4 & 81 & 4\
\ hline 5 & 243 y 5\\
\ hline 6 & 729 & 1\\
\ hline
\ end {array}\)
En la tabla a la parte superior, observe que cuando damos valores\(n\) de 1 a\(6,\) sacamos todos los valores de 1 a\(6 .\) Esto significa que 3 es un generador cuando 7 es el módulo.
Esto nos da nuestra función unidireccional. Si bien es fácil calcular el valor de\(g^{n}\) mod\(p\) cuando sabemos\(n\), es difícil encontrar el exponente\(n\) para obtener un valor específico.
Por ejemplo, supongamos que usamos\(p=23\) y\(g=5 .\) si escojo\(n\) ser\(6,\) puedo calcular con bastante facilidad\(5^{6}\) mod\(23=15625\) mod\(23=8\)
Si alguien más te dijera\(5^{n} \bmod 23=7\), es mucho más difícil de encontrar\(n\). En este caso en particular, tendríamos que probar 22 valores diferentes para\(n\) hasta que encontráramos uno que funcionara; no se conoce una forma más fácil de encontrar que no\(n\) sea adivinar la fuerza bruta.
Si bien probar 22 valores no tardaría demasiado, cuando se usan en la práctica\(p\) se usan valores mucho mayores para, típicamente con más de 500 dígitos. Probar todas las posibilidades sería esencialmente imposible.
El intercambio de claves
Antes de que podamos comenzar el proceso de intercambio de claves, necesitamos un par de datos más importantes sobre la aritmética modular.
\(\left(a^{b} \bmod n\right)=(a \bmod n)^{b} \bmod n\)
Calcular\(12^{5}\) mod 7 usando la regla de exponenciación.
Solución
Evaluado directamente:\(12^{5}=248,832,\) so\(12^{5}\) mod\(7=248,823\) mod\(7=3\)
Usando la regla anterior,\(12^{5}\) mod\(7=(12 \bmod 7)^{5} \bmod 7=5^{5} \bmod 7=3125 \bmod 7=3\)
Quizás recuerdes una regla básica de exponente del álgebra:
\[\left(a^{b}\right)^{c}=a^{b c}=a^{c b}=\left(a^{c}\right)^{b} \nonumber \]
Por ejemplo:
\[64^{2}=\left(4^{3}\right)^{2}=4^{6}=\left(4^{2}\right)^{3}=16^{3} \nonumber \]
Podemos combinar la regla de exponenciación modular con la regla de exponente de álgebra para definir la regla de potencia de exponente modular.
\[\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{b c} \bmod n\right)=\left(a^{c} \bmod n\right)^{b} \bmod n \nonumber \]
Verifique la regla anterior si\(a=3, b=4, c=5,\) y\(n=7\)
Solución
\(\left(3^{4} \bmod 7\right)^{5} \bmod 7=(81 \bmod 7)^{5} \bmod 7=4^{5} \bmod 7=1024 \bmod 7=2\)
\(\left(3^{5} \bmod 7\right)^{4} \bmod 7=(243 \bmod 7)^{4} \bmod 7=5^{4} \bmod 7=625 \bmod 7=2,\)el mismo resultado.
Utilice la regla de exponente modular para calcular\(10000 \bmod 7,\) anotando\(10000=10^{4}\)
- Contestar
-
\(10000 \bmod 7=10^{4} \bmod 7=(10 \bmod 7)^{4} \bmod 7=3^{4} \bmod 7=81 \bmod 7=4\)
Esto nos proporciona la base para nuestro intercambio de claves. Si bien será más fácil de entender en el siguiente ejemplo, aquí está el proceso:
- Alice y Bob coinciden públicamente en valores un prime\(p\) y generador\(g\).
- Alice elige algún número secreto\(a,\) mientras Bob elige algún número secreto\(b\).
- Alice calcula\(A=g^{2} \bmod p\) y se lo envía a Bob.
- Bob calcula\(B=g^{b}\) mod\(p\) y se lo envía a Alice.
- Alice calcula\(B^{a} \bmod p,\) que es\(\left(g^{b} \bmod p\right)^{a} \bmod p\).
- Bob calcula\(A^{b} \bmod p,\) cual es\(\left(g^{a} \bmod p\right)^{b} \bmod p\).
La regla de potencia de exponente modular nos dice\(\left(g^{a} \bmod p\right)^{b} \bmod p=\left(g^{b} \bmod p\right)^{a} \bmod p,\) que Alice y Bob llegarán al mismo valor compartido para usar como clave, aunque ninguno conozca el número secreto del otro, y ningún intruso puede determinar este valor sabiendo solo\(g, p, A,\) y\(B\)
Alice y Bob comparten públicamente un generador y un módulo primo. En este caso, usaremos 3 como generador y 17 como primo.
Solución
\(\begin{array}{llll} & \textbf{Alice} & & \textbf{Bob} \\ \text{Alice and Bob publically} & g=3, p=17 & \text{Common info} & g=3, p=17 \\ \text{share a generator and prime} & & & \\ \text{modulus.} & & & \\ \text{Each then secretly picks a} & n = 8 & \text{secret number} & n=6 \\ \text{number n of their own.} & & & \\ \text{Each calculates } g^n \bmod p & 3^{8} \bmod 17=16 & & 3^{6} \bmod 17=15 \\ \text{They then exchange these} & A=16 & & B=15 \\ \text{resulting values.} & B=15 & & A=16\\ \text{Each then raises the value} & B^{n} \bmod p= & \text{mix in secret} & A^{n} \bmod p=\\ \text{they received to the power of } & & \text{number} & \\ \text{their secret }n \bmod p & 15^{8} \bmod 17=1 & & 16^{6} \bmod 17=1\\ \text{The result is the shared secret key.} & 1 & \text{shared secret key} & 1 \end{array}\)
Los secretos compartidos salen de la misma manera debido a la regla de potencia de exponente modular
\(\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{c} \bmod n\right)^{b} \bmod n .\)Alice\(\left(3^{6} \bmod 17\right)^{8} \bmod 17\) computó mientras Bob\(\left(3^{8} \bmod 17\right)^{6} \bmod 17,\) computó lo que dice
la regla dará los mismos resultados.
Observe que aunque un fisgón obtuviera ambos valores intercambiados\(A=16\) y\(B=15\), no hay forma de que puedan obtener la clave secreta compartida de estos sin tener al menos uno de los números secretos de Alice o Bob. No hay manera fácil de obtener los números secretos a partir de los valores compartidos, ya que la función era una función unidireccional.
Usando este enfoque, Alice y Bob ahora pueden usar la clave secreta compartida obtenida como la clave para un algoritmo de cifrado estándar como DES o AES.
Supongamos que está haciendo un intercambio de claves con Kylie usando generador 5 y prime 23. Tu número secreto es 2. ¿Qué número le mandas a Kylie? Si Kylie le envía el valor 8, determine la clave secreta compartida.
- Contestar
-
Para calcular el número que le enviaríamos a Kylie, elevamos el generador a la potencia de nuestro módulo numérico secreto el primo:\(5^{2} \bmod 23=25 \bmod 23=2\).
Si Kylie nos envía el valor\(8,\) determinamos el secreto compartido elevando su número a la potencia de nuestro módulo numérico secreto el primo:\(8^{2} \bmod 23=64 \bmod 23=18.18\) sería el secreto compartido.
RSA
Hay varios otros métodos de clave pública utilizados, incluyendo RSA, que se usa muy comúnmente. RSA implica distribuir una clave de cifrado pública, que cualquiera puede usar para encriptar mensajes para usted, pero que solo se puede descifrar usando una clave privada separada. Se puede pensar en esto como enviar un candado abierto a alguien — ellos pueden bloquear la información, pero nadie puede desbloquearla sin la llave que mantuviste en secreto.
La seguridad de RSA se basa en la dificultad de factorizar grandes números. Por ejemplo, es fácil calcular que 53 veces 59 es 3127, pero dado el número 12,317 que es producto de dos primos, es mucho más difícil encontrar los números que se multiplican para dar ese número. Es exponencialmente más difícil cuando cada uno de los primos tiene 100 o más dígitos. Supongamos que encontramos dos primos\(p\) y\(q\) y los multiplicamos para conseguir\(n=p q\). Este número será muy difícil de factorizar. Si también sabemos\(p\) y\(q\), hay atajos para encontrar dos números\(e\) y\(d\) así que\(m^{e d} \bmod n=m \bmod n\) para todos los números\(m\). Sin conocer la factorización de\(n\), encontrar estos valores es muy difícil.
Para usar RSA, generamos dos primos\(p\) y\(q\) y los multiplicamos para obtener\(n=p q\). ya que conocemos la factorización, podemos encontrar fácilmente\(e\) y\(d\) así\(m^{e d}=m \bmod n .\) Ahora,\(d .\) bloqueamos\(p\)
\(q,\) y luego enviamos los valores\(e\) y \(n\)hacia fuera publicamente. Para cifrar un mensaje que\(m,\) el remitente calcula\(S=m^{e} \bmod n .\) Como vimos anteriormente, el módulo es una función unidireccional que hace que el mensaje original sea muy difícil de recuperar\(S\). Sin embargo, tenemos nuestra clave privada\(d\) que podemos usar para descifrar el mensaje. Cuando recibimos el mensaje secreto\(S\), calculamos\(S^{d} \bmod n=\left(m^{e}\right)^{d} \bmod n=m^{e d} \bmod n=m \bmod n,\) recuperando el mensaje original [4].
Supongamos que Alice ha calculado\(n=3127, e=3,\) y\(d=2011 .\) Muestra cómo Bob cifraría el mensaje 50 y cómo Alice lo descifraría entonces.
Solución
Bob solo conocería su mensaje,\(m=50\) y la clave pública de Alice:\(n=3127\) y\(e=3 .\) cifraría el mensaje computando\(m^{e} \bmod n: 50^{3} \bmod 3127=3047\)
Alice puede entonces descifrar este mensaje usando su clave privada\(d\) computando\(S^{d}\) mod\(n\):
\(3047^{2011} \bmod 3127=50\)
Este método difiere de Diffie-Hellman-Merkle porque no se necesita ningún proceso de intercambio; Bob podría enviar a Alice un mensaje cifrado usando la clave pública de Bob sin tener que comunicarse con Alice de antemano para determinar una clave secreta compartida. Esto es especialmente útil para aplicaciones como el cifrado de correo electrónico, donde es posible que ambas partes no estén en línea al mismo tiempo para realizar un intercambio de claves estilo Diffie-Hellman-Merkle.
[1] es.wikipedia.org/w/index.php?... nge.svg&page=1
[2] Para una visión general en video de este proceso, consulte http://www.youtube.com/watch?v=YEBfamv-_do
[3] En algún momento, en lugar de ver 17 mod 5 = 2, verás 17 ≡ 2 (mod 5). El símbolo ≡ significa “congruente con” y significa que 17 y 2 son equivalentes, después de considerar el módulo 5.
[4] Se han dejado fuera muchos detalles, entre ellos cómo se determinan e y d, y por qué todo esto funciona. Para un poco más de detalle, consulte http://www.youtube.com/watch?v=wXB-V_Keiu8, o http://doctrina.org/How-RSA-Works-With-Examples.html