2.5: Ecuaciones Lineales - Manipulación y Resolución (Resolviendo el Rompecabezas)
- Page ID
- 110657
Estás comprando en Old Navy siete atuendos nuevos. Los puntos de precio son $10 y $30. Te gustan mucho los outfits de $30; sin embargo, tu presupuesto total no puede superar los 110 dólares. ¿Cómo gastas 110 dólares para adquirir todos los atuendos necesarios sin exceder tu presupuesto mientras consigues tantos artículos de $30 como sea posible?
Este es un problema de ecuaciones lineales, e ilustra cómo puedes usarlas para tomar una decisión óptima. Dejar\(L\) representar la cantidad de ropa en el punto de precio bajo de $10, y\(H\) representar la cantidad de ropa en el punto de precio alto de $30. Esto da como resultado las siguientes ecuaciones algebraicas:
\[L+H=7 \text { (the total number of outfits you need) }\nonumber \]
\[\$ 10 L+\$ 30 H=\$ 110 \text { (your total budget) }\nonumber \]
Al resolver simultáneamente estas ecuaciones puedes determinar cuántos atuendos en cada punto de precio puedes adquirir.
Te encontrarás con muchas situaciones como esta en tu carrera empresarial, por ejemplo, en hacer el mejor uso de la capacidad de producción de un fabricante. Supongamos que su empresa fabrica dos productos en la misma línea de producción y vende toda su producción. Cada producto contribuye de manera diferente a su rentabilidad, y cada producto tarda una cantidad diferente de tiempo en fabricarse. ¿Qué combinación de cada uno de estos productos debe hacer de tal manera que opere su línea de producción a su capacidad al tiempo que maximiza las ganancias obtenidas? Esta sección explora cómo resolver ecuaciones lineales para variables desconocidas.
Comprensión de ecuaciones
Para manipular ecuaciones algebraicas y resolver variables desconocidas, primero debe familiarizarse con algún lenguaje importante, incluyendo ecuaciones lineales versus no lineales y lados de la ecuación.

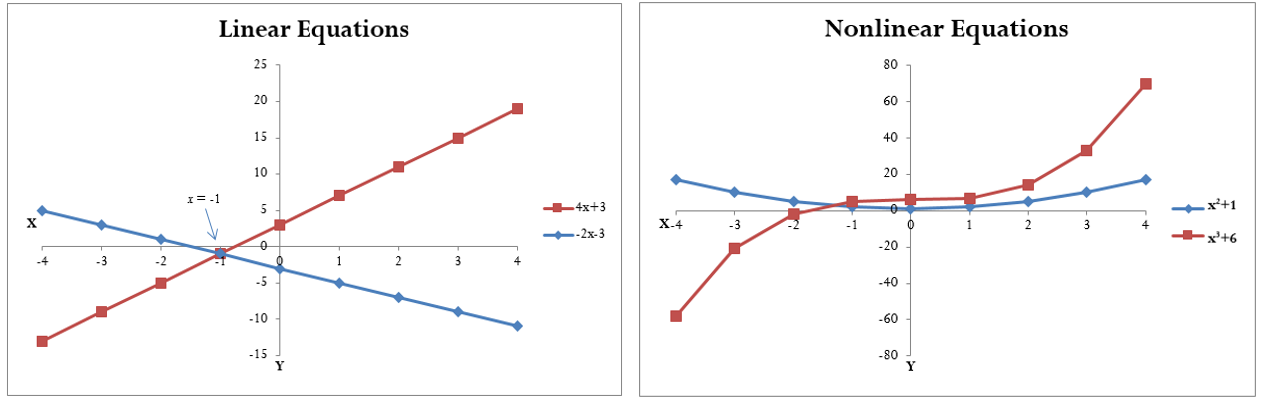
El objetivo al manipular y resolver una ecuación lineal es encontrar un valor para la variable desconocida que haga verdadera la ecuación. Si sustituye un valor de\(x = −1\) en el ejemplo anterior, el lado izquierdo de la ecuación es igual al lado derecho de la ecuación (ver Figura a continuación). El valor de\(x = −1\) se conoce como la raíz, o solución, a la ecuación lineal.
Resolviendo una ecuación lineal con una variable desconocida
En su estudio de resolución de ecuaciones lineales, debe comenzar manipulando una sola ecuación para resolver para una sola variable desconocida. Posteriormente en esta sección se extenderá desde esta fundación hasta la solución de dos ecuaciones lineales con dos incógnitas.
Cómo funciona
Para determinar la raíz de una ecuación lineal con una sola variable desconocida, aplique los siguientes pasos:
Paso 1: Tu primer objetivo es separar los términos que contienen el coeficiente literal de los términos que solo tienen coeficientes numéricos. Recoja todos los términos con coeficientes literales en un solo lado de la ecuación y recoja todos los términos con solo coeficientes numéricos en el otro lado de la ecuación. No importa qué términos vayan de qué lado de la ecuación, siempre y cuando los separes.
Para mover un término de un lado de una ecuación a otro, tomar el opuesto matemático del término que se mueve y agregarlo a ambos lados. Por ejemplo, si quieres mover el +3 in\(4x + 3 = −2x − 3\) del lado izquierdo al lado derecho, el opuesto matemático de +3 es −3. Cuando mueves un término, recuerda la regla cardinal: Lo que haces a un lado de una ecuación también debes hacer al otro lado de la ecuación. Romper esta regla rompe la igualdad en la ecuación.
Paso 2: Combina todos los términos similares en cada lado y simplifica la ecuación de acuerdo a las reglas del álgebra.
Paso 3: En el término que contiene el coeficiente literal, reducir el coeficiente numérico a un 1 dividiendo ambos lados de la ecuación por el coeficiente numérico.
Notas Importantes
Cuando no está seguro de si su raíz calculada es precisa, una manera fácil de verificar su respuesta es tomar la ecuación original y sustituir su raíz en lugar de la variable. Si tienes la raíz correcta, el lado izquierdo de la ecuación es igual al lado derecho de la ecuación. Si tienes una raíz incorrecta, los dos lados serán desiguales. La desigualdad suele ser el resultado de uno de los tres errores más comunes en la manipulación algebraica:
- Se han roto las reglas de BEDMAS.
- Se han violado las reglas del álgebra.
- Lo que se hizo a un lado de la ecuación no se hizo al otro lado de la ecuación.
Cosas a tener en cuenta
Cuando mueves un término de un lado de la ecuación a otro usando multiplicación o división, recuerda que esto afecta a todos y cada uno de los términos en ambos lados de la ecuación. Para eliminar el\(x\) del denominador en la siguiente ecuación, multiplique ambos lados de la ecuación por\(x\):
\(\dfrac{5}{x}+\dfrac{1}{x}=\dfrac{2}{x}+2\)se convierte en\(x\left(\dfrac{5}{x}+\dfrac{1}{x}\right)=\left(\dfrac{2}{x}+2\right) x\) que luego se convierte\(5+1=2+2 x\)
Multiplicar cada término de ambos lados por\(x\) mantiene la igualdad.
Caminos hacia el éxito
Los números negativos pueden causar mucho dolor a algunas personas. Al mover términos desde un lado particular de la ecuación, muchas personas prefieren evitar los coeficientes numéricos negativos frente a los coeficientes literales. Revisando\(4x + 3 = −2x − 3\), podrías mover el\(4x\) del lado izquierdo al lado derecho restando\(4x\) de ambos lados. Sin embargo, en el lado derecho esto resulta en\(−6x\). El negativo se pasa por alto fácilmente o se cae accidentalmente en pasos futuros. En su lugar, mueva la variable hacia el lado izquierdo de la ecuación, produciendo un coeficiente positivo de\(6x\).
Tomemos el ejemplo en curso en esta sección y resolverlo para\(x\):\(4x + 3 = −2x − 3\)
Solución
Esta es una ecuación lineal ya que el exponente sobre la variable es 1. Estás para resolver la ecuación y encontrar la raíz para\(x\).
Lo que ya sabes
Ya se ha proporcionado la ecuación.
Cómo Llegarás Allí
Aplicar los tres pasos para resolver ecuaciones lineales. Para llegar a la raíz, debes seguir las reglas del álgebra, BEDMAS, e igualdad.
Realizar
Paso 1: Mover términos con coeficientes literales a un lado y términos con solo coeficientes numéricos al otro lado. Recopilemos el coeficiente literal en el lado izquierdo de la ecuación. Muévete\(−2x\) hacia el lado izquierdo colocándolo\(+2x\) en ambos lados.
\[4x + 3 = −2x – 3 \nonumber \]
En el lado derecho, el\(−2x\) y\(+2x\) cancelar a cero.
\[4x + 3 (\bf{+ 2x}) = −2x − 3 (\bf{+ 2x}) \nonumber \]
Paso 1 (continuación): Todos los términos con el coeficiente literal están ahora a la izquierda. Movamos todos los términos que contienen solo coeficientes numéricos hacia el lado derecho. Mueva el +3 hacia el lado derecho colocando −3 en ambos lados.
\[4x + 3 + 2x = −3 \nonumber \]
En el lado izquierdo, los +3 y −3 cancelan a cero.
\[4x + 3 + 2x (\bf{– 3}) = −3 (\bf{− 3}) \nonumber \]
Paso 2: Ahora los términos están separados. Combina términos similares de acuerdo a las reglas del álgebra.
\[4x + 2x = −3 – 3 \nonumber \]
Paso 3: El término con el coeficiente literal se está multiplicando por el coeficiente numérico de 6. Por lo tanto, dividir ambos lados por 6.
\[\bf{6x = −6} \nonumber \]
Los coeficientes numéricos del lado izquierdo se dividirán a 1. Resuelve los coeficientes numéricos en el lado derecho.
\[\dfrac{6 x}{\bf{6}}=\dfrac{-6}{\bf{6}} \nonumber \]
Esta es la raíz de la ecuación.
\[x = −1 \nonumber \]
La raíz de la ecuación es\(x = −1\). Para verificar la exactitud de su manipulación, tome la raíz\(x = −1\) y sumétela en la ecuación original:
\[4(−1) + 3 = −2(−1) − 3\nonumber \]
\[−4 + 3 = 2 − 3\nonumber \]
\[−1 = −1\nonumber \]
El lado izquierdo es igual al lado derecho, por lo que la raíz es correcta.
Resuelve la siguiente ecuación para\(m\):\(\dfrac{3 m}{4}+2 m=4 m-15\)
Solución
Esta es una ecuación lineal ya que el exponente sobre la variable es un 1. Estás para resolver la ecuación y encontrar la raíz para\(m\).
Lo que ya sabes
Ya se ha proporcionado la ecuación.
Cómo Llegarás Allí
Simplifique primero las ecuaciones y luego aplique los tres pasos para resolver ecuaciones lineales. Para llegar a la raíz se deben seguir las reglas de álgebra, BEDMAS, e igualdad. Se puede utilizar un enfoque que evite los negativos.
Realizar
Primero, simplifique todas las fracciones para facilitar el trabajo con la ecuación.
\[\dfrac{3 m}{4}+2 m=4 m-15 \nonumber \]
Aún simplificando, recoja términos similares cuando sea posible.
\[(\bf{0.75m}) + 2m = 4m − 15 \nonumber \]
Paso 1: Recoge todos los términos con el coeficiente literal en un lado de la ecuación. Mueve todos los términos con coeficientes literales al lado derecho.
\[(\bf{2.75m })= 4m − 15 \nonumber \]
Paso 1 (continuación): Combina términos similares y mueve todos los términos con solo coeficientes numéricos hacia el lado izquierdo.
\[2.75m (\bf{− 2.75m}) = 4m − 15 (\bf{− 2.75m}) \nonumber \]
En el lado izquierdo, el\(+2.75m\) y se\(−2.75m\) cancelan entre sí. Ahora mueve los coeficientes numéricos hacia el lado izquierdo.
\[(\bf{0}) = 4m − 15 (\bf{− 2.75m}) \nonumber \]
En el lado derecho, los −15 y +15 se cancelan entre sí.
\[0 (\bf{+ 15 })= 4m − 15 − 2.75m (\bf{+ 15}) \nonumber \]
Paso 2: Combina términos similares en cada lado.
\[0 (\bf{+ 15}) = 4m − 2.75m \nonumber \]
Paso 3: Dividir ambos lados por el coeficiente numérico que acompaña al coeficiente literal.
\[\bf{15 = 1.25m} \nonumber \]
Simplificar.
\[\dfrac{15}{\bf{1.25}}=\dfrac{1.25 m}{\bf{1.25}} \nonumber \]
Esta es la raíz de la ecuación.
\[12=m\nonumber \]
La raíz de la ecuación es\(m = 12\).
Esto hace que ambos lados de la ecuación,
\(\dfrac{3 m}{4}+2 m\)y\(4 m-15\), igual 33.
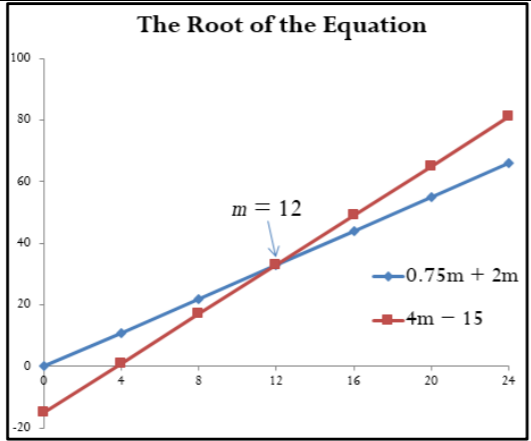
Resuelve la siguiente ecuación\(b\) y redondea tu respuesta a cuatro decimales:\(\dfrac{5}{8} b+\dfrac{2}{5}=\dfrac{17}{20}-\dfrac{b}{4}\)
Solución
Esta es una ecuación lineal ya que el exponente sobre la variable es un 1. Estás para resolver la ecuación y encontrar la raíz para\(b\).
Lo que ya sabes
Ya se ha proporcionado la ecuación. Aunque podrías intentar borrar todas y cada una de las fracciones o intentar encontrar un denominador común, recuerda que puedes eliminar fracciones convirtiéndolas en decimales.
Cómo Llegarás Allí
Simplifica las fracciones en forma decimal. Luego aplique los tres pasos para resolver ecuaciones lineales. Para llegar a la raíz, debes seguir las reglas del álgebra, BEDMAS, e igualdad.
Realizar
Simplifica las fracciones y convierte a decimales.
\[\dfrac{5}{8} b+\dfrac{2}{5}=\dfrac{17}{20}-\dfrac{b}{4} \nonumber \]
Paso 1: Mueve los términos del coeficiente literal hacia el lado izquierdo.
\[(\bf{0.625})b (\bf{+ 0.4}) = (\bf{0.85 − 0.25})b \nonumber \]
Los coeficientes literales del lado derecho se cancelan entre sí.
\[0.625b + 0.4 + (\bf{0.25b}) = 0.85 − 0.25b + (\bf{0.25b}) \nonumber \]
Mueva los términos del coeficiente numérico hacia el lado derecho.
\[0.625b + 0.4 + 0.25b = 0.85 \nonumber \]
Los coeficientes numéricos del lado izquierdo se cancelan entre sí.
\[0.625b + 0.4 +0.25b (\bf{− 0.4}) = 0.85 (\bf{− 0.4}) \nonumber \]
Paso 2: Combina términos similares en cada lado.
\[0.625b + 0.25b = 0.85 − 0.4\nonumber \]
Paso 3: Dividir ambos lados por el coeficiente numérico que acompaña al coeficiente literal.
\[\bf{0.875b = 0.45} \nonumber \]
Simplificar.
\[\dfrac{0.875 b}{\bf{0.875}}=\dfrac{0.45}{\bf{0.875}} \nonumber \]
Redondear a cuatro decimales según las instrucciones.
\[b = 0.514285 \nonumber \]
Esta es la raíz.
\[b = 0.5143 \nonumber \]
La raíz de la ecuación, redondeada a cuatro decimales, es\(b = 0.5143\).
Resolver dos ecuaciones lineales con dos variables desconocidas
El proceso de manipulación que acabas de practicar funciona bien para resolver una ecuación lineal con una variable. Pero, ¿qué pasa si necesitas resolver dos ecuaciones lineales con dos variables simultáneamente? ¿Recuerdas cuando estabas en Old Navy comprando siete atuendos antes en este capítulo (ecuación 1)? Necesitabas estar dentro de un presupuesto de precios (ecuación 2). Cada ecuación tenía dos variables desconocidas que representaban el número de atuendos de menor precio y de mayor precio.
El objetivo es reducir dos ecuaciones con dos incógnitas en una sola ecuación lineal con una desconocida. Una vez completada esta transformación, entonces identifica la variable desconocida aplicando el procedimiento de tres pasos para resolver una ecuación lineal, como se acaba de discutir.
Cuando se trabaja con dos ecuaciones lineales con dos incógnitas, las reglas de álgebra permiten las siguientes dos manipulaciones:
- Lo que le hagas a un lado de la ecuación debe hacerse al otro lado de la ecuación para mantener la igualdad. Por lo tanto, se puede multiplicar o dividir cualquier ecuación por cualquier número sin cambiar la raíz de la ecuación. Por ejemplo, si multiplicas todos los términos de\(x + y = 2\) por 2 en ambos lados, resultando en\(2x + 2y = 4\), la igualdad de la ecuación permanece sin cambios y existen las mismas raíces.
- Los términos que están en el mismo lado de una ecuación se pueden sumar y restar entre ecuaciones combinando términos similares. Cada una de las dos ecuaciones tiene un lado izquierdo y un lado derecho. Esta regla permite tomar el lado izquierdo de la primera ecuación y o bien sumar o restar términos similares en el lado izquierdo de la segunda ecuación. Cuando realices esta acción, recuerda la primera regla anterior. Si suma los lados izquierdos de las ecuaciones juntos, entonces debe sumar el lado derecho de ambas ecuaciones para mantener la igualdad.
Cómo funciona
Sigue estos pasos para resolver dos ecuaciones lineales con dos variables desconocidas:
Paso 1: Escribe las dos ecuaciones una encima de la otra, alineando verticalmente términos que tengan los mismos coeficientes literales y términos que tengan únicamente el coeficiente numérico. Si es necesario, las ecuaciones pueden necesitar ser manipuladas de tal manera que todos los coeficientes literales estén en un lado con los coeficientes numéricos en el otro lado.
Paso 2: Examina tus dos ecuaciones. A través de la multiplicación o división, hacer el coeficiente numérico en uno de los términos que contienen un coeficiente literal exactamente igual a su contraparte en la otra ecuación.
Paso 3: Suma o resta las dos ecuaciones según sea necesario para eliminar el término idéntico de ambas ecuaciones.
Paso 4: En la nueva ecuación, resolver para el último coeficiente literal.
Paso 5: Sustituir la raíz del coeficiente literal conocido en cualquiera de las dos ecuaciones originales. Si una de las ecuaciones adquiere una estructura más simple, elija esa ecuación.
Paso 6: Resuelve tu ecuación elegida para el otro coeficiente literal.
Caminos hacia el éxito
A veces no está claro exactamente cómo se necesita multiplicar o dividir las ecuaciones para hacer dos de los términos idénticos. Por ejemplo, supongamos las siguientes dos ecuaciones:
\[4.9x + 1.5y = 38.3\nonumber \]
\[2.7x − 8.6y = 17.8\nonumber \]
Si el objetivo es hacer\(x\) idénticos los términos que contienen el coeficiente literal, existen dos soluciones alternativas:
- Tome el coeficiente numérico más grande para\(x\) y divídalo por el coeficiente numérico más pequeño. El número resultante es el factor para multiplicar la ecuación que contiene el coeficiente numérico más pequeño. En este caso,\(4.9 \div 2.7 =1 . \overline{814}\). Multiplique todos los términos de la segunda ecuación por\(1 . \overline{814}\) para hacer que los coeficientes numéricos sean\(x\) iguales entre sí, dando como resultado este par de ecuaciones:
\[4.9x + 1.5y = 38.3\nonumber \]
\[4.9 x-15.6 \overline{074} y=32.3 \overline{037} \text { (every term multiplied by } 1 . \overline{814})\nonumber \]
- Toma la primera ecuación y multiplícala por el coeficiente numérico en la segunda ecuación. Después toma la segunda ecuación y multiplícala por el coeficiente numérico en la primera ecuación. En este caso, multiplique todos los términos de la primera ecuación por 2.7. Después multiplica todos los términos de la segunda ecuación por 4.9.
\[13.23 x+4.05 y=103.41 \text { (every term multiplied by } 2.7)\nonumber \]
\[13.23 x-42.14 y=87.22 \text { (every term multiplied by 4.9) }\nonumber \]
Tenga en cuenta que ambos enfoques dan como resultado con éxito que ambas ecuaciones tengan el mismo coeficiente numérico frente al coeficiente literal\(x\).
Caminos hacia el éxito
En última instancia, cada emparejamiento de ecuaciones lineales con dos incógnitas se puede convertir en una sola ecuación a través de la sustitución. Para realizar la conversión, haga lo siguiente:
- Resolver cualquiera de las ecuaciones para una de las variables desconocidas.
- Tomar la expresión algebraica resultante y sustituirla en la otra ecuación. Esta nueva ecuación es solucionable para una de las variables desconocidas.
- Sustituya su nueva variable por una de las ecuaciones originales para determinar el valor de la otra variable desconocida.
Tome las siguientes dos ecuaciones:
\[a + b = 4 \quad \quad 2a + b = 6\nonumber \]
- Resolviendo la primera ecuación para un resultado en\(a = 4 - b\).
- Sustituir la expresión por a en la segunda ecuación y resolver por b da como resultado\(2(4 - b) + b = 6\), que resuelve como\(b = 2\).
- Finalmente, sustituyendo la raíz de b en la primera ecuación para calcular a da\(a + 2 = 4\) como resultado\(a = 2\). Por lo tanto, las raíces de estas dos ecuaciones son\(a = 2\) y\(b = 2\).
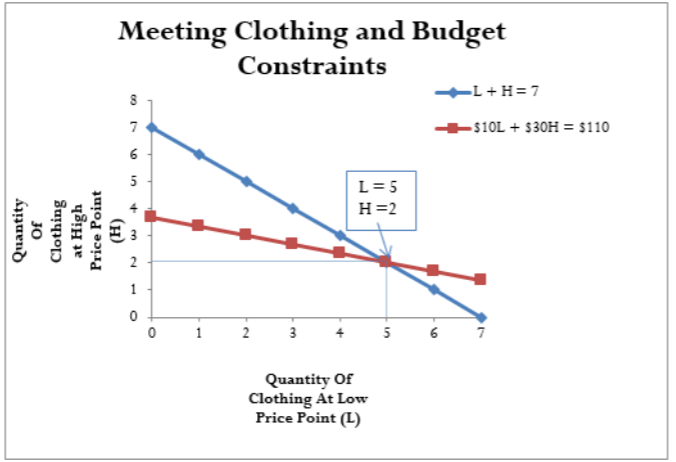
Recordemos del abridor de sección que en la compra de atuendos hay dos puntos de precio de $10 y $30, tu presupuesto es de 110 dólares, y que necesitas siete prendas de vestir. Las siguientes ecuaciones representan estas condiciones. Identifica cuántos atuendos de bajo precio (\(L\)) y atuendos de alto precio (\(H\)) puedes comprar.
\[L + H = 7 \text{ } \$10L + \$30H = $110\nonumber \]
Solución
Debe determinar la cantidad de artículos de bajo precio\(L\), o artículos de alto precio\(H\), o que están dentro de su presupuesto limitado. Obsérvese que los exponentes sobre las variables son 1 y que hay dos incógnitas. Entonces hay dos ecuaciones lineales con dos incógnitas.
Lo que ya sabes
Se requieren siete prendas de vestir y sólo se tiene un presupuesto de 110 dólares. Las ecuaciones expresan las relaciones de cantidad y presupuesto.
Cómo Llegarás Allí
Aplicar el procedimiento de seis pasos para resolver dos ecuaciones lineales con dos incógnitas.
Paso 1:
Escribe las ecuaciones una encima de la otra y alinéalas.
\[\begin{array} {lllll} {L} & + &{H}& = &{7}\\ {\$10L} & + &{\$30H}& = &{\$110}\\ \end{array} \nonumber \]
Paso 2:
Multiplique todos los términos de la primera ecuación por 10 para que\(L\) tenga el mismo coeficiente numérico en ambas ecuaciones.
\[\begin{array} {lllll} {10L} & + &{10H}& = &{70}\\ {\$10L} & + &{\$30H}& = &{\$110}\\ \end{array} \nonumber \]
Paso 3:
Restar las ecuaciones restando todos los términos en ambos lados.
\[\begin{array} {llllll} { } &{10L} & + &{10H}& = &{70}\\ {\text{subtract}} &{\$10L} & + &{\$30H}& = &{\$110}\\{ } &{ } & - &{\$20H}& = &{−\$40}\\ \end{array} \nonumber \]
Paso 4:
Resuelve\(H\) dividiendo ambos lados por −20.
\[\dfrac{-\$ 20 H}{-\$ 20}=\dfrac{-\$ 40}{-\$ 20} \quad H=2 \nonumber \]
Paso 5:
Sustituir el valor conocido por\(H\) en una de las ecuaciones originales. La primera ecuación es simple, así que elige esa.
\[\begin{array} {lllll} {L} & + &{H}& = &{7}\\ {L} & + &{2}& = &{7}\\ \end{array} \nonumber \]
Paso 6:
Resuelve\(L\) restando 2 de ambos lados. Ahora tienes las raíces para\(L\) y\(H\).
\[\begin{array} {lllllllll} {L}&+&{2} & - &{2}& = &{7}&-&{2}\\ { } & { } &{ } & { } &{L}& = &{5} & { } & { }\\ \end{array} \nonumber \]
Se pueden adquirir cinco prendas de vestir en el punto de precio bajo y dos prendas de vestir al punto de precio alto. Esto le permite adquirir siete prendas de vestir y mantenerse dentro de su presupuesto de $110.
Caminos hacia el éxito
Una de las áreas más difíciles de las matemáticas consiste en traducir palabras en símbolos y operaciones matemáticas. Para ayudar en esta traducción, la siguiente tabla enumera algún lenguaje común y el símbolo matemático que normalmente se asocia con la palabra o frase.
| Lenguaje | Símbolo matemático | ||
|---|---|---|---|
|
Suma Adición |
Además de En exceso |
Incrementado por Plus |
+ |
|
Restar Disminuido por Disminuido por |
Menos Menos |
Diferencia Reducida por |
- |
|
multiplicado por Veces |
Porcentaje de |
Producto de De |
× |
|
Dividir División |
Divisible Cociente |
Per | ÷ |
|
Se convierte ES/Fuas/Eran |
Serán |
Resultados en Totales |
= |
| Más de | Mayor que | > | |
| Menos de | Inferior a | < | |
| Mayor o igual a | ≥ | ||
| Menor o igual a | ≤ | ||
| No es igual a | ≠ | ||
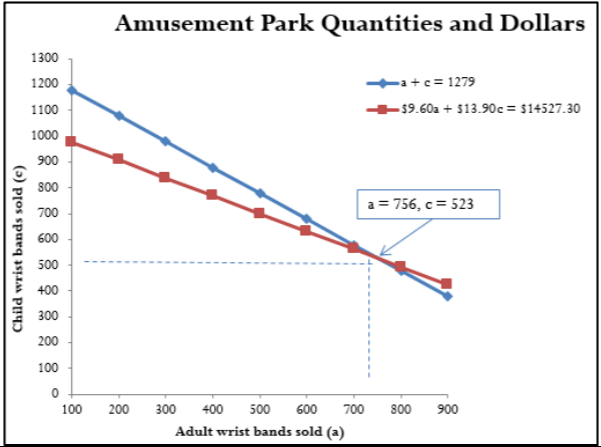
Tinkertown Family Fun Park cobra $15 por una muñequera infantil y $10.50 por una muñequera para adultos. En un cálido día de verano, el parque de diversiones tuvo ingresos totales de 15 mil 783 dólares por ventas de 1,279 muñequeras. ¿Cuántas muñequeras para adultos y niños vendió el parque ese día?
Solución
Necesitas el número de muñequeras tanto para adultos como para niños vendidas en el día dado. Por lo tanto, se deben identificar dos incógnitas.
Lo que ya sabes
Se conocen el precio de las muñequeras, la cantidad total y las ventas:
Precio de muñequera infantil = $15
Precio de la muñequera para adultos = $10.50
Ingresos totales = $15,783
Ventas totales por unidad = 1,279
Se desconocen la cantidad de muñequeras para adultos vendidas y la cantidad de muñequeras infantiles vendidas:
Cantidad de muñequeras para adultos =\(a\)
Cantidad de muñequeras infantiles =\(c\)
Cómo Llegarás Allí
- Trabajar primero con las cantidades. Calcule las ventas totales de unidades sumando el número de muñequeras para adultos al número de muñequeras infantiles:
\[\# \text { of adult wrist bands }+\# \text { of child wrist bands }=\text { total unit sales } \nonumber \]
\[a + c = 1,279\nonumber \]
- Ahora considere las cifras del dólar. Los ingresos totales para cualquier compañía se calculan como precio unitario multiplicado por unidades vendidas. En este caso, debes sumar los ingresos de dos productos para obtener los ingresos totales.
\[\text { Total adult revenue }+\text { Total child revenue }=\text { Total revenue }\nonumber \]
\[\text { (Adult price } \times \text { Adult guantity })+\text { (Child price } \times \text { Child quantity) }=\text { Total revenue }\nonumber \]
\[\$ 10.50 a+\$ 15 c=\$ 15,783\nonumber \]
- Aplicar el procedimiento de seis pasos para resolver dos ecuaciones lineales con dos incógnitas.
Realizar
Paso 1:
Escribe las ecuaciones una encima de la otra y alinéalas.
\[\begin{array} {lllll} {a} & + &{c}& = &{1,279}\\ {\$10.50a} & + &{\$15c}& = &{\$15,783}\\ \end{array} \nonumber \]
Paso 2:
Multiplique todos los términos de la primera ecuación por 10.5, resultando en tener el mismo coeficiente numérico en ambas ecuaciones.
\[\begin{array} {lllll} {\bf{10.50} a} & + &{\bf{10.50} c} & = & {\bf{13,429.50}} \\ {\$10.50a} & + &{\$15c}& = &{\$15,783}\\ \end{array} \nonumber \]
Paso 3:
Restar las ecuaciones restando todos los términos en ambos lados.
\[\begin{array} {llllll} { } & {\bf{10.50} a} & + &{\bf{10.50} c} & = & {\bf{13,429.50}} \\ {\text{Subtract}} & {\underline{\$10.50a}} & {\underline{+}} &{\underline{\$15c}} & {\underline{=}} &{\underline{\$15,783}}\\ { } & { } & { } & {\bf{-4.5c}} & {\bf{=}} & {\bf{-2,353.50}} \\ \end{array} \nonumber \]
Paso 4:
Resuelve\(c\) dividiendo ambos lados por −4.5.
\[\dfrac{-4.5 c}{-4.5}=\dfrac{-2,353.50}{-4.5} \quad c=523 \nonumber \]
Paso 5:
Sustituir el valor conocido por\(c\) en una de las ecuaciones originales. La primera ecuación es simple, así que elige esa.
\[\begin{array} {lllll} {a} & + & {c} & = &{1,279} \\ {a} & + & {\bf{523}} & = &{1,279}\\ \end{array} \nonumber \]
Paso 6:
Resuelve para una restando 523 de ambos lados. Ahora tienes las raíces para\(a\) y\(c\).
\[\begin{aligned} a+523 \bf{-523} &=1,279 \bf{-523} \\ a &=756 \end{aligned} \nonumber \]
Tinkertown Family Fun Park vendió 523 muñequeras infantiles y 756 muñequeras para adultos.