9.4: Pagos equivalentes
- Page ID
- 110861
Los imprevistos y las circunstancias pueden obligarte a reorganizar tus compromisos financieros. Cuando esto sucede, el nuevo acuerdo tiene que ser justo para todas las partes interesadas.
Supongamos que usted y sus compañeros de trabajo confían en los bonos navideños anuales de su empresa. No obstante, el director general acaba de anunciar que debido a las duras condiciones económicas nadie va a obtener un bono este año. Ya destinaste ese dinero para pagar una deuda de 5.000 dólares que vence la próxima semana. Quieres ser financieramente responsable, pero no es posible que hagas el pago. Antes de levantar el teléfono para llamar a tu acreedor, debes determinar qué curso de acción debes seguir.
Es necesario hacer arreglos alternativos que dejen a su acreedor en la misma situación financiera que lo hizo el acuerdo original. Usted vio en la sección anterior que si iba a realizar un pago anticipado, el pago debería ser reducido por una tasa de descuento acordada. En este caso, sin embargo, vas a hacer un pago atrasado, por lo que debes otorgar intereses al acreedor. Así, si propones pagar la deuda con seis meses de retraso y tu acreedor acepta 9% compuesto mensual como tasa justa, entonces debes $5,229.26 (aplicando la Fórmula 9.3).
Este concepto se aplica a todos los aspectos de tu vida personal y profesional. A excepción de los regalos, las deudas personales con amigos o familiares deben tener algún interés. Todos deben ser financieramente justos el uno con el otro. Un negocio debe estar dispuesto a trabajar con sus clientes en el caso de que necesite alterar un acuerdo. Una empresa que es inflexible tiende a encontrarse amortizando deudas incobrables o persiguiendo acciones legales desagradables y a veces costosas.
Esta sección explora el concepto de flujos de pago equivalentes. Esto implica equiparar dos o más corrientes financieras alternativas para garantizar que ninguna de las partes sea penalizada por elección alguna. A continuación, se aplica el concepto de valor presente a los préstamos y pagos de préstamos.
Conceptos Fundamentales
El concepto fundamental del valor del dinero en el tiempo
Todos los números en una ecuación deben expresarse en las mismas unidades, como kilómetros o metros. En el caso del dinero, tratas el momento en el que estás considerando el valor como la “unidad” que necesita ser la misma. Por intereses, un dólar hoy no es lo mismo que un dólar hace un año o un dólar dentro de un año, por lo que no se pueden mezclar dólares de diferentes épocas dentro de una misma ecuación; hay que llevar todos los dineros hacia adelante o hacia atrás a un punto común en el tiempo, llamado fecha focal.
El concepto fundamental de valor temporal del dinero establece que todo el dinero debe llevarse a la misma fecha focal antes de que se puedan determinar las operaciones matemáticas, decisiones o equivalencias, incluyendo las siguientes:
- Matemáticas simples como suma o resta.
- Decidir si adoptar acuerdos financieros alternativos.
- Determinar si las corrientes de pago son iguales.
El concepto fundamental de equivalencia
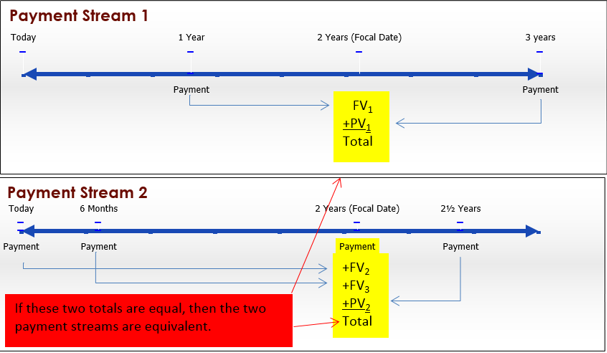
El concepto fundamental de equivalencia establece que dos o más flujos de pago son iguales entre sí si tienen el mismo valor económico en la misma fecha focal. Como se ilustra en la figura, las dos corrientes financieras alternativas son equivalentes si el total de Payment Stream 1 es igual al total de Payment Stream 2 en la misma fecha focal. Tenga en cuenta que el dinero involucrado en cada flujo de pago se puede sumar en la fecha focal debido al concepto fundamental de valor temporal del dinero.
Pagos equivalentes
Usted realiza flujos de pago alternativos equivalentes entre sí aplicando una tasa de interés prevaleciente que permita lo siguiente:
- Cualquier pago atrasado a cobrar intereses a través de cálculos de valor futuro (Sección 9.2)
- Cualquier pago anticipado para tener intereses deducidos a través de cálculos de valor presente (Sección 9.3)
La Fórmula
La buena noticia es que no necesitas nuevas fórmulas. Dependiendo de la estructura de las corrientes de pago que deban equipararse, aplique la Fórmula 9.3 tal cual o reorganice la fórmula para\(PV\). Como se ilustra en la figura anterior, la Corriente de Pago 1 implica calcular un valor futuro y un valor presente para trasladar el dinero a la fecha focal. El flujo de pago 2 implica calcular dos valores futuros y un valor presente. Una vez que todo el dinero se mueve a la misma fecha focal, se trabaja con la igualdad entre los valores de las dos corrientes de pago, resolviendo cualquier variable o variables desconocidas.
Cómo funciona
Siga estos pasos para resolver una pregunta de pago equivalente:
Paso 1: Dibujar tantos plazos como sea necesario para ilustrar cada uno de los acuerdos originales y propuestos. Indique claramente fechas, montos de pago y la (s) tasa (s) de interés.
Paso 2: Elige una fecha focal a la que se moverá todo el dinero.
Paso 3: Calcular todas las tasas de interés periódicas necesarias usando la Fórmula 9.1.
Paso 4: Calcula N para cada pago usando la Fórmula 9.2.
Paso 5: Realizar el cálculo del valor de tiempo apropiado usando la Fórmula 9.3.
Paso 6: Equiparar los valores de los acuerdos originales y propuestos en la fecha focal y resolver para cualquier incógnitas.
Supongamos que hoy debes $1,000 y $1,000 dentro de un año. Te encuentras incapaz de realizar ese pago hoy, por lo que indicas a tu acreedor que quieres realizar ambos pagos dentro de seis meses en su lugar. Las tasas de interés prevalecientes están en 6% compuestas semestralmente. ¿Qué pago único dentro de seis meses (el flujo de pago propuesto) equivale a los dos pagos (el flujo de pago original)?
Paso 1: La línea de tiempo ilustra el escenario.
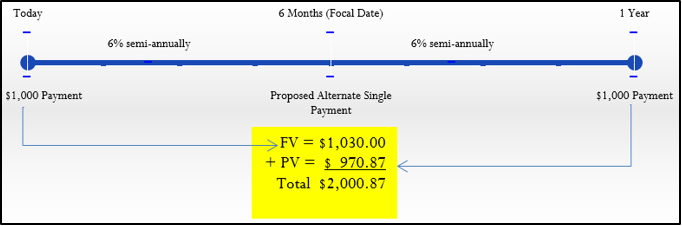
Paso 2: Aplicar el concepto fundamental de valor temporal del dinero, moviendo todo el dinero a la misma fecha. Dado que el pago propuesto es por seis meses a partir de ahora, eliges una fecha focal de seis meses.
Paso 3: Obsérvese que la composición semestral significa\(CY\) = 2. A partir de la Fórmula 9.1,\(I=6 \% / 2=3 \%\).
Paso 4: La Fórmula 9.2 produce\(N=2 \times \dfrac{1}{2}=1\) compuesto para ambos pagos (cada uno se mueve\(\dfrac{1}{2}\) al año).
Paso 5: Trasladando el pago de hoy de $1,000 seis meses hacia el futuro, tienes\(FV=\$ 1,000(1+0.03)^{1}=\$ 1,030.00\). Trasladando el pago futuro de $1,000 seis meses antes, tienes\(\$ 1,000=PV(1+0.03)^{1} \text { or } PV=\$ 970.87\).
Paso 6: Ahora que el dinero se ha movido a la misma fecha se pueden sumar los dos totales para determinar el pago equivalente, que es\(\$ 1,030.00+\$ 970.87=\$ 2,000.87\). Tenga en cuenta que esto es financieramente justo para ambas partes. Por realizar tu pago de $1,000 con seis meses de retraso, el acreedor te está cobrando $30 de interés. Además, por realizar tu segundo pago de $1,000 seis meses antes, estás recibiendo un beneficio de $29.13. Esto deja a ambas partes compensadas equitativamente: Ninguna de las partes está financieramente mejor o peor por el cambio en el trato.
Caminos hacia el éxito
Cuando haces dos (o más) flujos de pago iguales entre sí, dos propinas facilitarán el procedimiento:
- Líneas de tiempo adecuadas Las líneas de tiempo te ayudan a ver qué hacer. Si dibujas dos o más líneas de tiempo, alinéalas verticalmente, asegurando que todas las fechas correspondientes estén en las mismas columnas. Esto permite ver qué pagos deben valorarse en el futuro y cuáles deben estar presentes valorados para expresarlos en términos de la fecha focal elegida.
- Localiza la Fecha Focal en un Desconocido En un sentido, no importa qué fecha focal elijas porque dos valores que son iguales cuando se mueven a una fecha en común seguirán siendo iguales cuando ambos se muevan juntos a otra fecha. Pero debes simplificar tus cálculos seleccionando una fecha focal correspondiente a la fecha de una variable desconocida. Entonces cuando calcules la raíz de la ecuación, ya estará en la cantidad correcta en la fecha correcta. No se requerirán más cálculos para mover el dinero a su fecha correcta. Por ejemplo, en el escenario anterior había que determinar el monto de un pago que debía hacerse dentro de seis meses. Al establecer la fecha focal en seis meses, la fecha de lo desconocido que estabas tratando de encontrar, evitaste cualquier conversión adicional.
Johnson's Garden Centre no ha sido rentable recientemente y concluye que no puede hacer dos pagos de deuda por $4,500 con vencimiento hoy y otros $6,300 con vencimiento en tres meses. Después de discusiones entre Johnson's Garden Center y su acreedor, las dos partes coinciden en que ambos pagos podrían realizarse dentro de nueve meses, con intereses en 8.5% compuestos mensualmente. ¿Qué pago total necesita Johnson's Garden Centre dentro de nueve meses para liquidar su deuda?
Solución
Calcular y sumar el valor futuro de cada uno de los pagos atrasados en el punto de nueve meses con intereses, o\(FV\) para ambos.
Lo que ya sabes
Paso 1:
El monto de los pagos atrasados, la tasa de interés y el plazo se ilustran en el cronograma.
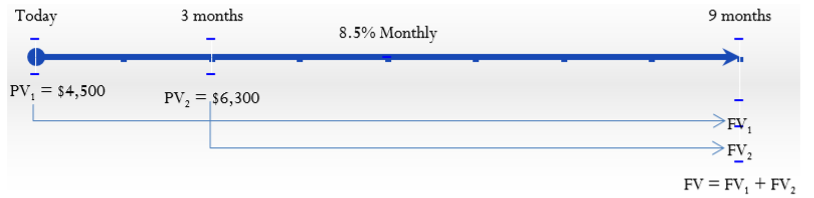
\(PV_1\)(hoy) = $4,500;\(PV_2\) (dentro de 3 meses) = $6,300;\(IY\) = 8.5%;\(CY\) = 12
Paso 2:
Fecha de vencimiento para todos = 9 meses a partir de hoy. Esta es tu fecha focal.
Cómo Llegarás
Paso 3:
Calcular la tasa de interés periódica aplicando la Fórmula 9.1.
Paso 4:
Para cada pago, calcule el número de periodos compuestos (\(N\)) aplicando la Fórmula 9.2.
Paso 5:
Para cada pago, calcule el valor de vencimiento (\(FV_1\)y\(FV_2\) aplicando la Fórmula 9.3.
Paso 6:
Calcular el pago total sumando los dos pagos, (\(FV_1\)y\(FV_2\), juntos.
Realizar
Paso 3:
\[i=\dfrac{8.5 \%}{12}=0.708 \overline{3} \%=0.00708 \overline{3} \nonumber \]
Paso 4:
El primer pago se mueve nueve meses en el futuro, o 9/12 de un año. \(N\)= 12 × 9/12 = 9.
El segundo pago se mueve seis meses en el futuro, o 6/12 de un año. \(N\)= 12 × 6/12 = 6.
Paso 5:
Primer pago:\(FV_{1}=\$ 4,500(1+0.00708 \overline{3})^{9}=\$ 4,795.138902\)
Segundo pago:\(FV_{2}=\$ 6,300(1+0.00708 \overline{3})^{6}=\$ 6,572.536425\)
Paso 6:
\[FV=\$ 4,795.138902+\$ 6,572.536425=\$ 11,367.68 \nonumber \]
Instrucciones de la calculadora
| Pago | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 9 | 8.5 | 4500 | 0 | Respuesta: -$ 4,795.138902 | 12 | 12 |
| 2 | 6 | \(\surd\) | 6300 | \(\surd\) | Respuesta: -$ 6.572.526425 | \(\surd\) | \(\surd\) |
Con intereses, los dos pagos suman $11,367.68. Se trata de los $10,800 del principal original más 567.68 dólares en intereses por realizar los pagos atrasados.
Tiene tres deudas con el mismo acreedor: $3,000 adeudados hoy, $2,500 adeudados en 2¼ años, y $4,250 adeudados en 3 años 11 meses. Al no poder cumplir con esta obligación, usted acuerda con su acreedor realizar dos pagos alternativos: $3,500 en nueve meses y un segundo pago vencido en dos años. Usted acuerda una tasa de interés de 9.84% compuesto mensual. ¿Cuál es el monto del segundo pago?
Solución
Determinar el monto del segundo pago que vence dos años a partir de hoy. Aplicar el concepto fundamental de valor temporal del dinero, moviendo todo el dinero de las corrientes de pago originales y propuestas a una fecha focal posicionada en el pago desconocido. Una vez que todo el dinero se traslade a esta fecha focal, aplicar el concepto fundamental de equivalencia, resolviendo para el pago desconocido, o\(x\).
Lo que ya sabes
Paso 1:
Con dos flujos de pago y múltiples montos, todos en fechas diferentes, visualice dos líneas de tiempo. Se conocen los montos de pago, la tasa de interés y las fechas de vencimiento para ambas corrientes de pago.
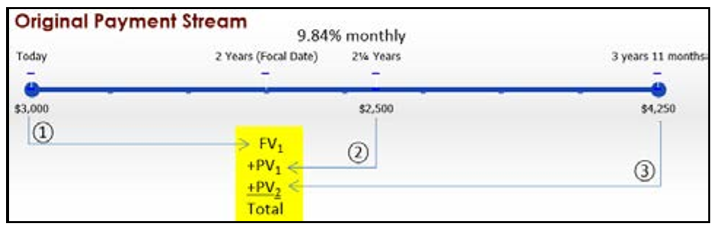
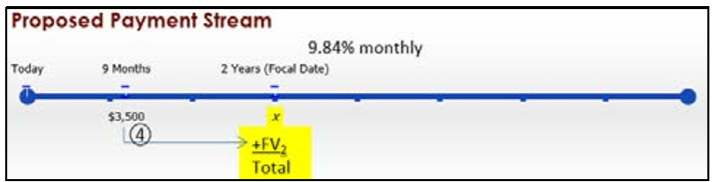
\(IY\)= 9.84%;\(CY\) = mensual = 12
Cómo Llegarás
Paso 2:
Se ha seleccionado una fecha focal de Year 2.
Paso 3:
Calcular la tasa de interés periódica aplicando la Fórmula 9.1.
Paso 4:
Para cada pago, calcule el número de periodos compuestos aplicando la Fórmula 9.2.
Paso 5:
Para cada pago, aplique la Fórmula 9.3. Tenga en cuenta que todos los pagos antes de la fecha focal de dos años requieren que calcule los valores futuros, mientras que todos los pagos posteriores a la fecha focal de dos años requieren que calcule los valores actuales.
Paso 6:
Establezca el valor del flujo de pago original igual al flujo de pago propuesto. Resolver para el pago desconocido,\(x\), usando álgebra.
\(FV_{1}+PV_{1}+PV_{2}=x+FV_{2}\)
Realizar
Paso 3:
\[i=\dfrac{9.84 \%}{12}=0.82 \% \text { or } 0.0082 \nonumber \]
Pasos 4 y 5:
Usando las referencias numéricos en un círculo de las líneas de tiempo:
①\(N = 12 × 2 = 24\);\(FV_1 = \$3,000(1 + 0.0082)^{24} = \$3,649.571607\)
②\(N= 12 × ¼ = 3\);\(\$2,500 = PV_1(1 + 0.0082)^3\);\(PV_{1}=\dfrac{\$ 2,500}{1.0082^{3}}=\$ 2,439.494983\)
③\(N=12 \times 1 \tfrac{11}{12}=23\);\(\$ 4,250=PV_{2}(1+0.0082)^{23}\);\(PV_{2}=\dfrac{\$ 4,250}{1.0082^{23}}=\$ 3,522.207915\)
④\(N=12 \times 1\tfrac{1}{4}=15\);\(FV_{2}=\$ 3,500(1+0.0082)^{15}=\$ 3,956.110749\)
Paso 6:
\ [\ begin {aligned}
\ $ 3,649.571607+\ $ 2,439.494983+\ $3,522.207915 &=x+\ $3,956.110749\
\\ $9,611.274505 &=x+\ $3,956.110749\
\ $5,655.16 &=x
\ end {alineado}\ nonumber\]
Instrucciones de la calculadora
| Cálculo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| ① | 24 | 9.84 | 3000 | 0 | Respuesta: -$ 3,649.571607 | 12 | 12 |
| ② | 3 | \(\surd\) | Respuesta: -$ 2.439.494983 | \(\surd\) | 2500 | \(\surd\) | \(\surd\) |
| ③ | 23 | \(\surd\) | Respuesta: -$ 3.522.207915 | \(\surd\) | 4250 | \(\surd\) | \(\surd\) |
| ④ | 15 | \(\surd\) | 3500 | \(\surd\) | Respuesta: -$ 3,956.110749 | \(\surd\) | \(\surd\) |
El segundo pago es de $5,655.16. Esto hace que los acuerdos originales y propuestos sean equivalentes entre sí.

Trabajar con Préstamos y Pagos
Los conceptos fundamentales de relación calidad-precio en el tiempo y equivalencia te ayudarán a entender mejor cómo operan los préstamos. Cuando se establece un préstamo, se establece el número de pagos y los montos de reembolso. Dado que el préstamo adquiere intereses a lo largo de la transacción, esto significa que los pagos futuros deben devolver tanto el principal como los intereses. En última instancia, todos los pagos de préstamos juntos necesitan reembolsar completamente al prestamista el monto total del principal.
Principio de Valor Presente para Préstamos
El principio de valor presente para los préstamos establece que el valor presente de todos los pagos de un préstamo es igual al principal que se tomó prestado. Como se ilustra en el cronograma, tomando todos los pagos futuros y eliminando los intereses, los pagos deben ascender al monto principal original en la fecha inicial del préstamo. La tasa de interés utilizada en este cálculo es la tasa de interés para el propio préstamo.
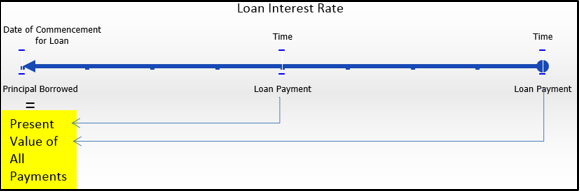
Esta relación se puede expresar de la siguiente manera:
\[\text{Principal Borrowed }=\text{ Present Value of All Payments}\nonumber \]
Cómo funciona
Cuando trabajas con préstamos, las variables desconocidas más comunes son el principal prestado o el monto o montos de cualquier pago desconocido. Sigue los mismos pasos que para los pagos equivalentes, discutidos anteriormente en esta sección.
Por ejemplo, supongamos que un préstamo requiere dos pagos iguales de $1,000 semestrales y quieres conocer el principal original del préstamo. La tasa de interés del préstamo es de 7.1% compuesto semestralmente.
Paso 1: Aquí se ilustra el tim eline.
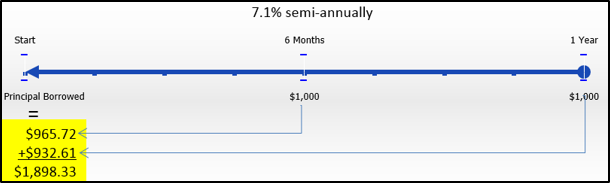
Paso 2: De acuerdo con el principio de valor presente para los préstamos, cuando devuelve los dos pagos a la fecha de inicio del préstamo (la fecha focal), entonces la suma de los valores actuales equivale a la cantidad inicial prestada.
Paso 3: El\(IY\) = 7.1% y\(CY\) = 2, por lo tanto\(i=7.1 \% / 2=3.55 \%\).
Paso 4: El primer pago tiene que volver al\(\dfrac{1}{2}\) año, o\(N=2 \times \dfrac{1}{2}=1\). El segundo pago tiene que regresar 1 año, o\(N=2 \times 1=2\).
Paso 5: Aplicando la Fórmula 9.3, para el primer pago\(\$ 1,000=PV(1+0.0355)^{1}\) o\(PV=\$ 965.717044\). Para el segundo pago,\(\$ 1,000=P V(1+0.0355)^{2}\) o\(PV=\$ 932.609410\).
Paso 6: La cantidad prestada es la suma de los dos valores presentes, o\(\$ 965.717044+\$ 932.609410=\$ 1,898.33\). Al 7.1% semestral, dos pagos de $1,000 semestrales amortizan un préstamo de $1,898.33.
Caminos hacia el éxito
Aún puedes usar los botones de valor de dinero en tiempo en tu calculadora para realizar cálculos que involucren variables desconocidas. Recordemos de la discusión álgebra en la Sección 2.4 que cualquier término algebraico consiste en un coeficiente tanto numérico como literal. Para mover una variable desconocida a través del tiempo, ingrese el coeficiente numérico de la variable en la calculadora y calcule su nuevo valor en la fecha focal. Este nuevo valor en su fecha focal debe entonces tener el coeficiente literal escrito después de él antes de continuar con operaciones posteriores.
Por ejemplo, si desea realizar un cálculo de valor presente sobre un valor futuro de\(2y\), ingrese el coeficiente numérico “2” como su\(FV\) y calcule el\(PV\). Supongamos que el\(PV\) es 1.634. El coeficiente literal no ha desaparecido. Simplemente no pudiste ingresar la letra en la calculadora. Por lo tanto, copiando el coeficiente literal al valor presente tú mismo, eso lo ves\(PV = 1.634y\). Ejemplo\(\PageIndex{3}\) aplica este concepto.
- El principal de un préstamo es de $10,000 y se requieren dos pagos. Si el primer pago es de $5,000, ¿qué estado de cuenta podrías hacer sobre el segundo pago?
- Considera dos préstamos. El primero requiere cuatro pagos trimestrales de $2,500. El segundo préstamo requiere cuatro pagos mensuales de $2,500. Asumiendo tasas de interés iguales, ¿qué declaración podría hacer sobre los principales de estos dos préstamos?
- Contestar
-
- El principal es inferior a $8,000 ya que los cuatro pagos deben tener los intereses eliminados.
- El segundo pago es superior a $5,000 ya que debe devolver los intereses así como el capital restante.
- El principal del segundo préstamo es mayor ya que los pagos se realizan solo cuatro meses después, por lo que implican relativamente pocos intereses. Los pagos del primer préstamo se extienden por un año, por lo que requiere la eliminación de mayores sumas de interés para llegar al principal
Un préstamo de $24,000 al 7% compuesto semestral requiere tres pagos a 1½ años, 3 años y 4 años. El primer pago es de $3,000 y el segundo es tres veces más grande que el pago final. Calcular los valores del segundo y tercer pago del préstamo.
Solución
Encuentra el monto del segundo y tercer pago. Dado que el segundo pago es tres veces el tamaño del tercer pago, resolver para el tercer pago, o\(x\), y luego calcular el segundo pago después.
Lo que ya sabes
Paso 1:
Se conocen el principal, los montos de pago, la tasa de interés y las fechas, como se indica en el cronograma.
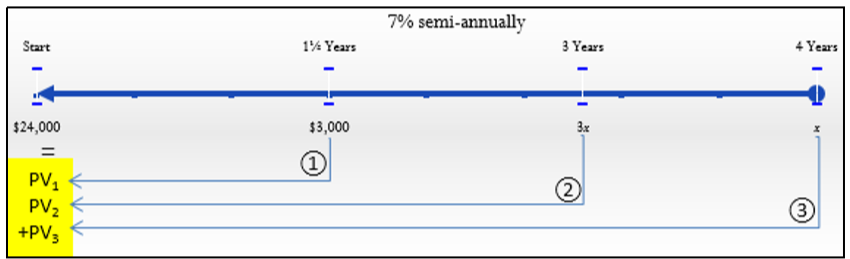
\(IY\)= 7%;\(CY\) = 2 Nota: Si el pago final es x y el segundo pago es tres veces mayor, entonces es igual\(3x\).
Cómo Llegarás
Paso 2:
La fecha focal es el inicio del préstamo.
Paso 3:
Calcular la tasa de interés periódica aplicando la Fórmula 9.1.
Paso 4:
Para cada pago, calcule el número de periodos compuestos aplicando la Fórmula 9.2.
Paso 5:
Por cada pago aplica la Fórmula 9.3.
Paso 6:
Utilizando el principio de valor presente para los préstamos, equiparar los pagos y el principal, luego resolver para la variable desconocida\(x\).
\(\text { Principal }=PV_{1}+PV_{2}+PV_{3}\)
Una vez que lo sepas\(x\), calcula el tamaño del segundo pago =\(3x\).
Realizar
Paso 3:
\[i=\dfrac{7 \%}{2}=3.5 \%=0.035 \nonumber \]
Pasos 4 y 5:
Usando las referencias de números con un círculo en la línea de tiempo:
①\(N=2 \times 11 / 2=3 ; \$ 3,000=PV_{1}(1+0.035)^{3} ; PV_{1}=\dfrac{\$ 3,000}{1.035^{3}}=\$ 2,705.828117\)
②\(N=2 \times 3=6 ; 3 x=PV_{2}(1+0.035)^{6} ; PV_{2}=\dfrac{3 x}{1.035^{6}}=2.440501 x\)
③\(N=2 \times 4=8 ; x=PV_{3}(1+0.035)^{8} ; PV_{3}=\dfrac{x}{1.035^{8}}=0.759411 x\)
Paso 6:
\ [\ begin {alineado}
\ $24,000 &=\ $ 2.705.828117+2.440501 x+0.759411 x\\
\ $24,000 &=\ $ 2.705.828117+3.199913 x\\
\ $21,294.17188 &=3.199913 x\\
\ $6,654.61 &=x
\ end {alineado}\ nonumber\]
Resolviendo para el\(3x\) pago:\(3($6,654.61) = \$19,963.83\)
Instrucciones de la calculadora
| Cálculo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| ① | 3 | 7 | Respuesta: $2,705.828117 | 0 | -3000 | 2 | 2 |
| ② | 6 | \(\surd\) | Respuesta: 2,440501 | \(\surd\) | 2500 | \(\surd\) | \(\surd\) |
| ③ | 8 | \(\surd\) | Respuesta: 0,759411 | \(\surd\) | -1 | \(\surd\) | \(\surd\) |
El segundo pago, ubicado a tres años del inicio del préstamo, es de 19.963.83 dólares, lo que es tres veces el tamaño del pago final de $6,654.61 un año después.


